巧用“1”的逆代换求解最值问题

张之阅

(江苏省扬州中学高一(13)班，225009)

类型1整式和与分式和在条件与结论中搭配

求解此类问题的关键是观察分式中分母的和与整式的关系,合理配凑.

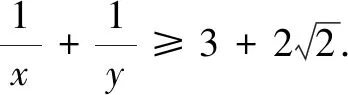
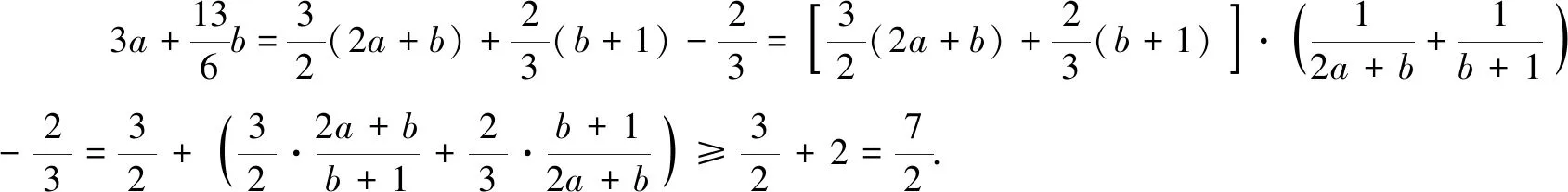
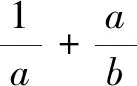
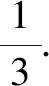
评注解法5充分利用椭圆的参数方程，将所有点的坐标都“三角化”.除了开始利用椭圆的定义研究两个三角形的周长,再利用分割法和等积法将r1-r2表示为三角函数的形式.在后面的变形求解过程中,同角三角函数关系、两角和差公式、二倍角公式、和差化积公式、万能公式等诸多三角公式轮番上阵,令人目不暇接.本题的计算量之大,三角恒等变换能力要求之高,非同一般.

上面对一道椭圆联赛试题运用了5种方法进行解答.5种解法各具特色、精彩纷呈,其中前4种方法凸显了“将几何问题转化为代数问题,通过代数运算研究几何图形性质,图形问题代数化”的数学本质,解法5则侧重了三角恒等变换的运用.比较而言,我们更推崇前两种方法,即解法1和解法2,尤以解法1为主,后面三种方法作为辅助,仅供大家开阔思路参考.

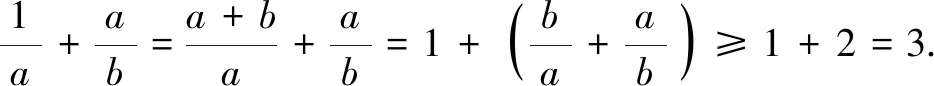
评注观察整式与分式分母的关系,是“1”的逆代换的前提,有时部分逆代换,有时整体逆代换,但是目标是化成齐次式,这正是数学思维灵活变通的体现.

类型2条件中整式和分式混合

此类问题的解法是将已知条件中整式和分式部分分别看作两个整体,适当重组,巧妙凑“1”.

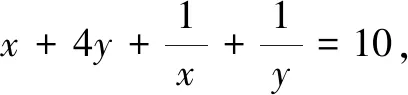
评注求解此类问题的关键在于抓住已知条件的结构特点,合理挖掘隐藏条件,配凑出“1”的恒等式,解题思路既合理自然,又富有创意,解题过程让人产生一种拨开云雾见月明的领悟.

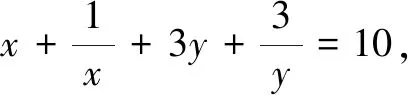
(参考答案:[2,8])

类型3在不等式条件下求函数的最值

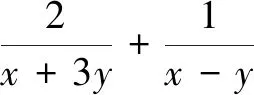
评注本解法利用不等式构造常数“1”进行逆代换,方便了放缩法构造齐次式解题.

评注利用分母的和为常数配凑,也是化为齐次式的一个手段.本题中的”1”逆代换为x+(1-x),技巧性比较强,但与二元参数本质上是相同的.

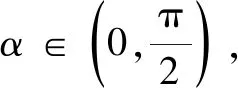
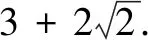
类型4条件和结论之间关系不明显

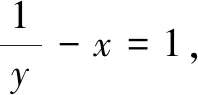
分析可利用减元思想显神效,或者将“1”逆代换二次,运用基本不等式解题.

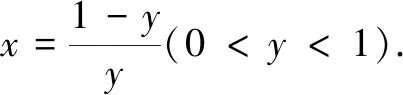
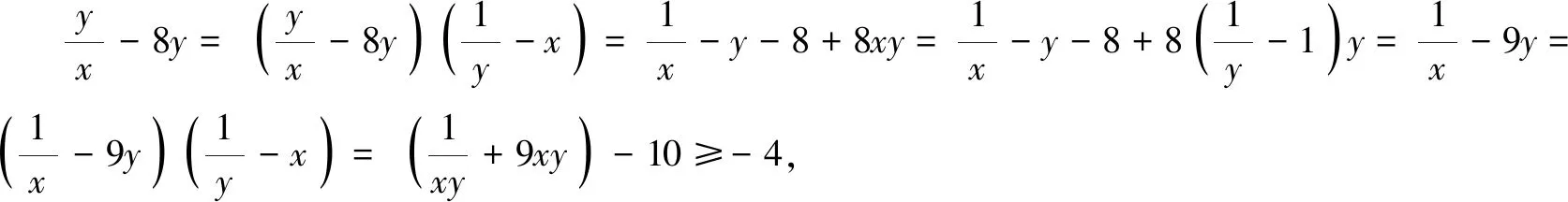
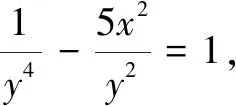
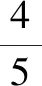
评注减元降维思想是处理多元问题的基本思路,“1”的逆代换只是解决问题的一种方法,虽然简洁,但不是万能的.

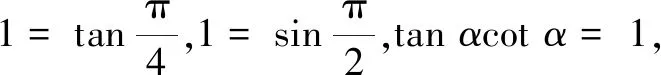
(指导老师:成晓燕)