“取道”空间图形建模 助力核心素养发展 *——例谈立体几何中的隐形正方体

孙风建 管慧慧

(江苏省南京师范大学附属中学,210003)

正方体是学生最熟悉的简单几何体,它不但包含了立体几何中研究的点、线、面的位置关系,更因其完美的对称性具备其他图形难以企及的优越性质.如果能挖掘题设条件,展开联想,巧妙地将隐形正方体显性化,使其特性即可得到充分利用,问题常能变得豁然开朗.构建正方体模型,不仅是一种解题方法,其中更蕴含丰富的数学思想,更是数学建模能力的有力体现,在立体几何领域有着极其重要的地位.本文示例说明其常见类型.

一、构建几何体外接隐形正方体模型,求解截面最值问题

截面问题是立体几何作图的一大难点,截面的最值问题更难.截面问题即共面问题,在立体几何中将一个平面放大的常用方式有两种:一是将其中一条或两条直线延伸,二是过平面的一点,作平面内某一条直线的平行线.另外，作截面涉及到直线与平面的交点,这通常转化为线与线的交点,因此截面问题可综合考察线面位置关系.

例1如图1,已知四面体ABCD的各条棱长均等于4,E,F分别是棱AD,BC的中点.若用一个与直线EF垂直,且与四面体的每一个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积的最大值为______.

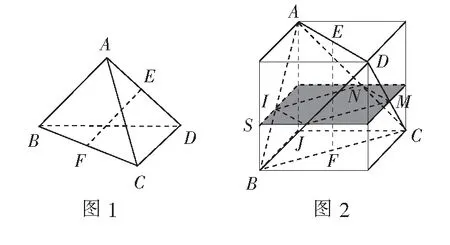
建模分析此题求解的关键是如何寻找与直线EF垂直的平面α.其次是当平面α平行移动时截面如何变化.这两个问题对学生来说都有很大的挑战.但由正四面体与正方体具有的天然关系,把正四面体放置到正方体中,这两个问题就易于解决.

解如图2,将正四面体放置到正方体中,则易知平行于底面的平面α与直线EF垂直.记平面α与正四面体的各条边的交点分别为I,J,M,N.根据平行平面的性质,得IN∥BC,JM∥BC,IJ∥AD,MN∥AD,所以IN∥JM,IJ∥MN,四边形IJMN为平行四边形.又AD⊥BC,所以四边形IJMN为矩形.

评注此解法中的正方体起到很好的衬托作用.借助于正方体,能非常直观地看到与EF垂直的平面,以及平面α变化时截面变化过程中保持矩形的形状不变.

二、构建隐形正方体内(外)切球的一般模型

正方体的内切球或者外接球是立体几何的经典模型,对培养学生空间想象能力、建构模型能力是非常有帮助的.正方体的内切球或外接球又因其直观、简单,学生大都易掌握和熟悉.

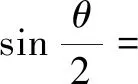
建模分析AB,CD的长度是变化的,异面直线AB,CD所成的角以及“距离”也是变化的,这些量如何确定四面体ABCD是解决问题的第一步,也是最为关键的一步;其次,确定AB,CD的位置关系后,再计算异面直线所成角的半角.由此构造一个正方体,使小球为正方体的内切球,大球为正方体的外接球,这样确定AB与CD的位置后,方便计算异面直线所成角的半角.

解首先解决第一个问题.直观感知是AB,CD的长度以及它们的所成角和距离(公垂线段)都是独立的量,当AB,CD最长,公垂线段最长,AB,CD所成角为90°时,四面体ABCD的体积最大.但是事实是不是这样呢?需要先论证如下的引理.

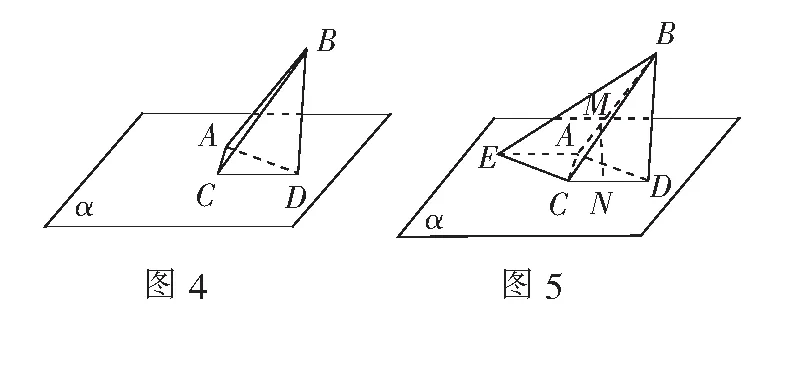
证明如图5,过点C,A分别作AD,CD的平行线交于点E,则四边形ECDA为平行四边形,异面直线AB与CD所成角为∠EAB或其的补角,且S∆ACD=S∆ACE.

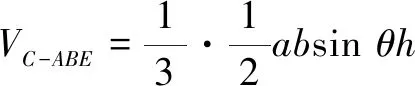
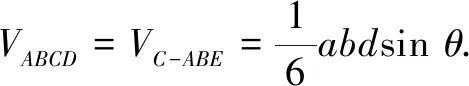
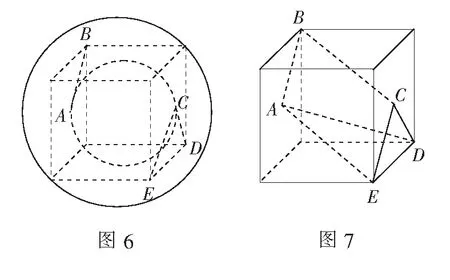
如图7,A,C为正方体对面的中心,显然AB与CD满足条件,在正方体中显然有AB∥EC,且AB=EC.因此，四边形BAEC为平行四边形,从而AE∥BC.故异面直线AD与BC的所成的角,即为AD与AE的夹角或其补角θ.

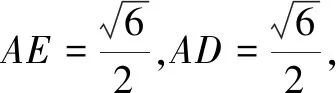
评注在教学过程中,很多学生获得了最终结果.但在求VABCD的最大值时,大部分学生仅凭借直观想象后建立模型；有的学生用空间向量处理.对于空间问题,直觉思维或空间想象力非常重要,应鼓励学生先大胆猜想,然后凭借严密的逻辑推理进一步论证,从而实现对问题更深层次的认知.只有这样的思维锻炼,才能灵活进行空间几何体的建模.

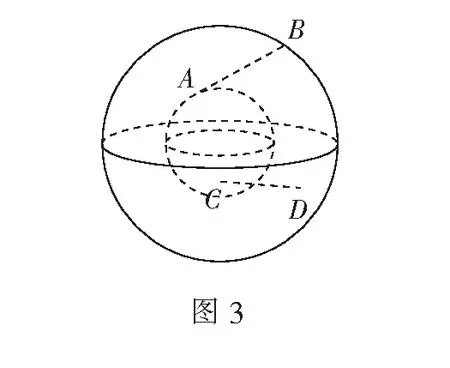
三、构建球面几何中的隐形正方体模型

球面几何是几何学的一个重要分支,在航海、航空、卫星定位、镜面成像等方面都有广泛的应用.另一方面,球面几何不是欧氏几何,而是一个重要的非欧几何模型,对拓展学生的视野,让学生感知自然界中存在丰富多彩的数学模型大有益处,不仅能增强学生的好奇心,也可激发学生学习数学的热情.

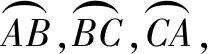
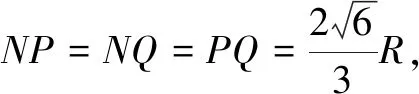
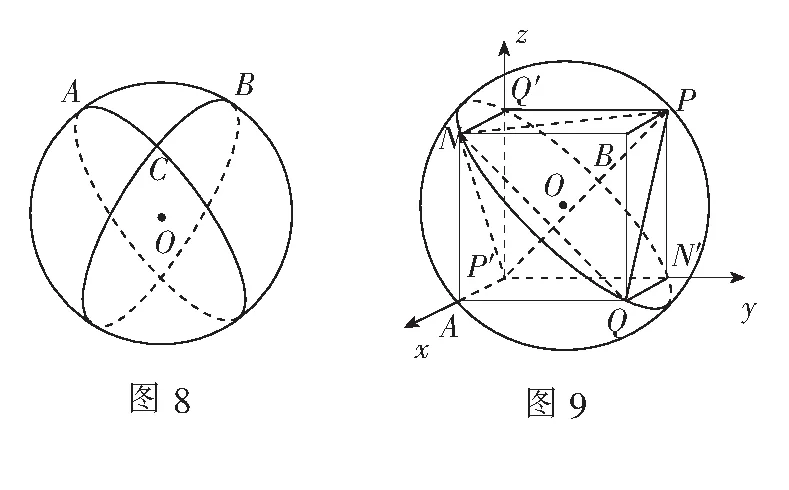
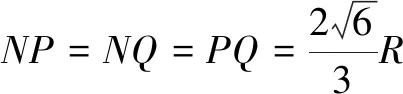
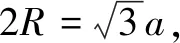
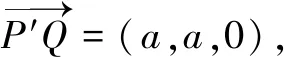
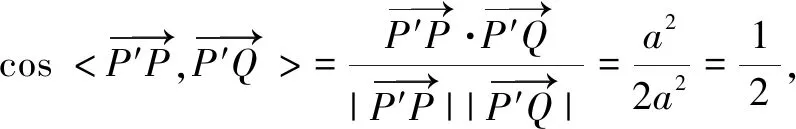
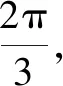
评注本题是一道球面几何文化题,对学生来说非常陌生,学生通过阅读获得球面三角形的面积公式后,面临的难点就是怎么计算球面三角形的“内角”.根据定义,必须知道球面三角形中任意两个点所在大圆的平面,不仅要计算二面角,还要正确判断是锐角还是钝角.因此没有确定的、清晰的位置关系,问题将难以解决,而根据三点的长度关系构造正方体,有效化解了上述难点,方便了解题.

三、结束语

涉及隐形正方体的问题背景非常丰富,常涉及空间几何的体积、长度、距离、异面直线所成角、解三角形等知识,对考生的逻辑推理、运算、建模等综合应用能力要求较高. 用隐形正方体建模求解,我们可以先通过直观想象、数学抽象认识问题背景,获得隐形正方体的关键模型要素,再通过类比、联想、特殊化、一般化等推理活动理顺建模思路、找到研究方法,也可通过单元式主题探究形成整体思维,最终帮助学生实现 “四基”、“四能”向数学核心素养的发展[1].