点到直线距离公式的细化及应用

贺德光

(湖南省衡东县第一中学,421400)

若把A2+B2≠0时平面直角坐标系中的向量n=(A,B) 叫做直线l:Ax+By+C=0的一个“法向量”,那么我们就可按文[1]的思路方法将点到直线的距离公式进行细化.

=Ax0+By0-Ax1-By1.

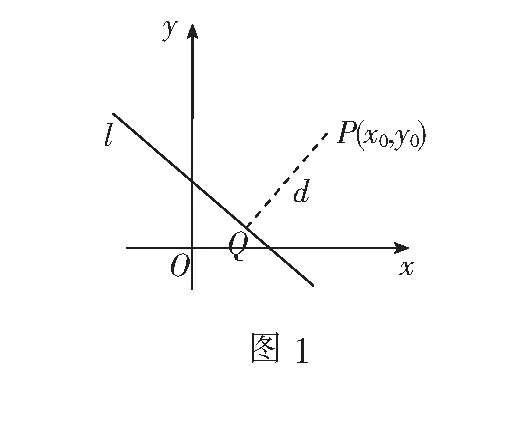
综上，可得

评注以上点到直线的距离公式之细化结论,在没有学习“平面直角坐标系中二元一次不等式表示平面区域”的情况下能起到积极的作用.例如下述高考题第(2)问,就可以用该结论1来解决.

(1)求C1,C2的方程;

(2)过F1作C1的不垂直于y轴的弦AB,M为AB的中点.当直线OM与C2交于P,Q两点时,求四边形APBQ面积的最小值.

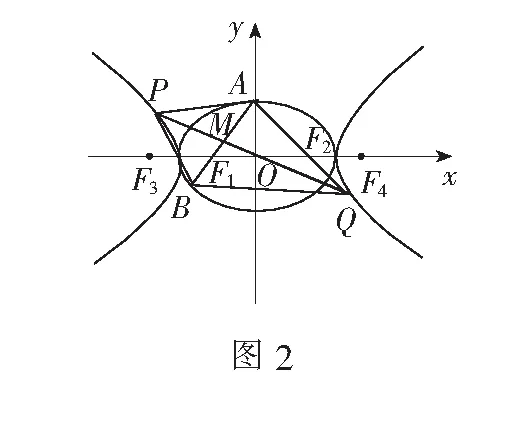
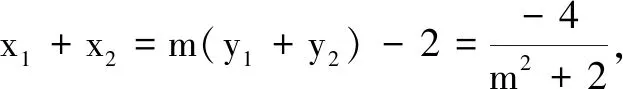
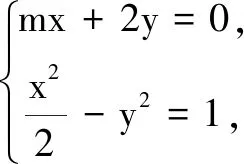
又xi=myi-1(i=1,2),故|mx1+2y1|+|mx2+2y2|=mx1+2y1-(mx2+2y2)=(m2+2)(y1-y2),于是

从而四边形APBQ的面积

而0<2-m2≤2,故当m=0时,四边形APBQ的面积取最小值2.

评注借鉴前面点到直线距离公式的细化过程,结合例1(2)的解答过程,不难推证得如下结论.

结论2若点P(x1,y1)与Q(x2,y2)位于直线l:Ax+By+C=0(A2+B2≠0)的两侧,则(Ax1+By1+C)(Ax2+By2+C)<0.

例2在平面直角坐标系中,已知直线l过点P(-1,2),且与以A(-2,-3),B(3,0)为端点的线段有公共点,求直线l斜率的取值范围.

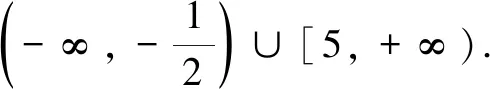
教材的资源是无穷无尽、丰富多彩的.以上结果表明,只要我们静下心来细心研究,会有许多数学的奥秘被挖掘出来,我们的视野也会因此而变得更加广阔、深远.