先猜后证巧转化 合情推理妙解题

赵泽民

(甘肃省永昌县第一高级中学，737200)

从具体问题出发,通过分析、比较、归纳进而提出合理的猜想是合情推理的基本思想.在数学解题的过程中运用合情推理常常能为解题提供思路和方向,通过“先猜后证”可以突破一些数学问题的难点,优化解题过程.本文通过先猜后证的方法在圆锥曲线、导数综合问题、数列中的运用,构建不同的解题思路，巧妙解决2020年模考题和高考题,以期抛砖引玉.

一、先猜后证在圆锥曲线中的应用

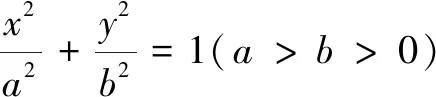
(1)求椭圆的标准方程;

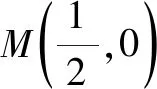
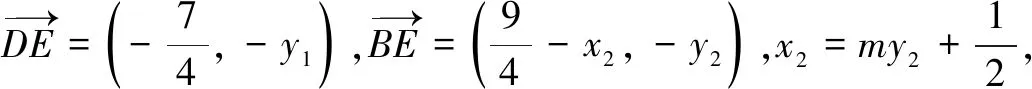
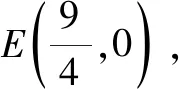
二、先猜后证在导数综合题中的应用

例2已知函数f(x)=ex.

(1)求曲线y=f(x)在点(1,f(1))处的切线方程;

解(1)y=ex.(过程略)

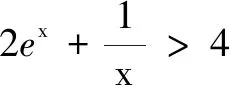
综上,整数k的最大值为2.

评注本题涉及零点不可解问题,正面解答有一定难度,运用先猜后证思路可绕过零点值合理猜想出整数k的最大值,再借助ex>x+1(x>0)给出严谨的证明,优化了解题过程,降低了思维难度.无独有偶,2020年新高考全国I卷第21题用先猜后证也可以巧妙解答,下面来欣赏一下.

例3(2020年全国高考题)已知函数

f(x)=aex-1-lnx+lna.

(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

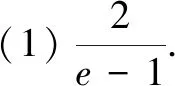
(2)依题意,有f(1)≥1,即a+lna≥1.注意函数g(x)=x+lnx在(0,+∞)单调增,且g(1)=1,所以a+lna≥1的解为a≥1.猜想a的取值范围为a≥1,下面给出证明.

因为ex≥x+1(x∈R)等价于lnx≤x-1(x>0),所以当a≥1时,f(x)≥ex-1-lnx≥(x-1)+1-lnx=[(x-1)-lnx]+1≥1.

综上,a的取值范围为a≥1.

三、先猜后证在数列问题中的应用

例4设数列{an}的前n项和为Sn,满足Sn=2nan+1-3n2-4n,n∈N*,且S3=15.

(1)求a1,a2,a3的值;

(2)求数列{an}的通项公式.

解(1)a1=3,a2=5,a3=7.(过程略)

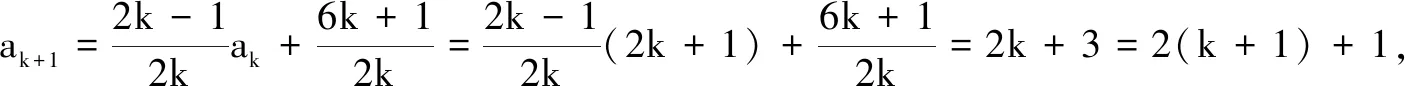
综上,{an}的通项公式为an=2n+1.

评注在数列问题中,若直接求通项公式受阻,可通过合情推理归纳猜想出结论,然后利用数学归纳法给予证明.以下展示的2020年全国Ⅲ卷数列问题就体现了这一点.

例5(2020年全国高考题)设数列{an}满足a1=3,an+1=3an-4n.

(1)计算a2,a3,猜想{an}的通项公式并加以证明;

(2)求数列{2nan}的前n项和Sn.

解(1)由题意易得a2=5,a3=7.故猜

想an=2n+1.

下面给出证明:当n=1,2,3时,结论显然成立.假设n=k时猜想成立,即ak=2k+1,则当n=k+1时,ak+1=3ak-4k=3(2k+1)-4k=2(k+1)+1,猜想也成立.

综上,an=2n+1(n∈N*).

(2)令bn=2nan=(2n+1)2n,则Sn=3×2+5×22+…+(2n-1)2n-1+(2n+1)2n,2Sn=3×22+5×23+…+(2n-1)2n+(2n+1)2n+1.两式相减,得-Sn=6+2(22+23+…+2n)-(2n+1)2n+1,易得Sn=(2n-1)2n+1+2.

总之,先猜后证既是突破难点问题的思维方法,又是优化解题过程的一种策略.它能有效突破思维定势的束缚,合理、巧妙地对数学问题进行转化,有助于提高解题能力,提升学生的逻辑推理素养.