水下爆炸作用下近岸场地动态响应数值模拟

尹训强， 吕硕硕， 王桂萱

(大连大学建筑工程学院， 大连 116622)

水下爆炸对于近岸工程结构及周围既有建筑的安全具有重大的影响。通常情况下，水下爆炸会比空气中爆炸产生更强的地震效应，对建筑结构造成更大的破坏。这主要是由两个因素导致的，其一是水下爆炸所产生的冲击波峰值压力要大于空气中爆炸，其二是水下岩土处于过饱和状态。因此，需通过对炸药在水下爆炸现象的数值模拟，深入研究水下爆炸冲击作用下冲击波的传播特性以及近岸场地的动态响应变化规律，为近岸结构安全和防护工程设计提供可靠的数据支撑。

李麒等[1]利用Python语言对ABAQUS进行二次开发，开展大坝损伤识别方法研究；吕林梅等[2]建立了以损伤面积率作为指标的大坝损伤评价方法；张守旸等[3]通过数值模拟的方法证明了聚脲涂层对结构的抗爆性能有一定程度的提高。闫秋实等[4]通过数值软件对高桩码头抗爆性进行研究，得到了在确定爆炸深度下的对应安全范围。

目前水下爆炸的研究多集中在大坝等建筑物上[5]，而对于码头、防波堤以及周边既有建筑物等的影响研究还比较少[6-7]，也未曾有学者探讨爆源的位置对近岸场地是否存在影响。现针对不同装药量的爆源、不同水下爆炸位置，开展水下爆炸冲击波对近岸场地的影响分析，得到爆炸冲击作用下冲击波的传播特性以及近岸场地动态响应的变化规律。

1 水下爆炸下近岸场地分析模型

由于水下爆炸的复杂性，很难采用理论和试验研究的方法。随着计算机技术的不断发展，数值模拟的方法具有成本低、可操作性强的优点，被广泛应用于水下爆炸的研究中。主要采用数值模拟的研究方法，通过ANSYS/LS-DYNA软件建立符合实际情况的水下爆炸流固耦合模型，分析不同炸药量、不同起爆位置对近岸结构的影响。

1.1 有限元模型

依据某近岸场地地质参数、水文资料等建立有限元模型，爆源起爆位置位于某海区中央洪池处，洪池直径200 m，设计底高程-45 m，如图1所示。

近岸场地动力响应数值分析模型如图2所示，其中，水、空气、炸药采用欧拉建模，护岸结构、防波堤以及场地土则采用拉格朗日建模，单元采用多物质任意拉格朗日欧拉(arbitrary Lagrangian Eulerian，ALE)算法[8]。采用Z方向的对称建模，并施加对称约束，其他截断边界均施加无反射边界。

图1 近岸场地布设剖面图Fig.1 Profile of site layout near shore

图2 近岸场地动力响应数值分析模型Fig.2 Numerical analysis model of dynamic response of nearshore site

1.2 材料参数选取

在LS-DYNA中模拟选取的炸药为三硝基甲苯(trinitrotoluene，TNT)高能炸药，关键字为*MAT- HIGH-EXPLOSIVE-BURN，对炸药采用的是Jones- Wilkins-Lee(JWL)状态方程，此状态方程[9-10]表达式为

(1)

式(1)中：ω、A、B、R1、R2为描述炸药特性的常数；V为相对体积；P为压力；E为单位体积内能。此方程能很好地描述高能炸药，确定炸药的爆轰压力。

空气材料采用的卡片是MAT_NULL模型，采用的状态方程是线性多项式方程，此状态方程为

P=C0+C1μ+C2μ2+C3μ3+

(C4+C5μ+C6μ2)E

(2)

式(2)中：C0、C1、C2、C3、C4、C5、C6为常数。当体积变化率μ<0 时，C2μ2=0，C6μ2=0，μ=1/V-1。

水体所用的模型是 *MAT_NULL卡片模型，状态方程所用的是 *EOS_GRUNEISEN状态方程，此状态方程所定义的压缩材料压力为

(γ0+aμ)E

(3)

式(3)中：ρ0为初始密度；C为冲击波速度us与质点速度up曲线的截距；γ0为Gruneisen系数；a为对γ0的一阶体积修正；S1、S2、S3为us-up曲线斜率的系数。压缩状态由相对体积定义为

(4)

质点速度表达式为

(5)

护岸及防波堤混凝土部分，选取材料为 *MAT_ BRITTLE_DAMAGE。基岩体选取的材料为 MAT003号 *MAT_PLASTIC_KINEMATIC。

2 水中冲击波传播特性

为了研究近岸场地水下爆炸所产生冲击波的传播特性，建立了近岸场地水中起爆与水底起爆两个模型，并将其数据进行对比分析。水下爆炸仿真模型的示意图如图3所示。

图4为500 kg炸药条件下水中起爆典型时刻冲击波压力分布图。可以看出，药包爆炸，产生爆轰压力，其压力呈球形向周围扩散，爆炸产生的冲击波传至水面，一部分冲击波受自由水面影响，产生波的反射，在水面下产生与入射波方向相反的稀疏波；另一部分以透射波的形式透过水面传播到空气介质[11]。当冲击波传至水底时，一部分冲击波由于水底结构的波阻抗大于水介质，会出现波的反射，产生反射冲击波，并且该冲击波的性质与入射波相同。在反射波与入射波的共同作用下，水底结构附近的压力会再次上升。随着反射冲击波的不断传播，稀疏波会因为反向冲击波与水中气泡发生相互作用而产生，气穴效应也随之产生；另一部分则以透射波的形式传到水底结构中。

图3 水中水底起爆示意图Fig.3 Schematic diagram of underwater explosion

图4 500 kg炸药条件水中起爆典型时刻冲击波压力图Fig.4 Pressure diagram of shock wave at typical time of underwater detonation under 500 kg explosive condition

为了更好地研究水下爆炸冲击波在水中的传播特性，沿垂直水底向下方向距爆源5、10、15、20、25 m设置4个观测点，观察其冲击波压力波形图变化(图5)。

图5 沿垂直水底向下离爆源不同距离处冲击压力波形图Fig.5 Waveform diagram of shock pressure at different distances from the explosion source along the vertical bottom

从图5中可以看出，监测点在很短时间内突然跃升到峰值压力，与经验公式描述结果基本相同。并且，随着监测点远离爆源，炮轰压力不断减小。但其与经验公式指数衰减又存在一定差别，爆炸冲击波传到水底岩石面处，会产生波的反射，形成反射波，其性质与入射波相同。从而，造成冲击波压力波形图出现多个峰值现象。并且，在冲击波传播过程中，监测点会出现压力值为负的情况，这是由于稀疏波的作用使得该点出现气穴效应导致的。

图6为500 kg炸药条件下水底起爆典型时刻冲击波压力分布图，冲击波传播方式与水中起爆大致相同，其中一部分以球状向四周扩散，当冲击波传至水面时会发生波的反射现象，在水面下方产生与入射波方向相反的稀疏波。由于爆炸点在水底，另一部分冲击波则会在接触底部岩石形成反射冲击波(岩石的波阻抗大于水)和透射波。反射波会使

图6 500 kg炸药下水底起爆典型时刻冲击波压力分布图Fig.6 Pressure distribution of shock wave at typical time of underwater initiation with 500 kg explosive

得水底结构附近的压力会再次上升。透射波则在底部岩石中传播并快速衰减。

为了更好地研究水下爆炸冲击波在水中的传播特性，沿垂直水底向上方向距爆源5、10、25 m设置3个观测点，观察其冲击波压力波形图变化(图7)。

从图7中可以看出，传播特性与水中起爆的变化规律基本一致，突然跃升到峰值压力，且随着监测点远离爆源，炮轰压力不断减小。但也存在少许不同，由于水底起爆的原因，与水中起爆相比，第一次波峰与第二次波峰出现的时间间隔较短。通过观察不难发现，随着监测点距离的增大，二次波峰的值逐渐减小。

图7 沿垂直水底向上离爆源不同距离处的冲击压力波形Fig.7 The shock pressure waveform at different distances from the explosion source along the vertical bottom

3 水下爆炸下近岸场地响应分析

为了研究不同炸药量以及不同起爆位置对近岸结构的影响，建立不同炸药当量(200 kg与500 kg)、不同水下爆炸位置工况条件(4个工况)下的爆炸数值模拟。具体工况如表1所示。

表1 水下爆炸工况表Table 1 Working table of underwater explosion

直立护岸和防波堤都是混凝土结构，混凝土等脆性材料具有很强的压缩性能和很弱的拉伸性能。因此，第一强度理论可以作为衡量混凝土结构是否安全的评判标准。通过对比结构第一主应力与混凝土抗拉极限值的大小关系，确定结构是否安全。当混凝土抗拉极限大于其第一主应力时，即可认为结构安全，反之，可认为混凝土已损坏，存在安全隐患。图8、图9显示了垂直护岸和防波堤的第一主应力在最大时刻的应力分布。

由图8、图9可知，4种工况下，直立护岸与防波堤的第一主应力最大值分别为0.84 MPa和0.72 MPa，均小于混凝土抗拉强度极限值；各工况下，防波堤与直立护岸的第一主应力最大值出现在水位以下近岸结构与水底岩石交界处。并且，水面以下迎水面部分的第一主应力大于水面以上，其原因在于水面以下部分受到水中爆炸冲击波作用，因此，在结构设计过程中需要对结构与底部岩石部分进行重点关注；通过对比不难看出，同一爆源深度情况下，炸药量越大，受到爆炸荷载影响，结构的最大应力值越大；在不同爆源深度下，水中爆炸对结构产生的第一主应力大于水下爆炸。

图10、图11所示为各工况条件下直立护岸侧的X向和Y向振动速度衰减曲线。可以看出，各工况条件下两方向的振动速度在近距离100 m范围内，速度衰减很快，在中远距离，随着距离直立护岸岸边的距离增大，其衰减速度有所趋缓，但振动速度依然很小。从各工况的对比来看，工况1条件下，直立护岸边的振动速度最大，X向和Y向振动速度分别为1.646 cm/s 和1.931 cm/s；而200 kg装药条件下水中爆炸也要比水底爆炸的产生的振动速度大，X向和Y向振动速度分别为1.348 cm/s和1.672 cm/s。并且，垂直Y向的振动速度要比水平X向的振动速度要大，这是由于水中爆炸作用于水底导致地震动与水冲击波的叠加，在直立护岸岸边处的振动速度最大发生在工况1条件下，最大值为1.931 cm/s。总体来看，水中爆炸工况要比水底爆炸工况对近岸场地产生的振动要大，这主要是水底爆炸时，爆炸点到直立护岸场地的距离要比水中爆炸要大，另一方面，水底爆炸在岩土介质中所传播能量要比水中爆炸时要大，但由于岩土介质中所施加的阻尼会快速耗能，从而导致该工况下直立护岸场地的响应要小一些。

图9 防波堤第一主应力最大值时刻应力分布图Fig.9 Stress distribution diagram of breakwater at the moment of maximum first principal stress

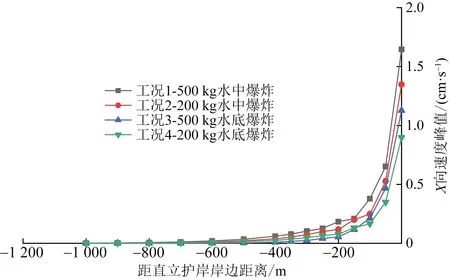
图10 直立护岸侧的X向振动速度衰减曲线Fig.10 X-direction vibration velocity attenuation curve on the side of vertical revetment

图11 直立护岸侧的Y向振动速度衰减曲线Fig.11 Y-direction vibration velocity attenuation curve of vertical revetment

4 结论

(1)爆炸冲击波的传播会受到边界面的影响。当冲击波传至水面时，水介质的密度和波阻抗远大于空气介质，在稀疏波产生的同时，近水面的压力会迅速下降，并降为负压值，产生气穴现象；冲击波传到水底岩石面处，会产生波的反射，形成反射波，其性质与入射波相同。从而，造成冲击波压力波形图出现多个峰值现象。

(2)与水中爆炸不同的是，水下爆炸由于下方岩土层的缘故，炮轰压力在下方岩土中的传播很快衰减，只在上方的水中则形成明显的球状扩散面。

(3)防波堤与直立护岸由于受水中爆炸冲击波作用的第一主应力最大值出现在水位以下的迎水面；同一爆源深度，炸药量越大，受到爆炸荷载影响，结构的最大应力值越大；在不同爆源深度下，水中爆炸对结构产生的第一主应力大于水下爆炸。

(4)当冲击波传至近岸结构处时，各工况下两方向振动速度在近距离100 m范围内迅速衰减，随着距离增大，其衰减速度有所趋缓；在相同工况下，垂直Y向的振动速度要比水平X向的振动速度要大；水中爆炸工况要比水底爆炸工况对近岸场地产生的振动要大；综合结构第一主应力以及X、Y方向的振动速度可以发现，炸药的起爆位置对近岸结构的安全有很大影响，水中起爆对近岸结构产生的冲击要大于水底起爆。