基于改进麻雀搜索算法-核极限学习机耦合算法的滑坡位移预测模型

马飞燕， 李向新

(昆明理工大学国土资源工程学院， 昆明 650093)

滑坡是一种由于自然环境变化或人类活动改变了边坡平衡状态后引起的地质现象。突发性的山体滑坡会造成巨大的生命和财产损失[1]。由此，对滑坡变形进行预测预警[2-3]越来越重要，多年来，研究人员将滑坡预测模型分为物理模型和数据驱动模型两大类[4]。

数据驱动模型相较物理模型强调根据以往的实测数据建立相关的数学模型进行预测。在影响滑坡稳定性的因素众多[5]，滑坡变形的物理机理比较复杂的情况下，数据驱动模型有着较好的预测精度。而随着计算机技术的发展，以神经网络模型[6]、支持向量机模型[7]、极限学习机模型[8]为代表的数学模型，由于对类似复杂条件下的滑坡体变形这样的非线性复杂系统行为[9]预测方面有着较好的准确性，逐渐成为数据驱动滑坡预测的研究热点。支持向量机和最新发展起来的极限学习机则克服了传统神经网络模型易造成局部最优的缺点，得到了大范围的推广与应用。同时，范千等[10]发现，加入小波变换后的预测模型对滑坡位移的预测更加准确，小波变换从而被大范围应用于滑坡的位移预测[9， 11-14]。

基于以上研究背景，以阿海水电站附近某滑坡获得的全球定位系统(global positioning system，GPS)监测数据为例，首先将滑坡累计位移进行小波分解处理，将位移数据分解为趋势项位移和周期项位移，应用核极限学习机(kernel-based extreme learning machine，KELM)对各分项位移进行预测，并使用麻雀搜索算法(sparrow search algorithm， SSA)对核极限学习机的各项参数进行寻优，最后将趋势项位移和周期项位移相加得到最终预测结果。将预测结果与支持向量机模型做对比，以均方根误差、平均相对误差绝对值和相关性系数三项指标评价滑坡预测模型的精度。

1 改进的SSA-KELM模型

1.1 小波分解

小波分解是采用非周期信号，通过应用基函数的不同尺度缩放去拟合被测信号的不同频率，再通过平移基函数去拟合不同频率分量在时间序列上位置的过程。小波变换可分为连续小波变换和离散小波变换两大类。

选择使用一维离散小波变换，离散小波基函数ψj，k(x)为

(1)

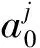
因此，信号f(x)的离散小波变换可表示为

(2)

1.2 麻雀搜索算法

麻雀搜索算法是一种新型的群智能优化算法，在2020年由Xue等[15]提出，主要是受麻雀的觅食和反哺食行为启发，具有寻优能力强、收敛速度快的特点。

麻雀搜索算法将整个麻雀种群分为三类，即寻找食物的生产者，抢夺食物的加入者和发现危险的警戒者。生产者和加入者可以相互转化，但各自在种群中的占比不会发生变化。

在模拟实验中，需要使用虚拟麻雀进行食物的寻找，与其他寻优算法相同，麻雀搜索算法首先需要对麻雀种群与适应度值进行初始化，麻雀种群可初始化为如下形式，表达式为

(3)

式(3)中：n为麻雀的数量；d为要优化的变量的维度即独立参数的数目；xn，d为第n只麻雀第d维度的值。

由此，总体麻雀适应度值表征形式为

(4)

式(4)中：f(x)为个体适应度值。适应度值较好的麻雀(即生产者)在搜索中会优先获得食物并指引群体的觅食方向与范围，与此同时，生产者会具有更大的觅食搜索范围。

生产者在觅食过程中，位置不断发生移动，而在遇到捕食者时，移动规则又会发生改变，即

(5)

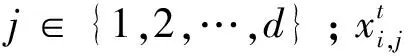
而对加入者而言，在觅食过程中，一旦生产者找到了好的食物源，加入者必会知晓，并飞向它的附近抢食，同时，也有加入者会时刻监视生产者，随时准备争抢食物。由此加入者的位置更新规则为

(6)

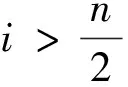
总体而言，假设意识到危险的麻雀(即警戒者)占10%～20%。初始位置则随机产生，规则为

(7)

式(7)中：λ为步长控制函数，是一个均值为0，方差为1的正态分布随机数；fi为当前麻雀适应值；fg为全局最好适应值；fw为全局最差适应值；k为麻雀移动方向；xbest为全局最优位置；ε为最小常数，避免除数为零。当fi>fg时，警戒者位于种群边缘，意识到危险后向中央安全区靠近；当fi=fg时，则是处于种群中央的麻雀意识到了危险，为躲避危险，则向其他麻雀身边靠拢。

1.3 核极限学习机算法

传统的单隐层神经网络由三部分组成，分别是输入层、隐含层和输出层，输入层神经元节点个数即输入变量的个数，隐含层节点个数则需要人为给定，输出层节点个数也就是输出变量的个数。

在2006年，新加坡南洋理工大学的Huang等[16]在传统的单隐层神经网络的基础上提出了一种新的前馈神经网络学习算法，命名为极限学习机(extreme learning machine， ELM)，不同于传统的基于梯度的前馈神经网络算法，该方法随机产生隐含层与输入层之间的连接权值及隐含层神经元的阈值，训练过程中只需要设置隐含神经元的个数便可获得唯一最优解，极限学习机网络结构如图1所示。

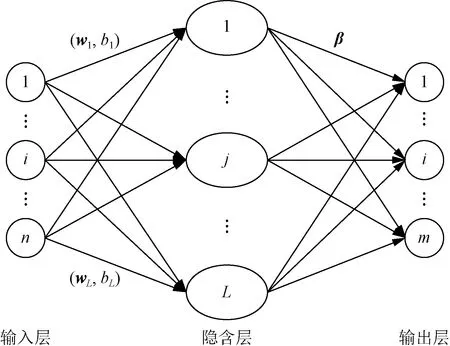
图1 极限学习机的网络结构Fig.1 Network training model of ELM

在极限学习机中，假设有N个随机样本，设其为(Xi，ti)，其中，xi=[xi1，xi2，…，xin]T∈Rn，ti=[ti1，ti2，…，tim]T∈Rm，R为实数，则对于具有L个隐含层神经元的单隐层神经网络，它第i个节点的输出hi(x)可表示为

hi(x)=g(wi，bi，xi)=g(wi·xi+bi)

(8)

式(8)中：wi为输入权重；bi为第i个隐含层神经元的阈值；wi·xi为wi和xi的内积；g(x)为一个任意区间无限可微的激活函数，激活函数可自行设置，常用的激活函数有sig、sin、hardlim等，但也有研究表明，激活函数既可以是非线性函数，也可以为不可微函数或不连续函数。

则隐藏层输出矩阵为

H(x)=[h1(x)，h2(x)，…，hL(x)]

(9)

由此，输出层可表示为

fL(x)=H(x)β

(10)

式(10)中：β=[β1，β2，…，βL]T为隐藏层与输出层之间的输出权重。

由式(8)～式(10)可知，极限学习机中需求解的有3个未知量：w、b、β。通过ELM的特殊性质来求解。ELM对单隐层前馈神经网络的训练主要分为如下两个阶段。

(1)随机特征映射。即随机产生隐含层的参数w和b，在传统的反向传播(back propagation，BP)神经网络中，这两个参数通过计算得来，而ELM的做法则大大提升了运算效率。

(2)线性参数求解。在确定了输入权重w和隐含神经元阈值b之后，通过式(8)、式(9)可求得隐藏层的输出矩阵H，进而通过最小化近似平方差的方法对β进行求解，目标函数如下：

min‖Hβ-T‖2，β∈RL×m

(11)

其中，期望矩阵为

T=[T1，T2，…，TN]T

(12)

输出矩阵为

H=[h(x1)，h(x2)，…，h(xN)]T

(13)

其解为β*=H†T，其中，H†为矩阵H的Moore-Penrose广义逆矩阵。

因为ELM中的输入权重w和隐含神经元阈值b是随机产生，算法效果不稳定，所以之后Huang等[17]为了算法的准确性和稳定性，又在算法中引入了核参数，使其代替ELM的随机特征映射，形成核极限学习机算法。

通过正交投影和岭回归(ridge regression)理论，引入正则化系数C，则输出权重可表示为

(14)

因此输出函数

(15)

式(15)中：K(x，xi)为核函数。

1.4 模型建立

利用麻雀搜索算法对核极限学习机的两项参数：核参数K及正则化系数C进行优化，得到SSA-KELM耦合滑坡预测模型，其实施步骤如下。

步骤1初始化种群。设置麻雀数量为20，随机产生初始核参数K及正则化系数C，生成种群初始位置。

步骤2确定优化参数的取值范围。根据多次实验，确定核参数K为(-1010，1010)，正则化系数C为(-1010，1010)。

步骤3建立SSA-KELM耦合模型，计算麻雀个体适应度f(xi)，i=1，2，…，n，对适应度值进行排序，寻找出当前最好和最差的个体。适应度函数为

(16)

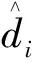
步骤4根据式(5)～式(7)更新麻雀位置。

步骤5获取新的麻雀位置及个体适应度值，将本轮最优适应度值与之前的最优适应度值做比较，如果本轮更优，则更新全局最优适应度值Gbest与相关位数。

步骤6循环结束。当迭代次数大于500，则寻优过程结束。

步骤7得到KELM的最佳训练参数，模型建立。

改进的SSA-KELM模型滑坡预测流程如图2所示，算法结构如图3所示。

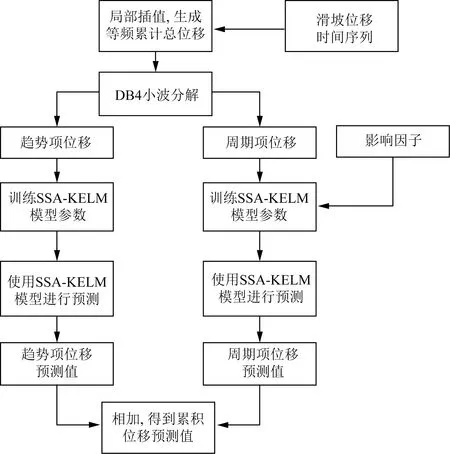
图2 改进的SSA-KELM模型滑坡位移预测流程图Fig.2 The flow chart of landslide displacement prediction based on the improved SSA-KELM model

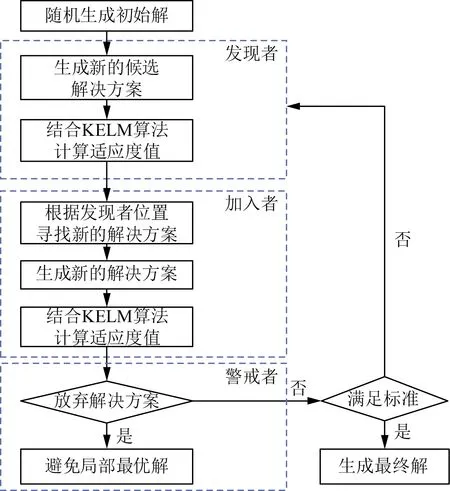
图3 改进的SSA-KELM算法框架Fig.3 The framework of the improved SSA-KELM algorithm

2 模型精度评价

使用三项指标来评定模型精度，分别为均方根误差(root mean square error，RMSE)、平均相对误差绝对值(mean absolute percentage error，MAPE)和相关性系数(R)。RMSE和MAPE的值越小，预测效果越好；R越大，则预测效果越好。各精度评价指数的计算公式如下。

(1)均方根误差。

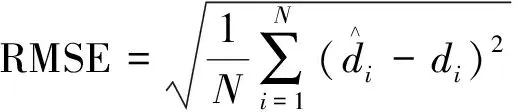
(17)

(2)相关性系数。

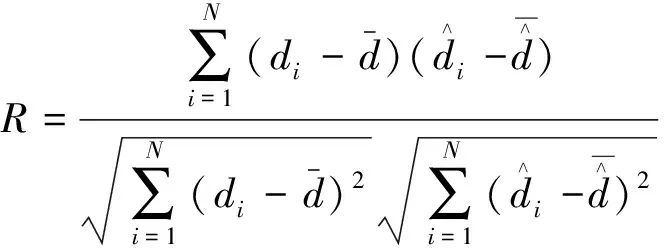
(18)

(3)平均相对误差绝对值。

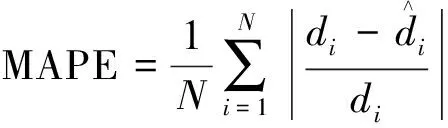
(19)

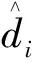
3 研究区概况

研究区滑坡位于金沙江中游阿海水电站左岸，距坝址约37 km，沿南北向分布，纵向长度约1.5 km，宽约600 m，滑坡体总方量约6 970×104m3，该滑坡体属中厚层混合特大型堆积体，其前端有塌滑现象，地形呈圈椅状，地貌特征明显，为仍在活动的滑坡。从资料来看，造成滑坡的原因有以下三方面。

(1)堆积体原始岸坡前缘较陡，阿海水电站水库体地下水位线抬升，部分岩(土)体处于饱水状态，物理力学性质(如含水量、干重度、孔隙比等)发生了改变；堆积体前缘库岸再造，局段出现崩塌、小滑坡，形成新的临空面；水位变化产生动水压力，受力状态发生改变。

(2)2013年雨季降雨，大量的雨水集中下渗，下渗水流对堆积物的结构、物理力学性质产生了一定程度的恶化作用。

(3)人类活动(建房、修路、生产生活用水排放等)改变了堆积体地表形态，并恶化了稳定条件。

综上，由于库水浸泡和水位变化及降雨下渗，加之人类工程活动影响，打破了堆积体原有的平衡条件，导致大范围产生滑移变形。

4 滑坡变形监测

该滑坡上布设有15个GPS监测点， GPS数据平时每隔3个月采集一次，雨季的7—9月每个月采集一次，合计每年6～7次。同时，该滑坡体还设有一个GPS自动监测站，进行24 h实时监测。该数据波动比较大，原因主要是测量间隔较短(实时监测)，但变形趋势与附近人工监测点趋势相吻合。GPS监测点布设状况如图4和图5所示。

5 滑坡位移预测

考虑到GPS点监测时间的连贯性与监测数据的变化幅度大小，选用2013年1月—2018年底Ⅲ区的GPS滑坡监测数据作为实验样本，由监测点位移时间曲线(图5)可知，选取滑坡变形时间最长、累计位移量最大且平均变形速率最快的XJ17监测点作为研究对象，选择2013年1月—2018年1月的数据作为模型训练集，2018年2月—2018年底的数据作为预测集。实验在MATLAB2018b软件中进行。

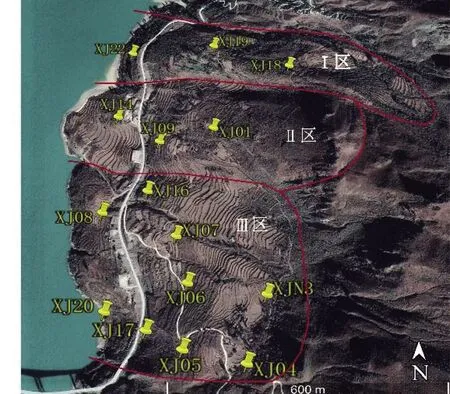
图4 滑坡体及其周边监测点布置图Fig.4 Layout of monitoring points of the landslide and its surrounding bodies

5.1 数据预处理

(1)对GPS点XJ17进行线性插值，得到等间距的位移时间序列。

(2)使用db4小波变换，根据式(1)和式(2)将插值后的位移时间序列分解为趋势项位移与周期项位移。

(3)对分解后的数据进行线性函数归一化处理，统一映射到[-1，1]区间内。如此，既可提高函数寻优速度，也在一定程度上提高了求解的精度。归一化公式为

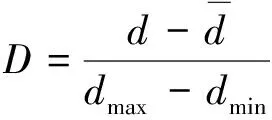
(20)

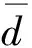
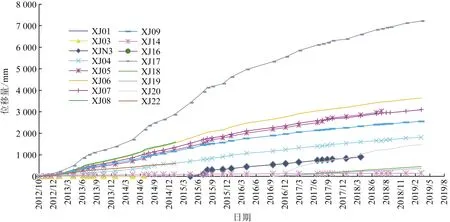
图5 GPS监测点位移-时间曲线Fig.5 Curves of cumulative displacement of GPS monitoring points vs time

5.2 趋势项位移预测

趋势项位移代表了多年以来滑坡变形的总体趋势，是滑坡位移预测中最为关键的一项。采用改进的SSA-KELM算法对趋势项位移进行预测，寻优得到的正则化系数C为1010，核参数K为-0.265 4，将预测结果反归一化后与SVM进行对比，对比结果如图6所示。

从精度对比表1中可知，SSA-KELM对趋势项的预测结果更好。同时，算法的收敛曲线如图7所示，可以看到，预测算法收敛速度很快。

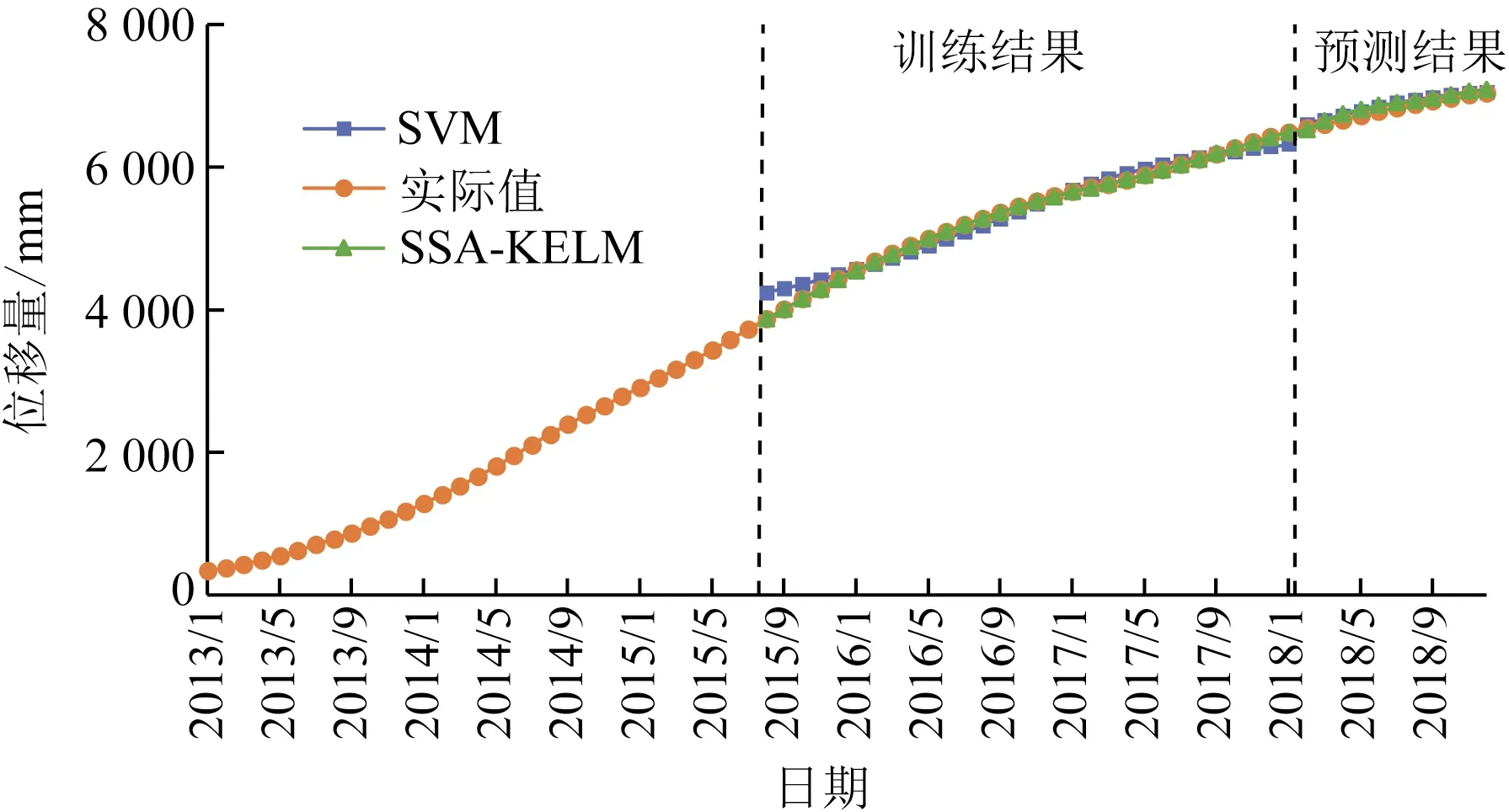
图6 不同模型趋势项位移预测结果对比Fig.6 Comparison between predicted and measured trend displacement by different models

表1 不同模型趋势项位移预测模型精度对比Table 1 Prediction performance comparison of trend displacement by different models

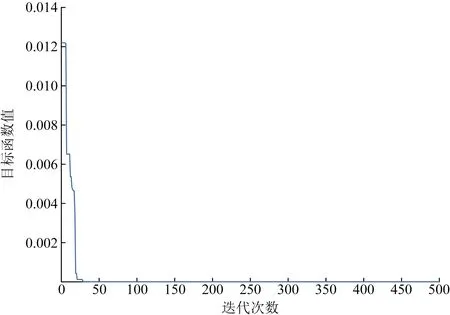
图7 趋势项位移预测模型收敛曲线Fig.7 Convergence curve of trend displacement prediction model

5.3 周期项位移预测

选取当月降雨量、双月降雨量、滑坡当月位移增量、前两月位移增量和前三月位移增量作为影响因子[18]对XJ17点进行对比分析，变化趋势如图8所示。

采用灰色关联度法计算影响因子与周期项位移之间的关联度，其关联度如表2所示，关联度均大于0.6，表明所选影响因子与周期项位移之间具有强相关性。

将影响因子和周期项位移训练集中的数据作为模型输入项，通过麻雀搜索算法寻优得到KELM的最优训练参数C=-3.08×1010，K=1010，进而得到反归一化后的预测结果，为检验该算法预测效果，引入支持向量机算法与模型预测效果进行对比，其对比曲线如图9和表3所示。

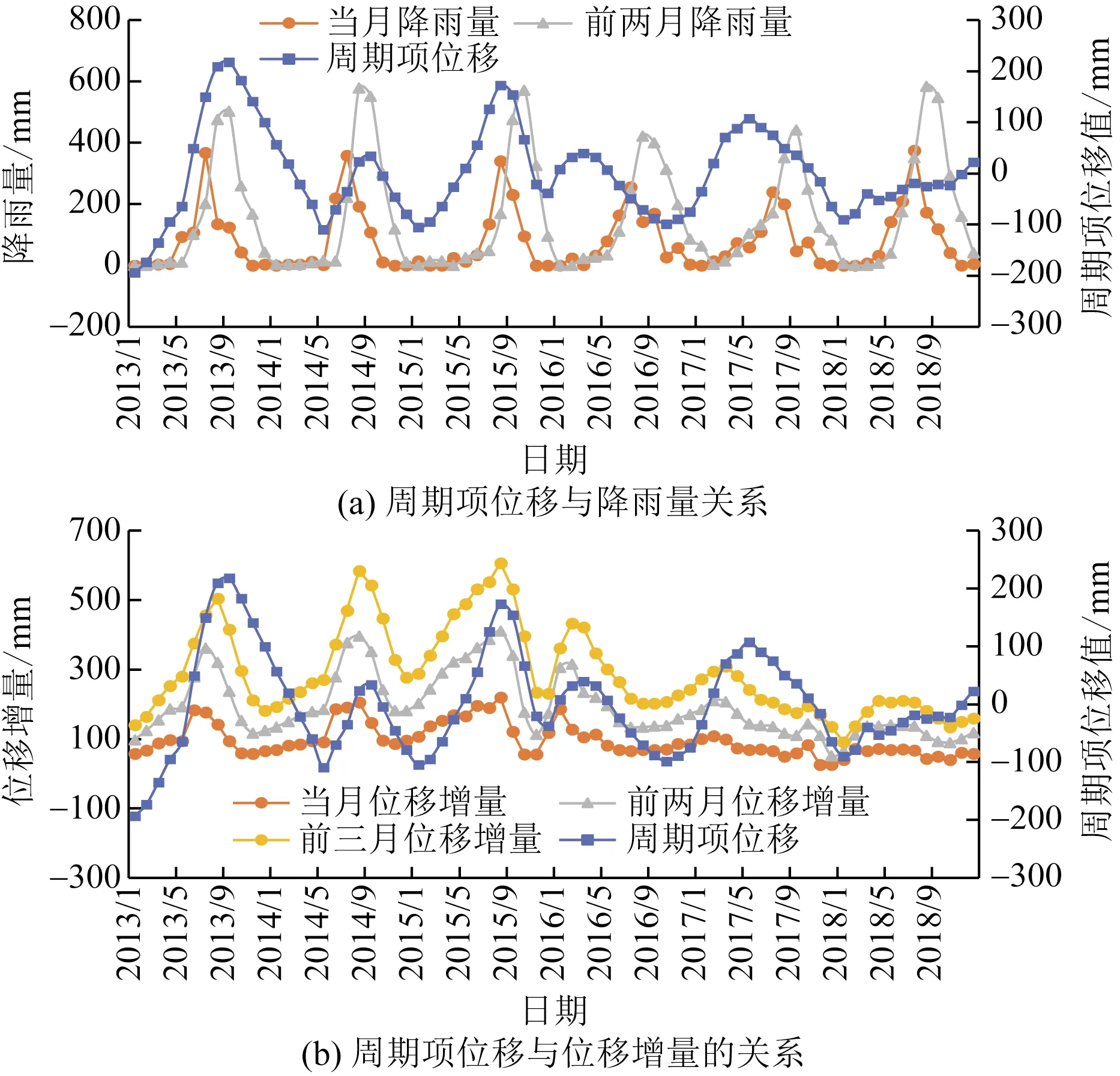
图8 周期项位移与影响因子关系Fig.8 Relationships between periodic displacement and influence factors

表2 周期项位移与影响因子关联度Table 2 Degrees of gray correlation between the period term displacement and influence factors

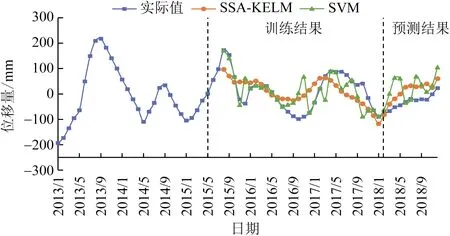
图9 不同模型周期项位移预测结果对比Fig.9 Comparison between predicted and measured periodic displacement by different models

在周期项位移预测结果中可以看到，虽然两种预测模型的预测结果与实际值都有一定差距，但相比SVM，改进的SSA-KELM预测模型在各项评价参数上明显更优，拟合效果更好，其算法收敛曲线如图10所示，收敛速度较快。

同时，对该点进行多次预测实验，算法寻优结果与位移预测结果均不变，说明算法具有很好的稳定性。

表3 不同模型周期项位移预测精度对比Table 3 Prediction performance comparison of periodic displacement by different models

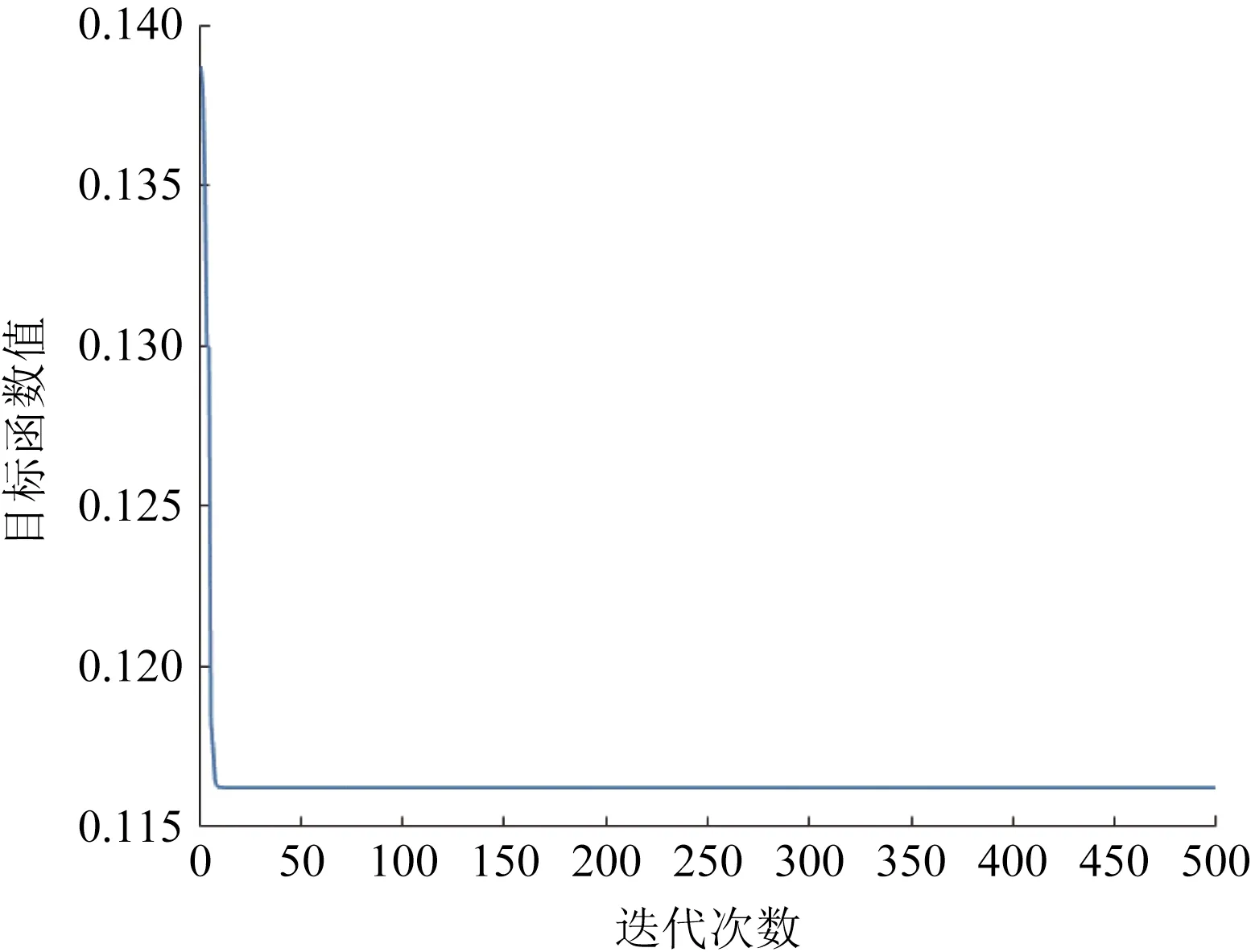
图10 周期项位移预测模型收敛曲线Fig.10 Convergence curve of periodic displacement prediction model

5.4 滑坡累计位移预测

将预测得到的周期项位移和趋势项位移结果相加，得到的最终累计位移预测结果如图11和表4所示。

使用同样的方法对监测点XJ04进行预测，两种方法的预测结果如图12和表5所示。对XJ04和XJ17两点的预测结果表明，相比SVM模型，改进的SSA-KELM模型对滑坡位移的整体预测精度更高，新模型具有较好的普适性。

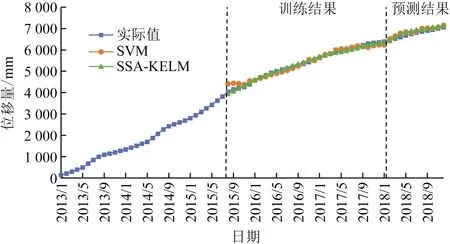
图11 XJ17的累计位移预测结果Fig.11 Cumulative displacement prediction values of XJ17

表4 累计位移预测精度对比表(XJ17)Table 4 Prediction performance comparison of cumulative displacement by different models(XJ17)

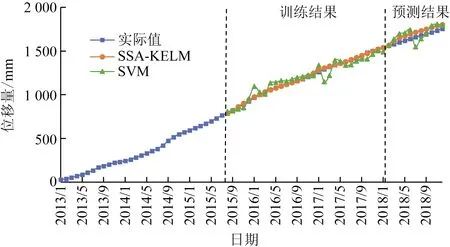
图12 XJ04的累计位移预测结果Fig.12 Cumulative displacement prediction values of XJ04

表5 累计位移预测精度对比表(XJ04)Table 5 Prediction performance comparison of cumulative displacement by different models(XJ04)

6 结论

(1)提出了一种基于改进的SSA-KELM耦合算法的滑坡位移预测模型。通过使用麻雀搜索算法对核极限学习机的正则化系数与核参数进行寻优，只需设置麻雀数量和最大迭代次数两项参数，便可取得位移预测结果，相比传统的需要设置大量参数的SVM算法，该预测模型需要人为干预的参数更少。

(2)对XJ04和XJ17两点的预测结果表明，改进的SSA-KELM算法相较于传统的SVM算法预测精度更好，该算法具有较高的稳定性和较好的普适性，是一种准确有效的滑坡预测模型。

(3)由于获取的GPS数据不可避免地存在人为误差和系统误差，同时获取GPS数据的时间间隔不等，最终预测效果也必然受到影响。在条件允许的情况下，更多的GPS监测数据与相关影响因子(如地下水位、库水位等)的加入将更有利于模型的训练与预测。