基于混合热格子Boltzmann方法有限热源加热气泡动力学模拟

金志浩， 章港， 战洪仁， 李帅， 王立鹏， 张志刚

(沈阳化工大学机械与动力工程学院， 沈阳 110142)

沸腾是一种高效的传热方式，近些年来，对于沸腾传热机理以及强化沸腾传热的研究，已经成为国际上沸腾领域的研究热点。此研究对于提升能源利用效率、减少工程投资有着重要意义。随着电子元器件的集成化越来越高，普通的风冷已经无法满足电子元件的散热需求，采用沸腾散热已经成为必然的趋势，近些年，通过调控加热表面的润湿性来强化沸腾传热已成为研究热点之一，很多学者通过实验对亲疏水表面沸腾传热的影响进行了研究。Takata等[1]通过在铜表面镀聚四氟乙烯(polytetrafluoroethylene，PTEE)颗粒获得疏水表面，发现疏水表面在加热面温度低于饱和温度时，就能形成稳定膜态沸腾。Theofanous等[2-3]通过红外相机观察壁面润湿性对气泡脱离直径有较大的影响。Fan等[4]通过实验发现随着壁面润湿性的增加，气泡脱离频率降低。Jo等[5]通过实验研究了接触角对换热特性的影响。姜洪鹏等[6]用激光烧蚀方法在抛光后的铜上制备出超疏水/亲水性的规则微阵列结构表面，发现疏水表面尾端气泡容易汇聚，生长周期较长；而亲水表面没有发生明显的气泡汇聚行为，气泡生长周期较短。但是沸腾传热过程的影响因素众多，在实验研究中难以区分，使得实验结果的准确性受到质疑，而且通过实验很难观测气泡生长、脱离过程的微观流动细节，无法详细描述出气泡生长的内在机理。

随着计算机技术的飞速发展，流体体积法(volume of fluid，VOF)[7-9]、Level Set[10]、界面追踪法(front tracking method，FTM)方法[11]及格子Boltzmann方法等数值模拟方法得到了广泛的发展，并且已应用于研究沸腾和冷凝相变过程。但VOF、Level Set及FTM等数值模拟方法需要精确追踪汽液界面，在气泡和液滴的生长与脱离的过程中，追踪汽液界面演化的方法并不能很好地满足要求。此外，在应用这些数值方法模拟相变时，需要预先设置汽化/液化核。所以这些都意味着用传统的计算流体力学方法模拟受限空间内沸腾相变的传热过程仍然是一个挑战。近些年，飞速发展起来的格子Boltzmann模型，在并行性和自动追踪相界面方面具有固有的优势，已成为探索相变现象的强大的数值模拟工具。Boltzmann模型主要有自由能模型[12-14]、伪势模型[15-17]、颜色模型[18-20]三种模型形式。伪势模型[15]有着极高的稳定性，可应用于大规模计算仿真、多相多组分仿真以及特定复杂流体情况和边界条件时的仿真计算。但该模型存在密度比小，且模拟方法的稳定性较差，严重限制了格子Boltzmann方法的实际应用，为解决此问题，Zhang等[21]首次将格子Boltzmann伪势模型与有限差分法结合，并模拟大空间气泡脱离的过程。Dong等[22]提出一种新的自由能模型，对热格子Boltzmann模型进行了扩展与发展，形成混合格子Boltzmann模型。Gong等[23]在伪势模型基础上提出一个新的源相，提高数值稳定性，并把P-R状态方程代入格子Boltzmann方程，验证格子Boltzmann结合P-R状态方程稳定性。Gong等[24]又提出一种引入流固张力的模型，使得壁面接触角可以在0～180°调整，研究了池沸腾亲疏水壁面气泡生长传热过程。Gong等[25]基于P-R状态方程的格子Boltzmann模型，用该模型模拟了大空间多气泡生长过程。Li等[26]提出一种模拟多相流的混合热格子流密度，研究了临界热流密度以及池沸腾气泡的成核过程。汪鹏军等[27]通过将密度分布函数与温度分布函数进行耦合求解的方式建立了气液相变模型，研究了气泡脱离直径与重力加速度的关系。综上所述，运用格子Boltzmann方法对沸腾的研究，主要集中于大空间多气泡核态沸腾。而多气泡沸腾传热包括一系列气泡生长、脱离、多气泡的相互作用及表面粗糙度状况等较多的影响因素，不利于从表面润湿、过热度等单一因素研究气泡的生长机理及动力学特征，因此应用格子Boltzmann数值模拟研究讨论单气泡的生长过程，可有效避免多气泡相互作用而产生非线性现象的影响，对多气泡的运动特性的研究有重要意义。

现基于混合热格子Boltzmann模型，建立单气泡生长过程的数值模型，从微观角度在不同润湿性表面、不同有限热源长度、不同过热度等单一影响因素条件下，对单气泡产生、长大、脱离过程的动力学特点进行模拟研究，并通过流场和温度场对获得的气泡形态及气泡生长过程的影响因素进行分析和比较，为研究强化表面沸腾传热及表面润湿性的选择提供理论依据。

1 基本模型

采用单组多相伪势格子Boltzmann模型[18]耦合能量方程模拟气液相变过程，其中单组多相伪势格子Boltzmann模型密度演化方程具体表达式为

fi(x+eiδt，t+δt)-fi(x+t)

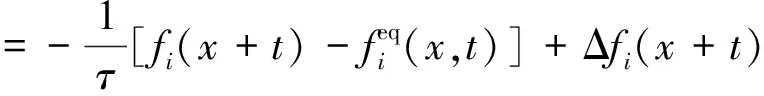
(1)

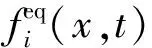
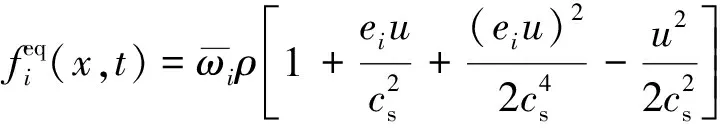
(2)

格子点的密度ρ与速度u计算公式为

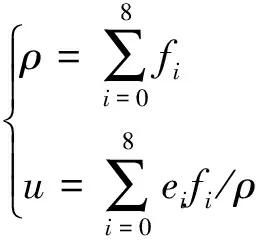
(3)

所以格子点的密度ρ为单位格子上各个方向粒子分布函数之和。

在多相流的模拟中，体积力是十分重要的，诸多学者[12]用精确差分方法求解体积力项，这样可以保证方程稳定性，关系式为

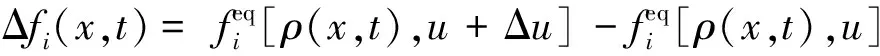
(4)

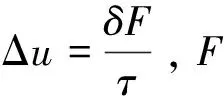
为了使气液两相分离，引入流体间粒子作用力Fint，表达式为

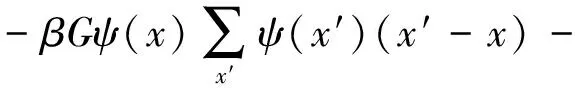
(5)

式(5)中：β为提高计算稳定的权重因子，取值1.16；G为相互作用常数，取值-1；x′为x的相邻格子点坐标；ψ(x)为有效密度，与流体状态方程有关，表达式为

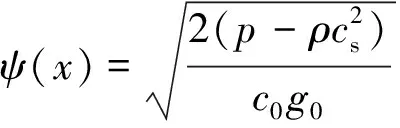
(6)

式(6)中：p为流体压力；g0为流体作用系数;c0为格子系数。

通过引入Fs可获得不同的三相接触角，Fs表达式为

(7)

式(7)中：sw为用来判断格点是否是壁面的函数，对于固体壁面，可以取1，对于流体取0；Gw为流体与固体壁面的作用常数。

重力Fg表达式为

Fg=g(ρ-ρave)

(8)

式(8)中：g为重力加速度；ρave为计算域内密度平均值。

模拟气液相变现象，还需要在单组份多相伪势模型的基础上，耦合能量方程[28-29]构成相变模型。能量方程为

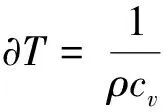
(9)

宏观速度U计算公式为

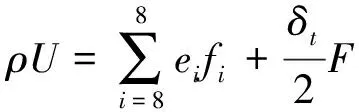
(10)

压力ρ可运用控制流体状态的P-R状态方程确定，即

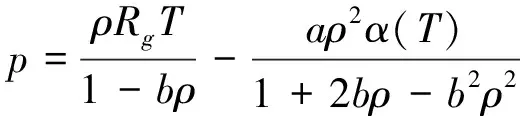
(11)

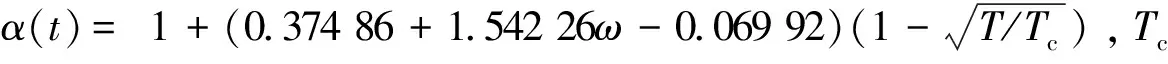
最后对温度场采用二阶龙格库塔法离散，获得区域温度场温度分布，二阶龙格库塔方法表达式为

(12)

2 初始化模型与量纲分析

2.1 初始化模型与程序验证

宽Lx=200，高Ly=250的封闭空间中充满饱和温度Tf=0.86Tc的气液两相流体，经过网格独立性验证，计算域200×250可保证数值稳定性。建立物理模型图如图1所示，为保障在容器底部产生单气泡，在底部中心处设置加热长度为3个格子长度的有限长度恒温热源P，加热温度Ts=1.3Tc。容器左右侧壁面取周期边界条件[31]，上下壁面取Zou-He边界条件[32]。

调整重力加速度g的取值分别为-0.000 01、-0.000 02、-0.000 03、-0.000 04、-0.000 05，获得不同气重力加速度下泡脱离直径曲线(图2)， 横坐标g为重力加速度，纵坐标D代表气泡脱离直径，其中单位为格子长度。气泡脱离直径与重力加速度g的拟合函数关系为D-g-0.5，符合Fritz提出的半经验公式，说明程序可靠。

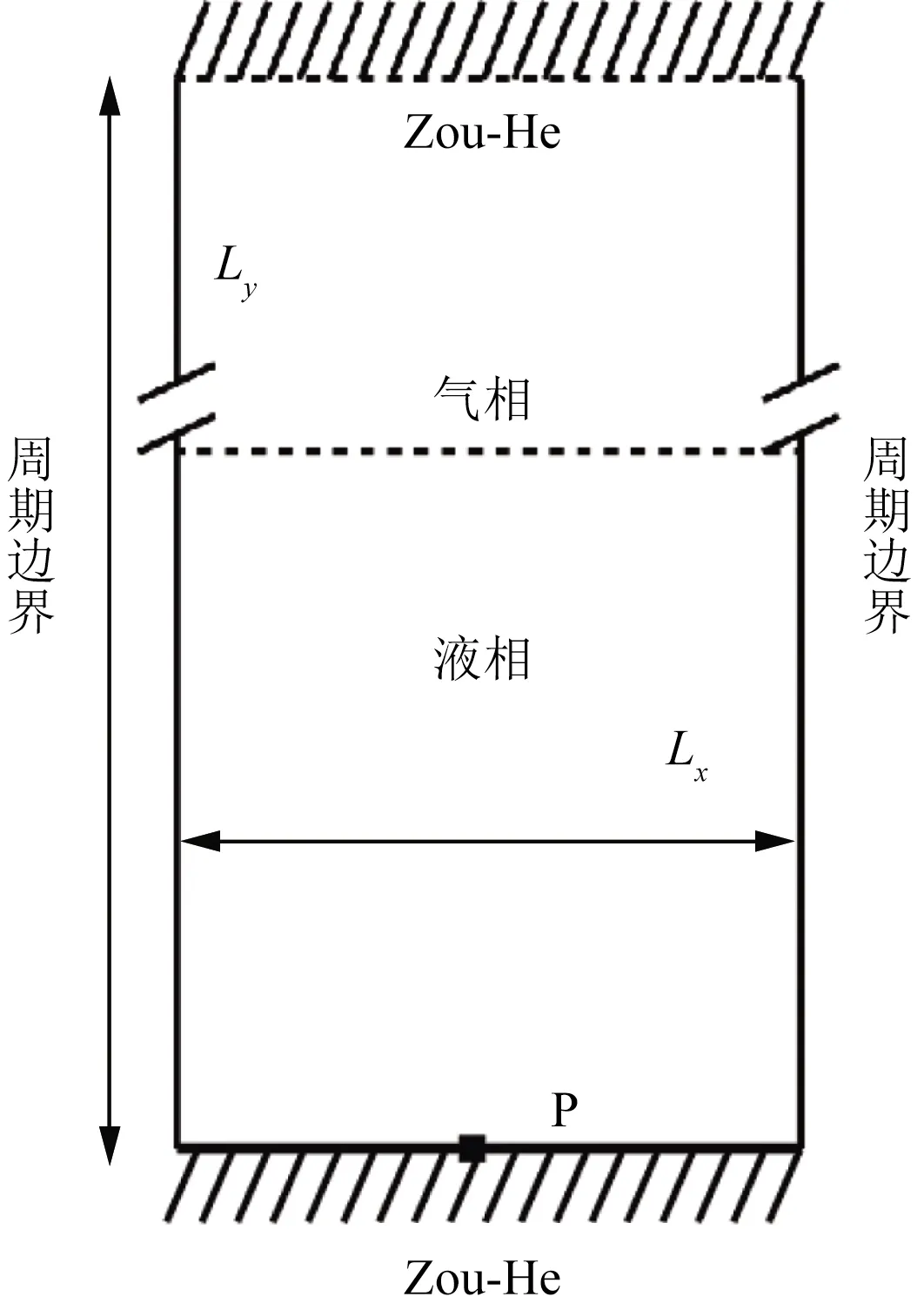
图1 物理模型Fig.1 Physical model

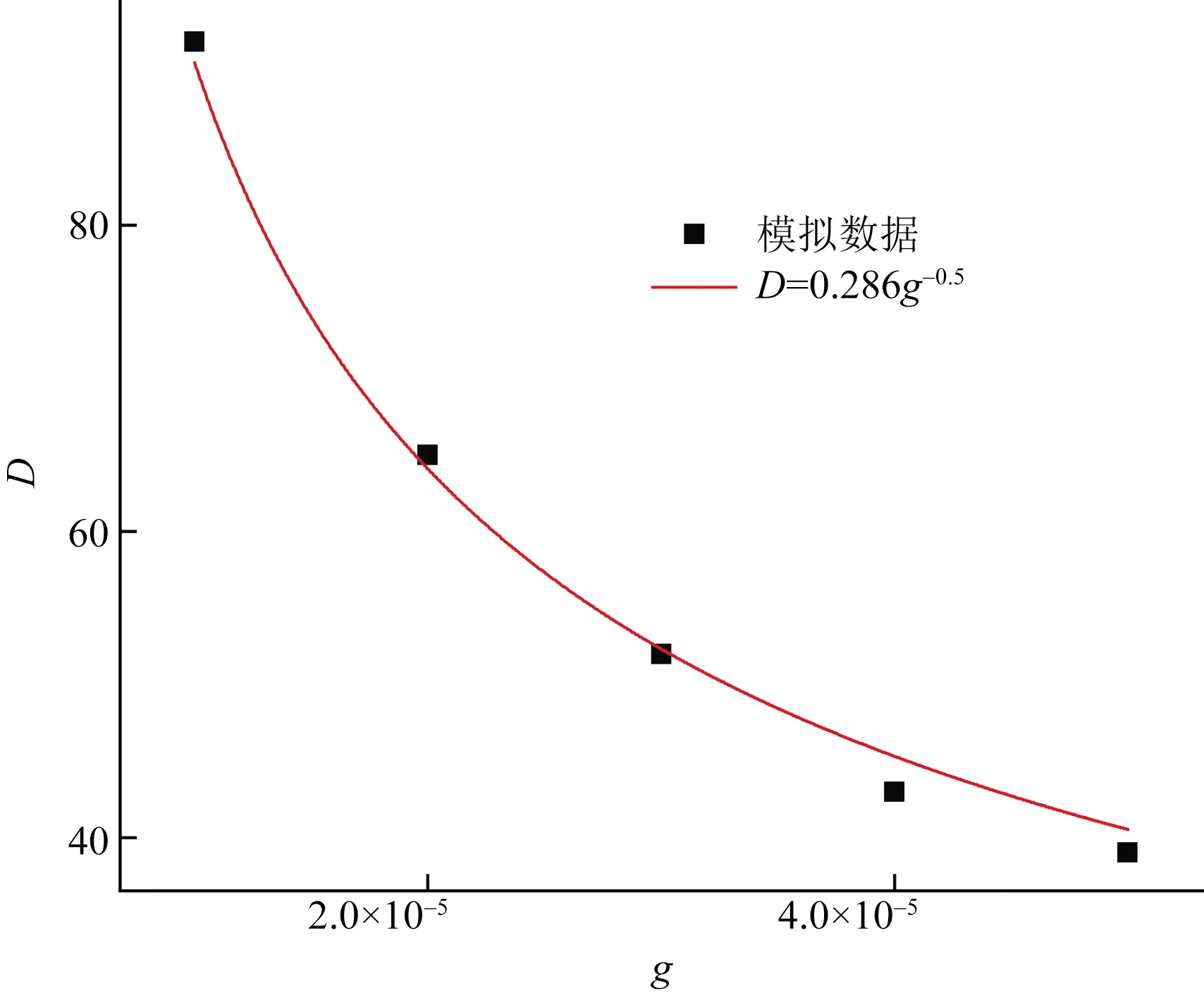
图2 重力加速度g与气泡脱离直径D关系Fig.2 The relationship between gravitational acceleration g and detachment diameterD

2.2 无量纲转换

格子Boltzmann模拟中用格子单位表示物理量，特征长度l0通常用来描述气液相变过程，相对应的特征时间t0是由特征长度l0除以特征速度u0得到，计算公式[25]为

(13)

式(13)中：ρl为饱和液体密度，取值6.5；ρv为饱和气相密度，取值0.38；σ为表面张力。因此，无量纲长度l*和无量纲时间t*分别定义为

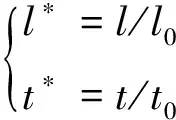
(14)

因此无量纲直径计算方法为

D*=D/l0

(15)

无量纲温度计算方法为

T*=T/Tc

(16)

式(16)中：Tc流体的临界温度；T为流体的温度；T*为无量纲温度。

过热度计算方法为

ΔT=Ts-Tf

(17)

式(17)中：Ts为恒温热源加热温度；Tf为饱和温度。

3 计算结果与分析

首先初始时刻在容器底部壁面处放置密度为6.5的液滴，周围充满密度0.38的气体，通过调整Gw数值，改变流体与固体壁面之间作用力，待程序运行稳定后，分别获得不同三相接触角的壁面，表明不同亲疏水表面，如图3(a)、图3(b)、图3(c)、图3(d)所示，黄色代表放置的液滴，蓝色代表空间中的气体，其中图3(a)、图3(b)为亲水壁面，图3(c)、图3(d)为疏水壁面。

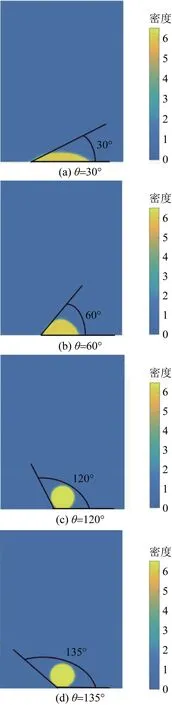
图3 不同壁面三相接触角Fig.3 Three phase contact angle on different wall surfaces

3.1 亲疏水壁面气泡生长过程

图4和图5分别为在接触角为60°的亲水表面上单个气泡生成、成长和脱离流线图和温度场。初始时刻，在有限热源附近形成一个过热边界层，如图5(a)所示。随着加热时间的推移，由图5(b)可以观察到过热边界层内产生一个气泡核，气泡核内的蒸汽温度升高，气泡内的温差增大，导致气液压差加大，气泡内部流体的速度大于气泡外的速度，依靠惯性作用推动气泡核快速生长，这时亲水表面的气泡是以圆形状态逐渐生长，而这个阶段气泡体积小，其对外部流场扰动可忽略，如图4(a)、图4(b)所示。随后气泡内部惯性作用逐渐减小，气泡的长大主要依靠过热液膜提供热量，液相转化为气相，加快周围冷流体回流，在有限热源两侧逐渐形成反方向旋转的涡流，致使底部热边界层温度降低，热边界层提供热量不足以支撑气泡快速生长，如图5(c)所示。此时气泡生长形态在表面张力、浮力流场剪切力作用下由圆形被拉成椭圆形，并在近壁面处形成颈部，图4(c)、图4(d)所示为气泡生长阶段。图4(e)、图4(f)为气泡的脱离阶段，可以观察到气泡脱离壁面，这是由于在贴壁处气膜的气化需要液体补充，冷流体的回流冲击，强化在壁面处形成两个反方向的涡流。在流场剪切力、浮力、壁面张力的拉扯下，气泡颈部紧缩，壁面张力急剧减小，最终导致气泡脱离。图5(d)为气泡脱离温度场，气泡脱离后，有限热源附近又形成一层热边界层，气泡脱离的尾流对热边界层带来巨大的扰动。

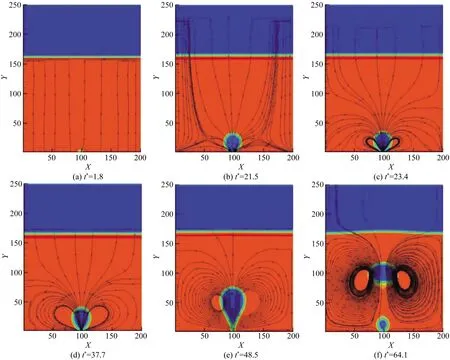
图4 接触角60°亲水壁面气泡生长流线图Fig.4 Bubble growth flow diagram on hydrophilic wall with contact angle of 60°

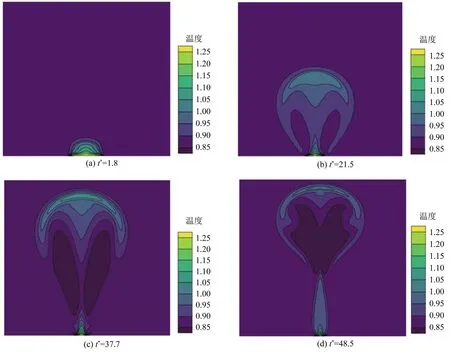
图5 接触角60°亲水性壁面气泡生长过程无量纲温度场Fig.5 Dimensionless temperature field during bubble growth on hydrophilic wall with contact angle of 60°

图6、图7为接触角为120°的疏水壁面气泡生长脱离过程流场图和温度场。起初在有限热源附近形成过热边界层中，如图6(a)、图7(a)所示，随后在过热边界层内形成气泡核，由于气泡内蒸汽温度较高，气泡快速向外膨胀，在惯性力和表面张力作用下，气泡沿着疏水壁面延伸生长，致使气泡与疏水壁面三相线长度不断增大，同时可观察出疏水壁面气泡两端有着反方向旋转的涡流，该涡流破坏边界层强化换热，加速气泡生长，如图6(b)和图7(b)所示的气泡成核阶段。而在图6(c)、图6(d)气泡生长阶段，气泡在疏水壁面的三相线长度缩小，主要原因是随着气泡生长惯性力逐渐减小，气泡浮力不断增大，气泡垂直向上增长。气泡向上生长两侧形成较大的涡流，该涡流促进气泡在中间紧缩，形成颈部。随着涡流的增强，气泡内部分布的温度梯度逐渐减弱，热量不足以支撑气泡快速生长，气泡生长速度减慢，如图7(c)所示。在图6(e)、图6(f)气泡脱离阶段中，气泡在中间断裂脱离，这是由于冷流体回流较大，在两侧形成较强循环，在流场剪切力与气液张力的拉扯下，在中间形成颈部，直至断裂脱离。然而由于疏水壁面表面张力过强，依然有部分气泡附着在疏水表面上作为下一个气泡的汽化核心。如图7(d)所示，气泡脱离后带走一部分热量，气泡脱离形成尾流，促使热边界层扰动。在气泡生长、脱离过程中，温度场与流场相互作用，促使气泡成核、生长、脱离。

图6 壁面接触角120°疏水性壁面气泡生长流线图Fig.6 Hydrophobic wall bubble growth flow diagram with contact angle of 120°

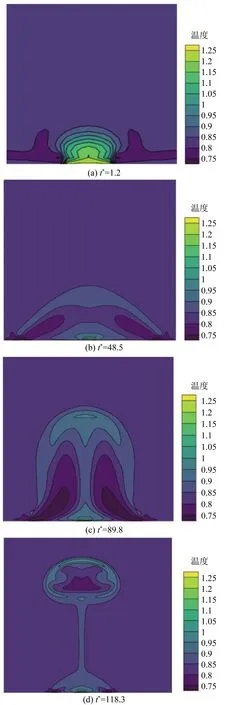
图7 壁面接触角120°疏水性壁面气泡生长 无量纲温度场Fig.7 Dimensionless temperature field of hydrophobic wall bubble growth with contact angle of 120°

3.2 气泡生长无量纲直径与无量纲时间的关系

图8表示在相同的过热度下，亲疏水壁面气泡生长大小、脱离与时间关系图，可以看出，亲疏水壁面气泡生长曲线先快速上升，随后缓慢上升，最后保

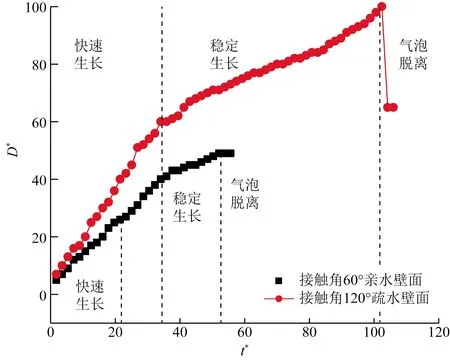
图8 亲疏壁面气泡D*与t*关系Fig.8 The relationship of bubble growth D*with t* on close and thin wall surfaces

持不变。疏水壁面气泡脱离后，壁面有部分气泡残留，因此疏水壁面产生的气泡大幅度减小。无论是亲水壁面还是疏水壁面。分析可知，都存在快速生长阶段、稳定生长阶段、气泡脱离3个阶段，其中快速生长阶段气泡快速膨胀，稳定生长阶段气泡生长速度减慢，脱离阶段气泡不再生长，其内在原因已在温度场中论述。还可以观察到疏水壁面较亲水壁面先产生气泡。疏水壁面曲线增长速率大于亲水壁面，说明疏水壁面气泡生长速度大于亲水壁面气泡生长速度。疏水壁面曲线增长速率大于亲水壁面，说明疏水壁面气泡生长速度大于亲水壁面气泡生长速度。疏水壁面气泡脱离时刻有2个气泡无量纲直径，分别是100和61，说明由于疏水壁面具有亲气疏水的特性，气泡脱离时被分成了2部分，一部分气泡脱离壁面，其直径为100，一部分气泡残留在壁面，直径为61，残留气泡作为下一个气泡生长的气泡核。

3.3 不同有限热源长度下壁面接触角对气泡生长脱离的影响

由图9(a)可以看出，气泡脱离直径随着壁面三相接触角的增大而增大，即由亲水表面转变成疏水表面，气泡脱离时间也逐渐加长。主要原因是三相接触角的增大，导致壁面张力增大，气泡脱离壁面需要更大的浮力克服壁面张力，因此在壁面需孕育更大直径气泡，生长时间变长，气泡脱离直径亦增加。故可通过减小壁面三相接触角，即改变表面亲疏性来使气泡脱离直径减小，缩短气泡从生成到脱离的时间，从而可以达到壁面强化传热。亲水壁面气泡脱离直径随着有限热源加热长度增加而增加，疏水壁面气泡脱离直径与有限热源长度无关。亲水壁面气泡脱离时间随着有限热源长度增加而减小，疏水壁面气泡脱离时间随着有限热源加热长度增加而小幅度减小。由图9(b)可知，亲水壁面有限热源长度增加，单位时间提供的热量增加，因此脱离直径增加，脱离时间减小。疏水壁面上覆盖一层气膜，有限热源长度增加对疏水表面气泡脱离直径影响不大，脱离时间小幅度减小。由此可以说明，通过调整有限热源的大小，可以改善壁面的换热效果。

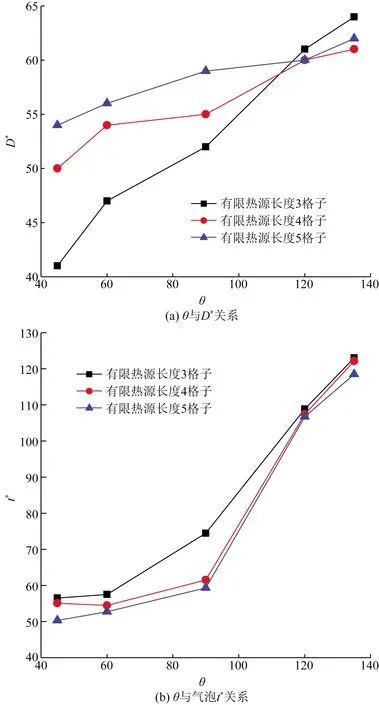
图9 不同有限热源长度下壁面接触角对气泡脱离的影响Fig.9 Influence of wall contact angle on bubble detachment under different finite heat source lengths

3.4 有限热源过热度对气泡脱离影响

图10为有限热源过热度对气泡生长脱离的影响。图10(a)为过热度与气泡脱离直径关系图，亲水壁面气泡脱离直径随着有限热源过热度升高而增大，表明气泡脱离直径与过热度成正比关系。由图10(a)中曲线可知，有限热源过热度升高，疏水壁面气泡脱离直径基本不变，这是由于疏水壁面气泡生长，气泡在中间断裂脱离主要受浮力、流场剪切力、气泡张力影响下，断裂脱离，故疏水表面过热度对气泡脱离直径影响不大，如图6(a)～图6(f)所示。

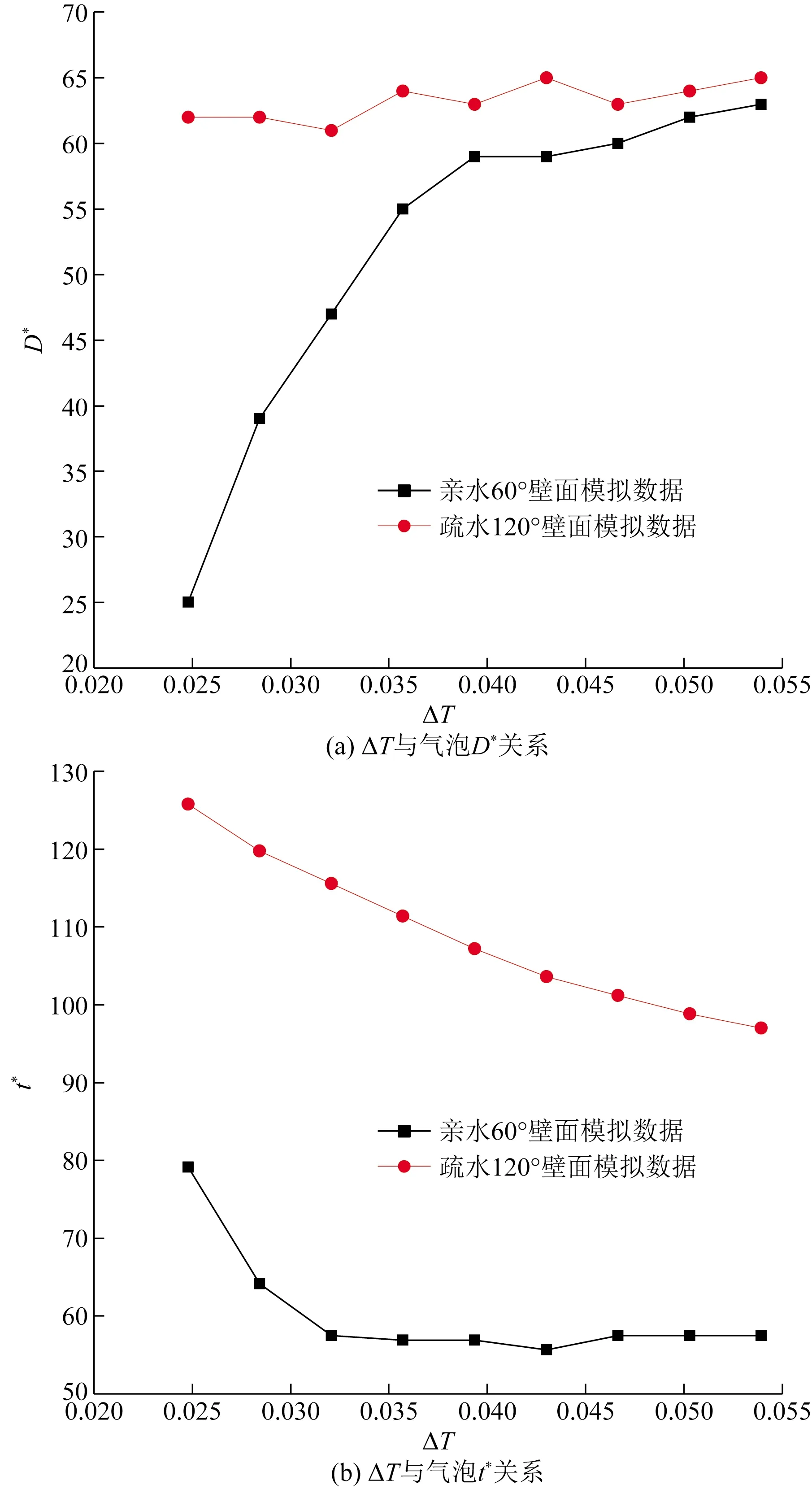
图10 有限热源过热度对气泡生长脱离影响Fig.10 Influence of superheat of heat source on bubble growth detachment

图10(b)为过热度对气泡脱离时间影响的曲线图，亲水壁面有限热源过热度的增加，导致气泡增长速度加快，因而气泡脱离时间减小。对于疏水壁面，气泡脱离时间随着过热度增加而大幅度减小，这是由于疏水表面在气泡形成初期先形成了一层气膜，但是随着过热度的增大，有限热源表面气膜传热能力增强，气泡的脱离时间将持续大幅度减小。

4 结论

在混和热Boltzmann方法基础上模拟了重力加速度对气泡脱离直径影响，分析了亲水壁面气泡的生长机理，得出以下结论。

(1)亲疏水壁面气泡生长机理不相同，亲水壁面气泡内部温度高，在惯性力的推动下长大，随后惯性力减弱，浮力增大，流体回流，气泡在浮力、流场剪切力，表面张力的作用下形成颈部直至脱离，壁面无气泡残留。疏水壁面气泡初始在惯性力与壁面张力下，沿壁面生长，随后惯性力减弱，浮力增强，气泡在流场剪切力与气液张力的拉扯下，在中间断裂脱离，壁面有大量气泡残留。

(2)在相同过热度下，亲疏水壁面都有快速生长、稳定生长、气泡脱离3个阶段，其中快速生长阶段气泡生长最快，稳定生长阶段气泡生长速度降低，脱离阶段气泡大小基本不变。疏水壁面较亲水壁面先产生气泡，疏水壁面气泡生长速度高于亲水壁面。

(3)气泡脱离直径随着壁面三相接触角的增大而增大，脱离时间随三相接触角增大而增大。亲水壁面气泡脱离直径随着有限热源加热长度增加而增加，疏水壁面气泡脱离直径几乎不随有限热源长度增加而改变。亲水壁面气泡脱离时间随着有限热源长度增加而减小，疏水壁面气泡脱离时间随着有限热源加热长度增加而小幅度减小。

(4)揭示了亲疏水壁面气泡脱离直径与过热度的关系，亲水壁面气泡脱离直径与过热度成正比，过热度的增加会使气泡生长速度加快，气泡脱离时间减小。疏水壁面过热度对气泡脱离直径影响不大，加热温度升高，传热推动力增强，气泡脱离直径基本不变，所以气泡脱离时间大幅度减小，疏水壁面气泡脱离时间明显大于亲水壁面，表明表面润湿特性对气泡脱离起主导作用，疏水性表面会增大汽泡的脱离阻力。