斜齿轮接触特性有限元分析

刘明勇， 屈阳*， 邓恩喜

(1.湖北工业大学农机工程研究设计院， 武汉 430068； 2. 湖北省农业机械工程研究设计院， 武汉 430068)

斜齿轮具有啮合性能好、重合度大、结构紧凑等特点，因而产生的冲击振动噪音较小，传动平稳，承载能力高，适用于高速重载的情况；研究斜齿轮的轮齿在一个完整的啮合周期内，齿面载荷分布和齿根处的应力分布以及变化情况，对研究齿轮裂纹以及疲劳寿命等有着至关重要作用，而有限元分析是解决此类问题的主要方法之一。

中外较多学者做了齿轮接触分析方面的研究。肖乾等[1]基于齿轮接触相关理论及轮齿摩擦关系，研究了齿面摩擦对齿轮接触特性的影响，发现齿面应力会随摩擦因数增加而增加。范舒阳[2]基于ANSYS软件建立斜齿轮接触模型并计算接触应力，将仿真结果与ADAMS编写的斜齿轮啮合程序结果对比分析，从而验证模型的准确性。朱才朝等[3]以齿轮实际工况为基础建立了精准的斜齿轮热弹耦合接触模型，研究了斜齿轮动态接触力、刚度以及温度场分布。李鹏阳等[4]结合软件与编程分析了接触表面温度分布及摩擦热对接触表面压力分布、表面米塞斯应力场及塑性应变的影响。Patil等[5]基于ANSYS软件结合有限元方法研究斜齿轮在静态条件下的接触应力，并考虑摩擦因数、螺旋角等因素对接触应力的影响，最后将仿真与理论分析计算结果对比分析，验证接触模型的正确性。Zhou等[6]根据齿轮接触面摩擦因数与齿根应力之间的映射关系，结合弯曲应力的数值仿真和试验测试，提出一种基于计算反求技术的齿轮摩擦系数预测方法。

王靖岳等[7]研究了齿面摩擦对齿轮传动特性的影响。吕中和等[8]基于有限元法建立了齿轮接触模型研究了齿根应力分布，并通过实验验证了仿真结果。Pedrero等[9]提出了一种基于最小弹性势能准则的沿接触线的载荷分布不均匀模型，并将模型计算出的齿轮弯曲应力和接触力与弹性线性理论(Navier方程)和赫兹接触模型对比分析。陈龙等[10]将直齿圆柱齿轮简化为平面模型建立齿轮接触分析模型，并结合几何分析(isogeometric analysis，IGA)方法研究了齿面接触载荷分布。周明刚等[11]对直齿圆柱齿轮传动啮合特性进行有限元接触分析，研究了热弹耦合、不同摩擦因数对齿轮接触压力的影响。Jabbour等[12]通过考虑载荷沿齿轮接触线分布特点，分析直齿轮、斜齿轮接触应力沿接触线分布规律。丁洁瑾[13]基于ANSYS研究了煤矿机齿轮在不同工况下的轮齿变形以及接触应力变化。唐进元等[14]基于动态接触理论，研究了齿面接触载荷分布。陆凤霞等[15]提出一种新的基于斜齿轮啮合特性的有限元网格划分方法建立轮齿接触分析模型，计算了啮合刚度、齿面变形及齿面载荷分布。

然而目前并没有学者系统地研究材料的塑性变形、齿面摩擦、接触表面的温度以及线性强化等因素对齿面接触力的影响，但这些因素却对接触特性分析有不可忽略的影响；应用有限元方法对斜齿轮接触分析，考虑以上因素对轮齿接触载荷分布的影响，最后通过实验与仿真计算对比分析，从而验证仿真模型的正确性。

1 斜齿轮三维建模

由基本渐开线方程与齿轮加工坐标系中的渐开线相结合，可得到斜齿轮在加工中的渐开线曲线方程[16-17]为

(1)

式(1)中：rb为基圆半径；αk为渐开线上任意点k的压力角；z为齿数；α为压力角；inv()为渐开线函数。

加工斜齿轮的齿条形刀具齿廓如图1所示，加工出齿根过渡曲线的齿条型刀具齿廓参数关系[17]表达式为

图1 加工齿轮齿廓参数Fig.1 Processing gear tooth profile parameters

(2)

式(2)中：r′为加工齿轮齿根圆角半径；n为圆心O′到中线的距离；m为圆心O′到中心线的距离；mn为法面模数；cx为径向变位系数；αn为法向压力角；ha为法向齿顶高系数。

刀具加工齿轮的齿根曲线如图2所示。根据渐开线方程与齿廓参数，可得到齿根过渡曲的参数方程[17]为

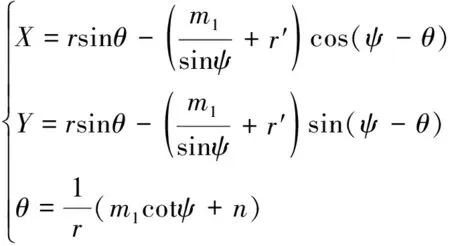
(3)

式(3)中：ψ为LL与刀具加工节线是夹角；θ为辅助变量。斜齿轮的基本几何参数如表1所示。

根据上述加工齿轮的齿廓曲线和齿根曲线以及斜齿轮相关参数，导入Solidworks中完成斜齿轮的三维建模，如图3所示。

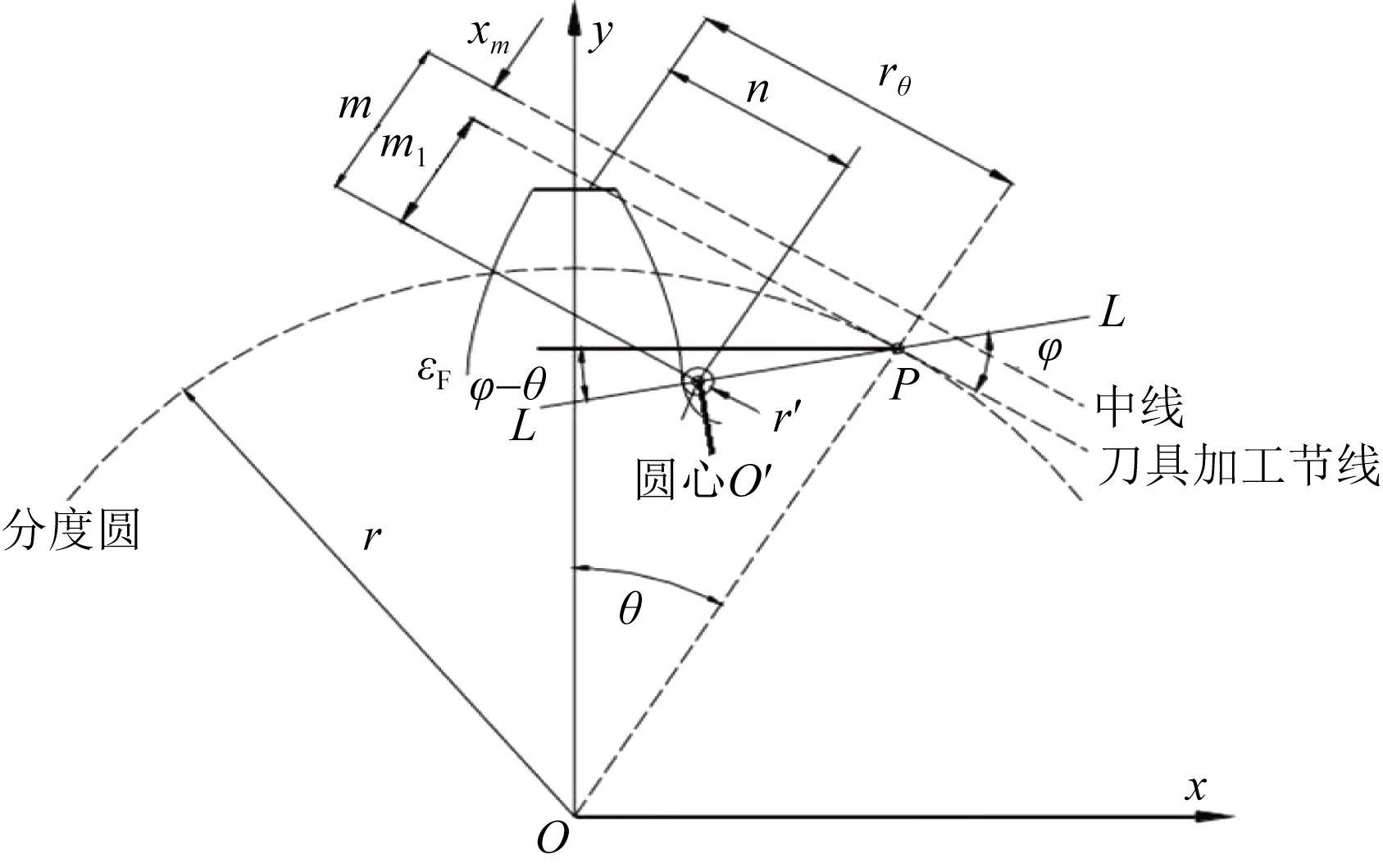
LL为刀具圆角与过渡曲线接触点的公法线；m1为圆心O′到刀具加工节线之间的距离；r为分度圆半径；P为啮合节点；rθ为节点P到中线的距离；xm为中线与刀具加工节线之间的距离；φ为 LL与刀具加工节线之间的夹角图2 刀具加工齿轮的齿根曲线Fig.2 Total root curve of tool processing gear

表1 斜齿轮几何模型基本参数Table 1 Basic parameters of the slope gear geometric model

图3 斜齿轮啮合的几何模型Fig.3 Geometric model of the slope gear meshing

2 轮齿接触分析

2.1 弹性模型接触分析

输入两种不同的应变曲线即可得到弹性以及弹塑性模型。其中，弹性模型只需添加线弹性应变曲线，而弹塑性模型仅需加入屈服强度(其他参数与弹性模型保持相同)，随后输入图4中曲线①即可。

若材料未达到屈服强度，曲线②则表现成线弹性关系，应力超过屈服强度(σs=387 MPa)则为线性强化关系，在设置材料属性时添加图4中的曲线②：

σ为应力；σs为屈服强度；ε为应力应变；εs为应力达到屈服强 度所对应的应变；E1为材料强化模量图4 塑性应变曲线和线性强化弹塑性应变曲线Fig.4 Plastic strain curve and Linear- reinforced elastic-plastic strain curve

斜直线近似模拟不同强化程度的应力应变关系，这样就可以得到线性强化弹塑性模型，即

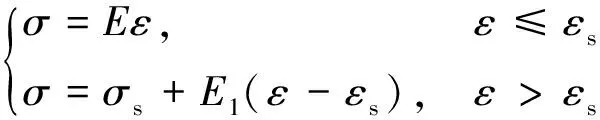
(4)

当E1=0时，即为理想弹塑性模型。

(1)齿轮端面对流换热系数。

(5)

式(5)中：vf为润滑油的运动黏度；λ为热传导率；rc为齿面上接触点半径；ω为齿轮角速度；Nμ为努赛尔指数；Pr为普朗特指数；j为指数常数；取j=2[3]。

(2)齿轮轮齿啮合面对流换热系数。

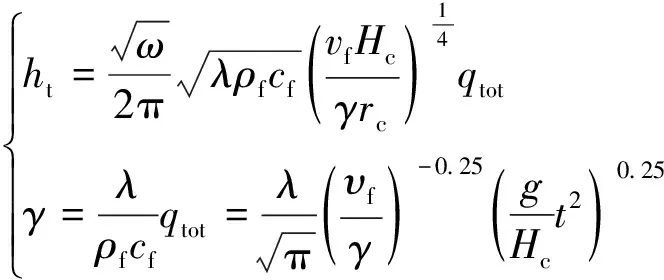
(6)

式(6)中：Hc为任意接触点位置轮齿的高度；ρf、υf分别为润滑油的密度、润滑油的运动黏度；cf、λ分别为润滑油比热、热传导率；γ为热扩散系数；qtot为标准化总冷却量[3]；g为离心加速度；t为抛射过程总时间。

(3)齿轮摩擦热流密度。

主、从动轮的接触齿面平均热流密度为Q1和Q2，分别表示为

(7)

式(7)中：βs为摩擦热流密度分配因子；η为摩擦能转换为热能的系数；f为摩擦因数；vgc为主动轮啮合线接触点相对滑动速度；pnc为平均接触压力；t1h为主动轮接触区摩擦热流密度通过接触宽度的时间；t1为主动轮啮合一周的时间[3]。

对啮合的接触齿面施加热流密度，齿顶面、齿根面、齿轮端面分别施加对流换热系数[18]，齿顶面、齿根面的对流换热系数可以等效为齿轮啮合面对流换热系数的1/3[19]，温度场施加载荷边界条件如图5所示。

为了减小计算量，故截取大小齿轮的6个齿啮合，对主动轮的4个轮齿研究分析；网格单元选用6面体C38R进行网格划分，对轮齿接触面以及齿根位置做网格加密处理。现对从动轮施加角速度ω=0.55 r/s，主动轮施加转矩T=1 500 N·m，如图5所示。

由图6可知，斜齿轮传动中接触齿面一直呈现着二齿-三齿-二齿的相互交替啮合的状态，其中图6(a)为二齿啮合；图6(b)为3齿开始进入啮合，二齿啮合转变成三齿啮合；图6(c)为1齿结束啮合，三齿啮合转换为二齿；图6(d)为4齿开始进入啮合，二齿啮合转换为三齿啮合。

图5 斜齿轮的接触有限元模型Fig.5 Contact finite element model of the slope gear

图6 主动轮啮合线变化过程Fig.6 Change process of active wheel engagement line

斜齿轮在啮合传动过程中，齿面接触载荷始终是沿着螺旋线方向移动分布，齿面接触载荷由齿根逐渐向齿顶方向移动。因为轮齿在啮合过程中二齿、三齿啮合不断交替的出现，故接触线长度也不断变化，从而使得轮齿上的接触载荷随齿轮啮合位置发生相应的变化。由仿真计算的接触总力约为42 111.7 N，而理论计算的数值约为42 597.5 N，仿真与理论计算的结果误差值为1.14%，从而验证了仿真接触模型建立的正确性。

2.2 塑性变形的影响

基于弹塑性模型，考虑不同载荷(400、1 000、1 500、2 000 N·m)下的齿面接触力，如图7所示。

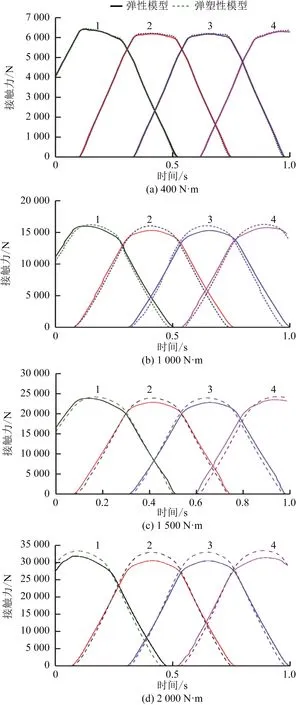
图7 不同工况下弹性以及弹塑性模型齿面接触力对比Fig.7 Comparison of elasticity and elastic model tooth surface contact force under different conditions

由图7可明显观察到：当考虑材料塑性参数后，在接触线处于稳定长度(接触载荷平稳)阶段，接触目标齿面的接触力均大于相同工况下弹性模型的齿面接触力，而弹塑性模型齿面接触力相比弹性模型分别增加了约为0.11%、1.84%、2.01%、3.13%，且扭矩越大，差值越明显。如图5所示，将主动轮2齿沿x-y截面切开，提取节点在1 500 N·m载荷下沿x-y截面上次表面应力变化如图8所示。

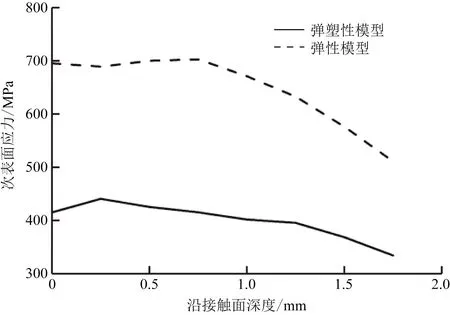
图8 x-y截面次表面应力随深度变化规律Fig.8 x-y cross section surface stress with depth changes

在一定的深度范围内，弹性模型的次表面应力始终大于弹塑性模型，且两模型次表面应力会随深度增加而减小，弹塑性模型应力减小的速率低于弹性模型；因为材料受载后会产生塑性变形，在此过程中，外载荷的一部分能量转换成了材料微观晶粒间的势能，且此势能会转换成塑性变形而存在材料体内，由此而产生残余应力，故随着载荷的增大，应力也会持续增加。为了研究次表面塑性变形的变化，分别提取了在同一时刻下4种工况下在x-y截面的塑性变形区域，如图9所示。

随着载荷的增大，塑性变形区域会逐渐扩大，且最大塑性变形区的面积也在增大，因为当齿轮受载其应力值达到屈服强度后，塑性变形会随载荷的增大而增加；因此考虑材料塑性参数对齿面接触特性有不可忽略的影响。

2.3 齿面摩擦的影响

齿轮啮合中的齿面摩擦因数f≤0.2，结合相关的研究以及本文斜齿轮的相关参数，故本次仿真计算的齿面摩擦因数在0.01～0.2选取[20]。在弹性模型中将齿面不考虑摩擦设置成摩擦接触的模型，研究2齿齿面在3个不同摩擦因数(0.05、0.10、0.15)下接触力的变化曲线如图10所示。

当接触线处于稳定长度时，摩擦因数越大，接触力就越大；当接触齿面存在摩擦，齿面摩擦状态为滑动摩擦，故接触面积会减小，因此，齿面接触力大于未考虑摩擦状况下的接触力。

图9 四种工况下弹塑性模型x-y截面塑性变形区域变化Fig.9 Changes of elastoplastic model x-y cross-section plastic deformation regions under four working conditions

图11(a)、图11(b)、图11(c)、图11(d)代表了4个摩擦因数下的齿根应力。可以看出，随着摩擦因数的增加，齿根应力也随之增大；由于齿轮啮合中齿面摩擦力会改变接触应力以及轮齿变形，因此齿根应力也随之变化，故齿面摩擦对轮齿接触载荷的影响不容忽略。

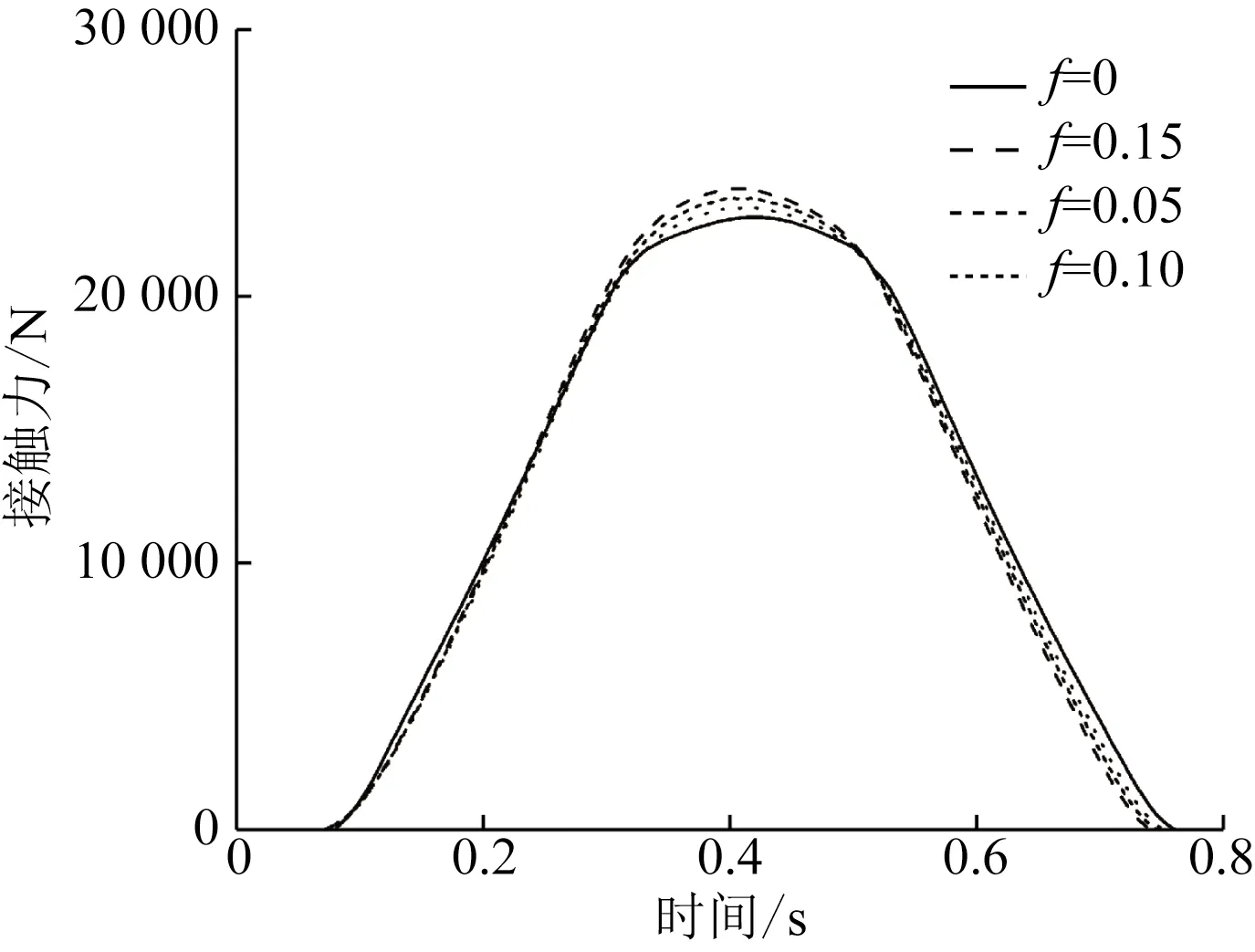
图10 不同摩擦因数对轮齿接触力的影响Fig.10 Effect of different friction coefficients on the contact force of the rotation tooth

2.4 温度的影响

为了研究温度对齿面接触力的影响，设置齿面摩擦因数为0.1，其他参数不变，扭矩为1 500 N·m的变化曲线如图12所示。

将轮齿间的摩擦热考虑到斜齿轮接触分析模型中后，齿轮齿面因相互接触摩擦从而产生热量，导致齿面温度升高；由于温度升高后，材料分子之间的平均动能会增大，使得分子之间发生相对的移动，致使分子间的相互作用力将减小，最终导致材料的屈服应力相对减少并接触压力也会随之减小；紧接着，材料就开始发生软化现象，则接触面积会逐渐扩大，故齿面接触力就会随之而减小。综上所述，考虑温度的齿面接触力的最大值低于不考虑温度的最大值；说明齿面接触温度对接触力会有一定的影响，但影响不明显。

齿面摩擦会使接触表面软化而导致接触面积增大，由于体内分子发生挤压以及温度传递到齿轮体内，使得次表面产生热应力，故出现了如图13中的一定的深度内考虑温度的次表面应力大于未考虑温度的，且两者的应力都会深度的增加而逐渐减小。为了研究对温度塑性变形的影响，图14(a)、图14(b)分别展示了不考虑温度和考虑温度的塑性区域。

图12 考虑温度场轮齿齿面接触载荷Fig.12 Considering the temperature field wheel tooth surface contact load

图13 x-y截面次表面应力分布规律Fig.13 x-y cross-sectional surface stress distribution

考虑温度塑性变形区域中心的扩展方向发生偏移，这是由于次表面温度分布的不均匀使次表面应力扭曲变形；一定深度内，考虑温度的应力高于不考虑温度，故其所对应的塑性变形的面积也会相应增大。

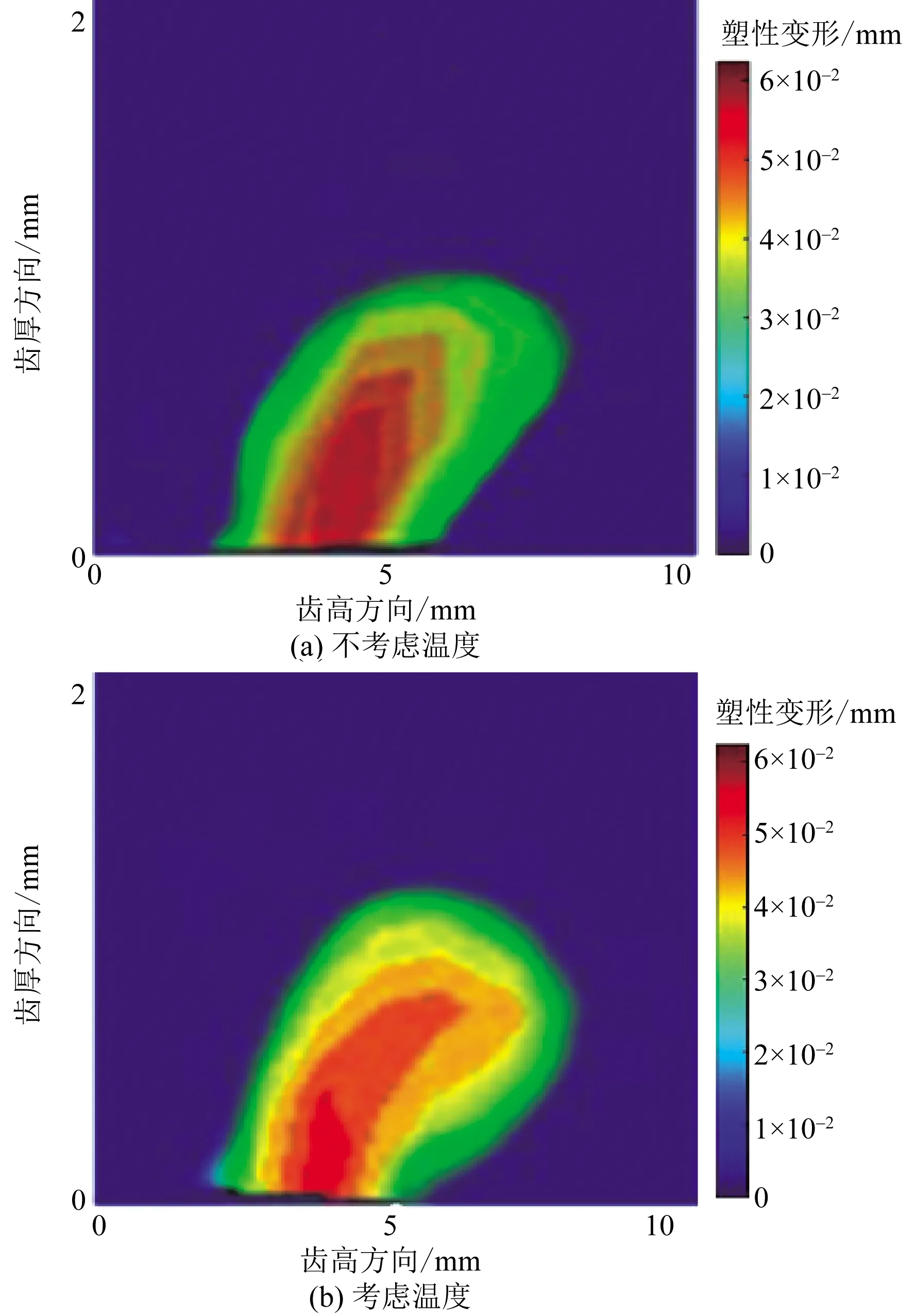
图14 x-y截面塑性变形区域分布Fig.14 x-y cross-sectional plastic deformation region distribution

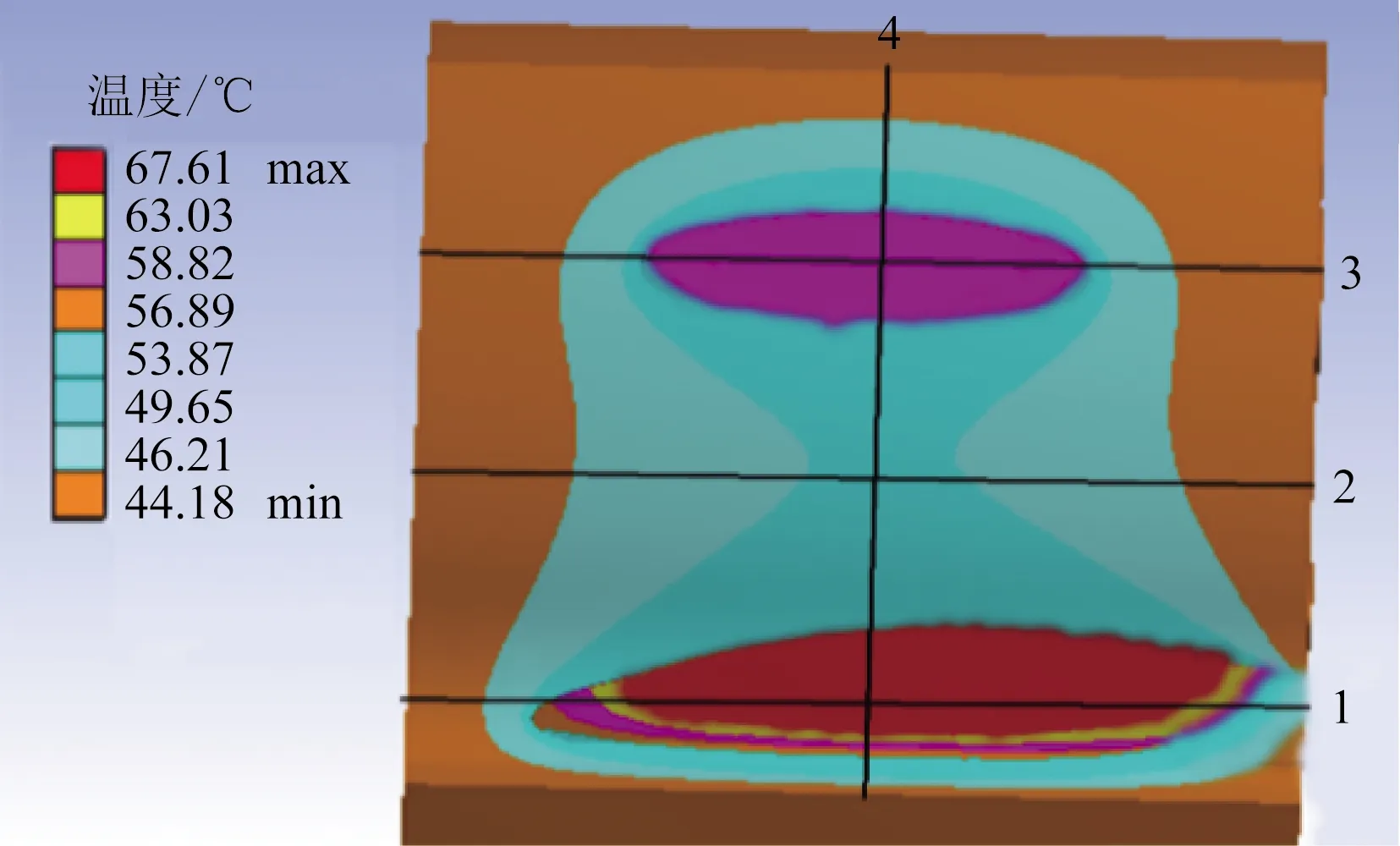
图15 主动轮2齿面温度场云图Fig.15 Active wheel 2 tooth surface temperature field cloud map

图15展示了主动轮2齿面温度场分布，并分别沿齿高和齿宽方向提取了4条路径的温度变化曲线。由图知接触面最高温度为67.61 ℃左右，靠近齿根处；次高温度为58.82 ℃，靠近齿顶处；由于二齿啮合和三齿啮合交替处的相对滑动速度较大，而摩擦产生的热流通量和相对滑动速度成正相关，故轮齿啮合交替时热流通量增加[3]，所以接触齿面出现两个局部温度峰值区域。由路线 1、2、3可知，沿齿宽方向温度场中间温度高，两端面温度低，因齿轮端面与润滑油混合物对流散热所致[18]。

2.5 线性强化的影响

为了研究3种不同线性强化模型(即在材料硬化的程度E1分别为0、1%、3%E，E为弹性模量)在不同工况下接触表面的应力的变化情况，提取主动轮2齿表面最大应力，如图16所示。

在未达到屈服应力前，3种模型的硬化程度不同，故线弹性应变曲线并不保持一致；在一定扭矩范围内E1=0的应力明显大于E1=1%E和E1=3%E模型，因为其材料硬化程度低于其他两种模型，故变形最大即应力最大；当达到屈服应力后，E1=0模型的应力不大于其他两种，因为其为理想弹塑性模型，应力不会随载荷增大作用而变形逐渐增加而变化了。当扭矩达到1 700 N·m时 两种模型应力值达到一致，由于材料硬化程度不同故在相同载荷下E1=3%E变形小于E1=1%E；当扭矩小于1 700 N·m，E1=3%E的应力低于E1=1%E；当扭矩达到1 700 N·m后，两种模型的应力值已高于屈服应力，E1=3%E强化阶段斜直线的斜率大于E1=1%E，故其应力变化速率大于E1=1%E，因此其应力高于E1=1%E。

选取1 000 N·m工况下3种强化模型中主动轮2齿沿x-y截面上同一节点次表面应力以及对应的塑性变形变化如图17所示。

图16 不同强化模型的次表面最大应力变化规律Fig.16 Differential stress changes in the secondary surface of different strengthening models

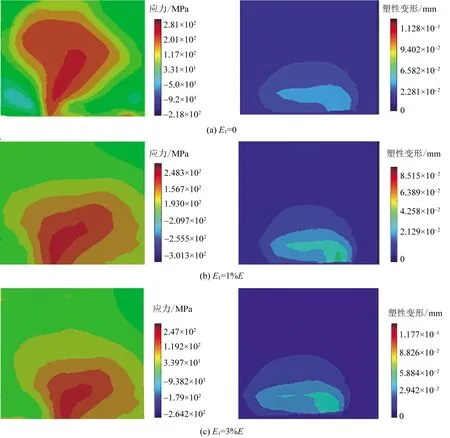
图17 次表面应力以及次表面塑性变形Fig.17 Surface stress and surface plastic deformation

E1=1%E模型的次表面应力明显小于其他两种模型，但其对应的塑性变形量却最大；因为当应力大于屈服应力后，同一应力下，塑性变形量会随线性强化的增加而减小。综上可知，不同工况下材料强化的参数选择对接触应力的影响各不相同，故做理论研究时应选用更符合实际工况的材料强化模型。

3 实验验证

实验采用MCL-1A齿轮磨损试验机进行实验，其由主轴电机驱动，通过驱动齿轮箱、弹性轴、试验齿轮箱共同作用对实验齿轮施加转速；在主控台设置实验扭矩目标值，其由加载离合器添加，扭矩数值通过(动态)扭矩传感器在主控台中显示，达到目标值即可停止加载；随后，在主控台中设置转速以及运行时间，点击发送即可开始试验。图18(a)为MCL-1A的原理图，图18(b)为MCL-1A的现场实物图。

3.1 温升测试实验

齿轮啮合过程中由于接触齿面摩擦产生温度，则会影响接触载荷分布；本次试验通过电偶温度传感器将温度传输到多温度巡检仪上进行实时监测，测试现场图如图18(c)所示。为了模拟准静态工况，设定齿轮转速为33 r/min，取不同工况下测量区域中温度；为了减小实验误差，先让试验台以给定转速运行一段时间达到热平衡后开始实验并测量。

图19所示为不同扭矩下仿真与实验的温升分布曲线，齿根以及齿顶接触区域的仿真与实验结果均取的是温度平均值；由于不同位置的散热效果不同，且齿轮啮合过程中齿面润滑油入油分布不一致，导致冷却效果不均匀，故齿顶和齿根处的温度分布不同；由于实验中齿顶测量区域处于齿顶圆附近，润滑效果比较差，而齿根测量区域接近于齿根圆附近，接触面积较小，散热效果好，故其温度会小于齿顶处。因为温度场仿真为理想环境，而实验中由于环境温度的差异以及齿轮自身散热等因素，导致实验结果均低于仿真结果；且温度随载荷的增大而升高，但实验与仿真温度变化趋势基本相同，其相对误差也在可接受范围内，说明了仿真模型的正确性。

1为主轴电机；2为驱动齿轮箱；3为(动态)扭矩传感器；4为弹性 轴；5为加载离合器；6为试验齿轮箱；7为实验齿轮图18 实验图Fig.18 Experimental map

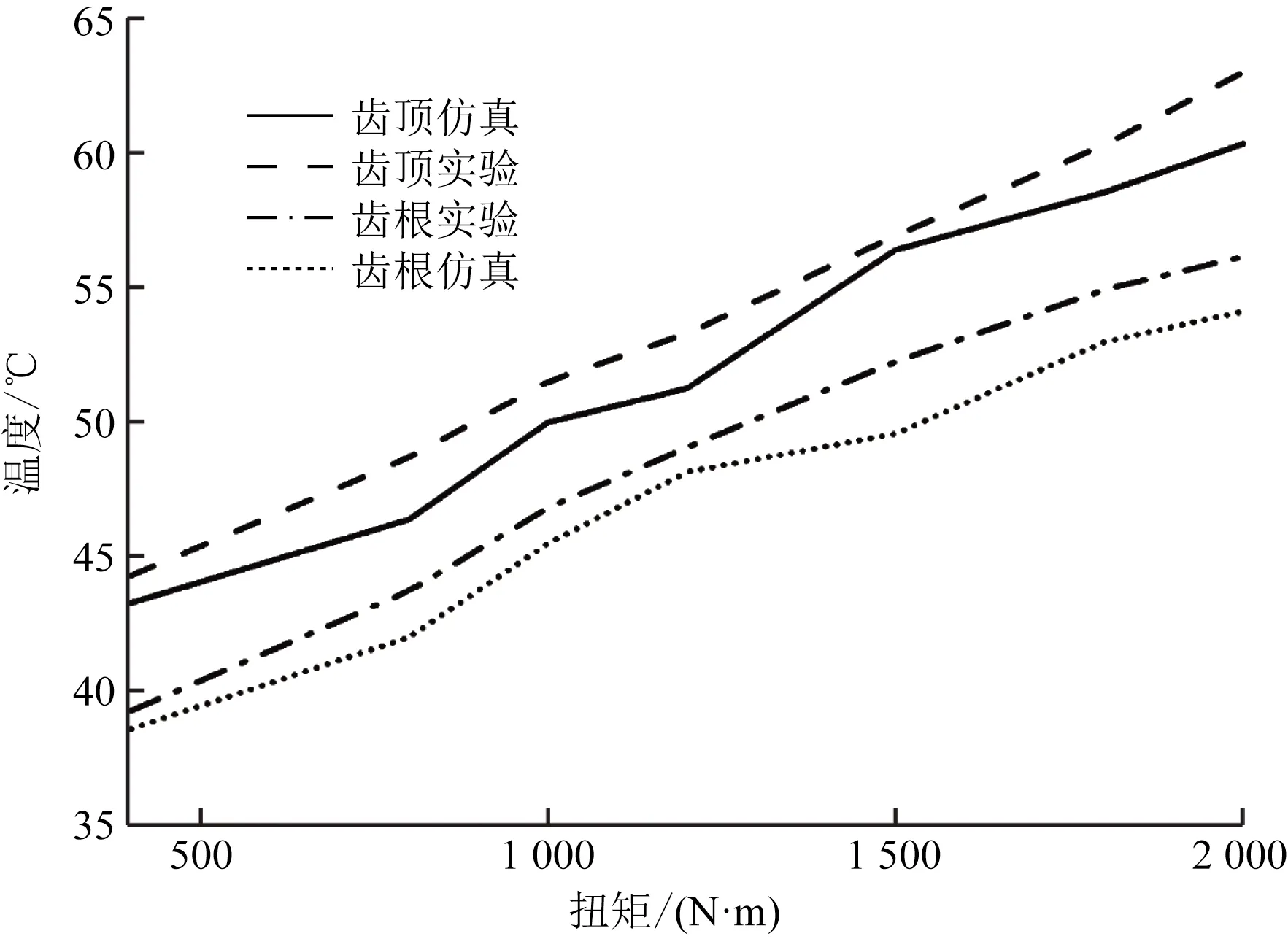
图19 齿根齿顶表面区域温升结果对比Fig.19 Comparison of temperature rise results in the surface of the root tooth

3.2 应变测试实验

为了研究齿根弯曲应力，试验将在3种工况下进行测量，转速均为33 r/min，加载扭矩分别为600、800、1 500 N·m，分别为工况1、工况2、工况3，测试现场图如图18(d)所示。将实验结果与仿真结果相比较，计算相对误差，验证仿真模型；由于实验台的输入扭矩存在一定的偏差，受到安装误差、齿形误差、传动误差以及啮合冲击等影响，故实验结果会存在误差。

由于被测齿轮受到前对齿啮出冲击和后对齿的啮入冲击产生挤压，因此图20的弯曲应力出现先凸后凹的变化趋势；最大拉应力出现在双齿啮合位置附近，其他区域应变值基本趋于零，因为被测齿轮退出了啮合而不受载荷。

图20 3个工况下一个周期内仿真与实验弯曲 应力结果对比Fig.20 Comparison of simulation and experimental bending stress results in three working conditions

由于实验中应变测试中取点频率与仿真计算设置时间步数不同，以及应变片贴片的位置和仿真提取节点位置会存在一定的偏差，因此仿真和实验中轮齿啮合周期会不同，所以两种最大弯曲应力不会出现在同一时刻，但其变化曲线趋于相同，说明仿真以及实验中齿轮的受载状态是一致的。

将仿真与实验中的最大弯曲应力结果比较如表2所示。3种工况下的实验结果都略大于仿真结果，但实验应力值相对仿真应力值的误差均不超过20%，说明实验结果在理想范围内，验证了上述接触模型的准确性。

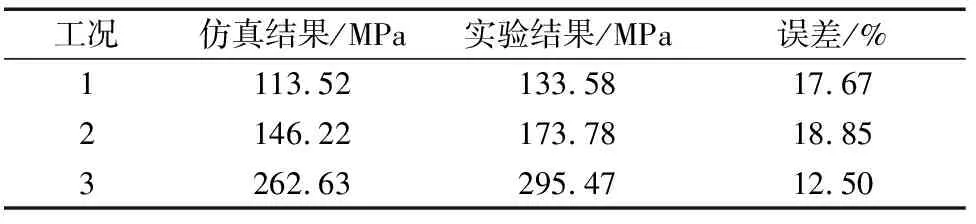
表2 仿真与实验最大弯曲应力Table 2 Simulation and experimental maximum bending stress

4 结论

建立了斜齿轮三维模型，用有限元法对齿轮做接触分析，研究了塑性变形、齿面摩擦、温度以及材料线性强化等因素对接触特性的影响，最后通过试验将实验结果与仿真结果分析对比，验证了仿真模型；并得出以下相关结论。

(1)在4种载荷(400、1 000、1 500、2 000 N·m)下弹塑性模型的齿面接触力在接触线长度稳定时刻，相比弹性模型分别增加了约0.11%、1.84%、2.01%、3.13%，载荷越大效果越明显；在一定的次表面深度范围内，弹塑性模型的应力始终不大于弹塑性模型，但随着深度增加，其减小的速率小弹性模型，且次表面的塑性变形面积会随载荷的增加而扩大。

(2)考虑齿面摩擦后，在接触线稳定长度阶段，齿面接触力大于不考虑摩擦因数齿面接触力；且摩擦因数越大，齿根应力就越大。

(3)考虑齿面温度对接触载荷的影响后，考虑温度的齿面接触力最大值将小于不考虑温度的接触力；说明温度对齿面接触力分布有一定影响。

(4)在不同载荷范围内的三种强化模型的表面最大应力变化趋势不同，故次表面的应力和塑性变形也各不相同；说明选择合适的材料强化程度对接触面应力有重要影响。

(5)通过温升实验可知，由于齿顶处的散热效果差，故实验和仿真中齿顶区域温度高于齿根区域，并且实验结果均低于仿真结果，但变化趋势保持一致，说明了仿真模型的可靠性；应变测试中齿根弯曲应力同仿真曲线变化趋势基本一致，两者的最大弯曲应力相对误差值低于20%在可接受的范围内，从而验证了仿真模型的准确性。