基于耐久性能的混凝土寿命预测方法研究进展

孟乔， 黄维蓉

(1.重庆交通大学土木工程学院， 重庆 400041； 2. 重庆交通大学材料科学与工程学院， 重庆 400041)

混凝土是中国建设工程中最主要的结构材料，其结构耐久性在《混凝土结构耐久性设计规范》(GB/T 50746—2019)中定义为“在设计确定的环境作用和维修、使用条件下，结构构件在设计使用年限内保持其适用性和安全性的能力”，说明耐久性对工程寿命至关重要。为了缓和日益提升的人民需要和服役时间不足的基础建设之间的矛盾，保证结构安全性，需要对混凝土结构耐久性问题进行深入研究。目前提升混凝土耐久性的途径主要有两种：一是降低其性能退化速率；二是提升结构初始性能[1]。然而，建筑物各组成结构随时间推移寿命各不相同，控制其性能退化速率难度较大；且现有技术下建设的大型基础建设设计年限超过100年甚至更久，仅通过提升初始性能保证结构安全同样难以实现。因而，混凝土寿命预估在结构设计中就变得十分重要。中外学者对混凝土寿命预估主要还是基于疲劳试验，以长时间荷载应力与疲劳寿命建立的数据规律，推演寿命预测公式。但该种方法耗时耗力，需要大量经费支持，且针对性较强，不具有普适性，同时所得推演公式能否应用于已出现病害的混凝土结构还未可知。因此，通过建立预测方法和模型对混凝土进行寿命预估是十分必要的。

国外对可靠性问题的研究始于20世纪70年代初期，首次将可靠度的概念引入柔性路面设计系统中。80年代，Witczak将可靠度计算结果绘制的诺模图引入路面结构设计，开启了路面设计可靠性新观念[2]。在此之后，美国国家公路与运输协会(American Association of State Highway and Yransportation Officials，AASHTO)将可靠性概念与相关系数引入设计指南中[3]。在相关技术标准要求的框架下，基于混凝土耐久性进行寿命预测成为混凝土结构设计主要参数之一[4]。Possa等[5]应用马尔可夫链预测混凝土结构从钢筋腐蚀开始的服役寿命，结果误差在可接受范围内，Foraboschi[6]提出多尺度纤维加固混凝土构件寿命预测模型，通过其封闭的形式解，预估外部钢筋寿命。Srubar[7]基于概率分析预测普通骨料和再生骨料混凝土发生锈蚀的时间，Baroghel-Bouny[4]采用有效氯离子扩散系数和液态水渗透特性预测混凝土寿命，并对比直接实验法，基于简单解析公式的间接法和涉及物理模型的数值分析法预测结果。Andrade等[8]通过菲克第二定律预测氯离子在混凝土结构中的渗透作用，从而预测混凝土在海水环境下的服役寿命。Lee等[9]采用确定性和概率模型方法，根据混凝土碳化模型预测其服役寿命，发现确定性和概率性模型结果相近。

中国在相关问题的研究上起步较晚，20世纪80年代后期首次将可靠性概念引入路面结构设计中。随后，Zhang等[10]采用两参数威布尔分布对路面疲劳寿命进行假定，并在结构设计方法中引入可靠度系数。谈至明等[11]基于张国栋等的研究基础提出降次积分法，对研究进行充实和完善。随后，可靠性概念被引入重要结构设计中。王立久等[12]以抗折强度的衰变过程模拟混凝土结构老化，并建立耐久寿命预测模型。牛荻涛等[13]通过混凝土构件强度等深入了解铁路桥服役情况，并预测其剩余寿命，武利强等[14]从环境、材料、构建及结构4个层次预测混凝土在氯盐环境下的寿命分布，关虓等[15]采用概率统计方法，以混凝土碳化情况评估结构寿命。毛江鸿等[16]采用双向电渗技术，基于菲克第二定律进行数值求解预测。陆春华等[17]基于氯离子扩散和裂缝宽度模型，以蒙特卡洛抽样方法建立失效概率与可靠度指标之间的关系。魏保立等[18]提出利用车辆-路面耦合振动的随机功率谱密度函数来预测路面的疲劳寿命，未知量少，认可度高。高升[19]对现有混凝土耐久性寿命预测方法进行分类，并对比多种模型的优缺点。蒋琼明等[20-21]着重研究了粉煤灰掺量对扩散系数的影响，随粉煤灰掺量增加，混凝土与氯离子的远期结合能力有所下降，且随着服役时间的增长呈现衰减趋势。吴憾[22]基于高精度反向传播(back propagation，BP)神经网络，建立氯离子侵蚀下混凝土结构寿命预测模型，分析各参数对混凝土结构寿命的影响。陈宣东等[23]采用蒙特卡洛方法建立钢筋混凝土耐久性失效模型，为后期结构监测及修复提供理论支撑。路承功等[24]选择威布尔分布对钢筋混凝土的可靠性进行评价，通过分析钢筋混凝土在盐腐蚀环境下的寿命，证明结构可靠性。彭艳周等[25]针对北方海洋冻融循环和氯离子侵蚀的耦合影响，基于菲克第二定律进行结构锈蚀寿命预测。Yang等[26]基于冻融损伤理论，优化和改善了威布尔分布模型，通过工程实例验证了方法的可行性。

过去50年间，中外学者基于混凝土耐久性能提出如经验估计、数值模拟、降次积分、菲克第二定律、灰色理论、概率分析、数学模型和齐次马尔可夫链等多种方法对混凝土寿命进行预测，其中不乏有些方法所得结果与实际情况偏差较大。例如，菲克第二定律需要假定混凝土是半无限介质，且该模型对环境因素变化十分敏感，适应性较差；经验估计是通过现有专家多年的经验积累来预测混凝土的寿命，主观依赖性较强，局限性明显；而灰色理论模型因无法完全了解起内部耦合情况，预测结果的准确性也有待商榷。

综上可知，基于耐久性能的混凝土寿命预测的关键是选择适宜的方法，合理模拟实际环境，才能得到与真实结果误差较小的预测值。而现有文献一般仅针对某一环境因素或条件提出一个模型，未曾讨论模型的可推广性和适用范围，在研究者选取模型的时候存在障碍。因此，现将分别介绍基于耐久性能下的结构混凝土、道路混凝土和海工混凝土的多种寿命预估模型，对不同服役环境下的混凝土可靠性计算提供指导意义。

1 结构混凝土

1.1 碳化

结构混凝土一般情况下与大气环境直接接触，其耐久性问题主要来源于空气中二氧化碳和水结合引起的混凝土碳化，其实质为混凝土的中性化反应，主要化学反应式为

碳化导致混凝土内部碱性降低，钢筋钝化膜破坏，结构承载力下降，结构寿命受到影响[27]。碳化问题是混凝土钢筋锈蚀的前提条件，一般以混凝土碳化导致钢筋锈蚀作为结构寿命终结的标志[13]。结构混凝土一般用于建筑物的关键部位，对建筑物使用寿命影响巨大，因而研究混凝土碳化及其寿命预测模型具有重要意义。故将基于碳化深度和钢筋锈蚀状态两个方面对结构混凝土寿命进行预测。

牛荻涛[28]最先提出混凝土碳化深度的随机过程模型为

(1)

式(1)中：X为混凝土碳化深度，为随机过程；t为混凝土碳化时间；k为碳化深度影响系数。

该模型虽然简单明了，但碳化深度影响系数为定值，无法研究变化的配合比设计和服役环境对混凝土碳化深度的影响，不同地域下参数k的取值也应有所区别，更无法适应多因素耦合作用下混凝土碳化深度的研究。李英民等[29]在牛荻涛[28]提出的模型中添加应力水平与水灰比影响系数，更好贴近实际情况，能够更准确评价混凝土碳化过程，但其适用性仍较差，无法有效拟合当下混凝土复杂的服役环境，预测结果与实际相差较大。

邸小云等[30]提出混凝土结构因碳化导致钢筋锈蚀深度与时间之间的关系，并给出从钢筋出现锈蚀到混凝土出现锈胀裂缝的预测模型为

(2)

式(2)中：Tb为混凝土保护层开裂前钢筋锈蚀时间；λe1为混凝土保护层锈胀开裂前的钢筋锈蚀速度;δcr为混凝土保护层锈胀开裂时刻的钢筋锈蚀深度。

此模型成立的前提是基于钢筋锈蚀速率与深度之间为线性关系，若不满足此前提，该模型结果误差较大，因而适用性受到限制。

基于碳化深度与保护层厚度的关系，混凝土碳化寿命准则[13， 15， 27]可以表示为

Ωc={c-x0-X(t)≥0}

(3)

式(3)中：c为混凝土保护层厚度，服从正态分布；x0为碳化残量；X(t)为混凝土碳化深度；Ωc为混凝土碳化寿命准则。

根据碳化寿命准则，关虓等[15]提出混凝土劣化准则为

Z(t)=c-Δck-x(t)<0

(4)

式(4)中：Z(t)为混凝土劣化失效准则；c为混凝土保护层厚度；Δck为混凝土碳化残量；x(t)为混凝土碳化深度；对于一般大气环境，不考虑随机性的前提下，取碳化安全残量Δck为10 mm。

式(3)和式(4)的重点在碳化残量的取值，其本身与保护层厚度、抗压强度及环境相对湿度有关，可以较好拟合不同环境及工程的特殊性。但实测碳化残量会对结构造成损伤，损伤后结构的寿命与损伤前有较大差异，且为了预测寿命而破坏混凝土结构，造成耐久性降低，可谓因小失大。

1.2 酸雨

结构混凝土大多应用于室外，近年来因化石燃料燃烧向大气排放大量硫、氮等酸性物质，雨、雪在形成和降落过程中与之结合，形成了酸雨，导致非金属建筑材料(如混凝土等)表面硬化水泥溶解，出现空洞和裂缝，强度降低，从而对建筑物造成破坏。主要化学反应式为

张亚明[31]考虑酸雨侵蚀混凝土的多个性能指标，采用多变量灰色模型对其寿命进行预测，MGM(1，n)模型为n元一阶常微分方程组，即

(5)

多变量灰色模型MGM(1，n)是基于GM(1，1)改进得到的，该种模型可适用于研究多种环境因素耦合作用对混凝土碳化深度的影响。通过n元参数代表酸雨引起n个性能指标的变化，具有更高的预测精度，显示了该方法进行路基沉降预测的有效性。因而，在酸雨条件下采用多变量灰色模型预测混凝土寿命更为准确。但灰色模型的本质是差分计算，随着计算次数的迭代，误差将会越来越大，很难运用到混凝土长期寿命预测工作。

1.3 疲劳

混凝土在重复荷载作用下会产生裂缝，直至引起疲劳破坏，因而以疲劳寿命预测混凝土结构寿命的是一种合理的手段。Isojeh等[32]提出一种杆系分析法，在考虑混凝土应变积累的前提下研究混凝土强度退化及裂纹扩展情况。根据Paris裂纹扩展定律，依据应力强度因子范围(ΔK)、疲劳应力范围(Δσ)、裂纹尺寸(a)和形状因子(Y)对混凝土疲劳寿命进行预测，公式为

(6)

(7)

而Rodriguez等[33]提出混凝土裂缝宽度与耐久性关系的寿命预测模型为

(8)

式(8)中：Tc为混凝土裂缝宽度；wm为混凝土保护层锈胀裂缝最大宽度容许值；λe2为混凝土保护层锈胀开裂后的钢筋锈蚀速度。

以上两种模型成立的前提是裂缝均处于同一平面，若疲劳裂缝处于复杂曲面上，则这两种模型均不适用。复杂曲面上的裂缝可通过蒙特卡洛方法模拟抽取随机样，而后根据裂缝宽度预测混凝土寿命[34]。若随机变量数量较多时，可采用Evan[35]提出的拟Monte-Carlo法进行随机样抽取，但减少计算量的同时需考虑其对功能函数概率分布特征的依赖性。

除以上3种预测结构混凝土寿命的方法，相关寿命预测模型还有很多，如日本建筑学会基于估计使用寿命提出的因子法[36]，确定性和概率性方法[9]，以及基于破坏形式[6]对结构寿命的预测模型，通过定量分析预测结构混凝土的剩余寿命，对结构可靠性进行正确评估。

2 道路混凝土

道路用混凝土自浇筑至投入使用，体系存在温度应力、结构约束力和荷载应力等，会造成路面板横向开裂，即损伤萌生；随着道路服役年限的增长，裂缝进一步延伸，达到损伤稳定扩展状态；最终发展为结构性断裂破坏，造成混凝土路面寿命提前终结[37]。说明疲劳裂缝是混凝土结构寿命核心问题，目前混凝土疲劳破坏机理主要有3种：唯象理论、断裂力学和连续损伤力学[38]。

2.1 S-N曲线

18世纪中期，Wohler首次提出S-N曲线，并将其应用于结构寿命预测。80年代，Tepfers[39]通过拉伸试验得出混凝土单对数疲劳方程。宋玉普[40]、赵学峰[41]基于S-N曲线预估混凝土疲劳寿命，混凝土结构的S-N关系为

lgN=16.67-16.76Smax+5.17Smin

(9)

式(9)中：Smax和Smin分别为最大、最小应力水平；N为疲劳破坏时循环次数。

经过大量试验数据验证，《混凝土结构设计规范》(GB 50010—2010)对上述疲劳方程进行修正，得

lgN=16.51-16.60Smax+5.12Smin

(10)

徐庆元等[42]也基于式(10)对桥上CRTS Ⅱ型板式无砟道混凝土进行研究，对比式(10)和宋玉普的修正疲劳方程预测结果[40]发现，应力较低时，两者结果无显著差异，而应力较高时，前者误差较大。然而，基于S-N曲线预测的混凝土疲劳寿命也因材料本身离散型较大，对循环应力状态敏感，结果准确性有待商榷。为减小试验结果误差，量化混凝土寿命的不确定性，李希朋[43]、Tang等[44]采用室内小梁弯曲试验，固定循环应力，建立不同水平下的疲劳方程为

lgS=lga-blgN

(11)

采用疲劳方程预估混凝土寿命较为简便，参数少且易于测量。陈猛等[45]借助疲劳方程得到不同失效概率下的疲劳方程，发现lgS与lgN具有良好的线性关系。李东清[46]基于混凝土疲劳方程和损伤本构关系，建立隧道疲劳寿命预测方程。但是，当材料受到多级不同应力幅度循环加载时，该方法则不适用。

2.2 Paris公式

姚婵娟[47]基于Paris公式对不同尺寸下总应变能密度得到结构扩展寿命预测模型为

(12)

式(12)中：Np为不同裂纹尺寸时的扩展寿命；Wc为材料断裂时总塑性应变能密度；φ为裂纹尖端区域塑性应变能密度；a为每个循环过程中裂纹扩展距离；α0为每个循环工程中裂纹的初始距离。

Paris公式主要是建立裂缝深度与寿命之间的联系，但在实际操作过程中可知，测量裂缝深度是十分困难和难以施行的，很多大结构建筑物的裂缝深度更是难以通过探测的方式确定。因而，Paris公式的适用性也比较局限，仅适用于可测量裂缝的小结构建筑物。为了解决裂缝深度测量困难的问题，魏亚[48]通过四点弯曲试验，以有效裂缝长度取代裂缝扩展深度，采用断裂韧性及临界裂缝张开位移预测存在裂缝的混凝土板疲劳寿命，两参数表达式为

(13)

(14)

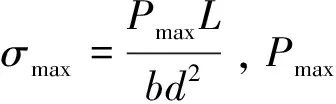
2.3 能量耗散方法

Lei等[38]采用能量法分析混凝土在加载过程中的能量耗散，并认为损伤导致的能量耗散与总能量应趋于一致，以疲劳荷载下能量耗散的演化规律预测混凝土的疲劳寿命函数为

(15)

式(15)中：Nf为疲劳寿命；Wd为累计耗散能量；Wdc为临界耗散能量。

该模型测量能量耗散需破坏结构，无法应用于已建造构筑物，若采用室内试验，需建立室内与实际之间的换算系数，所以适用范围大大减小。

除了以上3种代表性方法，也可采用室内外结构劣化速率比得到的加速系数[49]、基于能量损伤的连续损伤理论[50]、通过降次积分法和干涉理论计算的结构理论可靠度分析[51]等方法准确预测混凝土道路的结构寿命，尤其是采用不同水平下的疲劳方程和四点弯曲试验来作为预测方法，对结构在服役期内的安全具有潜在意义。

3 海工混凝土

海工混凝土因其特殊位置，长期受到海洋生物、盐类、水、温度等因素影响，易造成结构破坏，缩短其服役寿命。针对海洋环境特点，武利强等[14]基于水位将海工混凝土结构划分为水下区、潮差区、浪溅区和大气区四类，分别对应盐类腐蚀、冻融循环、冲击磨损和碳化作用四类影响因素。因其服役环境的恶劣，海工混凝土的抗腐蚀性能要求较为严苛。通过预测氯盐和硫酸盐侵蚀下混凝土的服役寿命，为海工混凝土服役期内的质量控制提供理论支撑。

3.1 氯盐侵蚀

氯离子侵蚀是导致钢筋锈蚀最主要的原因，20世纪70年代，Callepardi[52]首次提出采用Fick第二定律描述氯离子在混凝土中的扩散行为，该模型成为后续研究中氯离子扩散行为的主要模型，即

(16)

式(16)中：C为氯离子浓度，以氯离子质量占胶凝材料质量百分比表示；x为距混凝土表面距离；t为暴露时间；D为氯离子扩散系数。

然而，菲克第二定律在初始时假定混凝土材料为各项均质性，氯离子与混凝土中各部分不发生反应，无法完全适宜复杂材料在多变环境条件下的扩散规律。且氯离子扩散系数随混凝土龄期增长而衰减，公式中采用定值进行计算过于理想化，对混凝土的预估行为没有普适意义，主要应用于环境变化单一的室内试验计算。现如今，大多氯离子扩散行为仍旧基于此种模型进行改进，张菊辉等[53]、陈宣东等[54]通过数值模拟，验证了模型在特定条件下的可行性。杜梓鹏等[55]借助菲克第二定律和ANSYS软件中的自带模块完成了氯离子扩散的影响因素研究。随着越来越多学者对菲克第二定律的完善，余红发等[56]考虑氯离子时间依赖性对菲克第二定律模型进行修正，解决氯离子扩散过程中存在的非稳态齐次扩散问题，得到扩散方程为

(17)

式(17)中：D=Dit-m，Di为单位时间内的有效氯离子扩散系数，h为时间依赖性常数。

改进后的扩散方程虽然考虑参数的时变性，仍存在难点，即Di不是一个可测定值，它是随着时间和环境而逐步变化的。这就使得改进后的扩散方程应用范围大大降低，仅局限于已知扩散系数规律的地区，且没有普适性。朱彬荣[57]基于改进的氯离子扩散模型，提出基于修正菲克第二定律完全解的理论模型为

cf=c0+(cs+c0)×

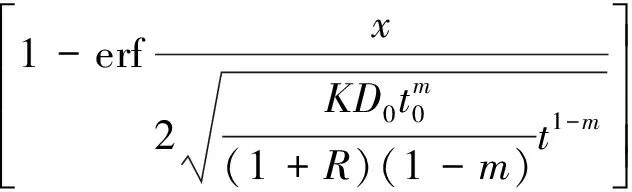
(18)

式(18)中：cf为自由氯离子浓度；c0为混凝土内初始氯离子浓度；cs为混凝土暴露表面的氯离子浓度；K为混凝土氯离子扩散性能的劣化效应系数；x为距混凝土表面的距离；D0为水化龄期为t0时的混凝土氯离子扩散系数；m为试验常数，取0.64；R为结构缺陷参数；erf为误差函数。

上述模型通过初始和外表面氯离子浓度有效解决扩散系数不可测定化的困难，可应用于任何区域，也不需要担心环境变化对扩散系数的影响。而Jiang等[58]采用双重循环迭代，以割线斜率代替切线斜率预测混凝土结构的可靠性和寿命，该迭代模型为

(19)

式(19)中：X为扩散模型的参数；t为服役时间；βt为t时刻的可靠度指标；tk为混凝土结构的服役寿命。

以往的计算模型基于隐函数计算，虽能确定变量与预测寿命之间的关系，但不一定可化为显函数进行直接计算，隐函数在推导过程中难以准确量化数据的可靠性，给数据的验证带来一定困难。迭代化计算将问题可视化，适用于绝大多数氯盐侵蚀环境下，内部不含有钢筋的混凝土寿命预估。

现有海洋环境下混凝土结构氯离子扩散模型除了基于菲克第二定律，还可采用Monte-Carlo方法[59]、Copula函数[57]和结构氯离子表面浓度变化[8]来预测海工混凝土的服役寿命，及时预测结构状态，在建筑物完全破坏前进行修缮，降低维修费用。虽然优化后的氯离子扩散模型及迭代模型可以较好模拟海工混凝土服役环境，但模型中并未考虑钢筋锈蚀的影响，这可能会高估其使用寿命，造成难以预测的损害。

3.2 硫酸盐侵蚀

硫酸盐腐蚀也是影响海工混凝土耐久性的重要因素之一。海水环境中的硫酸根离子与混凝土中的氢氧化钙反应生成难溶性硫酸钙，固相体积膨胀，造成混凝土开裂。当结构物裂缝数量较多、深度较大时，混凝土表层区域出现剥落现象。

杨永敢[60]基于混凝土表面剥落厚度衡量混凝土性能，采用菲克第二定律，建立硫酸根等效侵蚀与侵蚀时间关系模型为

(20)

式(20)中：XD为等效侵蚀深度；CE为单位混凝土能够消耗的最大硫酸根离子含量；C0外界硫酸根离子浓度；CL为初始时混凝土中含有的硫酸根离子含量；t为侵蚀时间；D为混凝土中硫酸根离子扩散系数。

海工混凝土所处环境十分恶劣，海洋中包括硫酸盐、氯盐、镁盐、微生物及各类对混凝土结构造成损害的物质，上述模型仅考虑硫酸盐侵蚀来预测结构物寿命存在一定局限性，可能是非保守的，可应用于针对硫酸盐侵蚀为主要研究对象的混凝土结构的寿命预估。李刊等[61]利用电化学，基于Weibull 分布对混凝土进行无损寿命预测，以腐蚀电流密度作为指标，预测硫酸盐、镁盐和氯盐耦合环境下混凝土的服役寿命，得到寿命失效分布函数F(t)、概率密度函数f(t)和失效率函数λ(t)分别为

(21)

(22)

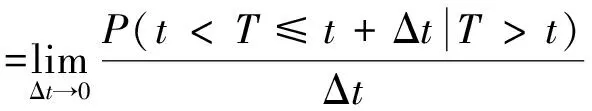
(23)

式中：U、V、δ分别为混凝土结构物的形状、尺度、位置参数；T为寿命产品失效首次达到失效阈值的时间；t为时刻。

通过引入Weibull 分布，针对现有定量评价海工混凝土耐久性仅在氯盐或硫酸盐单一环境下的局限性，更好模拟实际海水环境。徐存东等[62]通过回弹法和超声检测法对Weibull 分布预测模型进行验证，结果良好。说明Weibull 分布对多盐类耦合复杂环境下的海工混凝土寿命预测存在积极意义，也为后续增加耦合因素研究提供指导方向。

4 结论与展望

混凝土寿命预测模型影响因素较多，如碳化深度、碳化速率、环境参数、侵蚀时间等，基于耐久性能的混凝土寿命预测的关键是选择合适的模型和参数，通过模拟实际环境下混凝土的服役状况，采用加速试验、数学模型预测或概率分析对其寿命进行预测。通过归纳和总结现有混凝土寿命预测模型可以得出如下结论。

(1)混凝土碳化、酸雨腐蚀和疲劳破坏是结构混凝土存在的主要耐久性问题，分别基于碳化寿命准则、多变量灰色模型及Paris裂纹扩展定律对结构混凝土进行寿命预测，通过定量分析准确预测混凝剩余寿命，为结构性能安全提供保证。

(2)裂缝是道路混凝土破坏的主要原因，基于现有疲劳混凝土破坏机理，分别采用S-N曲线，Paris公式和基于能量耗散的方法预测道路混凝土疲劳寿命，通过可靠度分析和计算可保证混凝土在服役期内的安全性。

(3)氯盐和硫酸盐腐蚀是影响海工混凝土耐久性最显著的因素，采用菲克第二定律作为描述氯离子在混凝土中扩散行为的基本模型，以菲克第二定律完全解和双重迭代预测氯盐腐蚀下混凝土的服役寿命。基于Weibull 分布定量评价复杂环境下混凝土性能劣化情况，为海工混凝土服役期内的质量控制提供依据。

现有基于耐久性混凝土寿命预测模型种类较多，相关参数较为完善，但混凝土服役环境多变，且近年来极端天气增加，需加强现场环境监测，积累不同服役环境下的混凝土寿命预测相关参数，以期提高后续混凝土预测的准确性和可靠性；再者现有中外规范均只考虑混凝土在单一环境中的耐久性，预测方法与模型也未能提及多因素耦合作用下混凝土的服役寿命，应加强相关方面的研究；最后，现有预测模型基本基于新建混凝土相关数据进行预测，而在实际情况下，中国大部分构筑物都经过小修、中修，甚至是大修，维修过后的混凝土结构是否还能依照最初的预测模型预测其服役寿命还有待商榷，需要相关数据来进一步验证。若不满足，则需基于已修复混凝土提出新的寿命预测模型。