基于Bessel和Meijer-G函数的楔形和锥形悬臂梁振动分析
周坤涛, 杨 涛, 葛 根, 郝淑英, 张琪昌
(1.天津工业大学 机械工程学院,天津 300387; 2.天津理工大学 工程训练中心,天津 300384;3.天津理工大学 机械工程学院,天津 300384; 4.天津大学 机械工程学院,天津 300072)
变截面梁具有优化质量和强度分布等特点,近年来被广泛的应用在航空、机械、建筑、桥梁及能量采集器等领域,随着科学技术的快速发展,变截面梁的设计与加工更趋成熟,为变截面梁的广泛应用提供了可能。与等截面梁相比,变截面梁的控制方程为四阶变系数偏微分方程,通常情况下很难得到解析解[1-2]。
国内外学者对变截面梁进行了大量研究,Silva等[3]将变截面梁假定为厚度不变,宽度线性变化的截面梁,采用四个Meijer-G函数的线性组合表示振型函数,得到了梁的基频和振型,发现线性问题近似解中可忽略不计的误差也会对非线性问题的分析结果产生重要影响,进一步强化了线性基频和振型精确解的重要性。国内学者崔灿等[4]基于欧拉-伯努利梁理论,采用分段传递矩阵法对变截面梁的振动进行了研究,该方法的精度依赖于分段数的选取;周坤涛等[5-6]利用超几何函数和Meijer-G函数的线性组合表示振型函数,对变截面进行自由振动与非线性振动研究,通过数值模拟与试验方法验证了其理论。然而,以上研究选取的变截面梁面积和惯性矩均为线性变化。针对宽度不变厚度线性变化的楔形梁以及宽度和厚度均线性变化的锥形梁国内外学者也进行了大量研究,取得了丰硕成果。众所周知,当宽度不变厚度线性变化时,其面积呈线性变化而惯性矩会呈3次方系数变化;当宽度与厚度均发生线性变化时,其面积会呈2次方系数变化而惯性矩则会呈4次方系数变化,这给解析解的求解带来很大的困难。针对这一求解难点,Mabie等[7-10]均基于贝塞尔函数理论对楔形或锥形梁进行了研究,虽然其设解的形式不同,最终都得到了具有经典边界条件的楔形和锥形变截面梁的精确频率方程及基频,但是该方法严重依赖于方程的形式,方程必须为规范的Bessel方程;Rao[11]采用伽辽金方法得到了变截面梁的基频;Conway等[12]利用近似多项式表示贝塞尔函数计算锥形梁和楔形梁在简支、固支和自由边界条件下的近似基频;Naguleswaran[13]采用Frobenius级数方法给出了欧拉-伯努利楔形梁和锥形梁的直接解,并以列表的形式给出了精确的基频;Gaines等[14]考虑剪切变形和转动效应,利用瑞利-里兹法对锥形和楔形变截面梁前三阶固有频率进行了计算;Lee等[15]利用格林函数进行拉普拉斯变换分析了变截面梁的振动。Ho等[16]采用微分变换法研究了弹性约束边界条件下变截面梁的振动。Hsu等[17]采用AMDM(Adomain modified decomposition method)法对楔形和锥形变截面梁进行振动分析,得到的线性基频和振型具有很高的精度,但该方法在四阶积分时由于非线性几何函数会产生奇异性,一般需要进行级数展开,同时求解时需要进行大量的迭代计算,比较耗费机时,其结果的收敛性在很大程度上取决于级数截断项数的选取。近年来,Lee等[18]对楔形和锥形欧拉-伯努利梁的偏微分方程采用Frobenius幂级数进行设解,提出一种求解楔形和锥形变截面梁的自由振动特性的传递矩阵法。Keshmiri等[19]采用改进的数学方法,利用ADM(Adomain decomposition method)法推导了非线性锥形截面欧拉-伯努利梁的特征方程和模态函数,给出了具有不同锥比的指数函数锥形梁和三角函数锥形梁的固有频率和振型,但该方法在求解过程中依然存在高阶泰勒展开,导致计算迭代过程会不断叠乘,计算仍然耗费机时。李伟等[20]采用微分变换法(differential transform method)推导了圆形变截面梁横向振动偏微分方程的级数解,并利用有限元软件ABAQUS验证了所提方法的精确性。
针对楔形和锥形变截面梁已有的研究成果,本文提出一种无需迭代及近似截断的Bessel函数与Meijer-G函数线性组合的振型函数,该方法不依赖于楔形和锥形变截面梁的弯曲振动的运动方程是否为标准的Bessel形式,可直接利用Mathematica等计算软件进行求解,通过给定相应的边界条件即可快速求解欧拉-伯努利楔形和锥形梁的线性基频和振型;随后将本文的振型代入非线性振动控制方程中,考虑梁几何非线性和惯性非线性的影响,利用多尺度法,研究楔形和锥形梁在主共振下的非线性幅频响应,Hsu等研究中的计算结果验证了本文提出的求解振型函数方法的精确性和可靠性。
1 物理建模
如图1所示的欧拉-伯努利梁为厚度和宽度沿长度方向均逐渐变窄的悬臂梁,弹性模量为E,密度为ρ,长度为L,固定端宽度为b0,厚度为h0,自由端宽度为bl,厚度为hl。建立图1(a)所示直角坐标系,x轴位于梁的中性轴,y轴沿梁厚度方向,z轴沿梁宽度方向,s轴为沿梁长度方向固定在中性轴上的弧坐标。
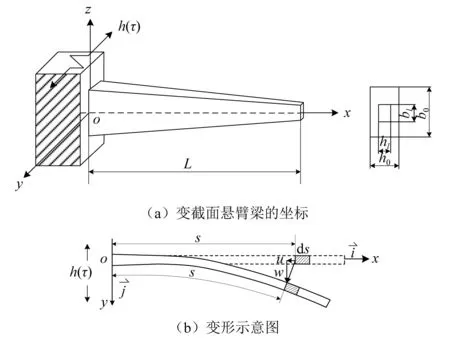
图1 欧拉-伯努利梁理论Fig.1 The Euler-Bernoulli beam theory
定义梁宽度和厚度方向上的截面变化系数分别为:βb=1-bl/b0,βh=1-hl/h0,则截面宽度b(s)和厚度h(s)可以表示为
(1)
由式(1)可以得到坐标s处梁的横截面积A(s)和截面惯性矩I(s)
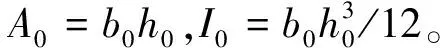
假定梁固定端受横向简谐位移激励h(τ)作用产生非线性弯曲振动,忽略梁的重力效应和转动效应。图1(b)为坐标s处微段ds的变形图,该微元段变形包含沿x轴水平位移u(s,τ)和沿y轴的横向位移w(s,τ),图中微元段的位移可表示为
d(s,τ)=u(s,τ)i+[w(s,τ)+h(τ)]j
(3)
其中微元段轴向位移为
(4)
式(4),ξ为虚拟符号。对式(3)求一阶导数,并考虑式(4),即可得到微元段的速度vP。
(5)
式中,(·)为对时间τ求偏导。
当悬臂梁在外激作用下振动时,其动能T为
(6)
悬臂梁振动时的弯矩为
(7)
式中,(′)为对s求偏导。
梁的弯曲势能为
(8)
将式(7)代入式(8)中,略去高阶小量,可得
(9)
系统的耗散函数D可表示为
(10)
假定第i阶梁的位移表示为
wi(s,τ)=φi(s)qi(τ)
(11)
利用Lagrange方程
(12)
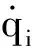
(13)
(14)
2 振型函数和线性基频
为确定微分方程式(14)中的系数项,需要求得满足正交条件和边界条件的模态函数φi(ς)。为了得到梁的频率和模态函数,首先要求解梁的线性特征值问题。由Euler-Bernoulli理论,该非均匀弹性梁横向自由振动的偏微分方程
(15)
考虑悬臂梁的边界条件,固定端约束处时挠度与转角分别为零,即s=0可得
(16)
在自由端弯矩与剪力分别为零,即s=L可得
(17)
采用相同的无量纲,将式(11)代入式(15)中,可得
[(1-βbς)(1-βhς)3φ″(ς)]″η=0
(18)
假定η(t)=c1cos(β2t)+c2sin(β2t), 其中β2为梁的固有圆频率,c1,c2为未知的参数,则式(18)可变为
(19)
无量纲边界条件可以重新表示为
φ(0)=0,φ′(0)=0
(20)
(21)
2.1 Euler-Bernoulli楔形梁(βb=0,βh=α)
考虑梁宽度不变,厚度沿x方向线性渐细变化的楔形梁,则式(19)可简化为
(22)
为求解式(22)的解,将振型函数φ(ς)直接表示成第一类Bessel函数与Meijer-G函数线性组合的形式
φi(ς)=C1iφ1i+C2iφ2i+C3iφ3i+C4iφ4i
(23)
式中:Ci为待定系数;i为模态的阶次,则
(24)

为确定式(23)中的待定系数Ci和βi,需考虑式(20)和式(21)可得
(25)
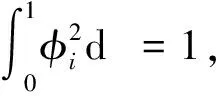
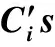
表1 楔形梁前三阶模态的系数βi和Tab.1 The βiand coefficients of the first three modes for wedge beam
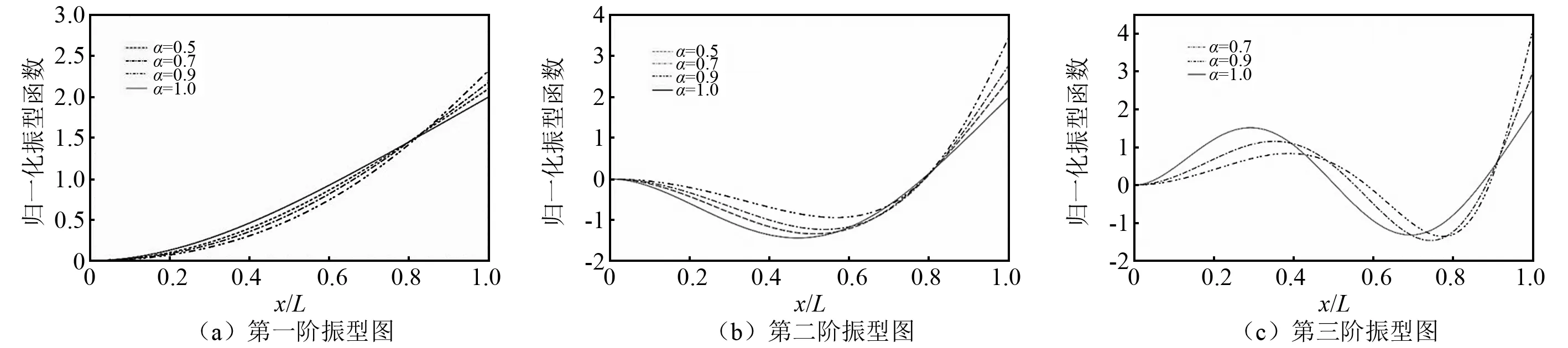
图2 楔形梁前三阶振型Fig.2 First three modal shape for wedge beam
为验证本文方法的正确性,将计算所得的结果与文献结果进行比对,通过比对表2数值可以看出,本文计算结果与已有文献结果高度吻合,充分说明本文方法具有很好的计算精度。

表2 楔形悬臂梁前三阶无量纲固有圆频率Tab.2 Non-dimensional first three natural frequencies for a linearly tapered cone cantilever beam
为进一步说明本文所提方法在计算时间和收敛性方面的优势,选取Windows10操作系统,其中CPU为i5-7300HQ,内存为8 G的笔记本电脑,采用Mathematica11.2软件编制计算程序,以截面系数α=0.5的楔形梁为例,比对了本文方法和Hsu等方法的计算时间,如表3所示。
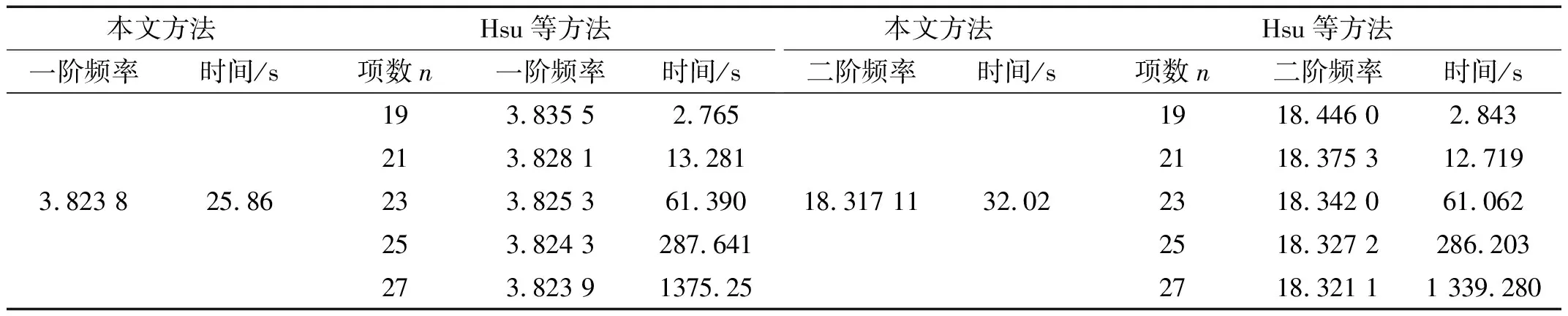
表3 截面系数α=0.5的楔形梁前两阶无量纲固有频率计算时间Tab.3 Calculation time for first two natural frequencies of tapered wedge beams with ratio α=0.5
从表7中可以看出,本文方法能直接得到精确的计算结果,无需考虑展开项数,而AMDM法的计算精度则严重依赖于级数项数n的选取,由Hsu等的研究可知,一般n至少超过27时才能得到较精确的结果。从表7中可以发现,求解一阶固有频率时,本文方法只需25.86 s,Hsu等的研究则需要1 375.25 s,二阶固有频率本文方法计算时间为32.02 s,而文献[17]则需要1 339.28 s。通过比较两种方法的计算时间,证明本文方法具有计算时间短,收敛快等特点。本文方法在求解截面系数α≤0.5的梁第三阶固有频率时会出现计算误差或者求解不成功的现象,因此没有给出第三阶固有频率的具体结果。但对于α>0.5的楔形梁前三阶固有频率的求解,该方法具有求解快,精度高,适用性好等优势。
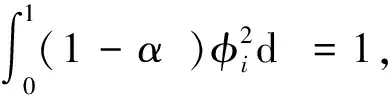
γiχicos(Ωt)
(26)
式中:μi为无量纲的阻尼系数;ωi为无量纲的固有频率;α1i为无量纲弯曲非线性项系数;α2i为无量纲惯性非线性项系数;γi为无量纲外部激励系数,具体系数为
(27)

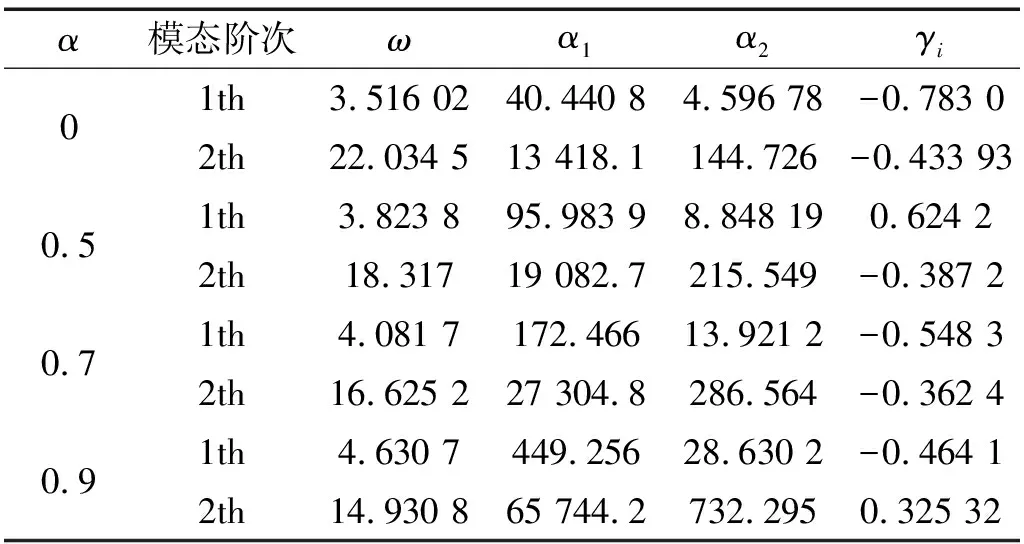
表4 楔形梁前两阶模态的方程系数Tab.4 The coefficients of first two modes for wedge beam
2.2 Euler-Bernoulli锥形梁(βb=βh=α)
考虑梁宽度和厚度沿x方向按相同的截面系数线性渐细变化的楔形梁,则式(19)可简化为
(28)
采用与上文相同的方法,将振型函数φ(ς)表示成第二类Bessel函数与Meijer-G函数线性组合的形式,即
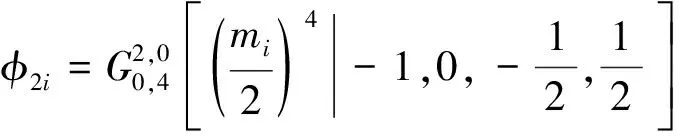
(29)
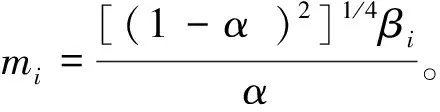
考虑式(20)和式(21),其边界条件可表示为
φ(0)=0,φ′(0)=0
(30)
(31)
将式(29)代入式(23)后,考虑式(30)和式(31),按照2.1节中的方法即可得到振型函数系数Ci和βi,如表5所示。
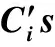
表5 锥形梁前三阶模态的系数βi和Tab.5 The βi and coefficients of the first three modes for cone beam
为验证本文理论的计算精度,选取不同截面系数的锥形悬臂梁计算了前三阶无量纲固有圆频率,如表6所示,从表中可以看出,一阶固有频率随着截面系数的增加逐渐变大,而二阶和三阶逐渐变小。
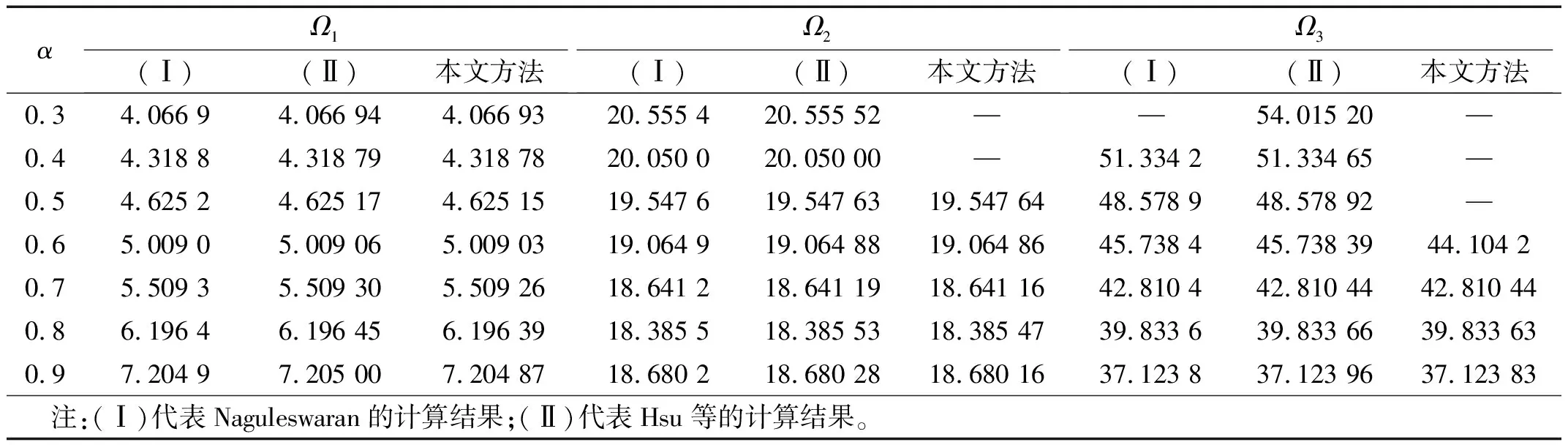
表6 锥形变截面悬臂梁前三阶无量纲固有圆频率Tab.6 Non-dimensional first three natural frequencies for a linearly tapered cone cantilever beam
同理,为说明本文方法在求解时计算时间和收敛性方面的优势,选取α=0.7的锥形变截面梁为例,比对了该方法和Hsu等的方法前二阶固有频率的计算时间,如表7所示。

表7 截面系数α=0.7的锥形梁前两阶固有频率计算时间Tab.7 Calculation time for first two natural frequencies of tapered cone beams with ratio α=0.7
从表7中可以看出,与楔形截面梁计算规律一致,本文方法在处理锥形截面梁固有频率时同样具有计算时间短,收敛快等特点,而AMDM法计算精度收敛性则依然严重依赖级数项数的选取,但时间会成倍增加。
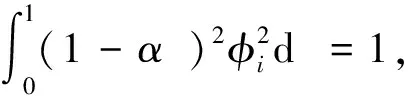
(32)
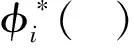
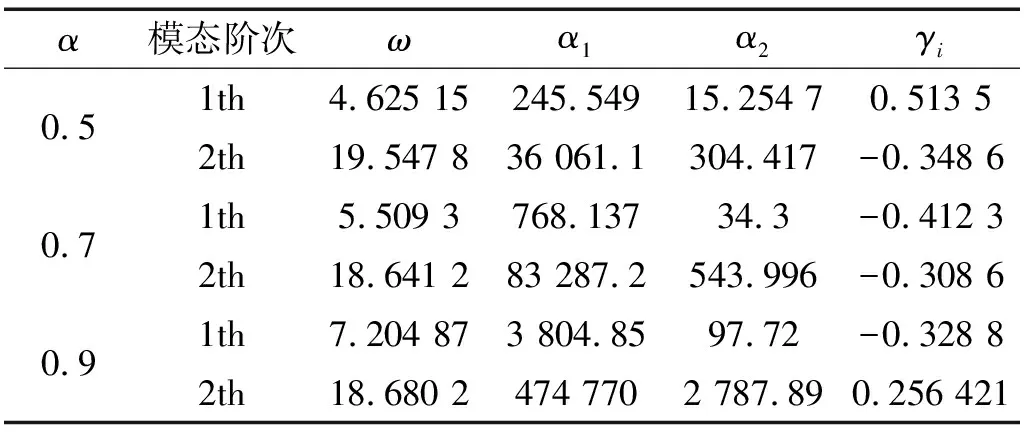
表8 锥形梁前两阶模态的方程系数Tab.8 The coefficients of first two modes for wedge beam
3 主共振响应
3.1 多尺度法
为探讨变截面梁在主共振下的动态响应,假定外激频率接近模态频率(Ω≈ω)且不考虑内共振的情况,采用多尺度法计算变截面悬臂梁的幅频响应。
在主共振情况下,假定
cos(Ωit)=cos[(ωi+σ)t]
(33)
式中,σ为调谐参数。将式(33)代入式(26)中可得
γiχicos[(ωi+σ)t]
(34)
将时间变量展开成多个不同尺度的时间变量
Tn=εnt,n=0,1,2,…
(35)
引入如下微分算子
(36)
将模态坐标ηn(t)展开成如下形式
ηn(t;ε)=η0(T0,T1)+εη1(T0,T1)+ο(ε2)
(37)
将式(37)代入式(34),并考虑非线性项,阻尼项,力项均为同阶小量,令ε0,ε1的系数为零可得
(38)

(39)
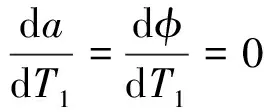
(40)
3.2 幅频响应
以βb=0,βh=α=0.5楔形梁为例,假设无量纲外激加速度χ=0.019 4,阻尼比μ=0.05,将表3中参数代入式(40),可得前二阶主共振幅频响应曲线,从图3中可以看出,一阶幅频响应曲线向右偏,呈现硬特性;二阶幅频响应曲线向左偏,呈现软特性。

图3 βh=α=0.5楔形梁在外激作用下的幅频响应曲线Fig.3 Amplitude-frequency response curve of wedge beam under external excitation for βh=α=0.5
为验证本文幅频响应曲线的正确性,选取Hsu等所用的AMDM法得到的振型函数,将其代入式(27),得到相应的系数,随后代入式(40)同样可以得到幅频响应曲线,从图中可以看出,两种方法所得到的幅频响应曲线高度吻合。众所周知,线性基频和振型函数微小的误差,将会对非线性分析产生很大的影响,这也充分说明本文方法得到的振型函数与AMDM法得到的振型函数高度吻合。
同理,以βb=βh=α=0.7的锥形梁为例,采用同样的外激加速度作用,得到了前两阶主共振幅频响应曲线,从图4中可以看出,一阶幅频响应曲线两种方法吻合很好,二阶幅频响应曲线两种方法仅有微小的误差,其原因可能是AMDM法振型函数的精确性与级数展开及截断项数的选取有关,而本文理论方法则不需要考虑近似截断项数。

图4 βb=βh=α=0.7锥形梁在外激作用下的幅频响应曲线Fig.4 Amplitude-frequency response curve of cone beam under external excitation for βb=βh=α=0.7
4 结 论
(1)本文提出了一种快速求解楔形和锥形截面悬臂梁线性基频和模态函数的新方法,该方法不依赖于楔形和锥形截面梁的弯曲振动的运动方程是否为标准的Bessel形式,直接利用Bessel函数和Meijer-G函数线性组合构建新的振型函数,求解过程无需大量迭代运算和级数近似截断。通过理论计算得到的线性基频与已有文献结果高度吻合,验证了本文方法的正确性。
(2)线性基频和振型函数微小的误差,将会对非线性幅频响应分析产生很大的影响。从本文得到的幅频响应曲线图可以看出:采用Bessel函数和Meijer-G函数线性组合构建新的振型函数与AMDM法得到的振型函数一样,具有很高的精度,验证了本文振型函数的正确性。
(3)本文方法在处理变截面参数较大的楔形和锥形梁时有更好的适用性,该方法可为楔形和锥形截面梁固有频率及振型函数的求解提供了新的思路。

