平面钢框架在撞击荷载作用下的抗连续倒塌分析
乔惠云, 郭壮壮, 陈 誉, 张明锋, 丘华生, 王 征
(1.福建工程学院 土木工程学院,福州 350118;2.福州大学 土木工程学院,福州 350116;3.中煤建设集团有限公司,南昌 330001;4.中国建筑第四工程局有限公司,广州 510665;5.福建省协兴建设有限公司,福州 350199)
多种自然灾害和人为因素都可能造成结构连续倒塌,比如地震[1]、爆炸[2]、撞击[3]等极端荷载都可能引起结构局部破坏,甚至导致结构整体连续倒塌。抗连续倒塌研究经常抛开引起倒塌破坏的原因,直接拆除关键柱[4],研究剩余结构的抗倒塌性能。Yang等[5-7]通过直接拆除中柱后的子结构拟静力试验,研究不同节点形式下的悬链线效应。课题组[8-9]也采用直接拆柱法研究节点削弱后子结构的其抗倒塌机制。李国强等[10-12]采用直接去柱法对平面框架进行抗连续倒塌试验研究。Lu等[13]、Qian等[14]分别对带楼板的框架结构进行拆柱后的试验研究。关于直接拆柱法的理论研究,钱稼茹等[15]采用集中塑性铰杆模型研究拆柱后的动力效应。Xu等[16]基于能量平衡理论采用Pushdown方法分析拆柱过程。Alashker等[17]提出一种增量模型跟踪楼板系统在拆柱后的损伤演化。
需要注意的是,具体灾害可能引起特殊的受力方式和破坏模式,比如师燕超等[18]研究爆炸灾害对梁柱构件及其节点的冲击力破坏。靠近繁忙道路的临街建筑非常容易受到车辆等的撞击,大多数研究主要考虑柱的抗冲击性能或抗冲击加固措施。朱翔等[19-20]对外包钢管复合柱进行抗冲击试验。Wang等[21]、史艳丽等[22]分别对钢管混凝土组合构件进行横向撞击荷载下的试验研究。Huo等[23]进行了一系列落锤冲击钢框架梁或节点的试验。鲜有研究考虑柱被冲断后剩余结构的抗倒塌性能,本文分析撞击荷载引起的多层框架中柱失效后的抗倒塌性能,并与传统直接拆柱法对比,随后分析框架结构在不同质量、速度等撞击荷载作用下的动力响应。
1 平面钢框架直接拆柱法分析
本章首先模拟已有多层框架直接去中柱试验,李国强等对2层4跨平面钢框架采用直接拆柱法,研究多层框架中柱瞬时失效后框架的动力反应特性,用来与撞击拆柱法模拟结果对比。
1.1 模型参数
试件荷载布置如图1所示,第1、第2层的层高分别为H1=1 227 mm,H2=1 054 mm,跨度为L=2 054 mm。框架梁和柱均采用高频焊接H型钢,截面尺寸为H54×50×4×4 mm,梁柱节点都采用全焊节点。失效跨和相邻跨的配重大小分别为P1= 3.85 kN和P2= 2.1 kN。试件和配重安装就位后,瞬时拆除中柱引发结构连续倒塌。

图1 试件的立面图与荷载布置Fig.1 Elevation and load distribution diagram
1.2 直接拆柱法模拟
被拆除中柱采用ABAQUS软件中的梁单元B32建立,而剩余框架结构采用壳单元S4R建立,梁单元和壳单元采用*kinematic coupling命令进行的耦合,将壳单元截面上所有的点都耦合到梁单元的端部,如图2所示。节点区网格加密,网格尺寸为12.5 mm,节点区外的单元尺寸为25 mm。约束柱脚沿X,Y,Z方向的平动和转动,以模拟刚性柱脚。为使有限元模型固有频率与试验的真实频率一致,配重没有作为外荷载施加到框架梁上,而是折算成一定体积和密度的质量块悬挂在配重位置上[24]。配重作为外荷载时结构第一阶频率ω′n=13.06 Hz,配重作为质量块的第一阶频率ωn=8.48 Hz。采用在INP文件中加入语句*MODEL CHANGE, TYPE = ELEMENT, REMOVE模拟中柱拆除,拆柱时间取为0.01 s,小于剩余结构第1阶竖向自振周期(T1= 0.74 s)的1/10[25]。
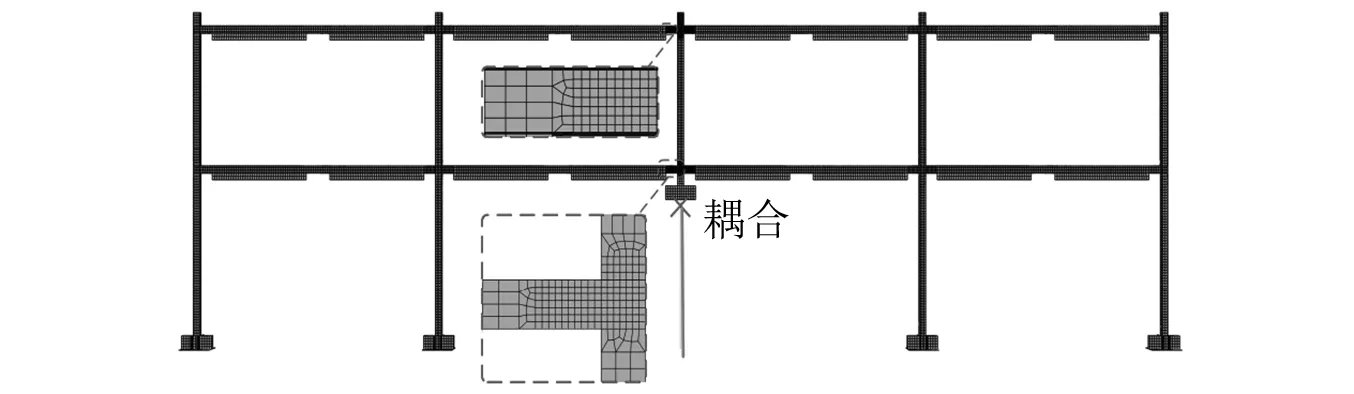
图2 试件的有限元模型Fig.2 Finite element model of specimen
中柱突然失效,材料受应变率影响很大,钢材的应变率采用Cowper-Symonds模型[26],屈服应力与应变率的关系为
(1)

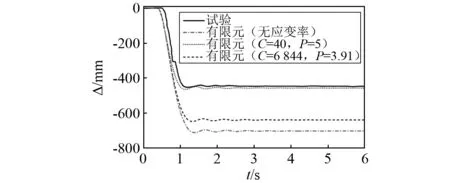
图3 失效中柱正上方节点的位移时程Fig.3 Displacement directly above the failed column
图4为有限元和试验破坏结果对比,整体变形和节点转角均一致,有限元模型反应梁端翼缘的屈服情况,可以模拟多层框架结构在中柱失效后的动力性能。撞击拆柱法模拟也在此平面框架基础上完成。

图4 有限元和试验破坏结果对比Fig.4 Comparison of failure results between FEM and test
2 平面钢框架撞击拆柱法分析
2.1 撞击模拟验证
Huo等采用落锤冲击法研究撞击荷载作用下钢梁力学性能。钢梁截面尺寸为H250 mm× 125 mm× 6 mm× 9 mm,有效跨度L=2 500 mm。落锤的质量m1=450 kg,落锤高度H=3.2 m,撞击速度v=7.9 m/s。采用ABAQUS的8节点减缩积分单元(C3D8R)建立精细化有限元模型。用直径200 mm和高度均为200 mm的圆柱体模拟落锤,落锤的速度由预定义场施加。落锤与钢梁的接触面采用通用接触,接触面法向为“硬”接触,切向摩擦因数为0.3。
撞击力F时程曲线如图5所示,曲线包含三个阶段:峰值段、平台段和下降段,将模拟结果与试验结果对比,两者吻合较好。钢梁撞击点的位移δ时程曲线如图6所示,模拟值与试验值相比误差较小,认为本节采用的模型可以模拟动力撞击问题。
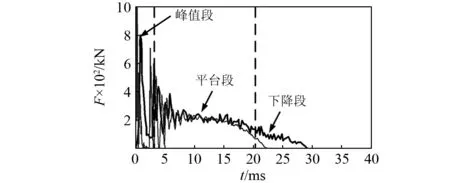
图5 撞击力时程曲线Fig.5 Impact force-time history curves
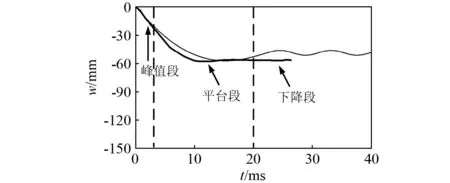
图6 撞击点位移时程曲线Fig.6 Displacement-time history curves of impact point
由撞击力和位移时程曲线还发现撞击力处于峰值段时,钢梁撞击点的位移较小,还来不及变形,钢梁最大位移发生在撞击力的平台段。图7的应力云图也能说明该现象,峰值段的应力最大值出现在撞击点附近;达到平台段后,整根钢梁参与抵抗撞击力;下降段撞击力逐渐减少,甚至落锤回弹,钢梁随后按自身固有频率震荡。
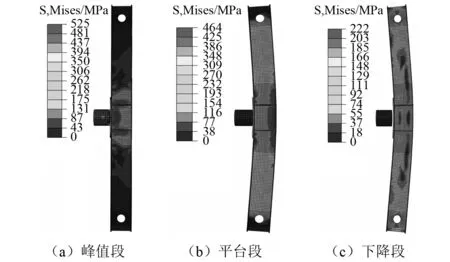
图7 撞击各阶段应力云图Fig.7 Stress nephogram of impact stages
2.2 撞击力简化模型
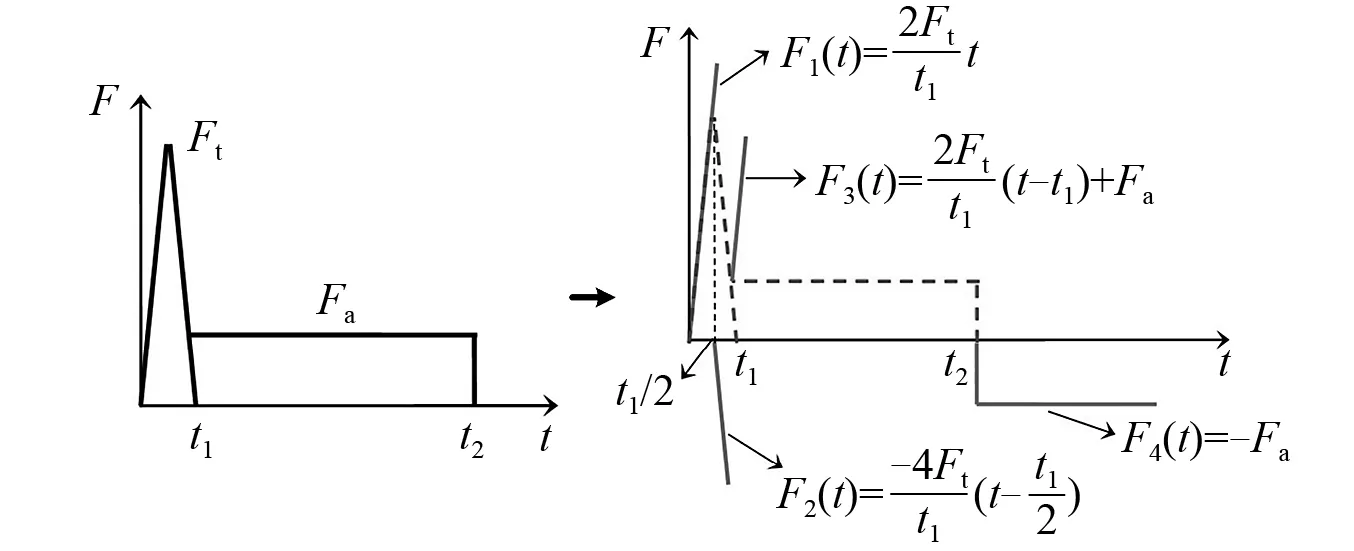
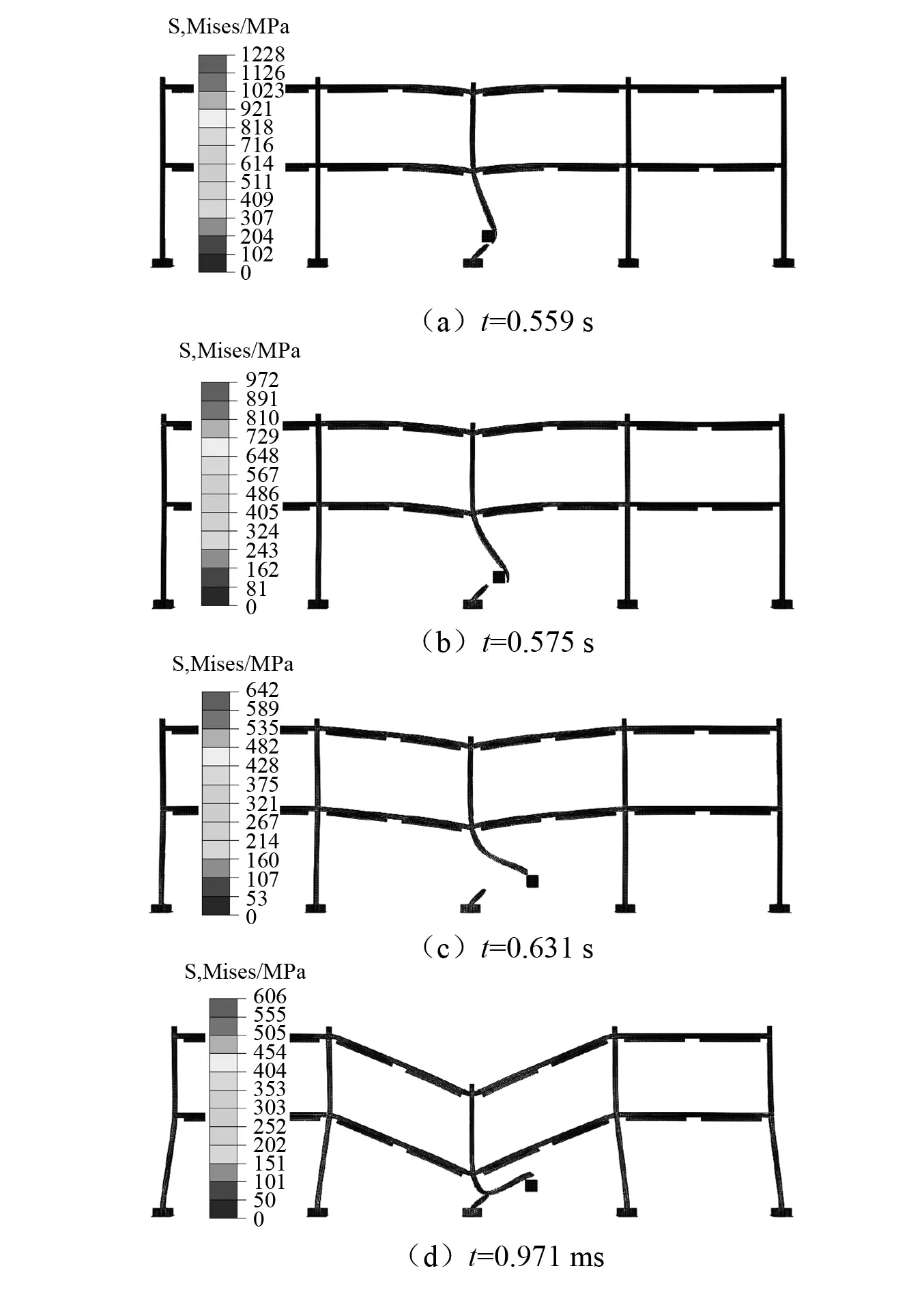
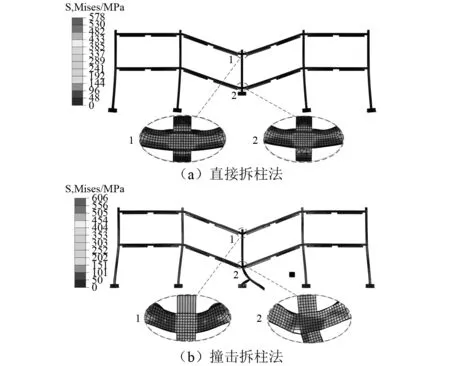
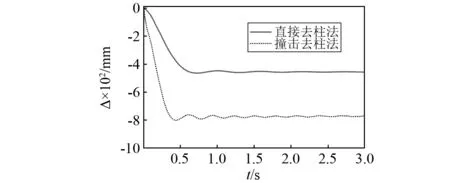
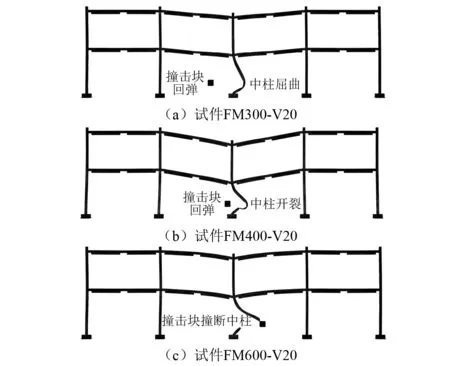
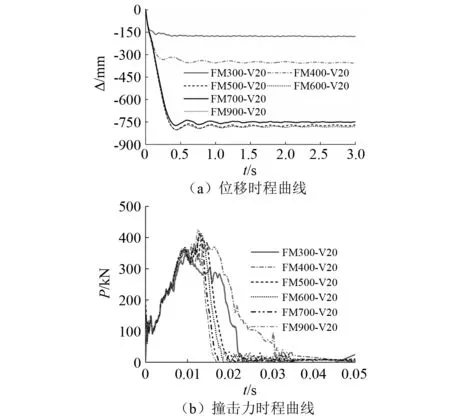
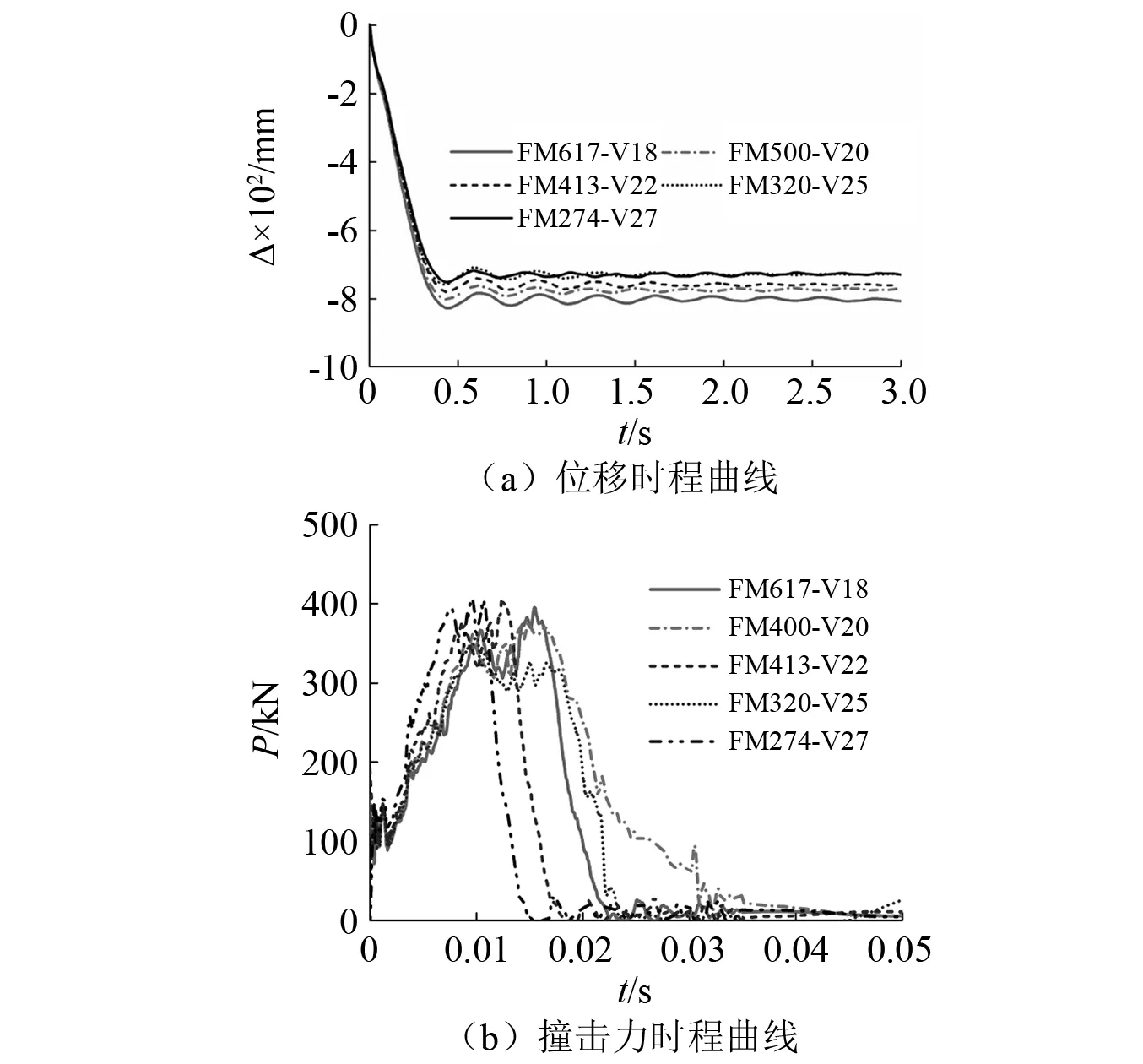
将撞击力时程曲线的三个阶段简化为几个简单的脉冲组合,比如,把峰值段(0≤t≤t1)简化为三角形脉冲,把平台段和下降段(t1 图8 撞击力时程曲线简化Fig.8 Simplification of impact force-time history curve 撞击力F(t)是随时间t变化的函数,对应的撞击力冲量函数为I(t),在任意时刻,冲量函数I(t)可以表示撞击力F(t)对时间t的积分 (2) 式中,Itri为峰值段三角形脉冲的冲量,若撞击力的峰值为Ft,Itri可表示为 (3) 同时,平台段和下降段的冲量之和Irec可以表示为 (4) 平台段和下降段简化的矩形脉冲持续时间为t2-t1,撞击力平台值Fa可由Irec表示为 (5) 结构体系在撞击力作用下的动力响应可以简化为几个脉冲激励反应的叠加,比如撞击力对应的时程曲线可以简化为图9所示四个激励函数F1(t),F2(t),F3(t)和F4(t)的叠加。简化模型的关键参数有:撞击力峰值Ft、撞击力平台值Fa、峰值段结束时间t1和下降段结束时间t2。 图9 撞击力简化为简单脉冲反应Fig.9 Simple pulse simplified by impact load 撞击过程持时较短,其中有效撞击不超过0.1s[29],阻尼力来不及在这么短的作用时间内发挥作用,所以撞击力作用下的运动微分方程不考虑阻尼部分,可以表示为 (6) (7) 激励函数Fi(t)可分解为持续时间为无穷小的脉冲序列,采用Duhamel积分[30]。得到对应的位移反应函数ui(t),表示为 (8) (9) (10) (11) (4)激励函数F4(t)。将F4(t)=-Fa代入式(8)计算得到 (12) 改变撞击质量和撞击速度,使中柱被撞断,研究极端情况下剩余结构的抗倒塌性能。撞击拆柱模型选用第1节平面钢框架,拆柱方式由直接拆柱法改变为撞击拆柱法。撞击中柱的块体采用方形刚体代替,撞击块所具有的质量和速度决定撞击能量。若撞击块的动能太小,使中柱只受轻微损伤,或者撞击块的动能太大,中柱被撞断后,撞击块仍以一定的速度继续运动并撞击相邻柱,使框架结构发生过度破坏,将不能与直接拆柱法的结果对比,所以在中柱的右侧设置方形防撞桶(如图10所示),桶的边长为0.1 m,长度为0.5 m,厚度为1 mm,用于消耗撞击块撞断中柱后的剩余能量,保护相邻柱不受撞击损坏。 图10 撞击拆柱法模型Fig.10 Model of impact column removal method (13) 关于钢材的应变率,Scholl等[32]和Somarathna等[33]分别对比了常用应变率模型的使用范围,Cowper-Symonds模型使构件在高速冲击以及高应变情况下的计算结果偏大,模型优点是计算参数较少。结构受车辆等撞击大多数为低速冲击,所以应变率仍选用Cowper-Symonds模型。 首先选用质量为500 kg的块体撞击中柱,其与中柱接触时速度为20 m/s,图11对比了受撞击框架模型在不同时刻的应力。在中柱被撞断时刻(见图11(a)),应力最大值发生在撞击点位置,其他位置应力较小,整个框架结构来不及变形,柱失效点正上方的位移为72 mm;在刚体与中柱间的撞击力衰减到0时刻(见图11(b)),原来由中柱承担的荷载转移到相邻其他结构,柱失效点处的位移为116 mm;在撞击结束时刻(见图11(c)),撞击刚体仍以速度5.6 m/s撞向防撞桶直至减速到0,剩余结构在竖向不平衡力作用下继续变形,柱失效点处节点的位移为550 mm;在结构出现较大的竖向变形时刻(图11(d)),被撞断的中柱上半段和下半段重新接触,此时柱失效点正上方节点的位移为782 mm,已经接近剩余框架结构稳定时刻的位移。 图11 受撞击框架在不同阶段的应力Fig.11 Stress of impacted frame at different stages 图12和图13对比了平面钢框架结构分别采用直接拆柱法和撞击拆柱法去除中柱的部分结果。图12为框架结构的节点破坏形式。采用直接拆柱法后(见图12(a)),框架梁柱节点的应力较小,且第一、第二层节点的应力变化接近,失效中柱的剩余部分还处于弹性状态,最大应力发生在各层梁的上下翼缘。采用撞击拆柱法后(见图12(b)),第一层梁柱节点在靠近撞击侧的应力较大,梁变形过大导致受撞击侧的梁下翼缘受拉开裂,另一侧梁翼缘和腹板受挤压屈服,而第二层梁柱节点还没有进入塑性状态。 图13为失效点正上方的竖向位移,撞击拆柱法达到稳定后的位移为759 mm,直接拆柱法达到稳定后的位移为447 mm,前者明显大于后者。结合图12应力分析,撞击力引起撞击点及中柱上下节点应力集中,在应力集中区域发生局部损伤破坏,且撞击力的峰值远大于中柱失效后的竖向不平衡力,进一步加剧构件初始损伤,带损伤的剩余结构在中柱失效后抵抗竖向不平衡荷载,使结构达到稳定后的变形较大。传统直接拆柱法没有考虑撞击力对节点和相邻区域的破坏,低估剩余结构的动力响应。为真实反应构件和节点对灾害的响应,框架抗倒塌研究最好结合具体灾害分析。 图12 节点破坏形式对比Fig.12 Comparison of failure modes of nodes 图13 位移曲线对比Fig.13 Comparison of displacement curves 为进一步分析框架受撞击荷载后的响应,改变撞击块的质量和速度,质量m从300~900 kg变化,速度v从15~30 m/s变化,试件基本参数如表1所示。 表1 试件的基本参数 试件名称与撞击块的质量和速度相关,比如试件FM300-V20中:F代表框架;M300表示撞击块质量为300 kg;V20表示撞击块速度为20 m/s。所有试件分为3组:试件从编号1~5分析撞击块速度变化对框架的影响;编号6~10分析撞击块质量变化对框架的影响;编号11~14分析撞击能量对框架性能的影响。 第1组模型中撞击块的质量为500 kg,速度从15 m/s逐渐增大到35 m/s,框架结构在中柱附近的破坏模式根据速度不同可以分为三种情况:第一种情况被撞中柱屈曲变形,但没有被撞断,中柱正上方节点只有较小损伤,结构经过小幅振动后达到新的平衡(试件FM500-V15);第二种情况中柱断裂位置在撞击点,撞击侧的梁端在下翼缘处开裂,框架梁依靠轴拉力发展悬链线效应(试件FM500-V20,FM500-V25,FM500-V30);第三种情况中柱除撞击点外,柱正上方节点也开裂(试件FM500-V35)。图14给出不同速度下的部分结果。 图14 不同撞击速度下的结构响应Fig.14 Structural response for different impact velocities 由位移时程曲线(见图14(a))发现,由于第一种情况中柱正上方节点及相邻梁损伤最小,剩余结构稳定后的位移较小,约为260 mm;第二种情况的三个试件只在梁端下翼缘开裂,稳定后的位移大小接近,约为700 mm;第三种情况的试件接近于倒塌状态,失效点的位移接近1 000 mm。由撞击点位置的撞击力时程曲线(见图14(b))发现,试件FM500-V15的曲线包含峰值段、平台段和下降段;而当撞击块速度大于20 m/s时,中柱在峰值段被撞断,所以随着撞击速度越大,撞击峰值段时间越小。 第2组模型中撞击块的速度为20 m/s,质量从300 kg逐渐增大到900 kg,典型破坏模式如图15所示。撞击块质量小于500 kg的试件,撞击块撞到中柱后被弹回,比如试件FM300-V20和试件FM400-V20,前者受撞击后中柱屈曲,后者受撞击后中柱在撞击点处开裂,但没有被撞断;撞击块质量大于500 kg的试件,撞击块撞断中柱随后撞向防撞桶,比如试件FM600-V20。不同质量试件的部分模拟结果,如图16所示。 图15 不同撞击质量下的破坏模式Fig.15 Failure modes under different impact masses 由图16(a)得到,中柱没有被撞断的情况下,框架在中柱正上方的位移均小于在直接拆柱法后的位移,比如试件FM300-V20受撞击稳定后中柱位移为180 mm,试件FM400-V20中柱开裂后的稳定位移为358 mm;中柱被不同质量撞击并撞断的情况下,各试件正上方节点的位移在750 mm附近,为直接拆柱法结果的1.6倍。由图16(b)得到,试件受撞击持续时间随撞击块质量增大而减小。需要注意的是,中柱被撞断前后的撞击力大小随质量变化的幅度远小于柱被撞断前。由图16还发现试件一旦被撞断后,试件的动力特性随撞击质量变化不大,说明传统直接拆柱法也可以反映撞击去柱后的特性,只是结果偏于保守,需要结合具体灾害乘以放大系数。 图16 不同撞击质量下的结构响应Fig.16 Structural response for different impact masses 第3组试件同时改变撞击块的质量和速度,撞击动能维持在100 J,部分模拟结果如图17所示。各试件在相同撞击动能作用下得到稳定时位移为750 kN左右(见图17(a)),说明撞击曲线平台段的动力特性与撞击能量密切相关。撞击时间与撞击能量呈现不明显规律变化(见图17(b)),比如试件FM274-V27有最大速度却有最短撞击时间,而最小速度试件FM617-V18的撞击时间居于中间。结合上文撞击块速度和质量分析,撞击力的作用时间均随速度和质量的增大而减小。相同动能使撞击块的质量和速度呈不同方向变化,引起撞击力变化规律不明显。 图17 不同撞击动能下的结构响应Fig.17 Structural response for different impact velocities 本文以平面框架受撞击荷载为例,分析具体灾害对框架结构抗倒塌性能的影响,并将撞击结果与传统直接拆柱法结果对比,研究剩余结构的抗倒塌性能,主要结论如下: (1)撞击力和最大位移是动力分析的两大要素,撞击力处于峰值段时,钢梁在撞击点的位移较小,还来不及变形,钢梁最大位移发生在撞击力的平台段。 (2)针对撞击曲线的峰值段、平台段和下降段,提出一种撞击力简化模型。将撞击力简化为简单脉冲后,分析结构体系在各脉冲作用下的激励反应。 (3)撞击拆柱法使节点应力分布复杂,撞击的作用范围会超过被撞柱的范围,引起相邻节点和构件损伤,使柱失效后剩余结构的受力方式和破坏模式发生变化。传统直接拆柱法没有考虑节点破坏,低估剩余结构的动力响应。抗倒塌分析在条件允许下最好结合具体灾害研究。 (4)撞击后的动力特性与撞击能量密切相关,受撞击速度影响最大。撞击力作用时间分别随速度和质量呈反向变化,撞击力时程曲线平台段荷载值由撞击能量确定。
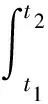
2.3 结构体系对撞击力激励的反应

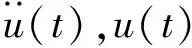

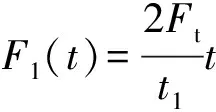

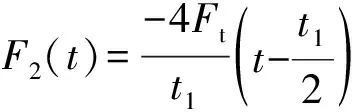

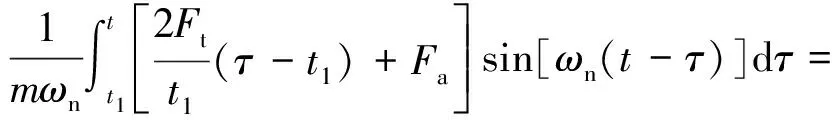
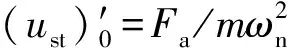
2.4 撞击拆柱法模拟

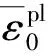

3 撞击拆柱法与直接拆柱法对比
4 框架撞击响应分析

4.1 撞击速度

4.2 撞击质量
4.3 撞击动能
5 结 论

