课堂因“意外”而精彩
江苏省兴化市楚水实验学校 袁小强 (邮编:225799)
课堂的预设是指教师为了有效地开展课堂教学,完成计划中的教与学的任务,教师对课堂中即将发生的活动计划达成的目标进行预先的设计与勾画.事实上,教师在实施课堂教学时,经常遇到一些“意外”,也就是教师课堂预设之外,而这种意外往往是在建构数学概念之前,也是新知识生成之时,教师要善于抓住这样的“拐点”,将“节外生枝”变成“意外的精彩”,教学原本就是即席创造,这样让课堂变得有趣,充满对智慧的挑战和对好奇心的刺激,使师生的生命力得到充分发挥、张扬.
1 课堂意外生成
上新授课《抛物线的标准方程》,在探究抛物线的定义时,给出一个数学小实验,提问:从做的数学小实验中,你发现了哪些关系?生 1:PF+PA=定值,这是一个意外,原来设想学生可以很快找到PF=PC,从而轻松得到抛物线的定义.既然学生提出了,也可以探究一下,先不打算调整学生的思路,尝试一下是否可以走下去,追问:和为定值,前面貌似研究过,应该是什么曲线?学生小声地说:椭圆.继续追问:是椭圆吗?但画出来是什么?学生回答:抛物线.质疑:那怎么矛盾了啊?哪里出问题了?
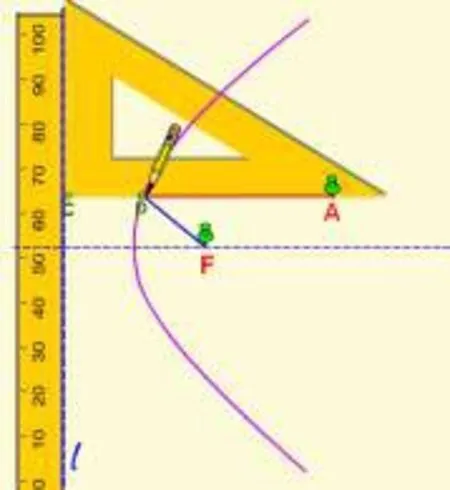
2 引发师生研讨
学生在沉思,激发了学生的学习兴趣.师:带着这个问题,重新回看一下刚刚看的数学实验,小组讨论一下.生2:A点也在动,不是椭圆,椭圆定义是到两个定点的距离,F点是定点,A点是动点.师:很好,现在发现和椭圆的定义不矛盾了,可以继续研究抛物线的方程吗?刚刚同学已经找到了关系:PF+PA=定值,但是点A在动,还能继续研究吗?
3 摸着石头过河

生3:可以研究,虽然A点在动,但是A点在一条定直线上.师:既然可以继续研究,尝试一下,要研究抛物线的方程一般步骤是什么?生4:建系,设点,列式,代点,化简.师:很好!怎么建立合理的平面直角坐标系呢?生4:显然以抛物线的顶点为原点建立,这样抛物线的方程最简单.师:很好!那就按照你的方式建系.要研究P点轨迹,先设一些已知量,设PF+PA=2a,F点是定点,可设为F(c,0),A点在定直线x=m上,大家自己尝试研究一下P点的轨迹方程.生5: 设P(x,y),由PF+PA=2a,可 得移 项 平 方 化 简.师:很好!生 5:平方.师:能直接平方吗?生4:大于零才能,有绝对值,先去绝对值,分类讨论.当x≥m时,要 保 证 2a+mx≥0,也就是m≤x≤m+2a时,平方化简得y2=(2c-4a-2m)x+(2a+m)2-c2,当x<m时要保证x+2a-m≥0,也就是m-2a≤x<m时,平方化简 得y2=(4a-2m+2c)x+(2a-m)2-c2,综上:当m≤x≤m+2a时,P点的轨迹方程为:y2=(2c-4a-2m)x+(2a+m)2-c2,当m-2a≤x<m时,P点的轨迹方程为:y2=(4a-2m+2c)x+(2a-m)2-c2.师:很好!这样我们画出的图形是抛物线吗?生6:显然不是,由于m、a是定值,x的范围是[ ]m-2a,m+2a也定了,而抛物线是可以无限延伸的.师:非常好!为何出现这种状况?生6:绳子长度定了,有限制.师:这样研究有局限性,和我们抛物线图形不符合,我们可以换个思路来研究P点的轨迹方程吗?
4 回到问题本身
师:我们回头继续再来看题目:除了PF+PA=定值,还有其他关系吗?生7:CP+PA=定值.师:找到两组等量关系,怎么研究P点的轨迹更方便呢?生7:PF=CP.师:为什么这样研究更方便呢?生7:F点是定点,C点在定直线l上.师:刚刚生2也说F点是定点,A点在定直线上,一样吗?生7:不一样,刚刚是和为定值,现在是等量关系,化简更简单.师:很好!化简是更简单些,还有其他理由吗?生8:定值有限制,PF=CP无限制,刚刚研究的只能在[]m-2a,m+2a,现在可以跳出绳子的长度限制条件.师:生8用了个“跳出”,很好!这样我们和A点没关系了,只需满足PF=CP,你想象一下,这样的点是不是可以无限延伸?接下来我们研究抛物线的方程.生9:以抛物线的顶点为原点建系,设F(c,0),则直线l:x=-c,设P(x,y),由PF=CP,得师:需要取绝对值分类讨论吗?生9:不需要,直接平方化简得y2=4cx.师:很好!大家比较一下以上两种方法,哪种研究抛物线更方便?生:第二种.师:大家现在可以给出抛物线的定义吗?生10:PF=CP,也就是到一个定点和到一定直线距离相等的点的轨迹是抛物线.师:很好!生10不仅用数学符号语言刻画了抛物线定义,同时还用自然文字语言刻画了,记得研究椭圆和双曲线时有限制条件,那么你认为抛物线需要补充吗?生11:定点不能就在定直线上.师:如果定点在定直线上时,轨迹是什么?生11:过点F垂直于直线l的直线.
5 生成核心概念
师:很好!现在可以给出抛物线的定义:平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.我们把焦点到准线的距离记作p,那么以上抛物线的标准方程就为:y2=2px.问题:在建立椭圆、双曲线的标准方程时,选择不同的坐标系我们得到了不同的形式的标准方程.抛物线的标准方程有哪些不同的形式?请大家自主完成.(利用时间,制作几何画板)
6 辨析释疑解惑
这时,生1有点疑惑,明明画出的图象是一样的,怎么表达式不一样还分段呢?师看出生1的表情:生1还有什么疑惑呢?生1:虽然绳子是有限制的,感觉图象在绳子范围内应该是一样的,所以表达式也一样,为什么不一样呢?师:既然生1有疑惑,有同学可以帮忙解决一下吗?我们先研究当m-2a≤x<m时,P点的轨迹方程为:y2=(4a-2m+2c)x+(2a-m)2-c2的 情 况.生12:刚刚我们把量换了,c用表示的,得y2=(4a-2m+p)x+(2a-m)2-()2,a、m、p好像有关系.师:很好!大家结合图形思考一下a、m、p有关系吗?生13:我发现了,PF=CP,那么2a=m+,代入上式就得到:y2=2px,和抛物线方程一样.师:非常棒!三个量a、m、p其实它们有2a=m+这个等量关系,通过代换消元就可以得到y2=2px,但是仅限于m-2a≤x<m,也就是直线x=m的左侧,其实P点也可以在x=m的右侧,只要保证PF+PA=2a,大家用类似的方法处理一下.生1:当m≤x≤m+2a时,P点的轨迹方程为:y2=(2c-4a-2m)x+(2a+m)2-(c)2,由 于c<m,所 以x的系数2c-4a-2m<0,也是抛物线,不是标准方程.师:非常好!你能猜想一下抛物线的开口方向吗?生1:向左.师:直线x=m的左侧时轨迹是抛物线开口向右,直线x=m的右侧时轨迹是抛物线开口向左.生1:是一个封闭的曲线.师:很好!这是我们刚刚的猜想,我们用几何画板验证一下我们大家的猜想.
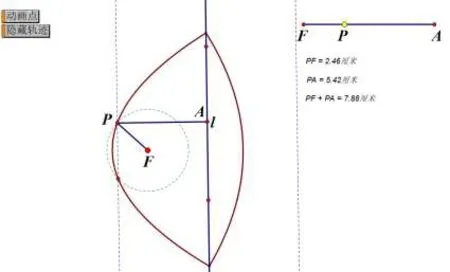
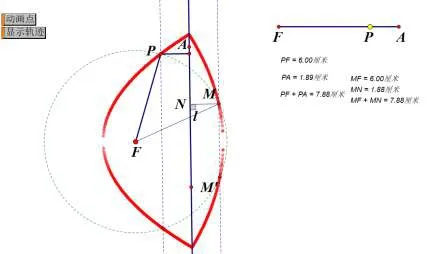
教师展示动画过程,思考:现在,你又有什么发现?和上面的代数研究有区别和联系吗?生1:我终于明白了.由于绳子长度是定值,所以图象有限制,是个封闭的图形,是又两个抛物线构成的,分别在直线的两侧,我开始没发现直线右侧也有图象.
7 “意外”拓展思维
师:生1给了大家一个新的思考方向,新的视角,你是怎么想到的?生1:前面将来到两定点距离之和,差的绝对值为定值,分别是椭圆和双曲线,这里是到定点和定直线距离之和为定值.师:生1用的是类比的方法来研究的,我们还能提出哪些问题可以研究呢?生13:到定点和定直线距离差的绝对值为定值.师:很好!前面我们研究的是到两个定点距离和、差为定值,我们还可以研究?生:积、商.师:非常棒!两个定点距离之比为定值,只要不是1,就是前面研究的阿波罗尼斯圆,当然还可以平方和、平方差、立方和、立方差,两点除了可以研究距离还可以研究什么?生14:斜率,向量.斜率的和差积商、向量数量积为定值等等.生14:两个定点还可以变为定点和定直线,到到定点和定直线距离之积、比、平方和、平方差为定值等等.师:太厉害了!有兴趣的同学课后可以仿照研究椭圆、双曲线、抛物线方程的方法尝试着研究它们的轨迹方程.
8 课堂“意外”的反思
8.1 “意外”发展学生的高阶思维能力
高阶思维是指发生在较高认知水平层次上的心智活动或认知能力,这种思维能力是创新能力、问题解决能力、决策力和批判性思维能力的核心.从学习内容角度看,数学课堂教学是高阶思维培育的主阵地,必须将高阶思维的培育融于日常的数学教学中.从教与学的方式角度看,培养高阶思维,需要采用探究性学习、合作学习、小组讨论等方式,需要提供以学习者为中心的环境,营造情境化的学习氛围,展现基于过程的教学模式,注重知识生成和批判性思维的运用等.通过对问题的思考、探究、比较,对抛物线定义的辨析,发展学生的判性思维性思维能力.
8.2 “意外”发展学生的深度学习能力
美国心理学家布鲁纳说:“最好的动机莫过于学生对所学材料本身内在的兴趣,有新发现的自信感.”学生可以用自己的“发现”作为最高奖励而推进学习的过程.“深度学习”是学习者学习新知识发展过程中,学会迁移学习知识,运用学习知识分析、解决问题,并在学习过程中不断提升发展自身学习能力和素养的过程.学生在课堂上提出新的想法思路是,教师应当顺势引导学生思维,经过大家热烈的讨论,思维碰撞,不断探究、质疑、补充、完善,最后得出抛物线的定义,概念教学应当借助知识的生成过程促使学生学会思考,让学生学会学习,从而实现新课程倡导的“一切为了学生”的核心理念.
8.3 “意外”发展学生的主人翁意识
课堂教学过程超出了教师的预设,但这才是课堂的精彩之处,让学生成为课堂的真正的主人,让学生充分发挥主观能动性,积极提出问题,主动参与探究,合作交流,学生在学习过程中实现再创造的过程,使学生的潜能和创造性得到发挥,培养了学生对自己的信心,喜欢去积极探究,刨根究底,会用数学的眼光观察世界,会用数学的思维思考世界,会用数学的语言表达世界.

