高一“挖坑” 高三“填埋”
浙江大学附属中学丁兰校区 陈作国 施刚良 (邮编:310021)
2019年1 月杭州市高三一模第19题,给高一的学生当做期末复习题来做,应该也可以,而且得分率也还不错.笔者今年教高三,高一的时候就给学生练过,两个班做出来的同学还是蛮多的.高一的时候就可以“做出来”,经过两年的学习和复习,到了高三(2019年1月,笔者教高三),在模拟考中考一下,居然“做不出来了”.这是一件很奇怪的事情,其实也见怪不怪.这与老师的教和学生的学有很大的关系,学生在高一没有把问题订正或理解透彻,指望靠后面的复习将问题搞懂,往往是一厢情愿.高一为自己挖的“坑”(这是数学核心素养没有落实到位所造成的“坑”,就像一颗“定时炸弹”),终究是要自己来“填”的,不然掉进去的最终还是自己.
1 试题呈现
设函数f(x)=
(Ⅰ)若k=1,解方程f(x)=0;
(Ⅱ)若关于x的方程f(x)=0有四个不同的解,求k的取值范围.
注第Ⅰ题略,本文主要探讨第Ⅱ题.
参考答案依题意0有4个不同的解,而x=1是其中1个解,所以只需要考虑方程只有3个解.
评注参考答案的方法是巧妙地将(x-1)2写成|x-1|2,从而提取公因式|x-1|避免分类讨论,再通过参变量分离整体考虑函数图象的位置关系,有一种行云流水的感觉.参考答案学生想不到的主要原因是:将(x-1)2写成|x-1|2,其实这个变形在初中就学过,在高一教师还会再强调的,但学生可能还是不会灵活运用.这说明学生的代数变形能力不强,转化思想欠缺,逻辑推理、数学运算素养不高.
2 解法探究
如图1,当相切时k=-4,两个图象有2个交点,所以要使得两个图象有3个交点,k的取值范围为k<-4.
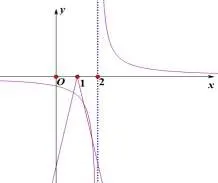
图1
后来又有学生利用另外形式的参变量分离法(将变量与参数彻底分类):

图2
评注在批卷的过程中,这样做法的学生不多,即使有学生画的图象也是不准确的.通过参变分离来解决方程根的问题,学生们是非常喜欢的.因为这样可以避免分类讨论,而分类讨论是学生处理方程或零点问题的“软肋”.这样处理的人数不多主要是:绝对值去掉要分类,也就是说整体的图象是几段图象拼起来的;还有就是分母是两次的分式函数,对学生很有挑战;两条渐进线也往往没有注意到.由此可见学生画图能力和分类讨论能力还有待进一步加强.综合上面的分析,这种图象没画出来,说明学生在高一学习时,对反比例函数与二次函数的复合的性质(先考虑定义域,再研究对称性或单调性,这是研究函数图象的固定“套路”)没掌握,这对以后研究更复杂函数的性质是有一定影响的.更深层次的原因是学生的直观想象、逻辑推理、数学运算素养不高所造成的.
上述方法都是通过转化(主要想法就是参变分离或图象的位置关系),将问题变得易于解决,这是高一讲基本初等函数时惯用的思想方法.难点就是怎样通过分类讨论和数形结合将问题解决.笔者在阅卷时,还发现有学生(这样做的同学很多,这也是学生朴素的想法:看到方程就想解出来)是通过直接解方程做的,尽管过程略显繁琐,但利用方程的思想解决问题也不失为一种途径.
(1)当k>0时,因所以方程①的解为只有一解;因所以方程②无解.故k>0不符合题意.
(2)当k<0时,因所以方程①的解为两解;因x=所以方程②只有一解,故k<0符合题意.
因此,综上所述,k<-4.
评注这种解法尽管学生很容易想到,或多或少都能写一点,但真正能做出来的不多.主要原因还是要对有解的情况加以分类,通过k的范围进行分类,对解进行筛选来确定个数,而不是简单地将之解出就完事,这对学生的思维有较高的要求.对这种问题处理的思想方法,学生在高一都碰到过,关键还是没有将之消化吸收.其实,如果再进一步观察方程①与方程②,我们发现方程①与②的两根之和都为3,而方程②的根要满足x<1,故方程②至多一个解.而方程①与②的解总共要3个,这样只能方程①有2个,方程②只有1个.接下来的思考过程同下述函数观点,此处从略.
如果我们观点站得高一点,从函数思想的角度思考的话,解决起来可能要简洁得多.
因此,综上所述,k<-4.
评注利用函数思想解决方程问题在高一肯定是重点讲过的,学生只抽象理解函数,这样就“只见树木,不见森林”.如果将数与形结合起来,通过直接构造函数,研究函数图象,使得问题的解决变得相对容易,产生一种居高临下的感觉.不在根的解法上纠缠,整体研究函数图象的性质,使得根的分布变得清清楚楚.这样才能真正体现出学生的数学抽象、直观想象、数学建模的核心素养.
3 反思
这道貌似高一学生做的练习题,为什么给高三学生当作模拟题来考,最后考得却不理想呢?笔者谈谈自己的几点想法:
(1)函数思想在高一(乃至整个高中)是非常重要的,学生没有掌握函数思想将影响整个高中数学的学习.教师在具体的教学实践中,没有将研究函数的“基本套路”讲明白,就会导致昏昏的教师教不出昭昭的学生.这也是我们没有将学生的数学抽象、直观想象、数学运算等核心素养没有落实到位的原因.于是乎学生似懂非懂,没有将之消化吸收,到高三复习时不见得就会有好转,所以模拟考一考还是做不来,这也是情理之中的.
(2)方程思想同样在高一(乃至整个高中)是非常重要的,学生对方程朴素的理解就是将之解出来,这样做往往会比较复杂,其实高中阶段的方程主要还是研究方程解的性质或通过韦达定理利用设而不求、整体代换来解决,这对学生的数学思维有较高的要求.能很好地体现学生的数学运算、逻辑推理等核心思想.教师在具体的教学实践中,碰到方程问题时,要引导学生利用函数的观点,将解的性质放到图象中研究,这样可能会使抽象的方程问题形象化,这也是数形结合思想的核心所在.事实上,学生会利用数形结合考虑方程问题,但由于对解的个数情况往往要分类讨论,所以最终又半途而废.
(3)分类讨论思想是学生在高一数学中非常“惧怕”的,这也是学生认为数学难学的一个重要原因,数学中许多有点难度的题目往往都要分类讨论.可以说,分类讨论这种思想的掌握,不可能一蹴而就,往往需要我们在具体问题的解决过程中慢慢渗透,所以在高一练好“童子功”就显得很有必要.要练好“童子功”,分类讨论没有固定套路可走,这就需要学生具体问题具体分析,其实有些“真功夫”就是这样练出来的.正因为没有固定套路,所以学生才认为它难学.难学不是借口,关键还是要掌握分类讨论的标准,这样才会不重不漏.这样才能将逻辑推理、数学建模等核心思想落到实处.
高三复习不是将高一阶段(和高二)的基础知识和思想方法“炒一下冷饭”,但没有高一阶段(和高二)的基础知识和思想方法作为“饭”,想炒出一盘色香味俱全的“饭”也是非常困难的.所以,要使学生能在模拟考试中考出自己的水平,教师必须在高一阶段(和高二)将基础知识和基本数学思想方法渗透到教学实践中,学生能在具体解题过程中灵活地加以运用,师生两方面着力,这样复习阶段的有效性才能凸显出来.“万丈高楼平地起”,只有将高一阶段(和高二)的基础夯实了,高三的复习与模考才能“船到桥头自然直”.

