基于t-SNE加权和的高维多目标优化算法

金 涛，朱 莉，李 豪，汪小豪，姜成龙

(湖北工业大学电气与电子工程学院，湖北 武汉 430068)

高维多目标优化问题是使多个目标在一定条件下尽可能同时达到最佳解的问题，广泛应用于科学研究、金融科技、工程设计的领域，如物资调用、人才分配、工艺设计、生产调度等[1-2]，具有重要的科研和实际价值[3]。随着目标个数的增加，传统的多目标优化算法无法很好的处理高维多目标优化问题，于是人们在传统的算法上进行改进和提升。基于t-SNE的高维多目标优化算法(t-SNE-NSGAⅡ)对目标集进行分析处理，丢弃冗余目标，减少目标维度，降低计算的复杂度，提高算法的收敛性。但其在处理冗余目标集方面，只作简单的删除，使目标集中部分有用的属性可能被丢弃，导致算法的精确度降低。因此利用加权和来拟合冗余目标集，进一步优化初始种群和冗余目标，从而提高算法的准确性。

1 问题分析

虽然t-SNE-NSGAⅡ算法降低了计算的复杂度，提高算法的收敛性，但是t-SNE-NSGAⅡ算法在简化目标集时，损失目标集中有意义的部分属性，导致算法准确性降低。因为在执行t-SNE算法后，对得到的非冗余目标集都直接进行下一次的重新初始化种群操作，导致上次算法中得到的Pareto解集优秀的个体没有保留。这些被舍弃的冗余目标集中存在能够反映目标集的部分属性的优秀个体，并且这些优秀个体能够引导初始化种群的方向，加快算法的收敛速度。

针对t-SNE-NSGAⅡ的不足，提出一种基于t-SNE加权和的高维多目标优化算法(t-distributed stochastic neighbor embedding-weighted sum-non-dominated sorting genetic algorithm with elite strategy，t-SNESUM-NSGAⅡ)，该算法在每次执行t-SNE算法后，不是直接对种群初始化，而是把经过t-SNE算法处理而舍去的所有冗余的目标集拟合成一个新的目标集，再把拟合好的目标集加入t-SNE算法得到的目标集中，最后初始化种群，这样就保留了种群中部分优秀的个体解。因此，t-SNESUM-NSGAⅡ算法既提高了初始种群的质量，也保留了部分种群中目标属性，提高算法的准确性，加快了算法收敛速度。

2 相关工作

按照问题对象的不同，高维多目标优化算法大致可以分为：不含冗余目标问题的算法和含冗余目标问题的算法[4]。第一类算法，是针对不含冗余目标问题的算法，该类算法主要可以从基于松弛Pareto排序方法[5]、基于聚合或分解将多目标整合为单目标问题的方法[6]和基于评价指标的方法[7]三种不同的角度来解决不含冗余目标的问题。第二类算法是针对含冗余目标问题的算法，该类算法主要可以从基于目标间互相关系的目标缩减的方法[8]与基于保持Pareto支配关系的目标缩减[9]的方法两种不同的角度来解决含冗余目标的问题。

随着组成问题的目标个数大幅度增加，高维多目标优化问题变得越来越复杂。不含冗余目标问题的算法，在处理多维目标时，算法搜索能力不足、计算复杂度增加，可视化难度变得越发明显。含冗余目标问题的算法，能够充分挖掘目标之间的相关性，简化目标集的个数，从而降低目标集的复杂度，获得了更广泛的应用。其中,“基于保持Pareto支配关系的目标缩减方法”虽然能够简化目标集，但计算目标集中非支配解集之间的支配关系会增加计算复杂度和计算机设备性能负担。

基于t-SNE的高维多目标优化算法主要从基于目标之间关系的目标方法的角度研究，引入t-随机邻近嵌入(t-SNE)算法来减少高维多目标中存在的目标冗余问题。先通过仿射变换将数据点映射到概率分布上，使高维数据空间和低维数据空间的条件概率差别最小，让数据点从高维空间嵌入到低维空间中，相似度较高的距离较近，而相似度较低的距离较远。然后用KL散度函数作为目标函数来评估嵌入效果的优劣，最后用梯度下降法来最小化目标函数，最终得到收敛的结果。

然而t-SNE-NSGAⅡ算法处理冗余目标集的方式较为粗糙，直接删除冗余目标集可能导致部分有用的属性被丢弃。因此，将冗余目标通过加权和拟合成新的目标集，从而保留目标集中的特征，增强了算法的收敛性，提高了算法的准确性。

3 算法设计

3.1 新目标的拟合

在t-SNE-NSGAⅡ算法中，每次执行t-SNE算法后，得到的目标集中剔除了冗余目标(图1)。

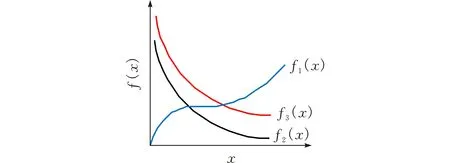
图 1 f1(x)、f2(x)、f3(x)关系分布

图1中f2(x)和f3(x)比f1(x)和f2(x)、f1(x)和f3(x)更为相似，那么通过t-SNE算法计算后，f2(x)和f3(x)的相似度更高，是一对冗余目标，丢弃了f3(x)。f1(x)和其它目标相似度最低，保留下来。

经过t-SNE算法丢弃的冗余目标，只和非冗余目标相似，并不是完全一致。在现实研究、工程问题中，不会存在完全的冗余关系，如果丢弃一个相似的目标，对测试的结果会产生一定的影响。因此，在t-SNESUM-NSGAⅡ算法中，考虑每次经过t-SNE算法中直接丢弃的目标，将这些被丢弃的冗余目标进行加权和，重新拟合成一个新的目标。因为每次t-SNE算法丢弃的目标与保留下来的非冗余目标具有很高的相似度，所以改进后的算法采用平均加权的方式来拟合一个新的目标。设丢弃了n个目标，则拟合后的新目标按照向量{1/n,1/n,…,1/n}进行加权求和。

3.2 t-SNESUM-NSGAⅡ算法流程

传统的t-SNE-NSGAⅡ算法主要的流程为NSGA-Ⅱ→t-SNE→NSGA-Ⅱ→t-SNE这样的循环过程，每次进行t-SNE算法后都丢弃了冗余目标。t-SNESUM-NSGAⅡ算法对t-SNE-NSGAⅡ进行改进，每次t-SNE算法丢弃冗余目标时，对冗余目标集进行加权求和，拟合成新的目标集并参与NSGA-Ⅱ的优化，具体的算法流程见图2。

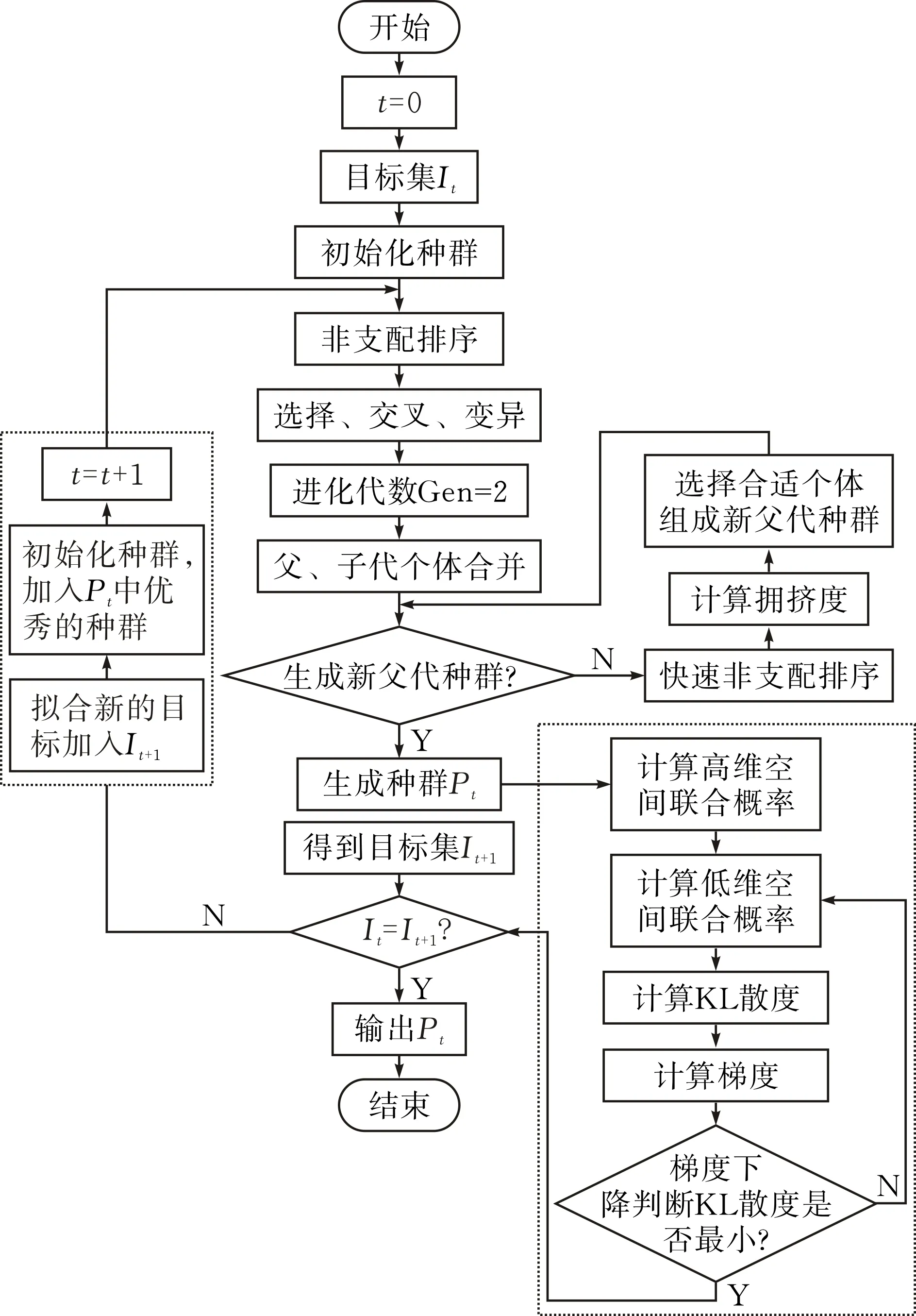
图 2 t-SNESUM-NSGAⅡ算法流程框图

首先，选取原始的目标集I0，对目标集初始化种群，然后执行NSGA-Ⅱ算法优化种群，组成新的父代种群P0；再对P0进行t-SNE算法优化，得到冗余目标集和非冗余目标集，对冗余目标集进行加权求和，拟合成新的目标集，与非冗余目标集合并成重组目标集；最后重复上述步骤，直到满足设置的最大迭代次数，得到种群P2,P3,…,Pt-2,Pt-1，Pt和目标集I3,…,It，It+1，当It=It+1，求出目标集的 Pareto最优解Pt。t-SNESUM-NSGAⅡ算法具体步骤见表1。

表1 t-SNESUM-NSGAⅡ算法

4 实验设计与结果分析

4.1 测试函数

目前，通常选用DTLZ系列测试函数作为高维多目标优化算法领域的测试函数，其中包括DTLZ1-DTLZ7。DTLZ系列测试函数一般可以分为含冗余目标的测试函数和不含冗余目标的测试函数。对于第一种测试函数，选择DTLZ2用来测试算法能否降低不含冗余目标集的目标个数。对于第二种测试函数，选择DTLZ5用来测试算法对简化目标的可行性。

4.2 测试指标

多目标优化算法中有多种性能评价指标：1)收敛性：评价解集与真正的Pareto最优面的趋近程度，具体的评测指标有世代距离(Generational Distance, GD)；2)分布性：评价解集的多样性和均匀分布程度，具体的评测指标有空间评价方法(spacing metric，spacing)、空间分布度(diversity metric, DM)、覆盖率指标(set coverage, CS)；3)综合性能：综合考虑解集的收敛性和分布性，具体的评测指标有逆世代距离(Inverted Generational Distance, IGD)、超体积指标(Hyper Volume, HV)。分别选用世代距离(GD)和空间分布度(DM)来测试t-SNESUM-NSGAⅡ算法准确性和收敛性的优劣。

世代距离评价GD指的是解集P中的每一个点到参考集P′中的平均最小距离，表示偏离真正最优边界的程度。GD的值越大，偏离真正最优边界越远，收敛性就越差。

空间分布度DM表示所获得解集的广泛程度，DM值越小，说明解集越均匀。

4.3 实验参数设置

实验使用的硬件环境为Intel Xeon(R)CPU ES-2620 v4 @ 2.10GHz，Nvidia Quadro M4000 GPU，运行内存为32G。实验在Matlab仿真上实现。为了测试在不同目标个数下，算法性能的好坏，分别设置测试函数中目标个数为3，5，10。DTLZ(I,M)表示目标在I维上的空间分布情况，I为目标维度，M为目标对象个数。具体参数如表2所示。

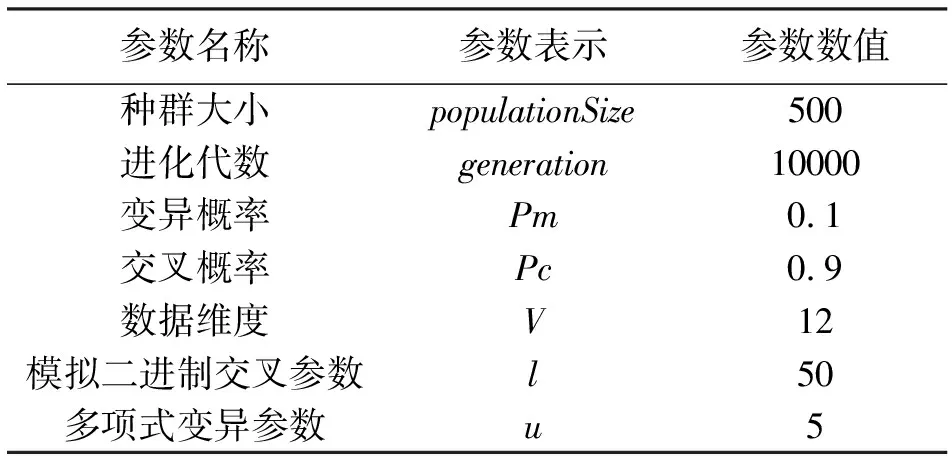
表2 实验设置参数

4.4 实验分析

采用DTLZ2和DTLZ5测试函数，在12维度时，分别选取目标集的个数为3、5、10，采用NSGA-Ⅱ算法、t-SNE-NSGAⅡ算法、t-SNESUM-NSGAⅡ算法实验测试结果，通过实验结果对比验证t-SNESUM-NSGAⅡ算法的收敛性、准确性。

4.4.1DTLZ2(12,3)实验结果与分析采取DTLZ2函数进行对比实验，选取3个目标，算法运行后的目标集与原来的目标集相同，DTLZ2(12,3)的Pareto前沿见图3。说明t-SNESUM-NSGAⅡ算法和t-SNE-NSGAⅡ算法一样不能对不存在冗余目标的目标集进行目标降维。

图 3 DTLZ5(12,3)的 Pareto 前沿图

4.4.2DTLZ5(12,3)实验结果与分析采取DTLZ5函数进行对比实验，选取3个目标，迭代次数为10000，分别运行NSGA-Ⅱ算法、t-SNE-NSGAⅡ算法和t-SNESUM-NSGAⅡ算法，得到DTLZ5(12,3)实验结果见图4。从图4可以看出 t-SNESUM-NSGAⅡ算法和t-SNE-NSGAⅡ算法都具有将目标降至2维的能力。

图 4 DTLZ5(12,3)实验结果图

对DTLZ5(12,3)函数分别用NSGA-Ⅱ算法、t-SNE-NSGAⅡ算法、t-SNESUM-NSGAⅡ算法进行测试，独立运行10次，测试指标取GD和DM，实验结果见表3。

表3 DTLZ5(12,3)测试指标性能比较

由表3中的数据可知，t-SNESUM-NSGAⅡ算法的 GD 和 DM 两个指标的分别为：6.1831E-05，0.5699；t-SNE-NSGAⅡ算法的 GD 和 DM 两个指标的分别为：1.3510E-04，0.4013。由于t-SNESUM-NSGAⅡ算法的GD比t-SNE-NSGAⅡ算法和NSGA-Ⅱ算法GD都小，表示t-SNESUM-NSGAⅡ算法偏离真正最优边界最小，收敛性最好；而t-SNESUM-NSGAⅡ算法DM比NSGA-Ⅱ算法小，但是大于t-SNE-NSGAⅡ算法的DM，表示t-SNESUM-NSGAⅡ算法的解集广泛程度介于两个算法之间。

综上所述，t-SNESUM-NSGAⅡ算法收敛度比NSGA-Ⅱ算法和t-SNE-NSGAⅡ算法更好，解集分布度相对NSGA-Ⅱ算法提高了，但是对于t-SNE-NSGAⅡ算法来说却降低了。t-SNESUM-NSGAⅡ算法收敛速度得到了加强，但是在解集的分布来说反而降低了，这说明t-SNESUM-NSGAⅡ算法虽然得到的解集具有更好的分布度，但是在目标集低的时候解集分布度还是低于t-SNE-NSGAⅡ算法，猜想当目标个数较低时，t-SNESUM-NSGAⅡ算法优势不够明显。

4.4.3DTLZ5(12,5)实验结果与分析采取DTLZ5函数进行对比实验，选取5个目标个数，分别运行t-SNE-NSGAⅡ算法和t-SNESUM-NSGAⅡ算法，得到的DTLZ5(12,5)收敛速度见图5。由上面的结论可以知道，t-SNE-NSGAⅡ算法和t-SNESUM-NSGAⅡ算法都可以把目标降至2维，但从图5可以看出，t-SNE-NSGAⅡ算法大概在迭代次数为6800代左右时完全收敛，而t-SNESUM-NSGAⅡ算法在6400代左右就可以完全收敛，这说明t-SNESUM-NSGAⅡ算法的收敛速度优于t-SNE-NSGAⅡ算法的收敛速度。

图 5 DTLZ5(12,5)收敛速度图

对DTLZ5(12,5)函数分别用NSGA-Ⅱ算法、t-SNE-NSGAⅡ算法、t-SNESUM-NSGAⅡ算法，独立运行10次，测试指标取GD和DM，实验结果见表4。

表4 DTLZ5(12,5)测试指标性能比较

由表4数据可知，t-SNESUM-NSGAⅡ算法的 GD 和 DM 两个指标分别为：1.6389E-03，0.3519；t-SNE-NSGAⅡ算法的 GD 和 DM 两个指标的分别为：2.6509E-05，0.33982。由于t-SNESUM-NSGAⅡ算法的GD比NSGA-Ⅱ算法和t-SNE-NSGAⅡ算法的GD都小，表示t-SNESUM-NSGAⅡ算法偏离真正最优边界最小，收敛性最好；t-SNESUM-NSGAⅡ算法DM比NSGA-Ⅱ算法和t-SNE-NSGAⅡ算法的DM也都小，表示t-SNE-NSGAⅡ算法的解集广泛程度最小。

因此，t-SNESUM-NSGAⅡ算法收敛度比NSGA-Ⅱ算法和t-SNE-NSGAⅡ算法更好，解集分布度相对NSGA-Ⅱ算法提高了，但是对于t-SNE-NSGAⅡ算法来说仍然没有提升。t-SNESUM-NSGAⅡ算法在收敛速度得到加强，但是在解集的分布来说反而降低了，这说明t-SNESUM-NSGAⅡ算法虽然得到的解集具有更好的分布度，但是在目标集低的时候解集分布度还是低于t-SNE-NSGAⅡ算法。

4.4.4DTLZ5(12,10)实验结果与分析采取DTLZ5函数进行对比实验，选取10个目标个数，迭代次数为10000次，分别运行t-SNE-NSGAⅡ算法和t-SNESUM-NSGAⅡ算法，得到的DTLZ5(12,10)空间分布见图6，从图可以看出t-SNESUM-NSGAⅡ算法性能明显优于t-SNE-NSGAⅡ算法。

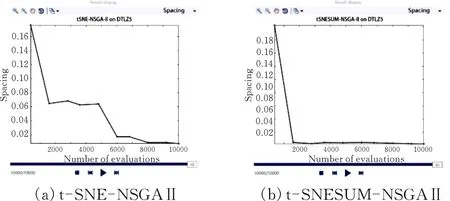
图 6 DTLZ5(12,10)空间分布图

对DTLZ5(12,10)函数分别用NSGA-Ⅱ算法、t-SNE-NSGAⅡ算法、t-SNESUM-NSGAⅡ算法进行测试，独立运行10次，测试指标取GD和DM，实验结果见表5。

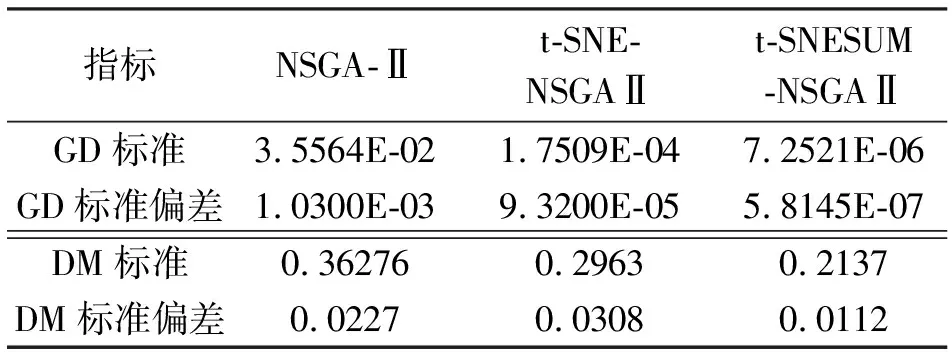
表5 DTLZ5(12,10)测试指标性能比较

由表5中的数据可知，t-SNESUM-NSGAⅡ算法的 GD 和 DM 两个指标分别为：7.2521E-06，0.2137；t-SNE-NSGAⅡ算法的 GD 和 DM 两个指标分别为：1.7509E-04，0.2963。由于t-SNE-NSGAⅡ算法的GD比NSGA-Ⅱ算法和t-SNE-NSGAⅡ算法的GD都小，表示t-SNESUM-NSGAⅡ算法偏离真正最优边界最小，收敛性最好；t-SNESUM-NSGAⅡ算法的DM比NSGA-Ⅱ算法和t-SNE-NSGAⅡ算法的DM也都小，表示t-SNE-NSGAⅡ算法的解集广泛程度最小。

综上所述，t-SNESUM-NSGAⅡ算法无论是收敛到最优边界能力还是解集分布度都明显优于t-SNE-NSGAⅡ算法，验证了随着目标个数的增加，t-SNESUM-NSGAⅡ算法性能比t-SNE-NSGAⅡ算法的更好。

5 结论

t-SNESUM-NSGAⅡ算法在t-SNE-NSGAⅡ算法的基础上进行改进，进一步优化初始种群和冗余目标，提高了算法的准确性。该算法重点在t-SNE分析处理得到的冗余目标集进行拟合形成了新的目标集，并加入下一步的运算中；而且在每次初始化种群的时候，保留父代种群的部分个体。虽然t-SNESUM-NSGAⅡ算法中采用对冗余目标集直接加权和，拟合成新的目标，这样虽然可以保留目标集的部分属性，但大部分属性仍旧丢失。因此在面对冗余目标集时候，如何选择一个好的拟合方法，怎样分配拟合后各个目标集间的权重，来充分挖掘目标集的特征，降低目标维度，还有待进一步研究。