基于5次NURBS的六足机器人足端轨迹规划

周敬东，汪 宇，高伟周，杨 磊

(湖北工业大学湖北省农业机械工程研究设计院，湖北 武汉 430068)

轨迹规划是六足机器人实现行走功能的重要环节。轨迹规划方法有两种：一是在操作空间内，机器人足端行走过的路径比较直观，容易观察，但是该方法未考虑运动的奇异性，运动需要经常计算逆解；二是在关节空间中，通过运动学逆解方程，将笛卡尔空间中腿部所处的位置时间序列与其关节空间中的位置时间序列相对应，该方法对关节的角速度和角加速度有一定程度上的约束，还避免了运动奇异性[1]。

在实际研究中，轨迹规划有多种方法，例如梯形法、正弦法[2]、多项式以及B样条[3-4]等。其中，NURBS(非均匀有理B样条)曲线插值法能保证轨迹规划时角度、角速度和角加速度不发生突变且稳定性良好，轨迹曲线在控制顶点形成的凸状包之内，便于轨迹的控制与关节的约束[5]。

综上所述，已知六足机器人腿部足端首末两端位置，通过机器人逆运动学得到腿部各关节的角度和角速度，再基于5次NURBS曲线插值法进行拟合，得到各关节的角度、角速度以及角加速度曲线，从而实现对六足机器人的足端轨迹规划[6-7]。

1 机器人腿部位姿描述

1.1 机器人腿部正运动学分析

机器人腿部由基节、股节和胫节三部分组成，机器人机体和这三部分肢节分别通过基关节、股关节和胫关节进行连接[8]。对机器人腿部进行正运动学分析，即根据机器人机体的位置和三个关节的角度，计算出腿部足端末点的位置坐标的过程[9]。使用D-H方法在机器人的某条腿上建立坐标系(图1)。机器人腿部的D-H的相关参数如表1所示。

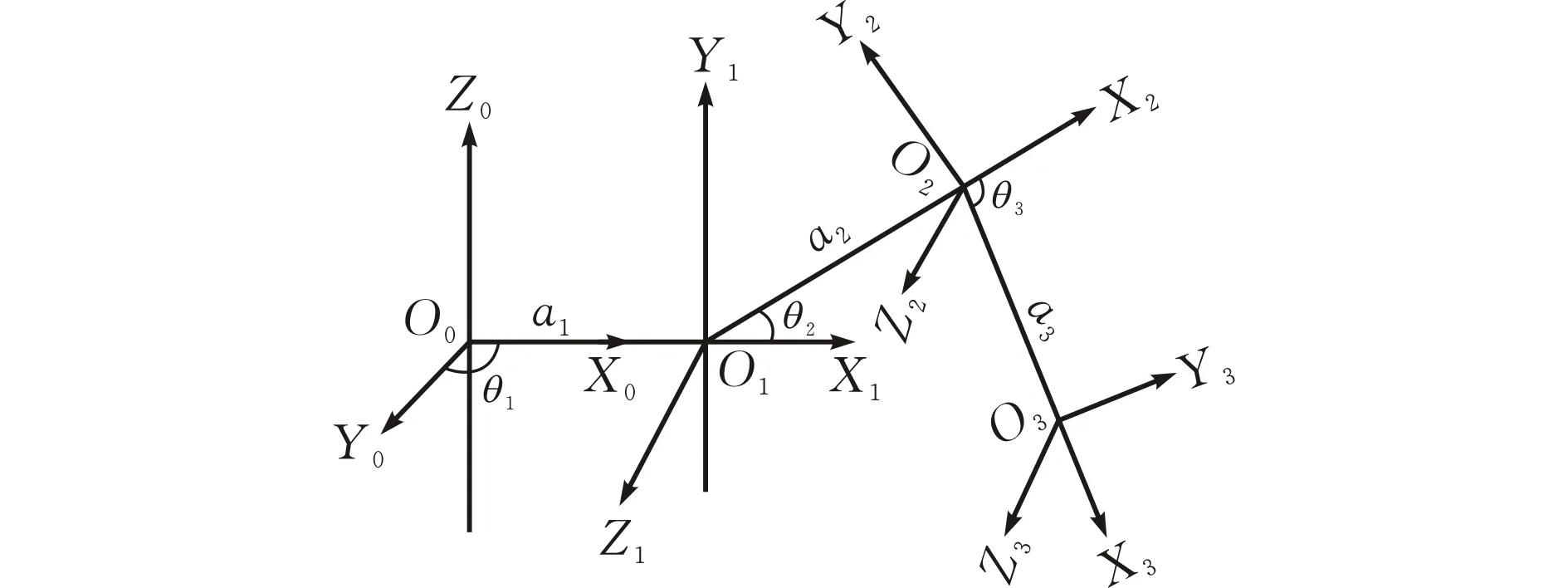
图 1 机器人腿部坐标系

表1 D-H参数

通过代入D-H参数，机器人腿部各关节之间的变换矩

(1)

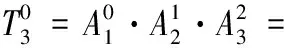
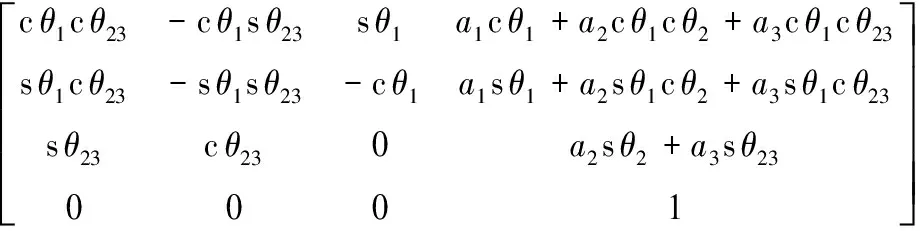
(2)

式中：cθ1=cosθ1，sθ1=sinθ1，sθ23=sin(θ2+θ3)，cθ23=cos(θ2+θ3)。

机器人腿部足端点各坐标为：

(3)

1.2 机器人腿部逆运动学分析

对机器人腿部进行逆运动学分析，根据机器人某条腿足端末点的位置，利用左乘逆变换矩阵，计算出这条腿上各个关节角度的大小：

(4)

(5)

六足机器人的腿部雅克比矩阵和各关节角度的关系为：

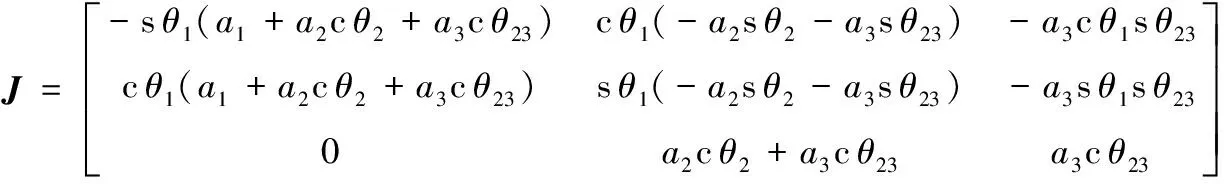
(6)

在求出机器人腿部的雅克比矩阵后，可以通过足端点的线速度来得到腿部各关节的角速度，两者之间的关系为：

(7)

式中，vx，vy，vz分别为腿部足端点在x轴、y轴、z轴的线速度。

2 基于5次NURBS的轨迹规划

六足机器人的足端轨迹规划包含的内容有：根据机器人的运动过程与轨迹，确定相应的轨迹参数，利用MATLAB软件进行模拟和描述；进行相应的计算，求解出机器人足端对应的各关节的角度、角速度和角加速度[10]。本文研究的六足机器人选择在笛卡尔空间中进行轨迹规划，通过机器人逆运动学求解关节空间中的各关节角度，再结合5次NURBS曲线插值法得到关节运动轨迹曲线。

NURBS又称为非均匀有理B样条，它能对曲线进行精确的解析，可快速稳定地计算出相应的结果，所以本文将NURBS曲线设置成机器人腿部关节空间轨迹曲线的插补方法。NURBS曲线可以设置起终点的角速度和角加速度,除此之外，还能进行特定点的优化配置，使其保持连续。表达式为[11]：

(8)

式中：di(i=0,1,...,n)是对应曲线的控制顶点；Ni,k(u)(i=1,2,…,n)是k次规范B样条基函数，基函数可定义为：

(9)

式中：k为NURBS的次数；i为NURBS的序号。u=[u0,u1,…,un+2k]，是k次NURBS轨迹曲线定义域的节点矢量。须对时间节点进行归一化处理：

(10)

式中，Δti=ti+1-ti。将[uk,un+k]区域内的节点应用于插值的n+1个数据点pi的k次B样条曲线方程，得到符合插值条件的相应方程[11]：

(11)

k次B样条需要增加k-1个边界条件。设两端节点重复度为k，B样条曲线的首端和末端的控制点等同于首端和末端的数据点，相应的边界条件为：

(12)

对式(12)的n+k个方程进行联立，就可以解出控制顶点di(i=0,1,…,n)[11],再利用前面的公式进行推演，就可以解出k次B样条基函Ni,k(u)(i=1,2,…,n)，进而解出机器人腿部运动轨迹上每一个点对应的关节位置p(u)，再对得到的NURBS曲线进行求导，最终求解出机器人腿部各关节在运动过程中的角速度和角加速度。

3 仿真及分析

本文所研究的机器人腿部基节、股节和胫节的长度分别为a1=50 mm，a2=70 mm，a3=140 mm。对机器人腿部在关节空间中以点到点的方式来控制轨迹，所经过的机器人腿部足端位置坐标依次为(0，130，-30)、(4，140，-15)、(8，150，10)、(12，160，20)、(16，170，10)、(20，180，-15)、(24，190，-30)。代入六足机器人的运动学模型进行逆解，得到各关节在不同位置时的角度θ1、θ2、θ3。

将整个运动行程机器人腿部足端初始端点、末端点以及求解出来的相应位置的各关节角度通过5次NURBS曲线插值法进行轨迹规划，规定机器人腿部运动的时间为2 s，各关节初始和终止角速度为0。通过MATLAB对机器人腿部进行足端轨迹规划仿真，得到机器人腿部足端在关节空间里的运动轨迹曲线(图2)。腿部各关节的角度、角速度和角加速度随足端在关节空间里位置的变化而发生改变。图3—5为各关节在关节空间内的角度、角速度和角加速度变化曲线[12]。

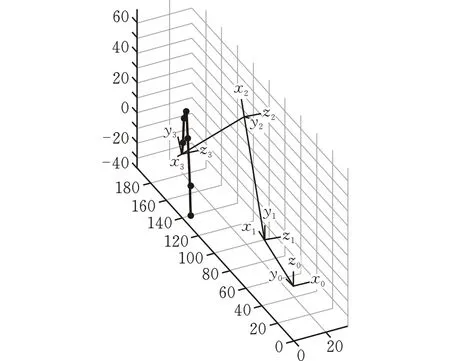
图 2 腿部足端关节空间轨迹

从图2可以看出，机器人足端经过的点的位置与规划的点的位置一致，且轨迹曲线光滑连续，表明5次NURBS曲线插值法能成功应用于足端轨迹规划。由图3—5可知，机器人腿部各关节角度、角速度以及角加速度的轨迹曲线平滑而且连续，在加减速过程中没有产生突变的情况，能使机器人足端稳定着陆，减少了角度变化对腿部产生的冲击，从而有利于实现机器人腿部的平稳以及快速运动。

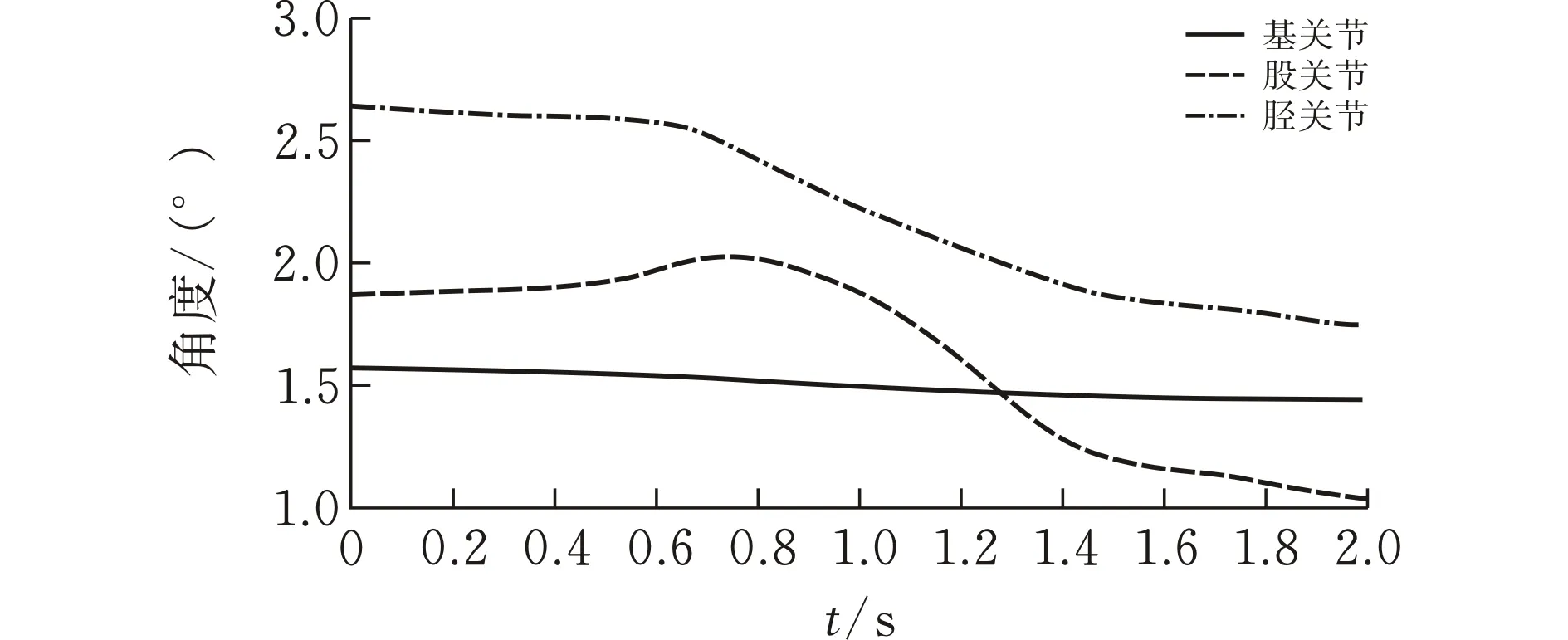
图 3 腿部各关节角度轨迹

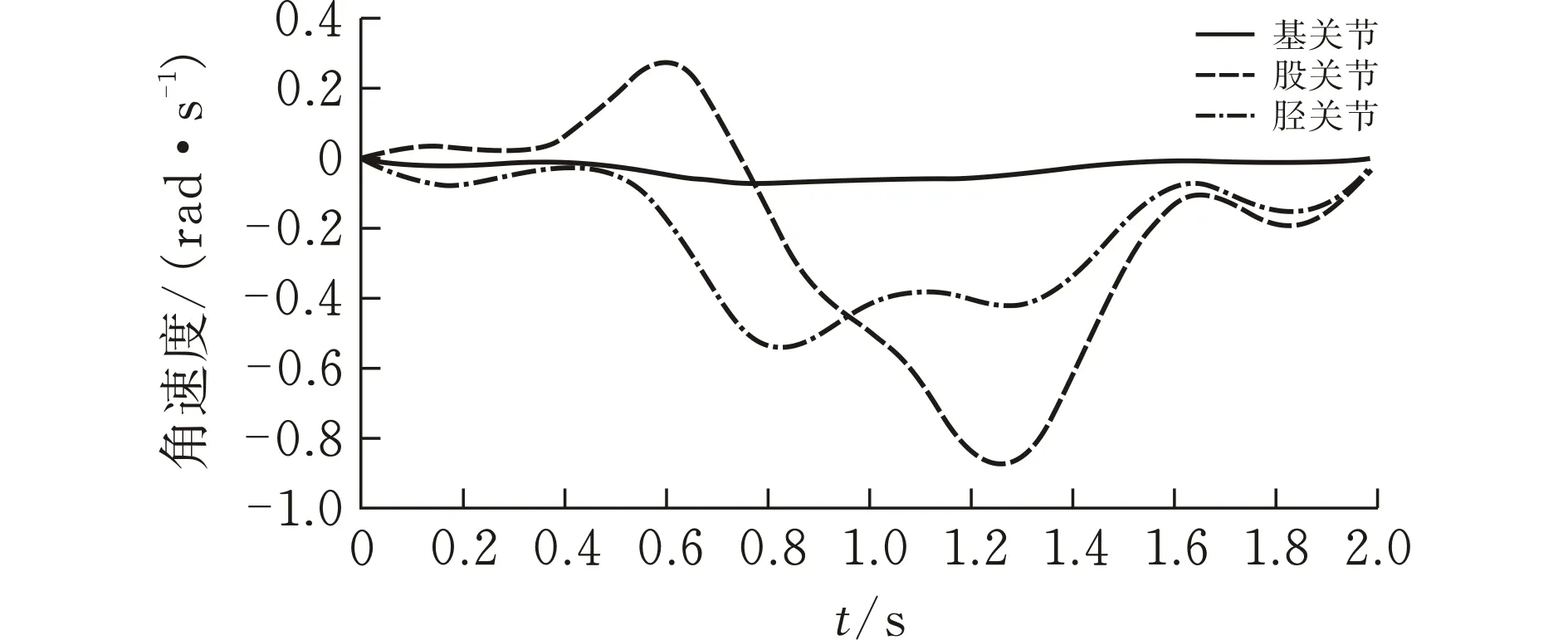
图 4 腿部各关节角速度轨迹

图 5 腿部各关节角加速度轨迹

4 试验

针对基于5次NURBS插值法的轨迹规划，以六足机器人为研究对象，机器人和试验环境如图6所示。设置机器人腿部足端起点为(0，130，-30)，终点为(24，190，-30)，运行时间为2 s.在腿部运动过程中，将规划形成的腿部足端位置信息和时间点输入到机器人控制系统当中，通过上位机导入相应程序代码以控制机器人腿部足端进行轨迹规划，得到机器人腿部在x、y、z方向上的位移曲线。图6为未引入5次NURBS插值法的机器人足端坐标轴方向位移曲线图，图7为引入5次NURBS插值法后的机器人足端坐标轴方向位移曲线图。

图 6 六足机器人

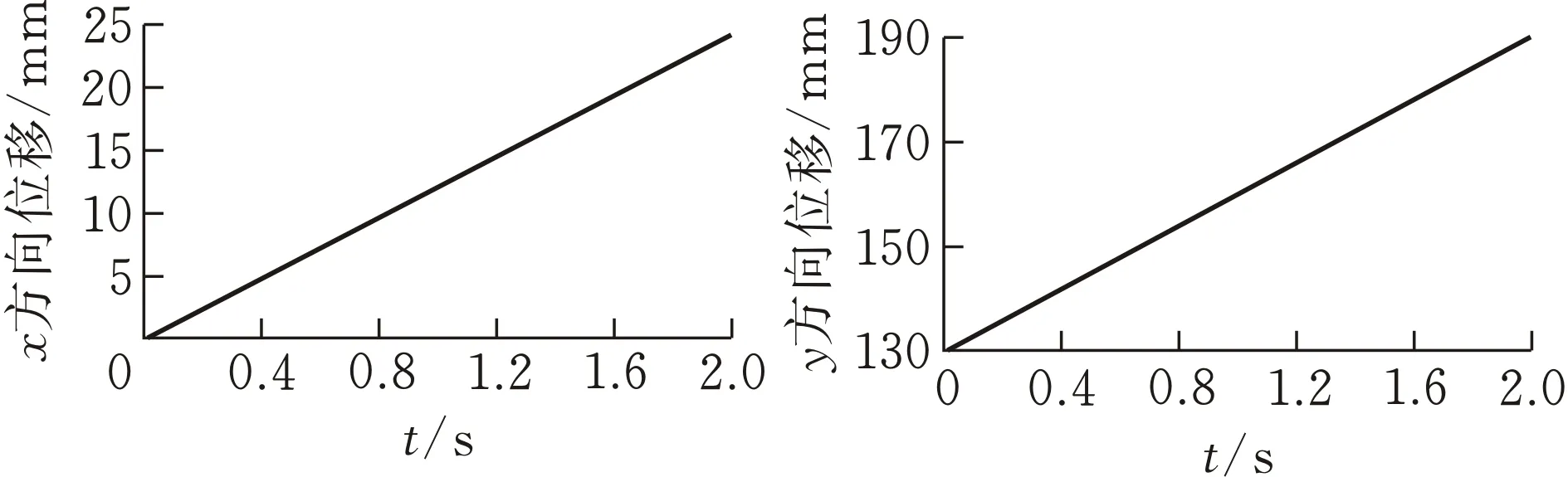
(a)x方向位移 (b)y方向位移

(a)x方向位移 (b)y方向位移

试验结果表明：未引入5次NURBS插值法时机器人腿部运动加减速过程不明显，易产生冲击；引入5次NURBS插值法后，机器人腿部足端在实际运动过程中运动轨迹光滑连续，加速和减速过程明显，使得机器人腿部运动更加平稳，试验结果与仿真结果一致，证明采用5次NURBS插值法进行轨迹规划的可行性。

5 结论

在对六足机器人运动轨迹优化的过程中，为提高机器人腿部运动的稳定性和准确性，本文基于机器人正逆运动学，采用5次NURBS曲线插值法对六足机器人的足端轨迹进行规划。根据机器人腿部足端所处的位置，通过机器人正逆运动学计算，得出机器人抬腿过程中所经过位置的各关节角度以及角速度，再用5次NURBS曲线插值法进行仿真拟合，得到腿部各关节角度、角速度和角加速度变化，再通过试验得到机器人腿部在x、y、z方向上的位移曲线。仿真和试验结果表明：基于5次NURBS的足端轨迹规划的关节角度、角速度和角加速度的轨迹较为光滑，没有出现突变的情况，避免了机器人运动过程中腿部产生振动冲击的情况，试验结果验证了仿真结果的合理性与可行性，达到预期的效果。采用5次NURBS曲线插值法构造的足端轨迹能够使六足机器人腿部运动平稳、动作快速。