高效鲁棒三维结构化重建
潘珊珊,吕佳辉,方昊,黄惠
深圳大学可视计算研究中心, 深圳 518052
0 引 言
“数字孪生”(digital twin)是指通过计算机技术在数字空间中建立各类真实世界物体的虚拟镜像,用于真实世界场景的仿真、模拟和优化等任务,广泛应用于智慧城市、智慧交通、智慧家具、智慧安防和城市规划等领域,具有极高的社会经济价值。其中,如何快速、准确地建立真实世界物体的3维模型是数字孪生技术能否得到广泛应用的重要技术环节。通常情况下,数字孪生技术要求得到的3维模型具有高精度、矢量化、低复杂度、非自相交和水密等特点。在计算机图形学领域,得到3维模型的方式一般分为以下两类。
首先,传统的计算机辅助设计(computer aided design, CAD)几何建模技术发展最为成熟。该技术主要使用基于几何造型的建模方法,由专业美术人员通过使用几何造型软件(如AutoCAD、3DsMax等),运用计算机图形学与美术理论,创建出物体的3维模型。该方法已广泛应用于诸多领域,可解决可视化、仿真和制造等多类任务,然而采用这种建模技术工作量大、周期长、操作复杂、效率低,不适合处理大量数据,并且由于建模过程极大地依赖于建模人员的专业知识与经验,精度无法保证。
其次,3维重建算法作为一种逆向工程技术,其目的是将现实世界中目标对象转化成对应的3维几何模型。现有的方法通过单目相机、LiDAR(light detection and ranging)和RGBD相机等传感器采集真实物体的多源数据,并用相关算法生成对应的3维模型,伍龙华和黄惠(2015)简要介绍了近年来围绕点云的3维重建流程,Kazhdan等人(2006)从点云数据重建3维模型,Barnes等人(2009)基于随机化的算法在两幅图像中寻找匹配区域,Furukawa和Ponce(2010)基于多视角立体视觉从图像中重建模型,Newcombe等人(2011)使用RGBD相机进行实时重建,胡芳侨等人(2020)主要介绍了建筑领域的3维重建现状。然而,如图1(a)所示,现有的大部分基于多视角立体视觉的3维重建方法得到的3维模型依然停留在较低的层次,它们通常包含许多缺陷,比如模型自相交、没有保持应有的连接关系、包含不必要拓扑结构以及缺乏结构化信息等。一方面,由于测量条件的限制,测量数据经常存在严重的噪声;另一方面,现实场景的复杂性也决定了测量过程中不可避免的遮挡问题,因此测量得到的数据通常也是不完整的,存在部分数据缺失的情况,且处理过程过多地依赖于人工交互,增加了模型后续处理的难度和工作量。不仅如此,这类3维模型通常由大量的三角面片组成,缺少高阶几何信息,无法直接用于数字孪生技术的下游领域,例如实时渲染、参数化编辑等。

图1 传统3维重建算法得到的原始模型与本文结构化重建模型Fig.1 Comparison of traditional reconstruction model and structured reconstruction model ((a) traditional reconstruction model; (b) our structure-aware reconstruction model)
因此,现有的3维模型获取方法均无法满足数字孪生技术的应用要求。与一般物体相比,建筑、家具和机械零件等人造物体通常具有较为明显的结构特征,其表面可以看成是由一系列几何平面拼接而成。因此,结构化重建方法,即从离散点云或者原始三角网格数据中提取几何平面并将其拼接成紧凑的参数化3维模型为获得数字孪生所需的3维模型提供了重要解决思路。以往的方法通常面临着两个挑战:1)传统的形状检测方法,例如区域增长算法通常依赖于迭代地选取种子点并判断周围的点或三角网格是否属于种子点所对应的几何形状。这种贪心策略只考虑到物体的局部特征,无法保证整体结果的准确性。2)现有的形状拼接算法利用提取出的几何平面将3维空间切分成一系列的多面体,并判断每个多面体属于物体的内部或者外部以获得属于物体表面的多边形网格。这种方法通常受限于计算复杂度,从而只能处理由一百多个几何平面组成的物体,极大地限制了算法的应用场景。
针对这些问题,本文提出了一种快速、鲁棒的结构化重建算法,可以自动将离散点云或者三角网格转化为紧凑的多边形网格。该方法主要基于以下3个创新点:1)提出了一种多源区域增长算法全局地从原始3维数据中提取特征几何平面。该策略保证了处于两个平面相交处附近的点或者三角网格可以被正确地聚类到所属的平面区域。2)为了避免计算几何平面在3维空间中所有的相交信息带来的计算负担,采用了一种基于二叉空间分割树的结构将3维空间切分为多面体。与传统的全相交空间分割算法相比,通过这个简单并且鲁棒的机制得到的多面体数目和运行时间都降低了至少两个数量级。3)提出了一种基于光线射击的马尔可夫能量方程以提取物体的表面多边形,得到水密、无自相交的多边形网格。本文方法已应用于一系列各式各样的真实世界物体的重建以证明该方法的鲁棒性和快速性。实验结果表明,本文方法在计算效率以及结果的准确性上均取得了较大的进步,并在复杂性和保真度之间提供了一种较好的方案。
1 相关工作
1.1 网格模型简化
网格模型简化法旨在保证整体模型准确性的前提下迭代地减少模型网格数目,包括两类方法:1)基于原始网格模型的边—坍塌简化法;2)基于模型局部几何结构抽象的网格重划分法。
基于原始网格模型的边—坍塌方法迭代地将相邻的两个顶点融合,不断减少三角网格的数量,如Garland和Heckbert(1997)基于二次型误差(quadric error metric, QEM)来确定顶点融合的优先级和融合后新顶点的坐标。然而,基于边—坍塌的简化方法无法保留物体模型的结构特征,例如特征平面及特征边。针对这个问题,Salinas等人(2015)首先从3维模型中提取特征平面,再将特征平面信息嵌入到迭代简化过程中,使得简化之后的模型保有这些结构化特征。Li和Nan(2021)采用相似的思路,通过设计新的误差函数,使得边—坍塌算法可以在简化的过程中保有特征平面、特征边等结构信息。然而这些方法生成的特征平面是由近似共面的面片组成。此外,受噪声、遮挡和离群值等影响,自动化重建真实物体的3维模型比较嘈杂,缺陷较多,这类边—坍塌方法通常要求输入模型有正确的几何拓扑结构,无法修复输入模型本身的缺陷。
基于模型局部几何结构抽象的网格重划分法则忽略原始模型的拓扑结构,生成与原始模型近似的简化模型。Cohen-Steiner等人(2004)通过对面片迭代聚类的方法将输入模型分割成若干个近似平面的区域,然后找出原始模型中的“锚点”,即与至少3个区域相邻的顶点,最后根据“锚点”生成简化模型。Mehra等人(2009)将输入模型以粗分辨率进行体素化,再对体素化模型的表面进行变形以拟合原始模型,体素化步骤的分辨率决定了最终简化模型的拓扑结构。这类方法生成的模型容易存在面片折叠、自相交等缺陷。
1.2 形状检测
建筑、家具和CAD设计模型等人造物体的形状包含大量结构特征(Mitra等,2014),通常由平面、圆柱和球面等规则形状组成,各个几何形状之间存在彼此垂直、平行、共面和对称等关系。从模型中检测结构形状和互相之间的关系是结构化重建的前提。Kaiser等人(2019)总结了从原始稠密数据中提取简单几何形状的算法。常见的形状检测方法有RANSAC(random sample consensus)(Schnabel等,2007)、区域增长(Shamir,2008)和霍夫变换(Chen和Chen,2008;Hulik等,2014)等,这些方法的主要缺点在于烦琐的参数调节。Lu等人(2021)从模型中提取特征曲线网络进而检测形状。Zhang等人(2020)基于马尔可夫随机场(Markov random field, MRF)分割框架分割模型表面进而拟合形状,特别是滚球过渡曲面(rolling-ball blending surfaces)。近年来提出了许多基于数据驱动的形状检测方法,Fang等人(2018)通过有监督学习的方法得到不同LOD(levels of detail)重建等级所需要的平面检测参数,Sharma等人(2020)用神经网络从点云数据中拟合形状参数,Tulsiani等人(2017)用神经网络学习模型的抽象长方体表示,但这些方法需要人工标注数据,或者难以应用到真实数据上。检测出形状后,Li等人(2011)优化形状之间的垂直、平行和对称等关系,以增加对噪声的鲁棒性,但算法复杂度较高,因此,Verdie等人(2015)通过层次化地建立和优化形状之间的关系以提升效率。然而,这类形状检测方法只考虑了局部最优解,使得落在两个相邻形状交界处的点或者三角面片无法被正确地聚类到所属的几何形状中。
1.3 平面形状拼接
平面形状拼接旨在将检测到的平面形状拼接成一个多边形网格,主要包括两类方法:1)连接法;2)空间分割法。
连接法通过建立各个几何形状之间的连接图,分析平面形状之间的相邻关系,确定每个平面的多边形,作为输出多边形网格的顶点、边和面(Mehra等,2009;Chen和Chen,2008)。但是连接图可能丢失应有的或包含错误的连接关系,生成不完整的或错误的模型。一种可能的解决方案是交互式地修复模型(Arikan等,2013),或者自动化地生成密集三角形网格填补缺失的部分(Lafarge和Alliez,2013)。然而,第1种方法难以处理大量数据,第2种方法输出的多边形网格缺乏结构信息,且不满足轻量化的需求。
空间分割法对于具有挑战性的数据更加鲁棒。该方法用检测到的平面形状将3维空间分割成一些凸多面体,然后从分割结果中提取模型表面对应的多边形网格。这类方法主要的难点在于降低空间分割的复杂度。如果直接使用所有平面形状的支撑平面切割包围盒,这种全相交分割法会导致许多冗余分割,占用大量计算时间和内存。更重要的是,从分割结果中提取多边形网格这一步骤的搜索空间大大增加,重建结果更难以保持简洁紧凑的平面特征。为此,Chauve等人(2010)先简单地将包围盒垂直或水平分割成多个子空间,再根据平面形状切割子空间,形成一个二级层次结构。Fang和Lafarge(2020)结合连接关系来降低空间分割的复杂度。空间分割完成后,可以将每个区域标记为模型内部或外部,然后提取内外的边界形成网格模型;或将其转化为带约束的整数线性规划问题,挑选满足要求的面片形成网格模型。Bauchet和Lafarge(2020)通过“扩张—碰撞—停止”的思想将平面形状对空间的分割效果限制在局部范围内,从而减少冗余分割。但平面形状之间的碰撞和分割逻辑非常复杂,这导致高效的碰撞分割算法难以实现。他们提供的算法实现需要判断任意两个平面形状是否可能碰撞,并且需要保证所有潜在碰撞事件的前后顺序,也就是说其计算受到全局空间中所有平面形状的影响。本文算法不仅保证了分割结果的局部性,计算过程也只考虑局部范围的平面形状,因而在保证分割质量的前提下,大幅降低了时间复杂度。
2 算法描述
2.1 算法流程
本文方法整体流程如图2所示。以带法向量的点云数据或者三角网格模型作为输入,输出物体表面对应的水密模型。1)使用多源区域增长算法从输入数据中检测特征平面,并计算特征平面对应的2维凸包(凸多边形);2)利用凸包多边形递归地将对应的3维空间切分成两个凸多面体,建立二叉空间分割(binary space partitioning, BSP)层次树结构,最终BSP树的每个叶子节点对应一个凸多面体;3)建立马尔可夫场模型判断每个多面体属于物体的内部或外部;4)提取所有内—外区域分界面作为物体的表面多边形网格。
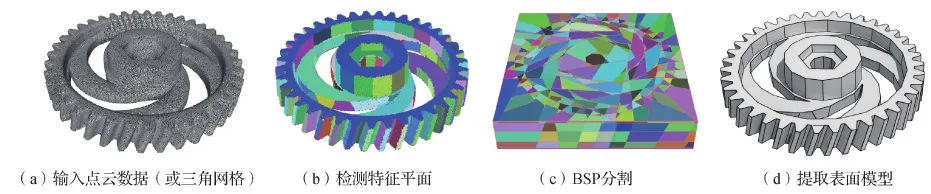
图2 结构化重建流程Fig.2 Structure-aware modeling pipeline((a) point cloud (or mesh) as input; (b) plane shape detection; (c) BSP based partition; (d) surface extraction)
与基于隐式场的3维重建方法类似,将表面重建问题转化为空间的内外划分问题,这样可以保证输出模型水密且无自相交,但与自由曲面的重建算法不同,本文的求解空间限制在BSP树的叶子节点中,重建模型的面片在特征平面的支撑平面中,使得重建结果保留真实世界物体的整体结构上的平面和边角特征。
2.2 特征平面检测
(单源)区域增长算法,作为一种从点云或网格模型中检测特征平面的常用方法,广泛用于结构化3维重建任务。该方法从一个起始元素(一个点或三角面片)位置开始,逐渐向周围扩张,将所有满足一定约束条件的点或者三角面片聚类成该区域对应的几何形状。常见的约束有:待扩张元素的法向量与已有区域的法向量夹角小于ε;待扩张元素的位置与已有区域的支撑平面距离小于δ。当一个区域的所有相邻元素都不满足约束条件时,此区域停止增长,如果此区域大小超过σ,便从中提取特征平面。算法从剩下的元素中检测下一个特征平面,即选择一个新的区域起始位置开始增长。重复上述过程,直到遍历完所有元素。最后用最小二乘平面拟合每个区域,并将区域中所有元素投影到平面上,得到平面结构,这些平面结构是用于后续重建的基础。
区域增长是一种局部贪心算法(Shamir,2008),后续区域的增长要等之前的区域增长结束后才可以开始。对于光滑变化的模型表面来说,由于没有明显边界来触发区域增长的停止条件,每个区域的边界依赖于区域增长的先后顺序,如图3(a)所示,从左至右分别表示从点云中检测到的平面区域、从区域中提取的2维凸包和最后结构化重建的模型。这种迭代式算法影响了处于特征平面边界元素的聚类结果。由于后续需要利用这些检测到的平面结构重建3维模型,更加合理地划分区域的边界有助得到更准确的平面结构,进而得到更好的重建结果。
为了消除区域增长的先后顺序不同对平面检测结果带来的影响,本文采用多源区域增长算法(multi-source region growing, MRG),重新划分区域的边界。这是一种全局贪心算法,同等对待所有区域,区域的增长不再有明确的先后顺序。对于(单源)区域增长检测到的每一个平面区域,MRG从输入数据中挑选与之最近的元素作为这个区域的种子元素。接着将所有种子元素作为起始位置,同时进行所有区域扩张。

图3 多源区域增长前后对比Fig.3 Impact of multi-source region growing ((a) single-source region growing; (b) multi-source region growing)
具体来说,对于每一个起始元素,MRG将相邻元素加入一个全局的优先队列中,元素与支撑平面越近,优先级越高。由于一个元素可能与多个区域相邻,因此优先队列中一个元素可能出现多次。每次从队列中选取优先级最高的元素E和相应区域Ri,若该元素已经被划分到其他区域,则跳过它,从优先队列中取下一个元素;否则,将其加入区域Ri中,并将相邻的尚未划分区域的元素加入队列中。此外,处理队列中元素的时候,如果它不满足夹角约束ε或距离约束δ,则直接跳过这个元素。当优先队列为空时,多源区域增长结束。重新划分后的区域如图3(b)所示,可以看到,不同区域之间的划分更加合理。最后从这些区域中重新提取平面结构,使得重建结果更加准确。
对于点云输入,本文将K个最近点作为相邻元素;对于三角网格模型输入,本文将相邻的3个面片作为相邻元素。
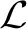
(1)
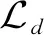
(2)
(3)
式中,nE表示元素E的法向量,np表示平面P的法向量。
算法1:多源区域增长
全局优先队列Q←∅
区域(R0,R1,…,Rk)←单源区域增长
Procedure:选取种子元素
forRi=R0→Rkdo
种子元素E←Ri中与Pi最近的元素
清空Ri中元素
将E加入Ri
将(E,Ri)加入Q
Procedure:增长
whileQ≠∅ do
从Q中取(E,Ri)
ifE不属于任何区域 then
将E加入区域Ri
forE的相邻元素Ejdo
ifEj不属于任何区域 then
将(Ej,Ri)加入Q
2.3 基于BSP的空间分割
为了更加鲁棒地对带有缺陷的输入数据进行结构化重建,采用空间分割的思想,将2.2节中检测到的平面结构拼接成多边形网格。简单地使用所有平面全相交的方法进行空间切割会导致大量的冗余切分结果,既降低了算法的整体效率,也极大地增加了内—外标记问题对应的搜索空间,造成最终重建模型难以保持紧凑的平面结构特征。如1.3节所述,有许多方法尝试减少空间分割的冗余程度,但这些方法难以平衡空间分割质量和计算效率。其中,降低冗余程度的关键在于,每个特征平面应该只分割它附近的空间,而不会造成全局性的影响。因此,采用层次化的空间分割策略,通过建立BSP树结构迭代地对空间进行二分割。实验结果表明,这种空间分割方法不仅具有非常高的效率,同时保证了分割结果的准确性。该方法使得处理由几百甚至上千个特征平面组成的物体成为可能,保证了重建模型更加完整并且包含更多的细节特征。
本文采用多边形对齐的二叉空间分割算法(polygon-aligned binary space partitioning)对3维空间进行切分。如图4所示,这是一种递归地将3维空间分割为凸多面体集合的方法,黑色边框表示模型的包围盒,其内部的线段表示每个凸包,通过层次化地分割空间,可以建立BSP树,树的每个叶子节点对应一个凸多面体。具体来说,本文将每个特征平面中的元素(点云或三角面片)投影到它的支撑平面上,并提取它的凸多边形作为空间分割中使用的几何结构。从初始的包围盒空间开始,每次挑选面积最大的凸多边形,用支撑平面将子空间一分为二,也将其他的多边形划分到相应的新子空间中。如果支撑平面与某个多边形相交,则将这个多边形一分为二,以确保子空间内的多边形不会超过子空间的范围。不断递归地分割子空间,直到不存在可分割的子空间为止。由此建立了BSP层次结构,BSP树的每个节点对应一个凸多面体,所有叶子节点组合成完整的包围盒。
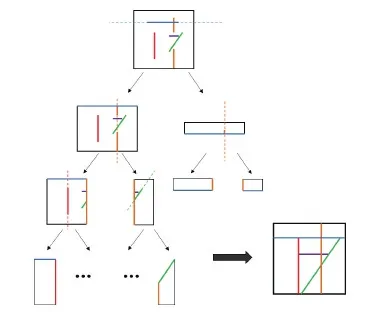
图4 BSP示意图Fig.4 Binary space partitioning
由图4可见,每个特征平面对空间分割的影响被限制在相应的子空间中。Chauve等人(2010)方法只考虑了两个层级,且第1层空间划分是轴对齐的(axis-aligned),与之不同的是,本文算法对空间进行多层级分割,且空间划分是基于多边形对齐的(polygon-aligned)。与Bauchet和Lafarge(2020)的动态增长方法不同之处在于,在每次空间分割的过程中,本文算法只需要考虑子空间内的多边形,不需要进行全局碰撞检测,从而降低了算法的计算复杂度。
事实上,BSP层级结构的思想也可以与动态增长的方法相结合,即每次挑选子空间内最大的K个多边形进行“扩张—碰撞—停止”将子空间分割,这样可以降低多层级分割中多边形先后顺序的影响。但本文采取了另一种更简单的方法,在空间分割之前,将多边形等比例放大α倍(默认α=0.3),这样可以提高算法对不完整的输入数据的鲁棒性。如果选择将所有多边形无限放大,多层级分割便退化为全相交分割,使得算法在效率和保真度之间可进行自由取舍。
算法2:BSP空间分割
待分割多面体集合S←∅
将包围盒加入S
所有多边形等比放大α倍 (不超过包围盒)
whileS≠∅ do
从S中取待分割多面体C
ifC中包含多边形 then
Pm←C中最大的多边形
(Ca,Cb)←用Pm的支撑平面分割C
将Ca和Cb加入S
forC中不与Pm共面的多边形Pido
ifPi与Pm的支撑平面相交 then
(Pa,Pb)←用Pm的支撑平面分割Pi
将Pa,Pb分别加入Ca,Cb
else
将Pi加入相应的Ca或Cb
2.4 表面提取
与Bauchet和Lafarge(2020)的方法类似,本文将表面提取问题定义为多面体的内外分类问题,通过提取所有内部多面体和外部多面体之间的分界面构成模型表面。对此,本文提出一种基于光线射击的马尔可夫能量方程,并使用最小割算法进行求解。
符号H表示多面体的集合,xi∈{in,out}表示每个多面体的二元分类标签,能量方程由式(4)所示,用于衡量整体分类结果X={xi|i∈H}的质量,即
E(X)=D(X)+λB(X)
(4)
正则项B(X)衡量了输出模型的表面积大小,用于控制模型的复杂度。惩罚表面积的方法往往会遗漏面积较大的薄结构,因此本文将面积权重加入正则项B(X)中,具体形式为
(5)
式中,AP为所有相邻多面体的集合,A为归一化因子表示所有多边形的面积之和,aij表示相邻多面体的公共多边形面积,wij表示该公共多边形与原始数据之间的重合度,作为该多边形权重。1{·}表示当括号内条件满足时返回1,否则返回0。
图5展示了wij的物理含义,即该多边形内部点构成的alpha-shape的面积与该多边形面积之比,其中五边形表示公共多边形,中间的不规则多边形表示多边形内部所有点构成的alpha-shape,两者面积之比度量了该多边形被原始数据的覆盖程度。覆盖率越大,则wij的值越大,对应的惩罚则越小,该多边形组成物体表面多边形的概率越大。
图5 点覆盖率示意图Fig.5 Point coverage diagram
数据项D(X)衡量了输出表面模型的保真度。本文使用一种基于光线射击的投票方案,确定每个多面体的内—外标签。由于多面体的大小不同,较大的多面体往往具有更大的表面积,会受到B(X)的更高惩罚。为了消除这种偏差,将体积权重加入数据项D(X)中,具体形式为
(6)
(7)
图6 基于光线射击的投票策略Fig.6 Voting strategy based on rays shooting
λ是控制输出多边形网格的复杂度和保真度的参数。图7展示了输出结果的复杂度和保真度与λ的关系。为了同时保证结果的复杂度和保真度,本文算法默认将λ设为0.2。

图7 参数λ的影响Fig.7 Impact of parameter λ
通常,马尔可夫场对应的二元标记问题可以转化为多面体邻接图G=(V,E)上的最小s-t切割问题。其中,V表示多面体集合,E表示相邻多面体集合。V增加了两个额外的节点:源点s和汇点t。这两个节点和所有多面体节点相连。能量方程E(X)定义了每条边上的权重。连接源点或汇点的边的权重会惩罚相关的多面体分区,而两个分区之间的边的权重会惩罚对应的公共面。至此,最小化能量方程问题就转化成了求图的最小割问题。通过Boykov和Kolmogorov(2004)提出的最大流算法求解出每个多面体对应的标签。最终,提取所有内—外区域分界面作为物体的表面多边形网格。
3 实验与分析
本文代码为C++语言编写,主要基于计算几何算法库CGAL(computational geometry algorithm library)进行实现。CGAL提供了本文所需的基本几何运算,以及最近邻搜索、主成分分析和2维三角剖分等稳健高效的算法。本文算法在CGAL内核上进行开发,考虑到浮点数运算的舍入误差,为了避免考虑复杂的边界条件和快速验证本文算法,在空间分割阶段中选择使用CGAL的有理数表示进行精确计算。
此外,使用3D组合图来表示分割结果。组合图是对被细分的对象的拓扑结构进行建模的一种以边为中心的数据结构,通过darts和darts之间的一组指针有效地表示了所有cells之间的入射关系和邻接关系,便于快速访问邻居,且易于修改(如,增加cells或删除cells等),并有效降低了时间复杂度,是半边数据结构到更高维度的推广。2D组合图等价于半边数据结构,其中halfedges对应于darts,将对象分解成顶点、边和面。3D组合图将3D对象分解为顶点(0-cells)、边(1-cells)、面(2-cells)和体(3-cells)。在空间分割环节中,空间包围盒被细分成多个分区,所以需要这样一个数据结构来表示对象的细分。在分割开始前,本文初始化一个由3D组合图表示的空间包围盒,每次分割等价于修改相应的cells以及darts之间的入射关系和邻接关系。分割结束后,组合图的2-cells对应于所有的内部面片和切割空间包围盒得到的面片,3-cells即为空间分割得到的凸多面体分区。
3.1 数据集
本文算法已应用在各类由点云和三角网格表示的真实世界物体上,相关的数据集包括:
1)从CAD模型中采样获得的点云,如Castle、Hilbert Cube等。采用的CAD模型均取自Thingi10K数据库。该数据完整、干净,正确的平面检测结果即可确保较为准确的重建模型。
2)从拥有自由表面的物体中采样获得的点云,如Stanford Bunny、Hand和Fertility等,这类物体的最终重建结果由紧凑的多边形网格近似表示。
3)由MVS(multi-view system)得到的稠密建筑物三角网格。这类数据往往具有较大的噪声,无法通过小平面形状来正确地捕获细节,对平面检测及拼接算法提出了更高的挑战。
4)通过激光雷达扫描产生的点云数据。这类数据在几何上更准确,但由于现实场景中普遍存在的遮挡现象,导致输入数据往往存在缺失部分数据和大量异构点等缺陷。
图8中展示了一些原始数据和相应的重建结果,其中每个模型的左侧为输入,右侧为输出。可以看出,本文算法具有较高的鲁棒性,可以处理多源且各式各样的真实世界物体,验证了该方法的适用性。此外,由于建筑数据往往底部数据缺失,本文在计算能量方程时忽略指向底部且未击中面片的射线。
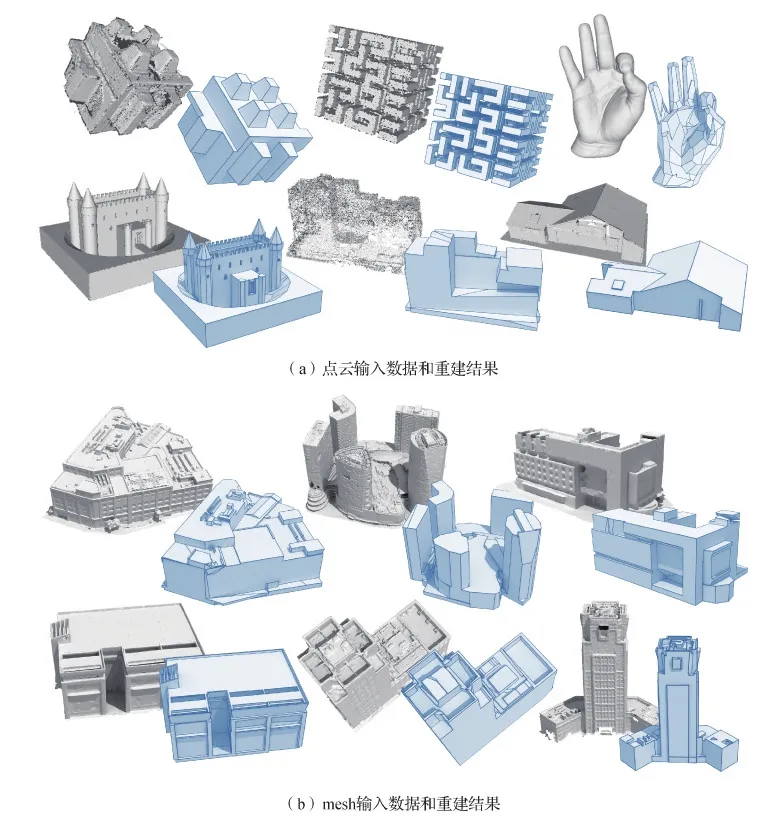
图8 输入数据和结构化重建结果Fig.8 Piece-wise planar reconstruction on different data((a) data of point cloud and results; (b) data of mesh and results)
3.2 衡量指标
本文从输出多边形网格模型的保真度、复杂度和算法的运行时间3个方面评估该算法。模型保真度通过计算输入数据和输出网格之间的均方根误差(root-mean-square error, RMSE)来衡量,输出结果的复杂度通过输出的面片数量来量化表示。
表1展示了本文算法在各类数据上的性能表现。BSP分割较为耗时,大约70%的计算工作都集中在分割事件的处理上。在可扩展性方面,本文算法可以在没有并行化方案的标准计算机上处理由上万个几何平面组成的物体。
3.3 与KSR对比
将本文算法与state-of-the-art结构化重建算法(kinetic shape reconstruction, KSR)进行定性、定量比较。与本文一样,KSR(Bauchet和Lafarge,2020)旨在降低空间分割的冗余程度。因此,为了建立公平的比较机制,对比实验对两种方法使用了相同的特征平面数量。
图9显示了两种方法将从同个模型上检测到的相同个数的特征平面拼接成结构化模型的对比结果,其中T、|F|、E分别表示分割时间、输出的表面模型面片数量和以包围盒对角线的百分比形式表示的RMSE。可以看到,相同平面下,本文算法耗费的时间更少、生成模型面片数更少、RMSE更小,同时保留了更多的细节特征。这是由于本文算法给定的能量方程加入了面积权重,使得算法对薄结构的保持更加鲁棒,提供了更好的保真度和复杂度之间的折中。然而由于现实数据往往存在噪声、遮挡等缺陷,且两者都受限于多个参数的影响,仅靠RMSE无法准确地评判两者的优劣。本文更加侧重该算法对时空复杂度上的贡献。

表1 本文算法在不同数据上的性能表现Table 1 Performance on different data of proposed method
图10比较了这些方法的可扩展性,与KSR相比,本文算法速度更快、冗余程度更低,相应地,可以使用更多的平面进行空间分割。KSR的全局碰撞检测限制了它的运行效率,局部性是本文效率提升的关键,随着特征平面数量的增加,本文算法运行时间较之KSR降低了至少两个数量级。
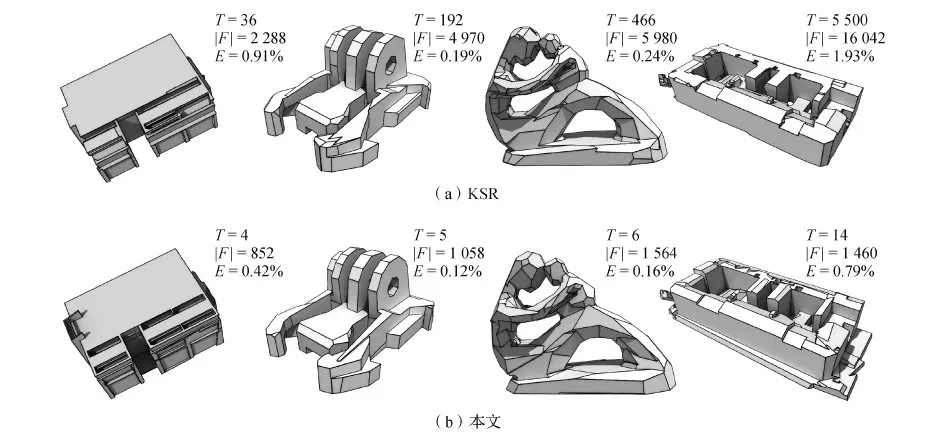
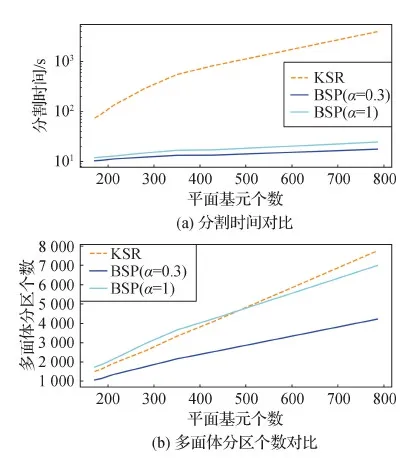
图10 KSR方法与本文方法的比较Fig.10 Comparison with KSR in space partition ((a) comparison of partition time; (b) comparison of polyhedron number)
3.4 消融实验
本文提出的结构化重建算法主要依赖于多源区域增长和二叉空间分割(BSP)这两个操作。为了评估这两个部分对算法整体性能和结果质量的影响,进行如下消融实验。
1)为了验证多源区域增长算法的有效性,本文对比了在相同输入数据的情况下,利用单源区域增长和多源区域增长算法进行平面检测分别对后续结构化重建结果造成的影响。如图11所示,单源区域增长的区域大小依赖于区域增长的先后顺序,而多源区域增长检测到的平面形状更均匀,且RMSE更小,特别是对于自由形式或包含曲面元素的对象,多源区域增长通过更加合理地划分区域的边界有助得到更准确的平面结构,重建结果误差更低,视觉效果更好。
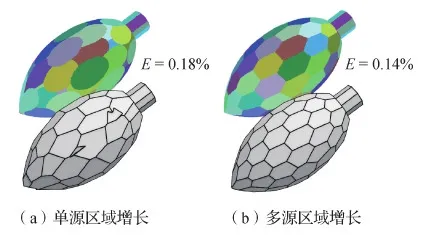
图11 多源区域增长的重要性Fig.11 Validation of multi-source region growing ((a) single-source region growing; (b) multi-source region growing)
2)为了验证BSP分割算法的有效性,对比了利用相同平面检测结果对3维空间分别进行相同平面形状个数下全相交分割和BSP分割对整体算法性能的影响。如图12所示,本文BSP分割算法降低了后续内—外标记问题的搜索空间,使得重建结果更轻量紧凑,更好地体现平面结构特征。同时,BSP分割算法使得计算时间降低了两个数量级,证明了该方法的快速性。而使用全相交分割,计算时间和多面体数量都会成百倍的增加。其中|H|表示分割得到的多面体分区个数。

图12 BSP分割的重要性Fig.12 Validation of BSP based partition ((a) 208 plane shape; (b) BSP based result; (c) exhaustive-partition based result)
3.5 与简化算法对比
为了表明本文算法对于保有物体的重要结构化特征和细节的有效性,将该算法分别与经典的网格简化方法QEM(quadric error metrics)、VSA(variational shape approximation)进行对比,对比结果如图13所示。
QEM(Garland和Heckbert,1997)通过边—坍塌操作减少网格面片至目标数量,无法正确捕获物体的结构;VSA(Cohen-Steiner等,2004)根据模型的平面结构简化模型,但会产生面片折叠的问题,图13(b)中红色面片表示其法向量朝向错误。这两种方法都无法修复输入模型本身的缺陷。
通过比较本文方法返回的多边形面片可以更有效地逼近几何对象。特别是对于结构化特征明显的真实世界中的人造物体(例如建筑的墙壁、屋顶等),本文算法可以有效保有其重要的几何结构,并生成轻量级的拓扑正确且具有现实意义的参数化模型。同时,该方法支持直接对点云数据进行相应处理,可以不依赖于稠密网格重建这一步骤,避免了其中可能发生的几何和拓扑错误。
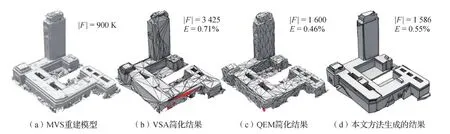
图13 简化算法对比实验Fig.13 Comparisons with surface approximation methods ((a) MVS mesh; (b) VSA result; (c) QEM result; (d) ours)
4 结 论
本文采用特征平面检测、空间分割和表面提取的流程结构化重建轻量级网格模型,在保留平面结构特征的前提下保证模型水密、无自相交,尤其适合于富含结构特征的物体模型。流程中的3个步骤相互解耦,多源区域增长算法可以改善光滑曲面上的特征平面检测效果,层次化的空间分割是降低搜索空间、提升整体流程效率的关键,并且在特征平面检测缺失的情况下可以通过放大多边形来提高鲁棒性。本文算法的局限性在于,重建质量依赖平面基元检测的结果,在基元检测时本文只考虑了单体模型数据,没有利用大量相似模型的统计信息,这限制了基元检测的质量。此外,本文算法只适用于重建物体的水密模型,当输入数据存在大面积缺损时(如建筑数据底部缺失),本文算法依赖于包围盒填补缺损部分。未来将基于数据驱动的方法改进几何结构检测效果,结合隐式场进一步改善空间分割的质量,并探索利用多层级空间分割进行LOD重建的方法。

