显微光学模糊图像的景物深度提取及应用

苗国超，魏阳杰，侯威翰

东北大学计算机科学与工程学院, 沈阳 110004

0 引 言

在生物医学、机器人微操作和材料科学等领域，微纳米尺度下的高精度观测是目标识别、特征检测和信息获取的必要条件和关键技术(Herath等，2014；Barretto等，2011)。目前，能够实现微纳米尺度观测的技术主要包括荧光显微技术、原子力显微技术、电子显微技术(Wetzer等，2019)和光学显微技术。

荧光显微镜可以通过入射激光激发出的荧光信号获取样品的纳米级图像，但荧光信号衰减快，无法实现连续成像且荧光剂易对样品(如活性细胞)造成损伤(Rodriguez等，2016)。原子力显微技术是通过探针逐点扫描样品表面成像，精度可以达到纳米尺度，但成像过程耗时，不适用于动态样品特性观测(Ghosh等，2016)。电子显微镜是根据电子光学原理，用电子束和电子透镜代替光束和光学透镜，实现物质的细微结构的纳米尺度成像，缺点是要求真空观测环境、不适合动态样品成像、样品有损制备且价格昂贵。与上述观测技术相比，光学显微成像技术具有对环境要求低、对样品无损和直观快速等优势，但是，高精度光学显微镜的放大倍数高、景深小，容易出现离焦成像模糊现象，即物距、像距和焦距之间不满足几何成像中的高斯成像公式时，点光源成像发生能量扩散现象。另外，传统的光学显微镜一般只能得到景物2维图像，缺少景物3维形貌信息。因此，如何从光学成像过程的能量分布和能量传播特性出发，探索图像模糊程度定量评价标准，建立图像的模糊程度、景物深度以及系统参数之间的关系模型是提升光学图像成像分辨率、恢复景物深度信息的关键，也一直是光学领域的研究热点。

Pentland(1987)最早提出了离焦深度重建方法(depth from defocus，DFD)，利用光学离焦模糊图像的模糊程度求解景物深度。此后，很多学者对如何建立图像的模糊程度和景物深度之间的关系进行了一系列研究。根据几何光学，可将离焦模糊图像的能量分布模型抽象为一个圆盘点扩散函数，然后通过建立点扩散函数的扩散半径与深度的关系来恢复景物深度。Subbarao和Gurumoorthy(1988)考虑透镜的非理想性以及其他因素，用2维高斯函数替代圆盘函数作为点扩散函数，建立高斯函数的标准差与景物深度之间的关系。在很多应用中，高斯函数相对于圆盘函数能够更加准确地描述点光源能量扩散特性，但是，标准差和扩散半径的关系与系统参数紧密相关。因此，在测量景物模糊图像的模糊程度之前，需要进行一系列的标定实验得到这个关系参数，标定过程烦琐、耗时(Subbarao，1989)。更重要的是，无论是圆盘函数还是高斯函数，都需要根据模糊图像测量点扩散函数的半径值来衡量图像的模糊程度。然而根据模糊原理，一幅模糊图像是很多个点光源模糊成像的叠加。因此，根据图像特性直接测量点扩散函数半径值是非常困难的，实际中往往需要引入优化迭代方法才能逼近真实的半径值(张颖 等，2014；刘克 等，1994)。

为了直接表征光学图像的模糊程度，也有学者引入Laplace、Sobel和Canny等边缘检测算子来测量图像中边缘亮度的变化速度，进而描述图像模糊程度的变化情况 (代文征和杨勇，2019； Wei等，2018；Xie和Tu，2017；郑莹和孙燮华，2005)。这种模糊测量方法是许多光学相机自动聚焦的本质。但是因为与系统参数和景物深度都没有直接的数学关系，无法根据这些算子准确建立图像的模糊程度与光学系统参数、景物深度之间的数学关系模型。另外，这些模糊程度的评价值与景物纹理、亮度等图像特征紧密相关，鲁棒性差。更重要的是，显微成像系统中，光的衍射、折射现象影响显著(Sheinin等，2020；Scandolo等，2018；Jeon等，2019)，光学系统参数对成像质量的影响是复杂且相互耦合的，这些评价方法多是单纯依据图像特性实现模糊评估的，不考虑光学系统参数，很难准确反映系统的整体特性。

曾明等人(2004)提出利用图像的高频能量参数表征光学图像的模糊程度，并使用不同深度的序列模糊图像标定出图像高频能量参数与深度之间的关系模型。实际中，测得一幅模糊图像的高频能量参数后，可以根据标定的关系模型获取深度信息。尽管提取模糊图像高频能量参数的过程非常直接方便，但是因为关系模型不具有通用性，测量不同的样品深度前，都需要重新进行标定实验，过程烦琐、耗时。孙明竹等人(2009)提出通过显微物镜离焦光学传递函数建立景物深度和图像模糊程度的关系实现深度测量。此方法中图像模糊程度是用传递函数中的光程差参数表征的，而从模糊图像中无法直接求解出光程差。因此，必须通过清晰图像和模糊图像的逐个像素亮度值比较，根据最小二乘方法搜索两幅图像的亮度差最小时即可得到模糊图像的深度信息。但是，求解的每幅模糊图像的深度都需要进行逐点比较和搜索，这个过程需要大量运算，测量精度低。梁锐等人(2020)提出了一种基于模糊图像和B样条小波变换的自适应距离测量方法，虽然比传统基于高斯模糊图像的距离测量方法精度更高，但是此方法的测量误差为米级别，而对于显微光学图像要求微纳米级别的误差，显然是不适应的。

综上所述，现有根据图像的模糊程度求景物深度的方法存在以下问题：1)尽管可以建立点扩散函数的半径与景物深度之间的函数关系，但是直接测量一幅模糊图像的点扩散半径非常困难，常见的迭代求解方法时间长；2)使用边缘检测算子表示图像模糊程度时，因为缺少图像模糊程度与光学系统参数、景物深度之间的准确数学关系，深度计算的鲁棒性差；3)使用高频能量参数表征光学图像的模糊程度的方法，需要标定实验或者图像亮度比较求解深度，计算量大、精度低。

为了解决上述问题，进而更好地对模糊图像进行景物深度还原和清晰重构，本文结合高频能量参数和系统光程差参数，基于显微光学系统中的光学传递特性，建立高频能量参数与景物深度之间的函数关系，并通过归一化和曲线拟合的方法得到显微光学系统的成像模糊程度与景物深度之间的解析函数，最后基于解析函数对模糊图像进行景物深度还原和清晰图像重构。实验验证了本文提出的模糊程度与景物深度之间函数关系的有效性、准确性和不同景物间的通用性。本文方法的创新性主要体现在3个方面：1)提出的模糊程度与景物深度之间的函数关系充分考虑到实际光学成像中多透镜集成成像以及复杂的系统参数，相比简单的凸透镜成像模型，能够更加直观地反映系统参数对光学模糊成像过程的影响；2)采用高频能量参数表征图像的模糊程度，建立与景物深度直接的函数关系，不需任何标定和迭代过程；3)固定光学系统参数后，建立的归一化系统成像程度与景物深度之间的解析函数不会受到景物图像的纹理、亮度等特性差异的影响，适用于不同的样品，鲁棒性强、更方便、更省时。

1 光学系统中的光学传递特性

1.1 显微物镜的光学传递函数

光学显微系统中，聚焦和离焦成像时波前球面对比示意图如图1所示。其中，S为聚焦点O对应的参考球面；S1为离焦点P对应的近离焦波前球面；点A为极限光线在球面S1处的入射点；w为离焦成像时的波前球面与参考球面在极限光线处的光程差；I0为清晰成像时的系统像距，I为像距相对于理想像距的变化值；α′为物镜像方孔径角。

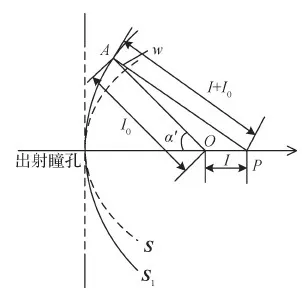
图1 聚焦和离焦成像时波前球面对比Fig.1 Comparison of wavefront spherical surface in focus and defocus imaging

Hopkins(1955)最先推导出显微镜的光学传递函数(optical transfer function，OTF)的形式，描述了光程差与光学传递特性之间的关系，具体为

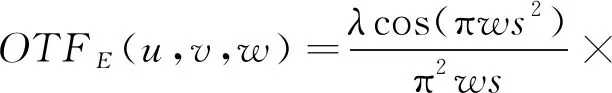
(1)

式中，Jn(·)表示n阶贝塞尔函数；λ为显微镜系统的中心波长；s是归一化的空间频率；(u,v)表示像平面的空间频率。

由于式(1)计算非常复杂，Stokseth(1969)通过简化得到了OTF的近似表达式，具体为

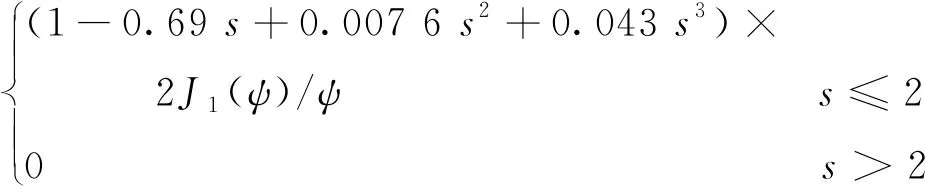
(2)

空间频率s与像平面的空间频率(u,v)的关系为

(3)

式中，fc为光学系统截止频率。

对图1标识的三角形AOP应用余弦定理，可以得到光程差w与像距变化I的关系，即

(4)

为了得到像距变化与物距变化之间的关系，引入几何光学成像中的高斯公式，具体为

(5)

式中，d0是光学系统的理想物距；d是物距相对于理想物距的变化值。

根据式(5)，像距变化I与物距变化d的关系可以转化为

(6)

将式(6)代入式(4)，传递函数参数光程差w与物距变化d的关系转化为

(7)

孙明竹等人(2009)利用式(7)物距变化与光程差的关系实现深度测量，基本原理是使用光学传递函数的光程差参数表示图像的模糊程度，并建立模糊度与深度的关系模型。由于从图像中不能求取光程差，该方法通过清晰图像和模糊图像的逐个像素点比较和搜索得到模糊图像的深度信息。但是，逐点比较和搜索过程运算时间长、计算效率低。

在上述研究的基础上，本文继续探索物距变化与光程差之间的关系，以及物距变化对光学系统成像特性的影响。首先，固定焦距、孔径角等系统参数，观察d和w之间的关系曲线如图2所示。从图2可以看出，光程差w和d以d=0为中心近似呈对称的线性关系；当景物与相机的距离等于理想物距时，物距变化为零，此时光程差非常接近于零。当物距变化变大时，光程差增大，那么根据式(2)可知系统的传递函数OTF必然会随之发生变化，进而改变光学系统的成像特性。

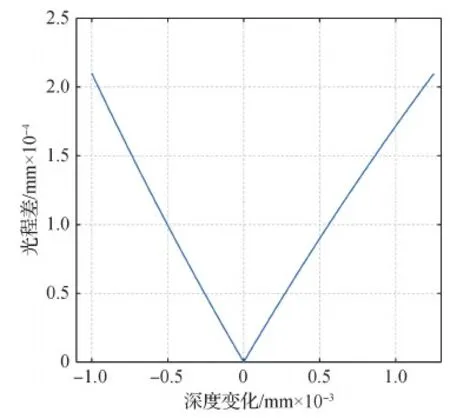
图2 物距变化d与光程差w的关系Fig.2 Relationship between distance variation d and optical path difference w

1.2 光学模糊成像模型

对于线性不变系统，空间域内一幅模糊图像可以表示为(Pronina等，2020；郑楚君 等，2004)

g=g0*h+n

(8)

式中，g为模糊图像；g0为清晰图像；h为成像系统的点扩散函数，也称退化模型；n为加性噪声；*为卷积运算。

根据几何光学理论，当景物深度相对于理想物距发生变化时，点光源模糊成像的圆斑半径rg可以表示为

(9)

式中，D表示摄像机的有效半径。

传统的模糊深度模型多使用高斯函数近似点扩散函数h，假设高斯函数的标准差σ和模糊圆斑的半径之间的参数为γ，那么，代入式(9)，高斯标准差为

(10)

从式(10)可见，固定系统参数后，σ是景物深度变化d的函数。一般σ用来表示图像的模糊程度，即d越大，σ越大，图像越模糊。但是，如果d未知，则很难根据一幅模糊图像计算σ。

在频率域中，类似地，可以得到景物深度变化与图像模糊程度之间的关系。首先，频域内的点扩散函数H也称为OTF，那么，式(8)对应的频域表达为

G(u,v)=G0(u,v)H(u,v)+N(u,v)=
G0(u,v)OTF(u,v,w)+N(u,v)

(11)

式中，G和G0分别为频域内的模糊图像和清晰图像，N为频域内的加性噪声。

如式(2)所示，固定系统其他参数时，OTF是光程差w的函数。为了分析w的大小对光学传递特性的影响，分别取w等于λ、λ/2、λ/3、λ/4，计算对应的OTF响应曲线，结果如图3所示，空间频率s的单位为线对/毫米(lp/mm)。从图3可以看出，OTF响应曲线随光程差的增大而逐渐衰减，离焦的OTF对高频信号起抑制作用。根据光学成像的构成特性，低频信号决定图像轮廓，高频信号决定图像细节，图像高频信号的丢失意味着图像的模糊。因此，w越大，图像的高频信号越少，图像越模糊。但是，与时域内的点扩散函数半径或者高斯函数的标准差相似，实际应用中，很难测量出一幅模糊图像的w值。因此，引入高频能量参数描述图像的模糊程度，建立显微光学系统成像模糊程度与景物深度之间的解析函数。

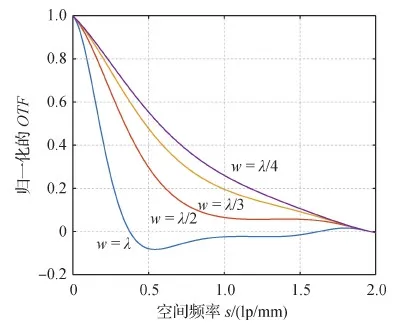
图3 不同大小的w对光学传递特性的影响Fig.3 Influence on transfer property of different w

2 模糊程度与景物深度之间解析函数

2.1 模糊图像中的高频能量

根据图3可知，模糊图像中的高频能量参数越少，图像越模糊。图像处理中一般可以使用频域内的高通滤波器滤除一幅模糊图像G1中的低频分量，保留高频分量。处理后，图像剩余的高频部分G′1为

G′1(u,v)=G1(u,v)×GHP(u,v)=
OTF(u,v,w)×G0(u,v)×GHP(u,v)

(12)

式中，GHP(u,v)表示高斯高通滤波器，即

(13)

式中，D0为高通滤波器截止频率，一般取为4(曾明 等，2004)；M和N分别表示图像块的长度和宽度。

因为计算模糊图像的高频能量参量一般在空间域进行，所以需要将G′1转换到空间域，即

(14)

模糊图像g1的高频能量参数定义为

(15)

由式(15)可知，每一幅模糊图像都可以得到一个对应的Eh值，如果固定光学系统参数，改变景物深度d以得到一系列不同深度条件下的模糊图像g1(x,y,d)，那么就可以获得代表图像模糊程度的Eh与景物深度变化d之间的函数T，具体为

Eh=T(d)

(16)

为了得到函数T的解析式，同时为了避免不同纹理、亮度的景物图像对T的影响，将序列图像的Ehi值进行归一化处理，即

Ehi_norm=Ehi/Eh0

(17)

式中，Eh0为图像序列中最清晰图像的高频能量参数。

通过曲线拟合方法可获得该光学系统的高频能量参数Ehnorm和深度变化d之间的函数，具体为

(18)

(19)

(20)

2.2 基于光学传递函数的清晰图像重构

基于式(18)中的模糊程度与景物深度之间的函数关系，当获取一幅景物的模糊图像后，可以求解出该图像的深度d，再根据式(7)计算光学传递函数OTF中的参数w，得到光学传递函数后，就可以重构频域内景物的清晰图像，即

(21)

实际应用中，OTF(u,v,w)可能出现零值或者在高频时其值会很小，为了处理这种情况，可为其增加一个常数值，即

(22)

式中，C(u,v)是一个非常小的常数，本文设置为0.000 1。

最后，将F(u,v)通过傅里叶逆变换到空间域，即得到空间域内的清晰图像。

本文提出的显微光学系统成像模糊程度与景物深度关系曲线的获取方法的具体步骤如下：

1)初始参数设置。包括图像块大小M和N、序列图像步长、滤波器截止频率D0、清晰图像g0、显微镜系统中心波长λ、显微镜像距I0和焦距f。

2)使用式(15)计算不同深度序列图像的Eh值。

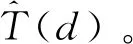
1)输入一幅待测景物的清晰图像，通过式(15)计算清晰图像的Eh0N。

2)将清晰图像的Eh0N代入到式(20)。

3)输入该景物的任意一幅模糊图像块j，通过式(15)计算其Ehj。

4)将Ehj值输入式(20)，求解模糊图像块j的深度值d。

5)使用式(7)计算w，并根据式(2)得到OTF。

6)根据式(22)得到清晰频域图像，使用反傅里叶变换得到空间域清晰图像。

7)拼接图像块，得到景物完整的清晰图像。

2.3 模糊程度与景物深度之间的关系曲线验证

为了验证深度变化d与高频能量参数Eh的关系，使用自主研发的实验显微成像平台采集标准纳米栅格图像，实验平台如图4所示。

图4 实验平台Fig.4 Experimental platform

栅格是MikroMasch公司生产的TGXYZ系列正方形栅格，每个栅格的高度和宽度都为500 nm。

实验时，首先在被观测栅格处于显微镜的理想物距处时，采集栅格图像，如图5所示。然后，以理想物距处为起点，分别沿着镜头的光轴向远离镜头和靠近镜头的方向移动平台，移动步长为1 μm，得到一系列栅格的模糊图像。为了方便计算，将图像进行了切块，设置的图像块大小为140×140像素，截取后的图像块序列如图6所示。

图5 清晰栅格图像Fig.5 Focused image of grid

图6 截取后的部分图像序列Fig.6 Sequential images after cutting

首先验证本文模糊图像高频能量提取方法的正确性。由于采集图像序列时精准控制平台的移动步长，即每一幅模糊图像的深度变化值已知。因此使用图6中的清晰图像，根据式(16)计算图像序列的高频能量Eh作为真实的高频能量值。然后使用式(15)同样计算图6中序列图像的高频能量Eh，两次结果对比如图7所示。从图7可以看出，本文方法测得的高频能量值和真实高频能量变化规律完全一致，对相同图像的高频能量值非常接近，表明使用式(16)计算一幅模糊图像的Eh值是可行的。

为了进一步证明真实值和测量值两组数据是否具有一致性，采用相关系数法进行分析(汤淑春和文传源，1998)，以此验证本文计算Eh的方法。分析公式可以表示为

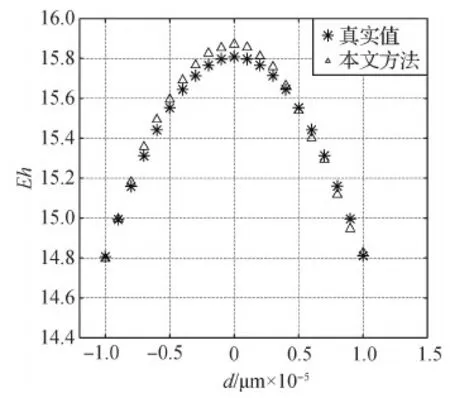
图7 本文方法计算的高频能量和真实值的对比Fig.7 Comparison between the high frequency energy calculated by our method and the ground truth

(23)

式中，Z12为两组数据的协方差；Z1为序列图像真实Eh数据的标准差；Z2为本文方法计算的Eh数据的标准差。

根据式(23)，计算求得R=0.992 4；一般来说，R> 0.95表示数据间具有很好的相关性，因此，证明本文使用高频能量值代表图像的模糊程度，建立的模糊程度与景物深度之间的函数关系是正确的。

然后，为了得到Eh和d之间的解析函数，首先将深度序列图像的Eh值归一化，再进行四阶曲线拟合，拟合结果如图8所示。拟合用四阶曲线表达式为

(24)

归一化的函数关系拟合参数为ɑ = 1.59×1017,b= 1.15×1012,p=-6.47×1010,q= 0.726,r= 1.00。曲线拟合的残差模值为0.005 3，表示四阶拟合误差很小。

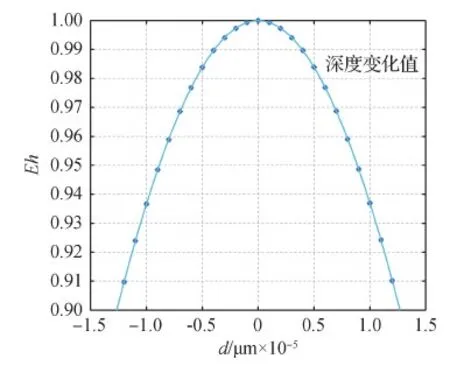
图8 模糊程度与景物深度间的拟合曲线Fig.8 Fitting curve between blur degree and scene depth

为了说明本文归一化的模糊程度与景物深度之间的函数关系的通用性，同样以1 μm为步长分别采集了条纹栅格和圆形栅格的序列图像进行建模实验，条纹栅格不同深度图像序列如图9(a)所示，圆形栅格不同深度图像序列如图9(b)所示。根据本文方法建立的两种栅格的模糊程度与景物深度关系曲线如图10所示。从图10可见，3种样品的模糊程度和深度变化之间的曲线几乎是完全重合的，证明本文建立的模糊程度与景物深度之间的函数关系归一化后，与景物的纹理和亮度特征无关，只与系统的特性有关。因此，实际应用中，对于不同的观测样品，不需要重新建立它们的模糊程度与景物深度之间的函数关系，只需要采集一幅新景物的清晰图像实现高频能量归一化处理，就可以使用已建的显微光学系统成像模糊程度与景物深度之间的函数关系计算模糊图像深度，重构该景物清晰图像。

图9 两种不同样品不同深度图像序列Fig.9 Different depth image sequences of two different samples ((a)images of stripe grid;(b)images of circular grid)

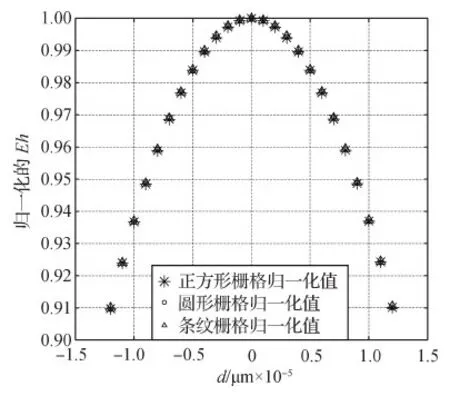
图10 3种样品的归一化模糊程度与景物深度间的曲线Fig.10 The curve between the normalized blur degree of the three samples and the depth of the scene

3 实 验

3.1 深度计算实验

首先，根据式(15)对图6中的序列图像求出高频能量Eh值，然后进行归一化处理，根据式(24)求解出序列图像的深度，结果如图11所示。可以看出，本文方法得到的实验深度值与真实深度值非常接近，误差最大值为0.117 μm，最小值仅为0.006 μm，而逐点比较搜索得到的深度值与真实深度值相差明显。

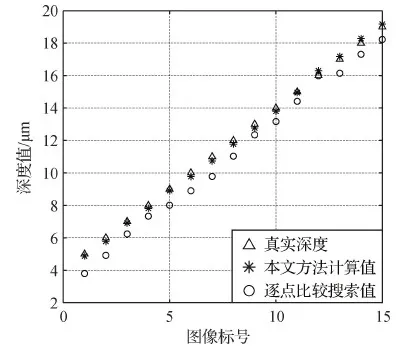
图11 模糊图像系列的真实深度和计算深度对比Fig.11 Comparison of the calculated height and the ground truth with the blurred image sequence

同时，为了更加清晰地表达本文深度计算方法的精度，通过计算相邻两幅图像的深度变化值来分析深度计算误差，平台的精确步长为1 μm，相邻两幅图像的深度变化值如表1所示，误差分析结果如图12所示。可以看出，本文实验测得的步进深度平均误差为0.008 μm，即相对误差为0.8%；逐点比较搜索法测得的步进深度平均误差为0.03 μm，即相对误差为3.0%。因此，与逐点比较搜索的方法相比，本文提出的显微光学系统成像模糊程度与景物深度之间的函数关系在深度求解时更为精确。

3.2 清晰图像重构

根据已知深度值进行模糊图像的清晰重构实验。选取一幅模糊图像，如图13所示，可以看出该样品并不是完全垂直于光轴，而是倾斜放置，自上向下倾斜，因此，图像各部分模糊程度是不同的。

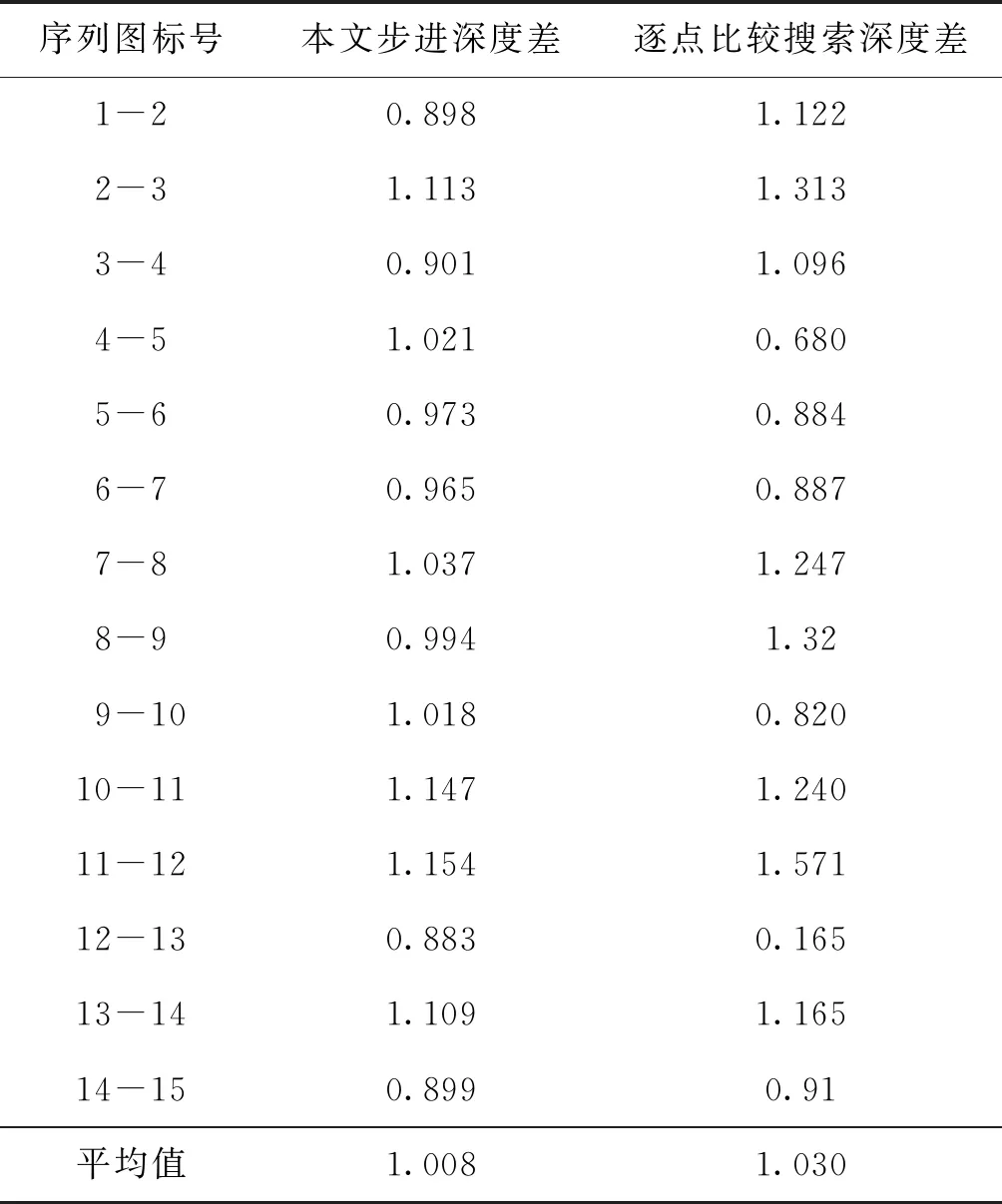
表1 相邻两幅图像的深度变化值Table 1 The depth change of two adjacent images /μm

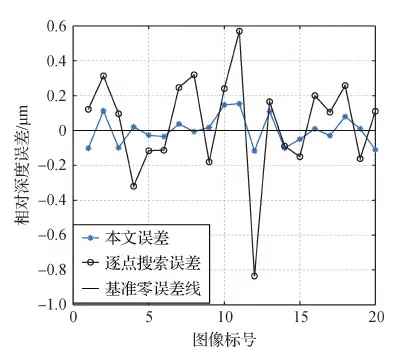
图12 相邻两幅图像的深度变化值误差Fig.12 The depth variation error of two adjacent images

图13 模糊图像Fig.13 Defocused original image

将图13切分为一系列大小一样的图像块，设置大小为140×140像素，相邻两幅图像块的重叠部分为70像素。清晰重构结果如图14所示。为进一步探究本文算法精度，对同一幅原图利用高斯模型反卷积方法进行实验比较，并从不同的图像清晰度评价标准进行对比。根据高斯分布的西格玛准则，数值分布在μ(平均值)两侧等于3σ(标准差)的距离范围内占总分布的99.7%。因此，本文中高斯标准差σ和模糊圆斑的半径rg之间的参数γ= 3。已知γ后，使用式(10)计算不同深度变化时高斯点扩散函数的标准差，然后使用高斯反卷积方法重构相同深度时的清晰图像，构建结果如图14(c)所示。

图14 模糊图像的清晰重构结果Fig.14 The reconstructed result of the defocused image ((a)original image;(b)reconstructed image using our method;(c)reconstructed image using Gaussian deconvolution)

对比图14(b)(c)可以发现，高斯反卷积方法得到的清晰图像在边缘处明显仍很模糊，而本文方法重建的景物图像能够很好地再现栅格边缘。为了量化对比两种方法，使用平均梯度值和拉普拉斯值对重构后图像的清晰度进行客观评价和分析，评价结果如表2所示。可以看出，本文方法重构后图像的平均梯度增加0.024 7，拉普拉斯值增加11.100 6，高斯反卷积方法重建图像的平均梯度增加0.020 5，拉普拉斯值增加9.001。可见使用本文方法重构的图像相比高斯反卷积方法，平均梯度和拉普拉斯值都明显更高。

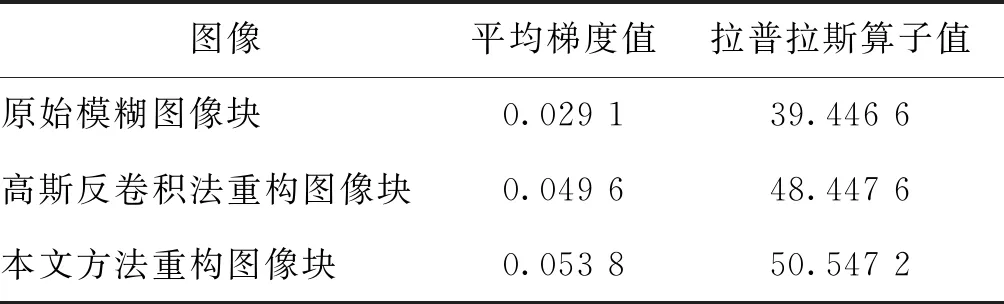
表2 重构后图像的清晰程度评价Table 2 Clarity evaluation of reconstructed images

然后，对不同深度变化时的序列模糊图像块进行清晰重构，图15(a)(b)分别为使用平均梯度值和拉普拉斯值对重构图像进行评价的结果。从图15可见，重构前的拉普拉斯平均值为37.5，平均梯度平均值为0.040 2，重构后的拉普拉斯平均为50.1，平均梯度平均值为0.056 3。可见，重构后图像的平均梯度和拉普拉斯值都有明显增加。另外，使用本文方法重构的不同深度值的模糊图像，平均梯度值在0.055 0.06之间，拉普拉斯值在50 50.2之间，表示重构后的图像块的模糊程度基本一致，也证明了本文方法对深度变化的序列模糊图像清晰重构的有效性和稳定性。

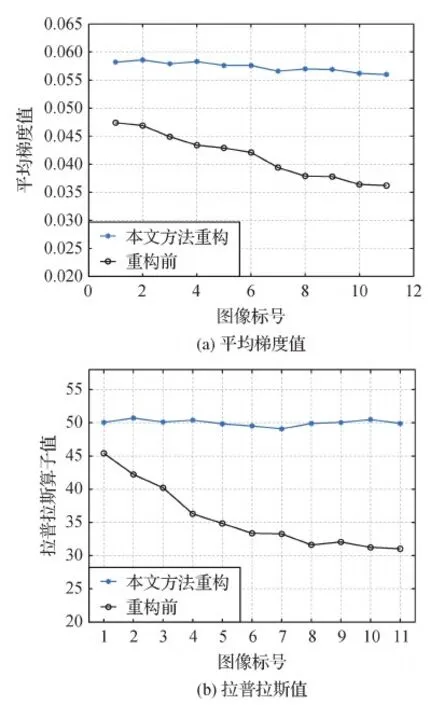
图15 不同模糊度图像块重构结果Fig.15 Reconstruction results of image blocks with different blur degrees((a)average gradient values;(b)Laplace values)

最后，将重构后的图像块按照切分顺序拼接为一幅完整图像，得到图13的整体重构结果，如图16所示。在图16中，随机选取18个区域求其平均梯度值和拉普拉斯值，并在原图13中找到对应区域，用高斯反卷积重构后，求其平均梯度值和拉普拉斯值。图17为两者结果对比图。可以看出，本文方法重构后图像的平均梯度值和拉普拉斯值都要高于高斯反卷积方法重构后的图像，且值非常稳定。说明本文方法可以用于大幅图像的清晰重构，且重构后图像的清晰程度基本一致。

图16 重构后图像块拼为完整图像Fig.16 The complete image after reconstruction and mosaic

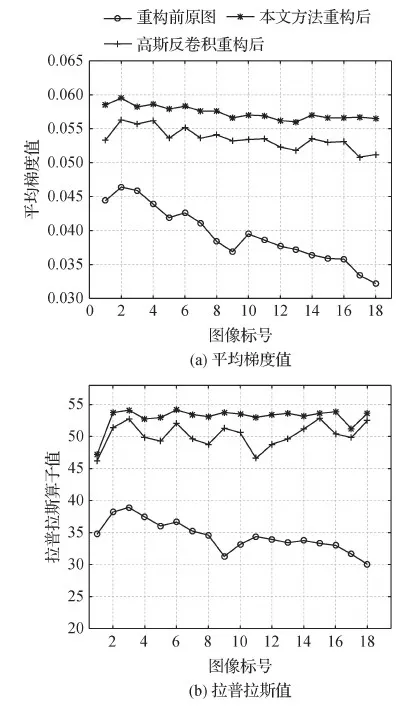
图17 本文方法和高斯反卷积法重构图像的清晰度对比Fig.17 Comparison of clarity values on the images reconstructed by our method and Gaussian deconvolution method ((a)average gradient values;(b)Laplace values)

3.3 通用性验证

为了验证本文提出的图像模糊程度与景物深度之间的函数关系曲线仅与具体的光学系统参数有关，而与系统观测景物的纹理和亮度等无关，即本文方法具有通用性，通过显微成像平台以步长为1 μm调节景物深度，得到条纹、圆形和凹陷正方形栅格的一系列模糊图像，如图18所示。根据本文算法，已经使用图6中的栅格图像建立了显微光学系统的归一化成像模糊程度与景物深度之间的解析函数，之后可以求解出序列模糊图像的深度值，求得的条纹、圆形和凹陷正方形栅格的深度结果如图19所示，对应的误差分析结果如图20所示。

图18 样品栅格的模糊图像Fig.18 The defocused images of the sample grids ((a)stripe grid;(b)circular grid;(c)concave square grid)

本文方法求解的条纹样品、圆形样品和凹陷正方形栅格相邻深度的平均误差分别为0.011 μm、0.015 μm和0.009 4 μm，逐点比较搜索方法求解的条纹样品、圆形样品和凹陷正方形栅格相邻深度的平均误差分别为0.039 μm、0.018 μm和0.021 μm。因为采集系列图像时相邻深度是固定的1 μm，因此，本文方法计算的条纹样品、圆形样品和凹陷正方形栅格相邻深度的相对误差为1.1%、1.5%和0.94%。逐点比较搜索方法计算的条纹样品、圆形样品和凹陷正方形栅格相邻深度的相对误差为3.9%、1.8%和2.1%。可见，利用本文归一化的成像模糊程度与景物深度之间的解析函数求解的这3种样品的深度误差都低于逐点比较搜索方法，这既说明了本文深度计算方法的准确性，更是表明本文的归一化成像模糊程度与景物深度之间的解析函数只与光学系统参数有关，与样品表面纹理和亮度等特征无关。

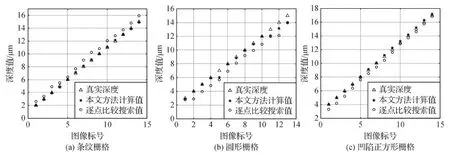
图19 不同栅格图像序列的真实深度和计算深度对比Fig.19 Comparison of the depth calculated by our method and the ground truth with sequential images of different grids ((a)stripe grid;(b)circular grid;(c)concave square grid)

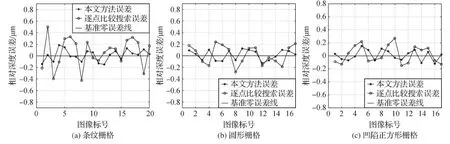
图20 相邻两幅图像的计算深度误差值Fig.20 The error of calculated depth of adjacent images((a)stripe grid;(b)circular grid;(c)concave square grid)

4 结 论

本文主要研究了显微光学成像中模糊图像的模糊程度与景物深度之间的关系和应用，包括以下3个方面：1)显微光学成像系统中的光学传递特性；2)表征图像模糊程度的高频能量参数与景物深度之间的函数关系获取；3)基于实际样品模糊图像的深度恢复与清晰重构。

首先分析了光程差的变化对光学传递函数响应的影响，推导出光程差与深度变化的关系，提取出图像的高频能量参数。然后建立高频能量参数与景物深度变化之间的关系曲线，并通过实验验证了此关系曲线的正确性。随后为了使本文方法对不同的景物具有通用性，对图像进行归一化处理，得到归一化的光学系统的成像模糊程度与景物深度之间的解析函数，以此函数关系为基础对图像进行了不同景物的深度恢复和清晰重构。最后使用本文方法与传统方法进行了对比实验，在图像深度恢复方面，本文方法比传统方法精度提高了约73%，在图像清晰重构效果上，本文方法清晰重构的图像的平均梯度值比传统方法提高8.4%，此拉普拉斯值计算值提高4.3%。

但是本文方法仍存在以下不足之处，本文研究主要针对静态景物，对动态景物进行观测时的有效性仍不明显，所以接下来开展的工作是动态景物的深度恢复与清晰重构，另外，当样品的尺度和平台位移可以比拟时，模型的适应性仍有待提高，这也是今后的研究方向。