不同立面收缩形式圆角弧边三角形超高层建筑的气动力特性
丁 通, 陈水福
(浙江大学 建筑工程学院,杭州 310058)
随着建筑高度的增长,超高层建筑的风荷载及风致响应问题日渐突出,并逐渐成为影响建筑安全性和舒适性的关键因素。为减缓过大的气动荷载及其响应,研究者们提出了不同的优化措施,其中改变超高层建筑沿高度方向的尺寸或形状,已被证实是一种效果显著的气动优化措施。顾明等[1-2]从气动措施和辅助阻尼器措施两方面综述了降低超高层建筑风荷载和风致响应的研究现状。Kim等[3-5]的研究显示,锥度化和退台均可减小建筑顶部均方根位移,但会增大个别风向角下的顶部加速度响应;这两种措施均可降低平均阻力系数和脉动升力系数,而退台对减缓脉动升力系数效果更佳;锥度化和退台还会影响风压功率谱带宽和峰值频率。对于方形截面高层建筑,锥度化可以有效消减作用于表面的风荷载,并抑制漩涡脱落强度[6-8]。Tanaka等[9]采取锥度化、退台和立面旋转等多种措施对多种类型截面的超高层建筑进行了风洞试验,结果显示,各种措施对不同气动特性的优化效果各不相同,建议对于特定的减小目标,应选取针对性的措施。邓挺等[10]研究了不同退台方式对方形截面高层建筑横风向风效应的影响,认为立面退台可以有效减小建筑横风向风效应,而退台旋转可以更大程度减小建筑的横风向荷载。Kumar等[11-12]通过风洞试验研究了正三角形截面高层建筑气动外形优化措施,发现立面旋转可以有效改善建筑表面风压分布以及三分力系数。Daemei等[13]针对正三角形截面高层建筑,采用数值模拟方法比较了锥度化、退台、立面旋转以及圆角、倒角、凹角等角部处理对阻力系数的影响,发现圆角处理能够最大程度减小阻力系数,最大降幅达到66%。
目前关于超高层建筑气动立面优化的研究主要集中于方形截面建筑,仅有少量针对正三角形截面建筑。事实上,从使用功能上看,正三角形平面的空间利用率不佳,故实际超高层建筑更多选择圆角三角形或圆角弧边三角形截面,如广州国际金融中心、上海中心大厦以及济南绿地中心等均选用此类截面,如图1所示。国内已有部分学者[14-17]对基于实际工程项目的圆角弧边三角形截面双塔高层建筑的干扰效应进行了研究,发现该效应主要体现在受扰建筑顶部峰值加速度明显增大。在此基础上,本文进一步对圆角弧边三角形超高层建筑采取气动立面优化措施,系统研究了两种地貌下锥度化、同向退台以及两种退台旋转对建筑三分力系数、基底横风向弯矩系数功率谱以及层脉动升力系数功率谱的影响,以期为同类超高层建筑的抗风设计提供理论依据。

图1 圆角弧边三角形超高层建筑Fig.1 Rounded corner arc triangular super high-rise buildings
1 风洞试验简介
试验在浙江大学ZD-1大气边界层风洞中进行。在试验地貌的选择上,Kwon等[18]和潘忠岳[19]各自通过对比多国最新风荷载规范,发现在定义基本风速的郊区地貌,如中国B类地貌或日本Ⅱ类地貌之中,相比之下中国规范的湍流强度偏小,有待进一步完善。鉴于此,同时也为了便于与现有文献结果进行对比,本次风洞试验的边界层风场模拟了两种日本地貌:郊区环境下的Ⅱ类地貌(风速剖面指数α=0.15)和城市环境下的Ⅳ类地貌(α=0.27)。风洞中的实测风速剖面和湍流度剖面,如图2所示。
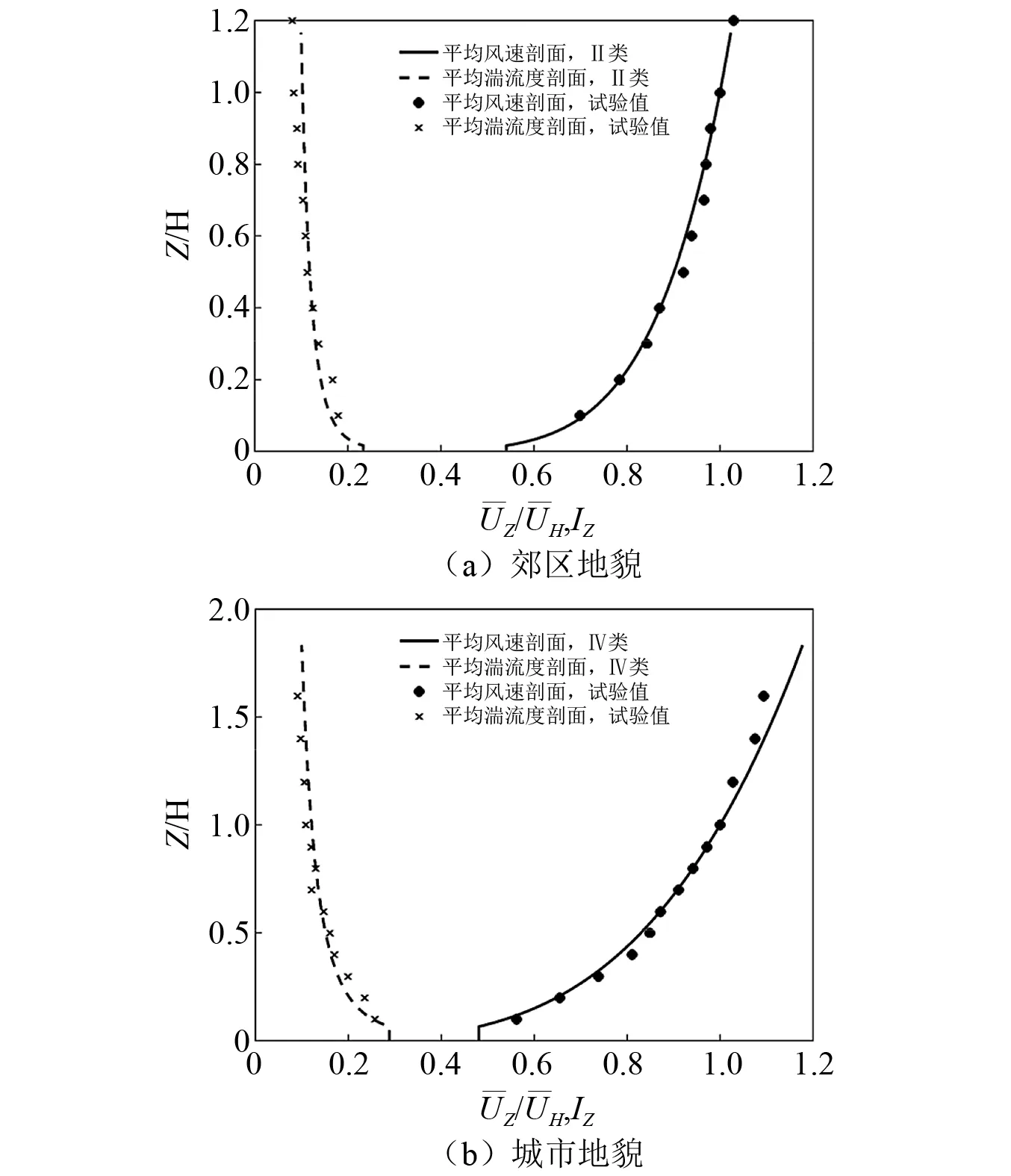
图2 风剖面模拟Fig.2 Simulation of wind-field profile
试验模拟的圆角弧边三角形超高层建筑原型底面边长60 m,高度300 m,试验缩尺比1∶300。试验模型包括:等截面的对照模型A;锥度(底面与顶部边长差与高度的比值)6.3%的低锥度模型B;锥度10.6%的高锥度模型C;两阶同向退台模型D;两阶退台底部60°旋转模型E;两阶退台中部60°旋转模型F。各模型沿高度方向均设置了11个测点层,且对应测点层高度相同。表1列出了试验模型基本参数。
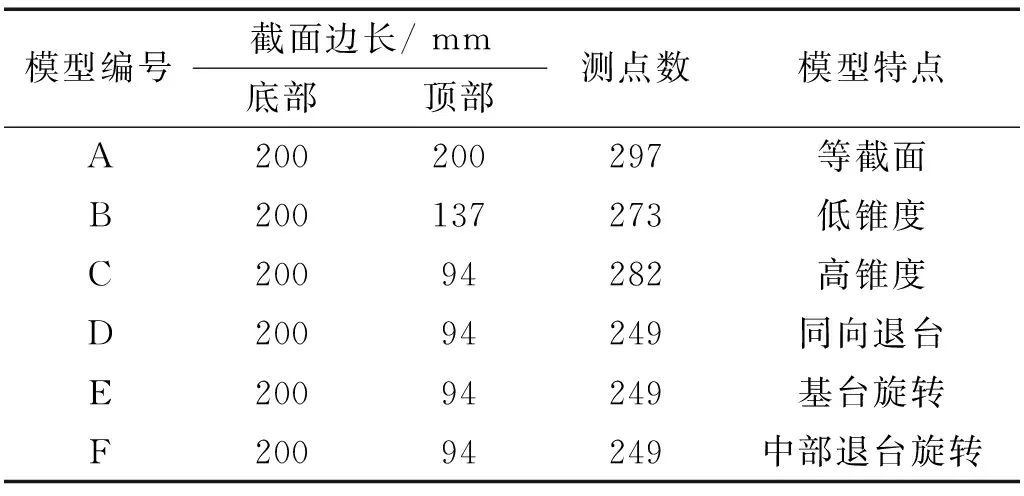
表1 试验模型基本参数Tab.1 Basic parameters of test models
为获得精细的风荷载特性随风向变化,各模型以5°为一个风向,在0° ~ 360°内分别设置了72个风向角工况。试验时模型顶部参考风速约10 m/s,测点采样频率f=312.5 Hz,采样长度为10 000次。图3给出了试验模型及风向示意图,以模型A为例,0°风向下处于圆角迎风,30°风向下处于不对称迎风,60°风向下处于弧面正向迎风。
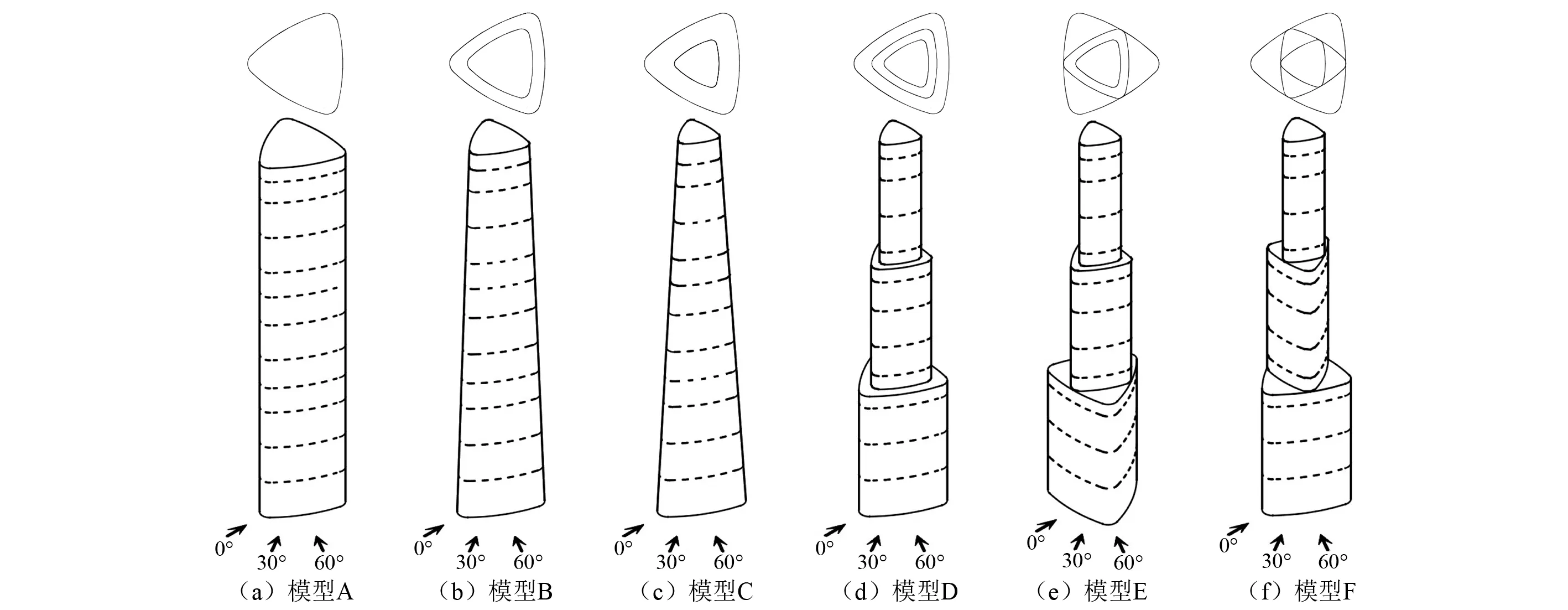
图3 试验模型及风向Fig.3 Test models and wind directions
为了消除试验风速和模型尺寸的影响,通过处理试验数据获得了各模型无量纲气动力系数,并采用CD,CL,CMZ,CML分别表示阻力系数、升力系数、扭矩系数和横风向基底弯矩系数。基底气动力系数定义为
(1)
(2)
(3)
(4)
式中:ρ为空气密度;UH为模型顶部风速;FD,FL分别为顺风向和横风向基底合力;MZ,ML分别为扭转向和横风向基底弯矩;A为迎风面投影面积,B0.5H为模型中部宽度。
2 试验结果分析
2.1 三分力系数
特殊的截面特性使圆角弧边三角形建筑在不同来流方向上呈现出截然不同的气动力特性。为研究顺风向、横风向和扭转向风荷载的分布特性,图4~图6分别给出了各模型阻力系数、升力系数以及扭矩系数的均值和均方根值随风向θ的变化趋势,图中数据为三个面试验结果的平均值。同时,引用2011年Kumar等研究中关于三棱柱的试验结果,以比较同等城市地貌下不同截面类型模型的试验结果。
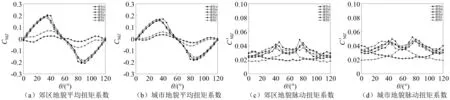
图6 扭矩系数随风向变化Fig.6 Variation of torsional moment coefficients on wind directions
从图4可以看出,两种地貌试验结果分布规律接近,城市地貌下,各模型平均阻力系数有所减小,而脉动阻力系数则由于来流湍流激励的增强而呈现增大。以城市地貌为例,各模型平均和脉动阻力系数均在0°~35°内缓慢增长,之后则迅速增大,说明圆角弧边三角形建筑在圆角迎风和弧面迎风时气动力特性差异较大;相比之下,三棱柱建筑的平均和脉动阻力系数则从20°起开始迅速增大,并大幅超过其他模型的阻力系数值。究其原因:当弧面迎风时,三棱柱建筑的尖锐拐角使气流分离位置更为稳定,降低了阻力系数对不同迎风方向的敏感性;而圆角处理使气流分离位置不断向后移动,有利于减小平均和脉动阻力系数。
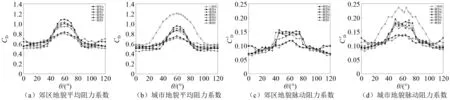
图4 阻力系数随风向变化Fig.4 Variation of drag force coefficients on wind directions
等截面模型A平均阻力系数在60°风向下达到最大值,随着锥度增加,平均阻力系数逐渐减小,而同向退台模型D平均阻力系数则进一步减小。然而,这4个模型的脉动阻力系数在弧面迎风一定范围内数值接近,并由于脉动风的不确定性而上下波动,说明锥度化和同向退台对脉动阻力系数的改善效果甚微。相比之下,底部旋转模型E和中部旋转模型F的平均和脉动阻力系数在弧面迎风时都比较小,这是由于两种退台旋转方式使部分高度范围内的弧面迎风转为圆角迎风,大大降低了顺风向风荷载。以郊区地貌为例,随着锥度增加,模型B和模型C的平均阻力系数降幅分别为5.5%和8.2%,同向退台模型D平均阻力系数降幅达到13.8%,而底部旋转模型E和中部旋转模型F的平均阻力系数降幅甚至达到25%左右。
图5表明,相比于郊区地貌,城市地貌下各模型平均升力系数减小,除模型A之外的其余模型脉动升力系数略微增大。郊区地貌下,模型A脉动升力系数从35°风向起迅速增大,并在60°风向达到最大值0.30;而在城市地貌下,模型A脉动升力系数曲线在60°风向左右较为平缓。这可能是由于模型A在郊区地貌60°风向下出现最强烈的漩涡脱落现象,而城市地貌下的风场抑制了漩涡脱落,从而降低了该风向下的脉动升力系数。与模型A相比,三棱柱建筑的升力系数峰值所对应的风向范围不同,其平均升力系数峰值略微减小,脉动升力系数峰值则大幅减小28%左右,说明圆角处理反而会增大平均升力系数和脉动升力系数。
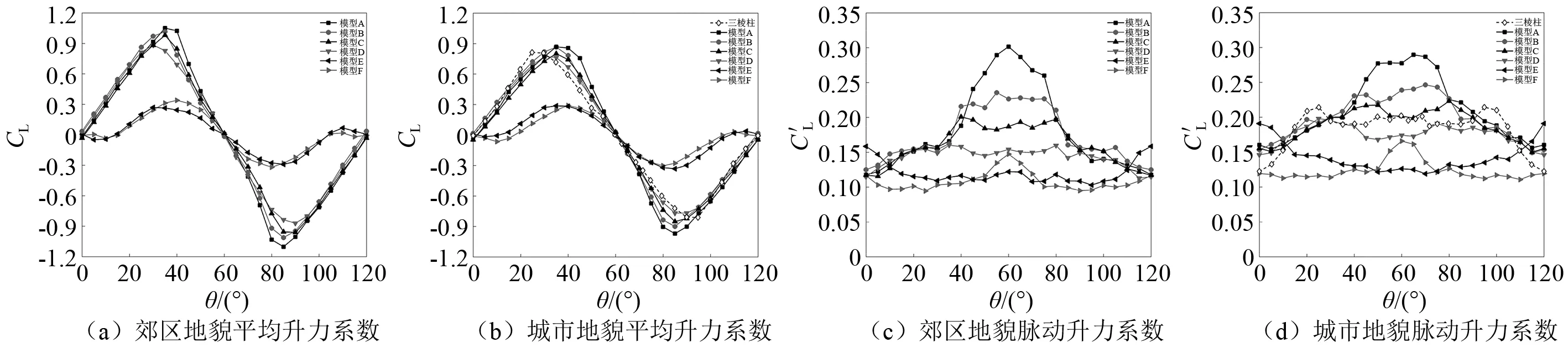
图5 升力系数随风向变化Fig.5 Variation of lift force coefficients on wind directions
模型A~模型D平均升力系数峰值出现在35°和85°风向附近,而脉动升力系数峰值主要出现在弧面迎风附近。可以看出,锥度化可以降低平均升力系数,并大幅减小脉动升力系数,且锥度越大,效果越好,但总体效果差于退台的效果。相比之下,模型E和模型F平均升力系数远小于其余几个模型,说明退台旋转可以进一步降低平均升力系数。然而,模型E和模型F脉动升力系数峰值大小则接近模型D,其中,模型E脉动升力系数峰值出现在0°风向,模型F脉动升力系数峰值集中在60°风向附近,说明退台旋转可以改变脉动升力系数峰值对应的风向范围。以郊区地貌为例,低锥率模型B、高锥率模型C和同向退台模型D的平均升力系数降幅分别为4.1%,7.0%和16.5%,而两种退台旋转模型的平均升力系数降幅甚至达到70%左右。随着锥度增加,模型B和模型C的脉动升力系数降幅分别为21.7%和33.3%,三种退台模型脉动升力系数降幅则接近47%。
由图6可见,各模型的扭矩系数在数值上明显小于阻力系数和升力系数;城市地貌下平均扭矩系数较小,而脉动扭矩系数相对稍大。模型A~模型D平均扭矩系数峰值出现在35°和85°风向附近,这与平均升力系数分布规律类似;但脉动扭矩系数峰值对应的风向范围则与脉动升力系数不同,它出现在弧面迎风两侧40°和80°风向附近。由于锥度化和同向退台仅改变截面尺寸,未明显改变表面风荷载分布状态,因而对平均和脉动扭矩系数影响甚微。两种退台旋转方式对扭矩系数的影响规律与升力系数接近,能够大幅降低平均扭矩系数,并改变脉动扭矩系数峰值对应的风向范围。
2.2 横风向弯矩系数谱
图7给出了两种地貌下模型A在弧面迎风附近多个风向下的横风向弯矩系数功率谱密度,这里宽度B统一采用模型底面宽度,横坐标即为折算频率,纵坐标fSCML表示无量纲的横风向弯矩系数功率谱密度。可以看出,两种地貌下模型A均在60°风向发生最强烈的漩涡脱落现象,峰值对应的折算频率,即斯托罗哈数约为0.11。相较而言,郊区地貌下的功率谱从50°风向起就开始出现集中现象,且数值明显更大;而城市地貌下的功率谱在50°风向下未出现尖锐谱峰,且弧面迎风时的数值相对较小,说明城市地貌下的风场可以有效抑制弧面迎风时的漩涡脱落,进一步验证了郊区地貌下模型A脉动升力系数在60°风向明显更大的原因。
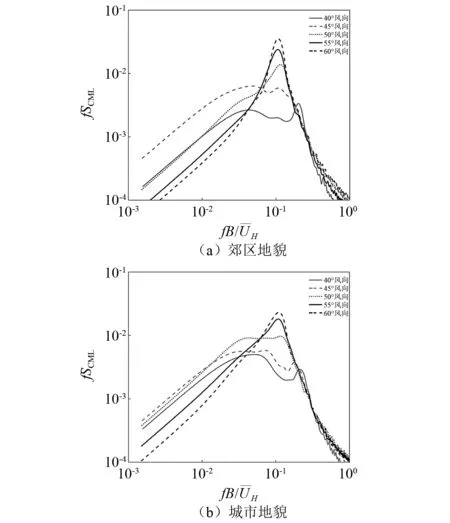
图7 模型A横风向弯矩系数功率谱密度Fig.7 Power spectral densities of across-wind overturning moment coefficients of model A
图8为两种地貌下各模型在60°风向下的横风向弯矩系数功率谱密度的比较。由图8可见,两种地貌下各模型功率谱分布规律相近。以郊区地貌为例,模型A功率谱集中程度最大,带宽最小,表明发生了最强烈的漩涡脱落。随着锥度的增加,模型B和模型C的功率谱曲线右移,带宽增大,峰值大幅减小。这是由于锥度化模型随着高度增加,迎风宽度逐渐减小,发生漩涡脱落的频率逐渐增大,从而产生一系列频率逐渐递增的局部漩涡,有效降低了功率谱峰值,且锥度越大,效果越明显。相比之下,同向退台模型D沿高度分为3种迎风宽度,总体上产生3组不同频率的局部漩涡,且不同频率漩涡由于频率相差较大,彼此的相关性较低,导致功率谱峰值更低。然而,值得注意的是,底部旋转模型E的功率谱在折算频率较小时明显最小,但在0.16折算频率附近超过模型D;中部旋转模型F的功率谱在0.1~0.2折算频率范围大幅减小,而在0.28折算频率附近超过模型D,表明两种退台旋转方式抑制了模型旋转部分所对应的局部漩涡,却明显增大了上方相邻退台部分的漩涡脱落程度。
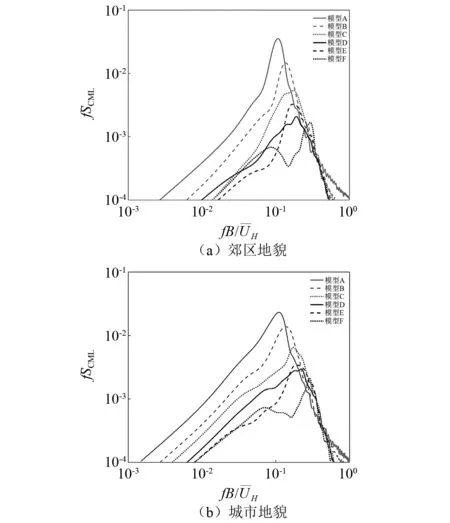
图8 60°风向下横风向弯矩系数功率谱密度对比Fig.8 Comparison of power spectral densities of across-wind overturning moment coefficients
2.3 层脉动升力系数谱
为进一步分析两种退台旋转方式对不同高度各部分漩涡脱落的影响,图9、图10分别给出两种地貌中部及上部退台层脉动升力系数功率谱沿高度分布,纵坐标fSCFL表示无量纲的层脉动升力系数功率谱密度。其中:第4~第7测点层位于中部退台;第8~第11测点层位于上部退台。可以看出,两种地貌下,对应高度测点层的层脉动升力系数功率谱分布规律类似。
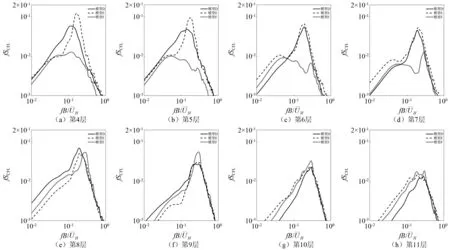
图9 郊区地貌层脉动升力系数功率谱密度Fig.9 Power spectral densities of layer lift force coefficients under suburban landforms
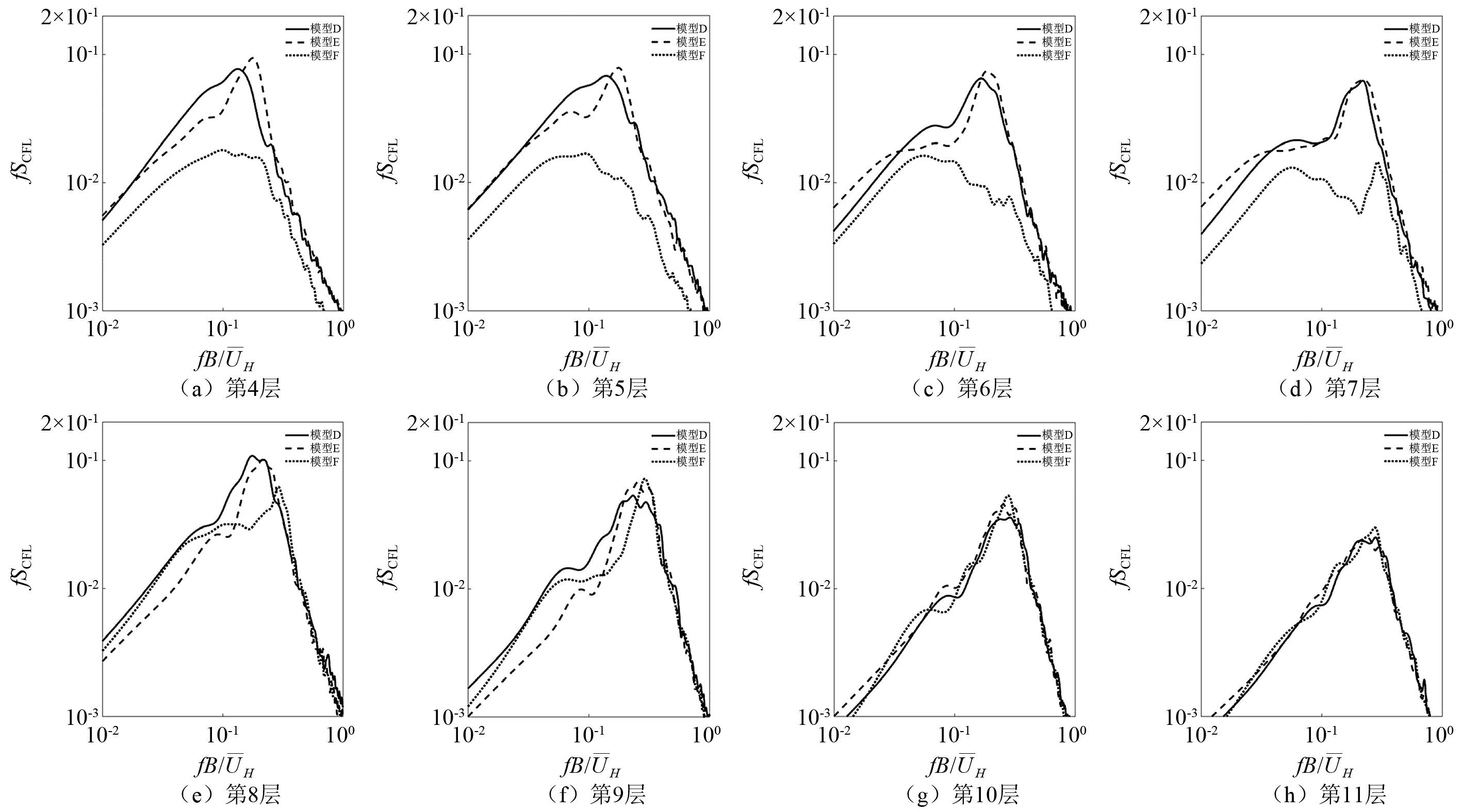
图10 城市地貌层脉动升力系数功率谱密度Fig.10 Power spectral densities of layer lift force coefficients under urban landforms
在中部退台上,模型D第4、第5测点层升力系数功率谱受基台影响,带宽较大,而第6、第7层功率谱集中现象更明显。模型E功率谱明显大于模型D,且距离基台越近,功率谱相对更大,说明基台旋转使模型E中部退台漩涡脱落程度明显增强。其原因在于,模型E基台旋转后处于圆角迎风,气流在基台两侧风弧面上逐渐加速,而中部退台漩涡脱落位置处于基台两侧风弧面中部所在的竖直面上,这样基台上加速的气流就会对中部退台的漩涡脱落产生增强效果。模型F由于中部退台旋转,其第4~第7层功率谱明显最小,第7层功率谱则由于上部退台漩涡脱落的影响在0.28折算频率附近产生集中趋势。
在上部退台上,可以看出模型D和模型E各层功率谱峰值较为接近,并随高度增加而逐渐减小。同时,受中部退台漩涡脱落影响,模型D和模型E第8层功率谱峰值对应的折算频率仍在0.20左右。模型F第8层功率谱则在0.28折算频率处明显集中并超过模型D和模型E,第9~第11层功率谱峰值同样由于中部退台两侧风弧面上气流加速的影响而明显最大,进一步说明两种退台旋转方式能够明显增强上方相邻退台部分的漩涡脱落程度。
3 结 论
以圆角弧边三角形超高层建筑为对象,采用同步测压风洞试验方法研究了郊区地貌及城市地貌下几种立面优化措施:锥度化、同向退台以及两种退台旋转对建筑三分力系数、基底横风向弯矩系数功率谱和层脉动升力系数功率谱的影响。通过对比分析,可以得出如下结论:
(1) 与郊区地貌相比,城市地貌下各模型三分力系数总体上呈现出平均分力系数减小,脉动分力系数增大的变化趋势。然而,等截面模型A脉动升力系数在郊区地貌弧面正向迎风时明显更大,这主要由强烈的漩涡脱落所致。城市地貌下的风场可削弱其漩涡脱落,从而降低脉动升力系数。
(2) 锥度化和同向退台均可有效降低平均阻力系数、平均升力系数和脉动升力系数,且降幅随锥度增大而增大;相比之下退台的效果更佳;两种措施对脉动阻力系数的影响很小;因锥度化和同向退台未明显改变风荷载分布状态,故对平均和脉动扭矩系数影响甚微。与同向退台相比,退台旋转方式能更有效降低三个平均分力系数和脉动阻力系数,并改变脉动升力系数和脉动扭矩系数峰值对应的风向范围。
(3) 随着锥度增大,横风向弯矩系数功率谱峰值频率右移,谱峰降低;同向退台也呈现类似影响,但程度更大。两种退台旋转会使功率谱部分频段的能量明显超过同向退台情况,这是由于当旋转部分圆角迎风时,在两个侧风弧面上加速的气流会对上方相邻退台的漩涡脱落产生增强效应。

