基于混沌序列的电力营销数据去隐私化加密方法研究

江元， 李晓明， 尚云飞

(1.国网甘肃省电力公司， 甘肃,兰州 730030;2.国网甘肃省电力公司,营销服务中心， 甘肃,兰州 730030)

0 引言

网络信息安全问题日益严峻，极大影响了电力系统优质运行[1]。营销系统是信息管理类应用的核心业务系统，该系统能够生成、储存、处理及传输用户信息、用电信息等重要数据材料，具备很强的保密性，非法使用及泄露会给电力行业带来不可估计的严重损失[2]。通过多年的信息化建设实践证明，在开放、共享的网络环境内，电力营销数据依旧处在一种高风险状态，对其进行有效加密是十分迫切的发展需求。

文献[3]提出一种全同态数据加密聚合方案。运用DGHV全同态算法对隐私数据实施加密，同时把节点身份信息嵌入至数字签名中，令方案拥有追查并修复错误的能力。该方案无需可信第三方，以簇为单位分配干扰因子，从而抵御内部攻击并提高运行效率。但该方法计算速率较慢，即时性不高。文献[4]以船舶通信网络为例，针对无法实现身份数据认证而造成加密权限紊乱问题，设计一种基于身份认证的船舶通信网络全同态加密方法。运用汇聚节点方法把身份认证程序代入全同态加密系统内，经过明文集计算对身份认证数据采取同态加密，检测汇聚节点数据实现身份认证检测；对加密文案进行去噪，通过整数同态加密达到船舶通信网络全同态加密目标。但该方法安全性能差，被破解概率较高。

本文总结上述方法缺陷，提出一种基于混沌序列的电力营销数据去隐私化加密方法。通过评估电力营销数据隐私风险系数，了解电力营销数据潜在安全隐患；阐明混沌序列加密原理，使用基于Logistic混沌序列的数据加密模型，完成高精度、高效率的电力营销数据加密目标。

1 偏联系数下电力营销数据隐私风险评估

数据隐私风险评估就是对数据风险采取全方位的评判与衡量。隐私风险即为数据产生泄露的可能性与后续带来的负面影响[5]。

联系数是描述2个集合互相关联、制约并凸显属性的同、异、反关系解析式[6]。假设Z是一个非空集，那么A={〈z,aAz,bAz,cAz〉z∈Z}的联系数为式(1),

μAz=aAz+bAzi+cAzj

(1)

式中，aAz、bAz、cAz依次为Z内元素z隶属A的支持度、不确定度与对立度。

式(1)中包含同、异、反3个因子，所以又将其叫作三元联系数。对三元联系数内的不确定值度b(2)实施进一步计算，得到一般形式式(2),

μ=a+b1i1+b2i2+…+bnin+cj

(2)

偏联系数是表示偏离走势变化高低的一种函数，折射出同异反联系形态的发展趋势与变化[7]。在电力营销数据隐私风险评估过程中，同势代表隐私风险评估和预期标准风险接近于相同变化形态，也就是处在隐私评估的低风险区域；均势代表隐私风险评估和预期标准风险水准差距略高，处在隐私评估的中级风险区域；反势代表隐私风险评估和预期标准风险是相反状态。处在隐私评估的高风险区域。

五元联系数μ的记分函数表示成式(3),

Sμ=a+b-d+e

(3)

五元联系数μ的精确函数为式(4),

Hμ=a+b+d+e

(4)

记分函数Sμ与精确函数Hμ类似于数据统计内的均值与方差，记分函数越高，数据隐含风险越大；记分函数越低，其风险指数越小。在记分函数相等的情况下，精确函数越高，数据风险越大，反之越低。所以，本文使用记分函数与精确函数对电力营销数据的隐含风险实施等级排列预测[8-9]。

权重是数据隐私风险评估时，可以呈现出每个待评估指标影响力度的数值。本文融合主观赋权与客观赋权，设计一种五元偏联系数势的最小二偏赋权方法[10]。

关于隐私风险属性Gi，将其r阶偏联系数势矩阵描述成式(5)：

(5)

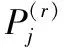
(6)

式(6)仅代表权重关键水平相等的状态。一般情况，数据隐私风险指标的权重关键水平是互不相等的。在不同权重矢量Wi组成的评估指标内，想要了解评估结果的适用性，就要建立最小二偏函数为式(7)：

(7)

组建Lagrange函数对上式进行计算，获得最小h偏赋权解析式为：

(8)

2 混沌序列加密过程分析

混沌现象为非线性确定性系统内的一种随机过程，将2个特别接近的原始值引入相同混沌函数实施迭代计算，通过特定阶段的计算后，数值序列没有任何相似性[11]。此种加密方式隶属于确定性系统，但很难对其进行预判，隐藏在冗杂系统内却又无法分解。

混沌信号的非周期性、持续宽带频谱、与噪声相似等特征，令其具备天然的隐蔽特性，对原始条件高度敏感，拥有长期的不可预测性[12]，让数据很难遭受恶意侵害与攻击。

Logistic映射表示非线性混沌方程，其映射过程为式(9)：

Xn+1=bXn1-XnXn∈0,1

(9)

式中，b代表控制参变量。明确b的具体数值后，通过随机原始值X0∈0,1能够迭代计算出一个明确的时间序列X1,X2,…,Xn。

混沌序列加密的安全性关键依赖混沌密钥流，在混沌加密系统内，把混沌系统生成的随机序列xi>当作密钥流ki>和明文数据流mi>的按位运算，继而得到密文数据流ci>。明文数据流为二进制，而密钥流ki>是对混沌序列xi>实施数据处理得到的。采用计算机技术对初始混沌数据xi>进行多类处理，让其在有限计算准确度前提下，完成混沌序列的随机性。

混沌加密密码作为一种序列密码。混沌序列密码系统的加密端与解密端为2个完全独立且相等的混沌系统，2个系统之间没有耦合关联[13]。明文数据在加密端加密后直接传输到解密端，解密端能够在全部接收后再实施解密。混沌序列密码加密方式较为灵活，能够有效运用混沌信号的特征获得结构复杂的加密函数。混沌序列密码系统如图1所示。

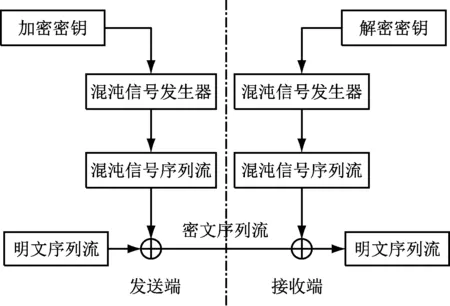
图1 混沌加密过程

3 混沌序列下电力营销数据去隐私化加密

通过混沌序列转变原有数据，让没有授权的用户即便得到已加密数据，但由于无法进行解密，依旧不能明确信息内容的方法,由此最大程度保障数据安全，预防数据外泄现象发生。同时在加密前将数据去隐私化能更有效提升数据安全性。

将式(9)模式的Logistic映射产生的序列概率分布函数记作式(10)：

(10)

使用ρx能够轻易获得Logistic映射生成的混沌序列某些具备重要作用的统计特征，例如x的平均时间，也就是混沌序列轨迹点平均值，描述为式(11)：

(11)

针对互相关函数来说，单独挑选2个原始值x0与y0，那么序列互相关函数为式(12)：

(12)

序列的自相关函数ACF和delta函数相等。

因为去隐私化加密对象是数字量，因此把通过实数组成的序列xk>映射为经过整数组建的伪随机序列，完成去隐私化目的，并将其作为加密密钥，使用的映射方式为挑选小数点后几位有效数字组合为整数，构建一种Logistic混沌映射选的加/解密模型，如图2所示。完整的加/解密运算方法如图3所示。

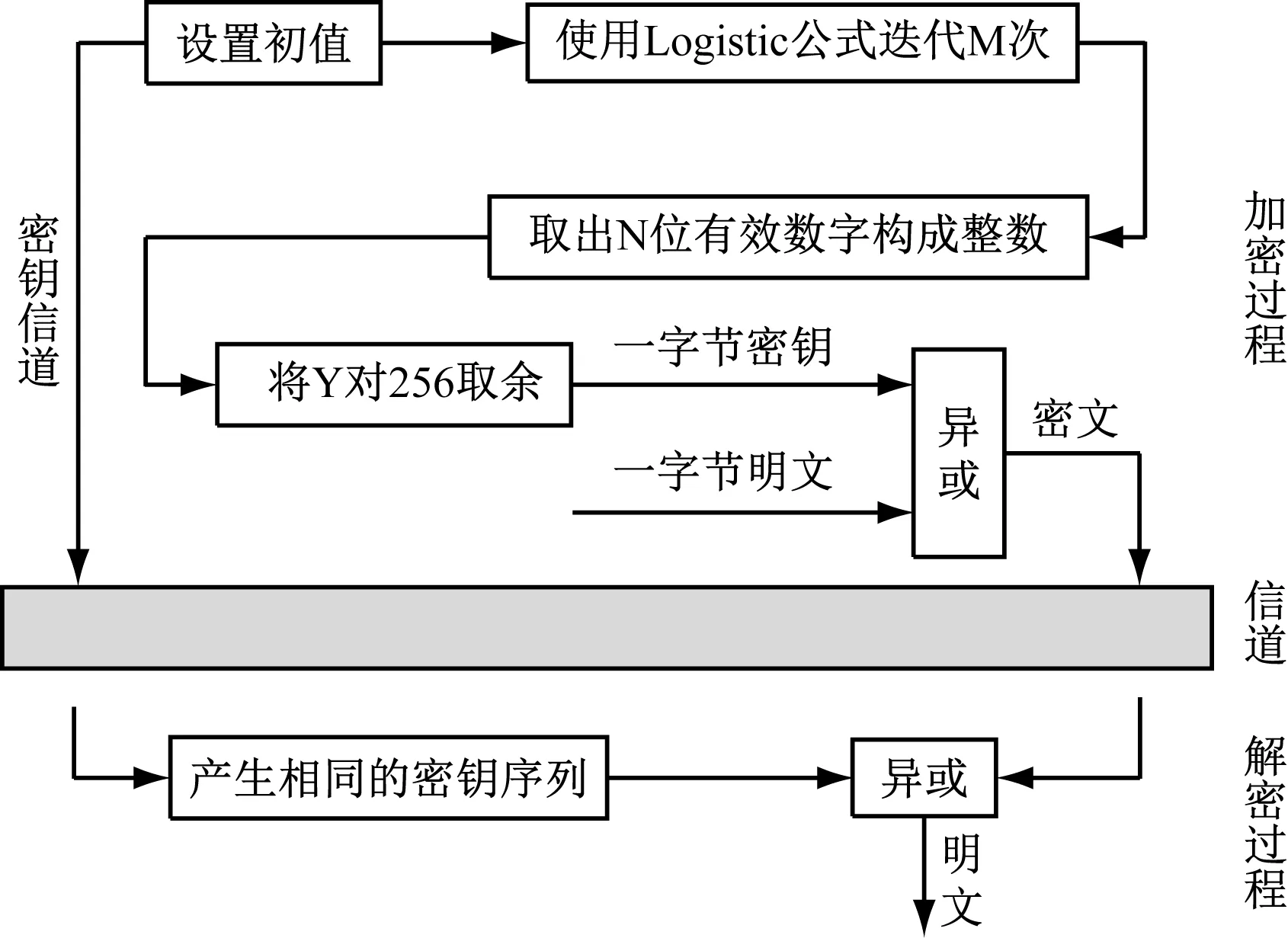
图2 混沌序列加密模型示意图

为了让序列更具随机性，同时提升其加密速率，随机数值择取的间隔M等于6是最为恰当的。Yk的值是Xk小数点后3、4、5位，这样就会增强抗选择明文攻击性能。

为了提升明文攻击适应度，对Xn实施数据处理，让Xn和Xn+1二者间的关系更加复杂，继而防止攻击者使用简单的推导过程求解出μ值。本文使用间隔取数手段，在Xn和Xn+1之间安置一个数值，那么Xn和Xn+1的关联式转变为式(13)：

(13)

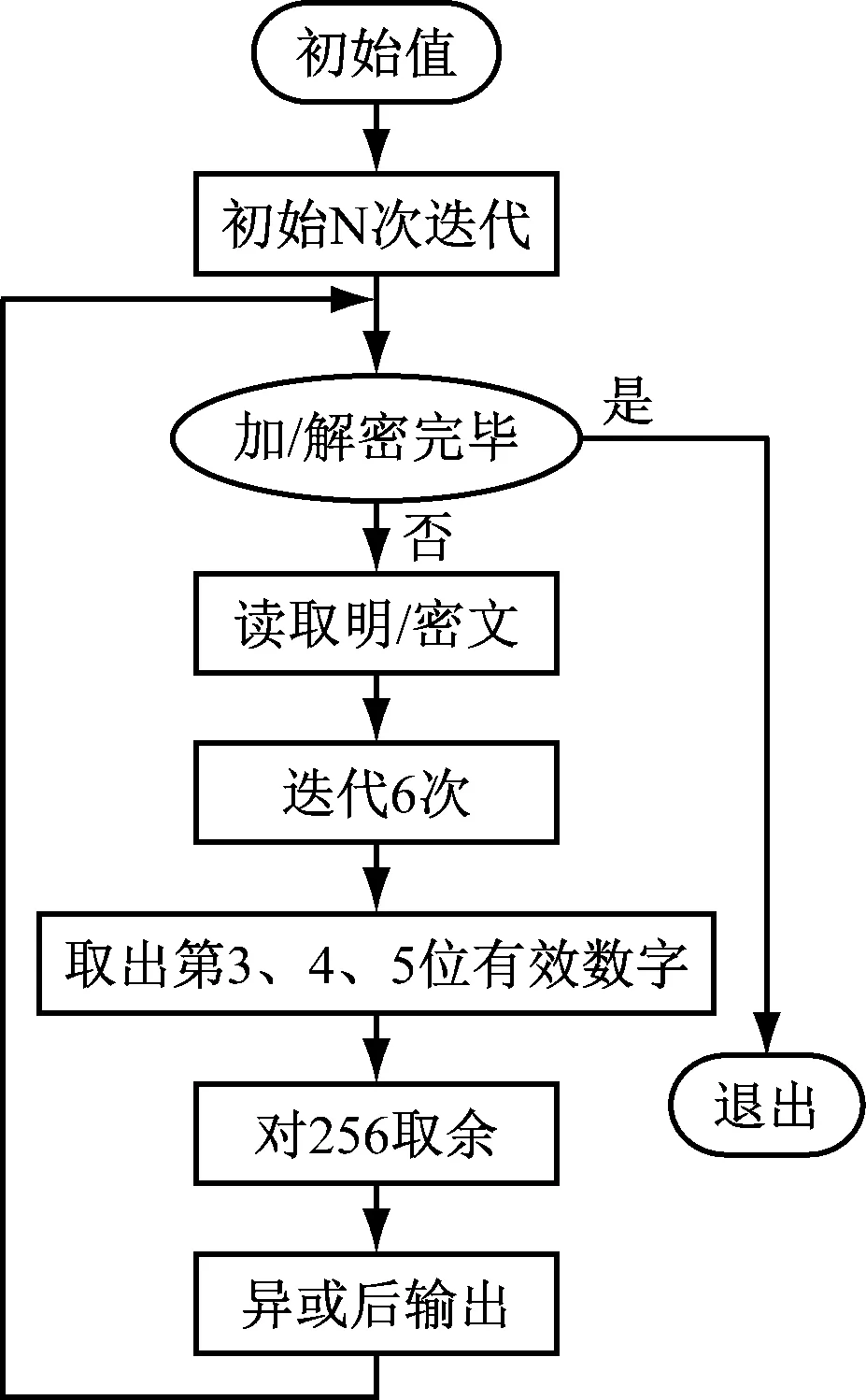
图3 混沌加密/解密方法架构图

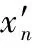
为了不暴露明文信息冗余度，加密体制需要充分且匀称地使用密文空间，混沌序列也要明确加密后密文数据的统计分布状态，也就是明文数据是否被全部掩盖，这也是权衡加密方法有效性的关键准则。如果密钥序列是完全随机状态，那么加密之后的密文数据顺从匀称分布。将明文与密钥序列当作一个字节的数据流，从中任意选取一个字节的明文m与密钥k。假设m取值是不相等的，也就是某一位出现0或1的几率是不同的，并且数据位出现0或1是互相独立事件。若明文第i位出现1的几率是p，密钥序列在理想情况下符合白噪声性，也就是产生0或1的求元率是相同的，都是0.5。那么加密后密文c的第i位出现1的求元率为式(14)：

(14)

因此可以看到，加密后密文的求元率分布是匀称的，也就完成了电力营销数据去隐私化加密目标。某电力企业数据库内部分电压输出原始数据如表1所示。采用本文方法得到的电压输出原始数据去隐私化加密后的模式如表2所示。

4 仿真实验

按照本文方法计算步骤，将Logistic当作例子，探究混沌序列加密的真实效用，对其进行电力营销数据去隐私化加密及解密仿真。

对相同明文使用两组略有差别的原始密钥依次加密后的密文字符ASC码值分布示意图如图4所示。圆点线代表明文，正方形点线对照x0值为0.600 01加密后获得的密文字符，μ=3.74。从图4可知，相同的明文在密钥产生细小改变时，明文会发生明显改变，折射出密文对密钥的敏感特征。

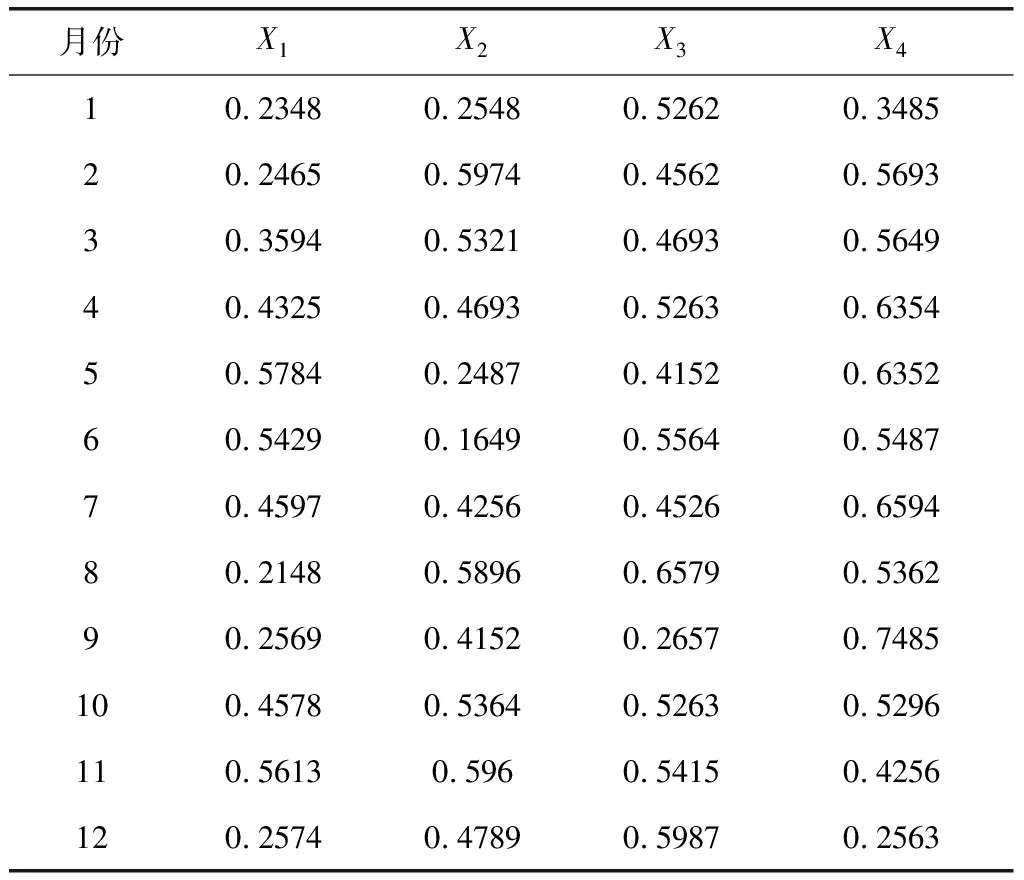
表1 电压输出原始数据

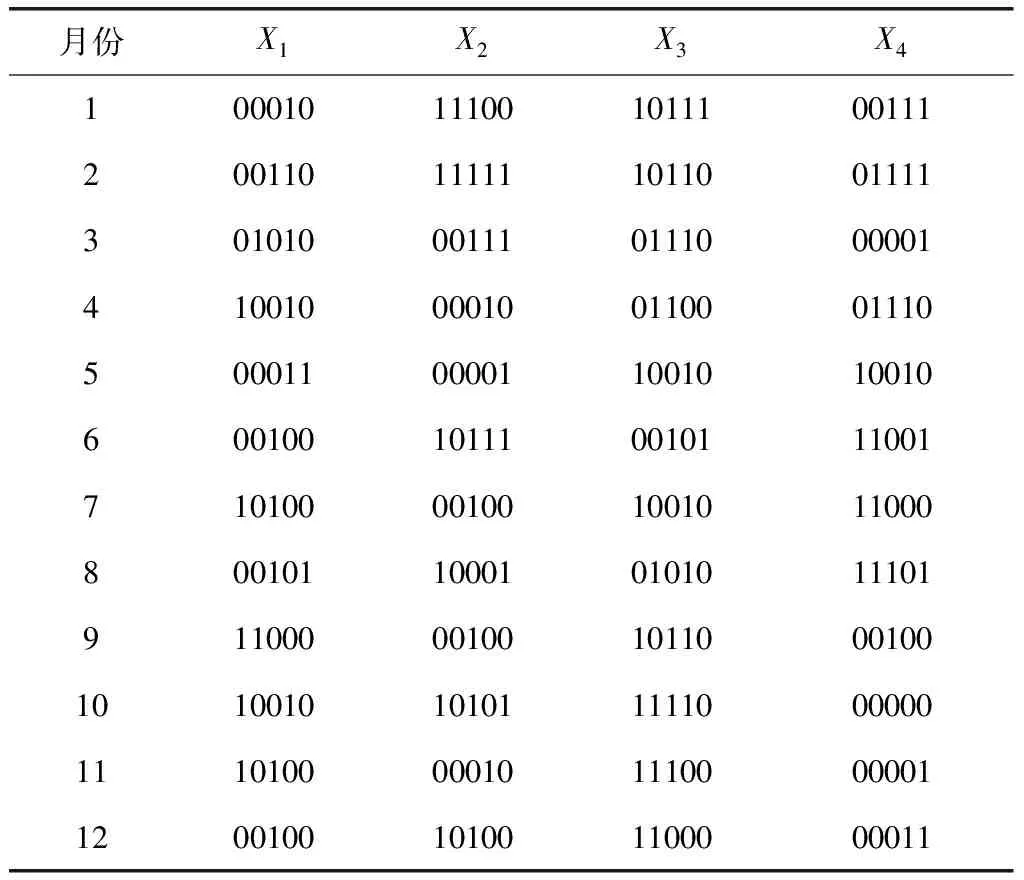
表2 电压输出去隐私化加密数据

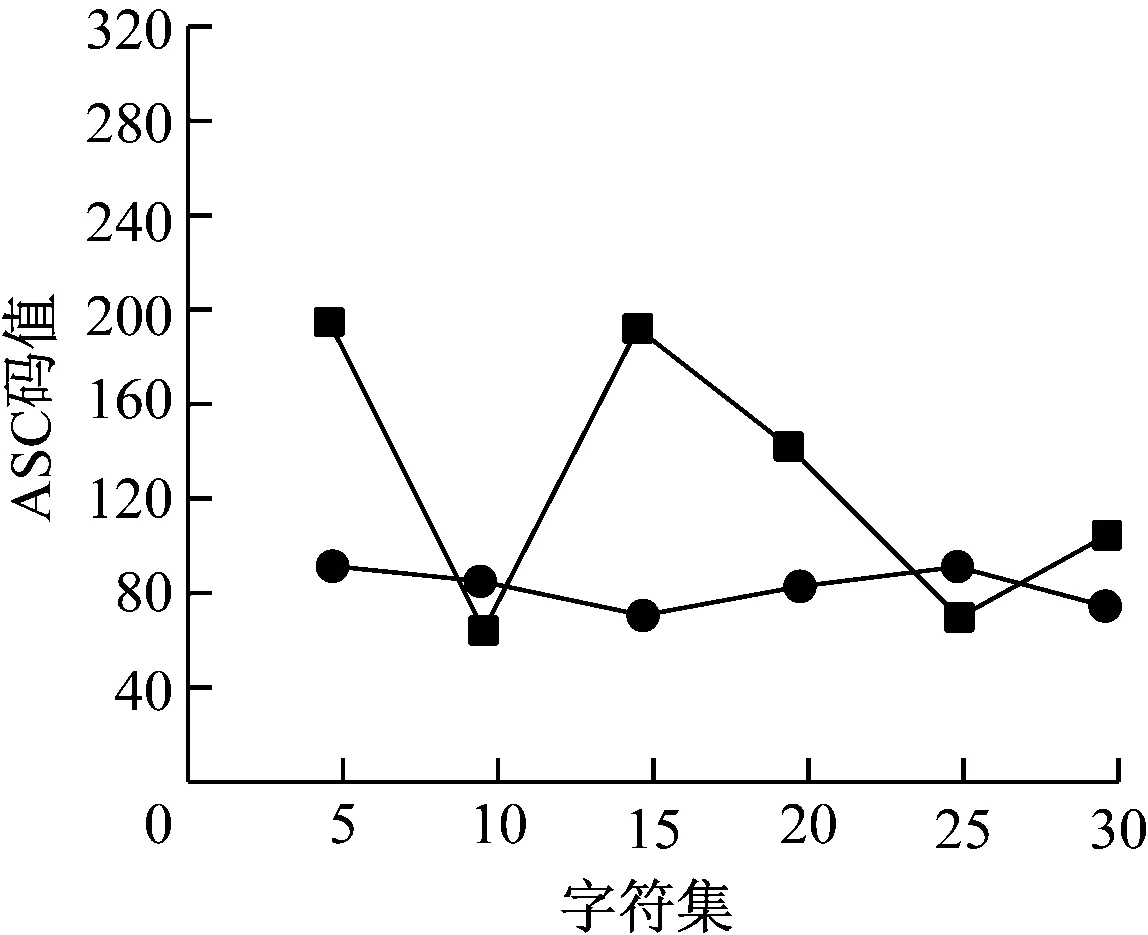
图4 密文字符ASC码值分布示意图

本文加密方法的迭代次数分布状况如图5所示。从图5可知，迭代次数集中发生在220-620之间，降低了迭代次数，提升了加密方法的计算速率与计算开销。

为了进一步验证本文方法加密性能可靠性，依次与文献[3]和文献[4]进行仿真对比，对某企业电力营销数据进行加/解密操作。测验环境是奔腾3.0GHzCPU，2GB内存。获得3种方法性能对比如表3所示。从表3可知，本文方法的解密效率与迭代次数均优于2个文献，由此证明了本文方法数据加密优越性。

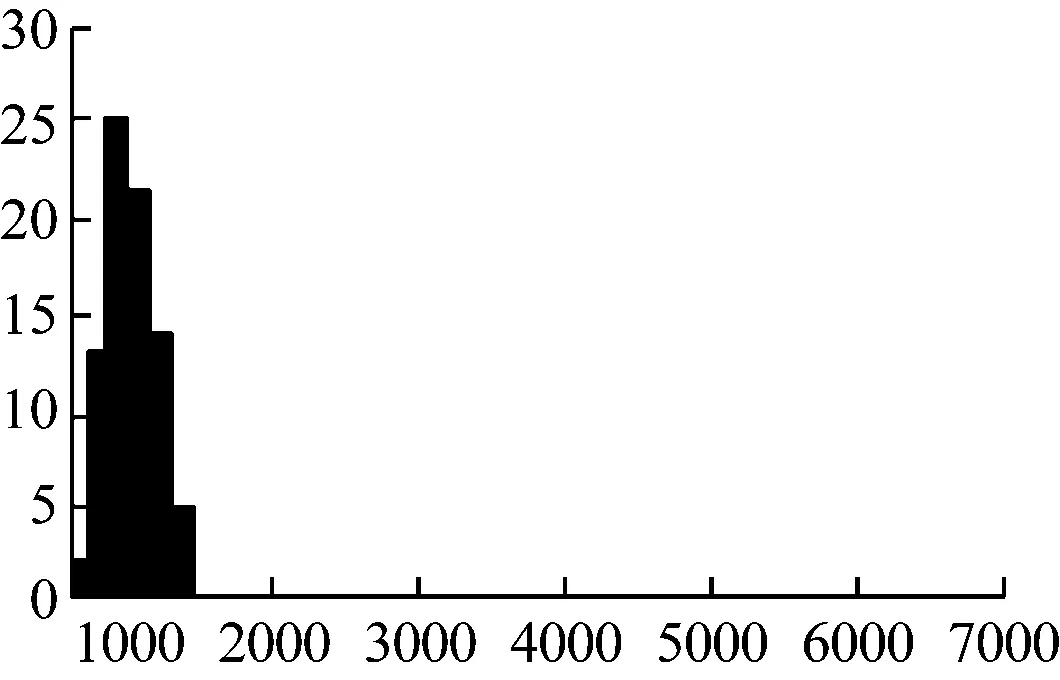
图5 本文方法迭代次数分布示意图

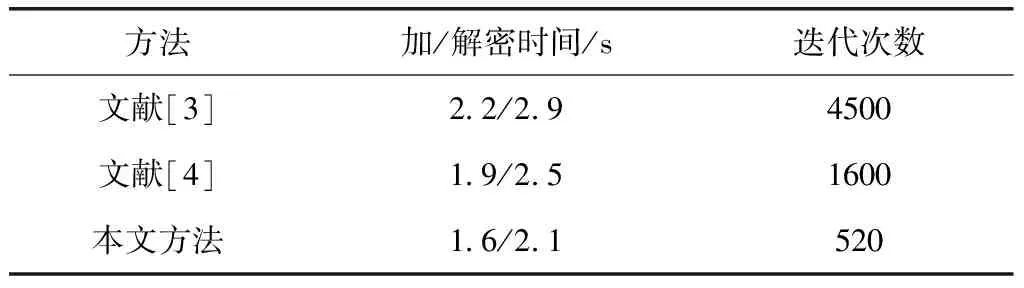
表3 加密方法性能对比

为了进一步验证不同方法的抗攻击能力，在一定强度的攻击下，采用WSN加密方法、身份认证加密方法以及混沌序列的加密方法对数据丢包率进行检测，结果如图6所示。

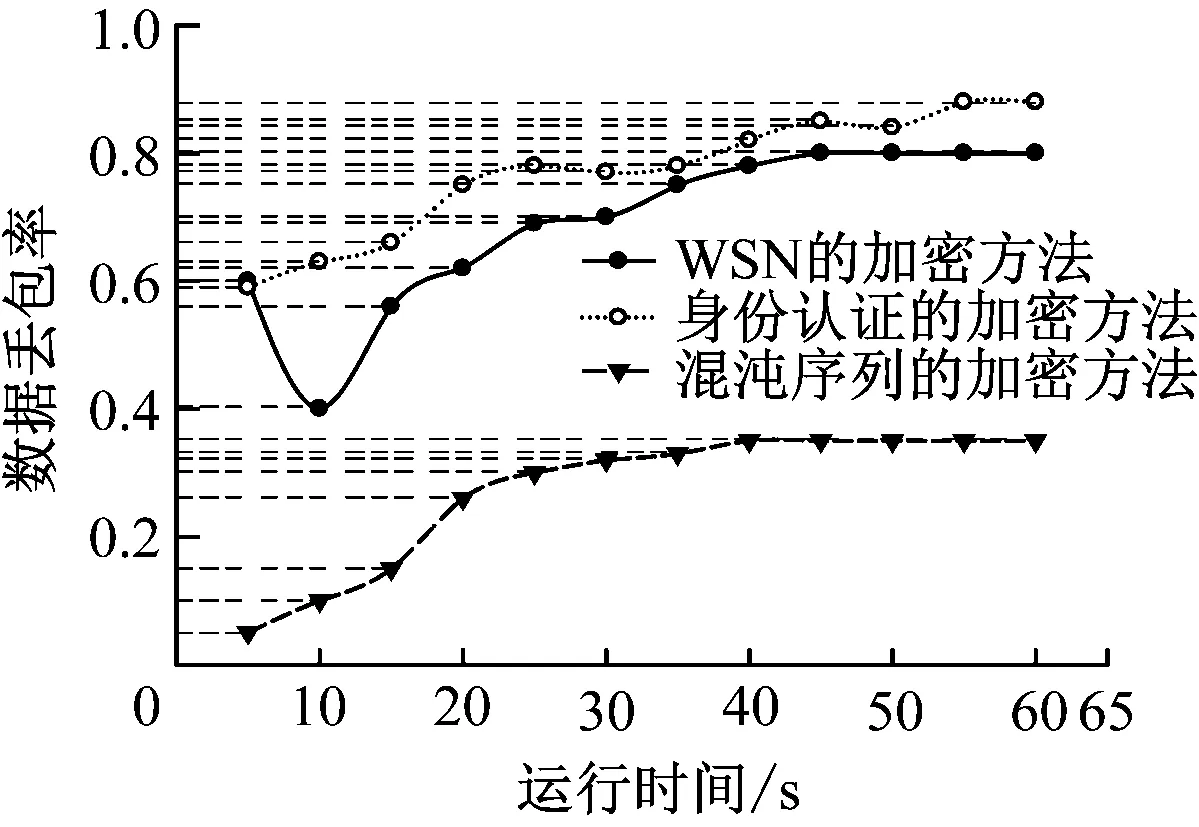
图6 不同方法下数据丢包率

分析图6可知，当运行时间为10 s，WSN加密方法的数据丢包率为0.4，身份认证加密方法的数据丢包率为0.63，混沌序列的数据丢包率为0.10。当运行时间为50 s，WSN加密方法的数据丢包率为0.8，身份认证加密方法的数据丢包率为0.84，混沌序列的数据丢包率为0.35。本文方法的数据丢包率都较低，说明本文方法具有较强的抗攻击能力。

5 总结

使用混沌序列下的电力营销数据去隐私化加密方法，可提高电力营销数据安全性，同时规避了物理同步混沌系统面临的技术问题，完成电力营销数据精准加密，且抗攻击能力好，为满足信息化时代数据加密需求提供扎实基础。但该方法只能保护数据，无法防御恶意攻击行为，下一步研究方向即在加密的同时，对入侵行为进行检测和识别。