离散蝠鲼觅食优化算法及在频谱分配中的应用

王大为，刘新浩，李 竹，芦 宾，郭爱心，柴国强

（山西师范大学物理与信息工程学院，山西临汾 041004）

0 引言

近年来随着物联网、无线自组网、无人集群系统等技术的快速发展，无线通信业务量激增，导致频谱资源供给与通信业务需求之间的供需不平衡问题日益严峻［1-2］。频谱资源供给不足一方面是因为频谱作为国家的重要战略资源确实紧缺，而另一方面是由于传统预先划分的静态频谱分配方式所导致的频谱利用率低。2019 年，全球首届6G 峰会发表的《6G 无线智能无处不在：关键驱动与研究挑战》白皮书指出，6G 需要改变频谱使用规则，提升频谱资源利用率。认知无线电技术可动态探测无线环境，通过智能算法进行空闲频谱判断、发射机和接收机工作参数调整，让认知用户智能地接入暂时不被授权用户使用的“频谱空穴”，从而实现频谱资源的动态管理进而提高频谱利用率，被认为是解决频谱资源短缺问题的有效方法［3-4］。频谱分配作为认知无线电技术的重要环节起着限制认知用户和授权用户之间的干扰、提高网络效益的关键作用。而频谱分配问题可抽象为一个数学上的非确定性多项式难题的约束优化问题。到目前为止，有大量研究通过将图论着色模型［5］、博弈论模型［6］、定价拍卖模型［7］等经典数学模型以及人工智能算法与认知无线电技术相结合以解决频谱分配问题。例如遗传算法［8-10］、蚁群算法［11-13］、二进制粒子群优化（Binary Particle Swarm Optimization，BPSO）算 法［14-16］、离散人 工蜂群（Discrete Artificial Bee Colony，DABC）算法［17-19］等应用于解决该问题取得了不少成果。此外，在本文的前期研究中也提出了一种基于改进二进制粒子群优化（Improved Binary Particle Swarm Optimization，IBPSO）［20］的频谱分配方法来提高网络效益。但正如No Free Lunch Theorem of Optimization 定理［21］所言，没有通用算法可以完美解决所有实际工程问题。这些算法在解决认知无线电频谱分配时，特别是在用户数和可用频谱较多的大规模问题上，都难以避免地陷入局部最优。而蝠鲼觅食优化（Manta Ray Foraging Optimization，MRFO）算法是群智能算法领域的最新研究成果，由Zhao 等［22］受蝠鲼群体觅食过程中链式觅食、螺旋觅食和空翻觅食等行为的启发而于2020 年设计和正式提出，具有结构简单、参数少、全局探索能力强等特点，可有效避免传统启发式智能算法普遍存在的局部最优问题。然而该算法基于连续域提出，不能直接用于解决频谱分配问题。因此，本文基于Sigmoid 函数（Sigmoid Function，SF）离散法和异或算子提出了离散蝠鲼觅食优化（Discrete Manta Ray Foraging Optimization，DMRFO）算法。该算法的主要工作体现在进行离散化设计时，根据频谱分配问题的特点，通过定义蝠鲼运动速度和引入解的亲1 性策略自适应地平衡DMRFO 算法在二进制空间的探索能力和开发能力，使得DMRFO 算法在理论上更适用于解决认知无线电中的频谱分配问题。同时，实验结果也表明DMRFO 算法的收敛速度和收敛精度明显优于离散人工蜂群（DABC）算法、二进制粒子群优化（BPSO）算法和改进的二进制粒子群优化（IBPSO）算法。

1 MRFO算法

1.1 标准MRFO算法

MRFO 算法是Zhao 等［22］于2020 年提出的一种新的群智能算法。该算法受蝠鲼觅食行为的启发分为链式觅食、螺旋觅食和空翻觅食三个过程，能有效避免传统启发式智能算法普遍存在的局部最优问题。

1）链式觅食（Chain foraging）。

蝠鲼群体觅食时，每个蝠鲼会跟在另一个蝠鲼后面形成一条觅食链，雄性蝠鲼被较大的雌性蝠鲼驮着并配合着雌性蝠鲼胸鳍舞动节拍在雌性蝠鲼的背部上空游动，以保证前面蝠鲼错失的食物源会被后面的蝠鲼捕捉到，从而提升群体的觅食效益。在MRFO 算法中，某一位置的食物浓度越高则该位置越好。虽然当前时刻还不知道最佳食物源的位置，但假设目前已知的食物浓度最高的位置为最佳食物源，蝠鲼观察并游向最佳食物源。在游动过程中，第一个蝠鲼向最佳食物源移动而其他蝠鲼同时向最佳食物源和它前面的蝠鲼移动，从头到尾排成一行形成一条觅食链。即在每次迭代过程中，每个蝠鲼按照目前找到的最佳食物源位置和它前面的蝠鲼更新自己的位置。链式觅食过程的数学模型可表示如下：

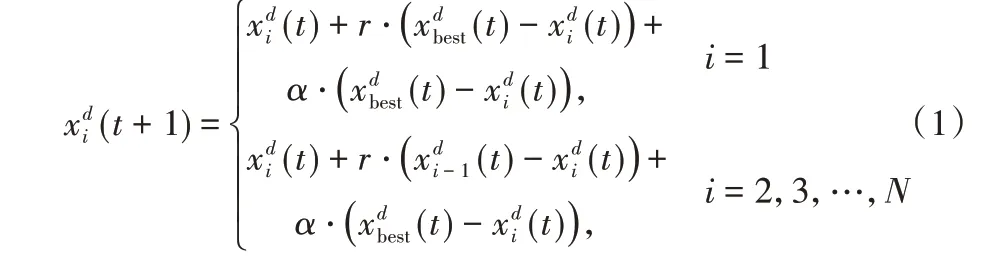
其中：(t)表示第i个蝠鲼t时刻所在位置的第d维参数；r为服从［0，1］均匀分布的随机数；α=2 ·r是权重系数(t)表示目前发现的最优食物源位置的第d维参数。第i个蝠鲼的位置更新取决于第i-1 个蝠鲼的位置和目前发现的最优食物源的位置xbest(t)，而第1 个蝠鲼的位置更新策略取决于最优食物源的位置。需要特别说明的是，如果把蝠鲼运动的物理空间和MRFO 算法的搜索空间对应，则蝠鲼的位置xi(t)就是搜索空间中的解，最优食物源的位置xbest(t)就是搜索空间中的最优解。

2）螺旋觅食（Cyclone foraging）。

当某个蝠鲼发现深海中的优质食物源时，蝠鲼群体中每个蝠鲼会首尾相接螺旋式向食物源聚集。聚集过程中蝠鲼群体的运动方式由单纯的链式运动转变为围绕最优食物源的螺旋运动。螺旋觅食过程可用如下数学模型表示：

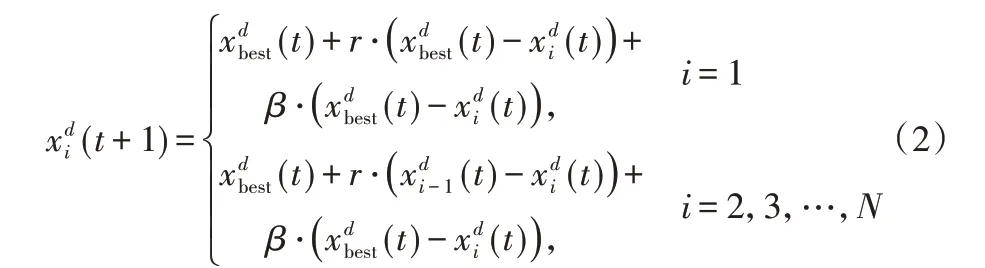
其中：β=2er1(T-t+1)/T· sin(2πr1)表示螺旋运动的权重系数，T表示最大迭代次数，r1代表旋转因子，为服从［0，1］均匀分布的随机数。蝠鲼群体根据该式在最优食物源附近螺旋式随机搜索，因此螺旋觅食过程对最优解附近的区域有较好的开发性能。此外，为了强化算法的搜索性能，可以随机产生一个新位置（解），然后在该位置附近执行螺旋觅食操作，其数学模型式如下：

其中是在搜索空间中随机产生的一个新位置（解）。

3）空翻觅食（Somersault foraging）。

当某个蝠鲼发现食物源后，将食物源视作一个支点并绕支点旋转、空翻至一个新位置，以引起其他蝠鲼的注意。对蝠鲼群体而言，空翻觅食是一个随机的、局部的和频繁的动作，它可以提高蝠鲼群体的觅食效益，其数学模型如式（4）：

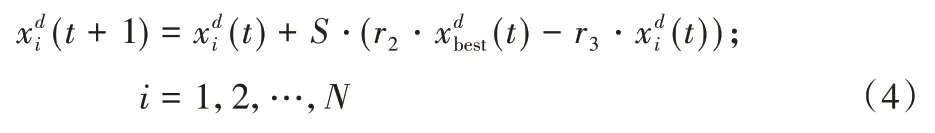
其中：S是空翻因子，决定空翻的距离；r2和r3是服从［0，1］均匀分布的两个随机数。随着S取值不同，蝠鲼个体会空翻至搜索空间中和当前位置关于最优解对称的位置。如果当前位置和最优解相距较远，则空翻后位置与最优解相距也较远，表征着对搜索空间的探索；如果当前位置和最优解相距较近，则空翻后位置与最优解也较近，表征着对最优解附近空间的开发。

1.2 离散MRFO算法设计及分析

MRFO 是针对连续空间函数优化问题设计的，为解决工程中的频谱分配问题须对蝠鲼觅食优化算法进行离散化处理。此外，由于频谱分配问题中仅有｛0，1｝两种状态，故本文主要探索如何将适用于连续空间的MRFO 算法离散为二进制空间的优化算法。因此，在对MRFO 算法离散化的过程中需满足两点：首先是要保留觅食行为的不变性，即将连续空间中的觅食行为映射到二进制空间后相应的觅食动作应保持不变；其次是搜索空间应和待解决的实际问题相匹配，即搜索空间的一个解（位置）对应着解决问题的一种方案。在MRFO 算法中，通过分析式（1）～（4）可知，各式中等号左边代表t+1 时刻蝠鲼的位置，而等号右边第一项表示t时刻蝠鲼所在位置，其余项之和的含义为t时刻蝠鲼的位移，即速度v（t）。速度作为蝠鲼个体t时刻的移动距离直接与t时刻的位置相加决定蝠鲼t+1 时刻的位置。然而，在离散二进制问题中，解属于｛0，1｝二进制集，对解的每一维参数仅存在“变”和“不变”两种情况，因此应将连续空间中速度的方向性和长短性通过适当的映射表征为二进制空间中的“变”和“不变”两种情况。

本文首先将速度离散为二进制值，然后采用异或算子求解新的位置。首先利用Sigmoid 函数对连续空间中的速度变量进行离散化，设(t)表示t时刻的连续速度变量，则采用SF 法离散速度的步骤如下：

则SF[(t)]为对连续变量(t)二进制离散化后的结果。其中rand（1）表示生成一个服从［0，1］均匀分布的随机数。如果在连续空间中t时刻的速度变量较大则说明t时刻蝠鲼的位置与t+1 时刻的位置相距较远，对应于二进制空间蝠鲼t+1 时刻的位置相对于t时刻则应“变”；反之则应“不变”。因此，t+1 时刻新的位置更新公式如式（7）所示：

其中⊕为异或符号。如果连续空间中t时刻的速度变量较大则由式（6）映射后速度为1 的概率会较大，经式（7）异或运算后(t+1)相对于(t“)变”的概率也较大；反之，则(t+1)相对于(t)“不变”概率较大。因此，本文首先采用式（5）～（6）表示的SF 离散法将连续空间的速度映射到离散的二进制空间，然后再用式（7）所代表的异或算子计算下一时刻的位置。本文提出的DMRFO 中的三个觅食过程分别简述如下：

1）离散链式觅食过程。在MRFO 算法中，速度作为蝠鲼个体当前时刻的位移存在方向性和长短性，但在离散二进制问题中解（位置）属于｛0，1｝二进制集，对解的每一维参数仅存在变和不变两种情况。链式觅食过程中如果当前位置与全局最优位置、前一个体的位置存在较大差异时，速度的绝对值会较大，此时该维参数应该以更大概率向全局最优和前一个体学习，即变；而如果当前位置与全局最优位置、前一个体的位置相同时，速度的绝对值会较小，同时当前位置已为最优的概率较大，此时则应保持不变。因而本文将速度离散为二进制值，并以其和当前位置进行异或求解新的位置。离散链式觅食过程的速度定义如式（8）：

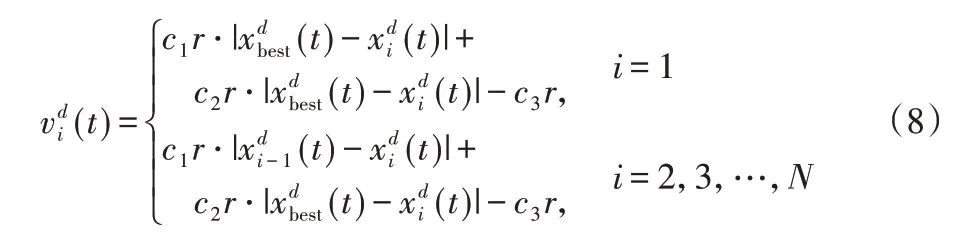
其中c1、c2和c3为权重系数。引入调节因子c3r3是因为如果仅以求差之后的绝对值作为评价当前位置与全局最优的量度（式（8）的前2 项），此时(t)属于闭区间[0，c1+c2]，经由Sigmoid 函数映射后值在0.5 以上，具有不公平性，于是进一步引入调节因子c3r3以保证映射过程取1 和0 的公平性。将式（8）代入式（7）中可得离散化链式觅食的数学模型如式（9）：

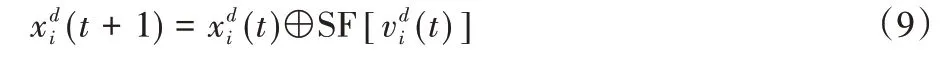
为分析算法的公平性，取数学期望进行分析。当i≥2 时的计算推导过程如式（10）：

为保证映射过程取1 和0 的公平性，则权重系数应满足约束条件：c1=c2，c3=0.5（c1+c2）。当c1=c2=4 时可得不同情况下速度离散概率分析如表1。

由表1 可以看出，当全局最优和前一蝠鲼位置一致，但与当前蝠鲼位置不一致时，(t)的期望值为2、离散为1 的概率为0.88，此时异或出的新位置将以较大概率向全局最优、前一蝠鲼的位置靠近，即相对于当前值变；当前位置、全局最优、前一蝠鲼三者一致时，(t)的期望值为-2、离散为0 的概率为1-0.12=0.88，即异或运算后当前位置以较大概率保持不变；而其他情况下，位置变与不变概率相等。因此，在离散链式觅食过程中，蝠鲼会向全局最优和前一个体学习并根据t时刻速度大小自适应调整t+1 时刻的位置。

表1 链式觅食的速度离散概率分析Tab.1 Discrete probability analysis of velocity in chain foraging

2）离散螺旋觅食过程。在MRFO 算法的螺旋觅食过程中蝠鲼群体在最优解附近进行螺旋运动，以增强对最优解附近空间的开发性能。在离散二进制空间内围绕最优解的螺旋运动过程中，解的每一维参数只有变和不变两种情况。因此以MFRO 算法计算出的连续螺旋觅食速度式（11）作为参考变量采用SF 离散化得到的离散螺旋觅食的数学模型如式（12）所示：

根据认知无线中频谱分配的要求，应使得在最优解附近空间螺旋觅食的搜索结果具有亲1 特性。故取数学期望对离散螺旋觅食过程的亲1 性进行分析，当i≥2，螺旋系数β=4 时，不同情况下速度的离散概率如表2 所示。

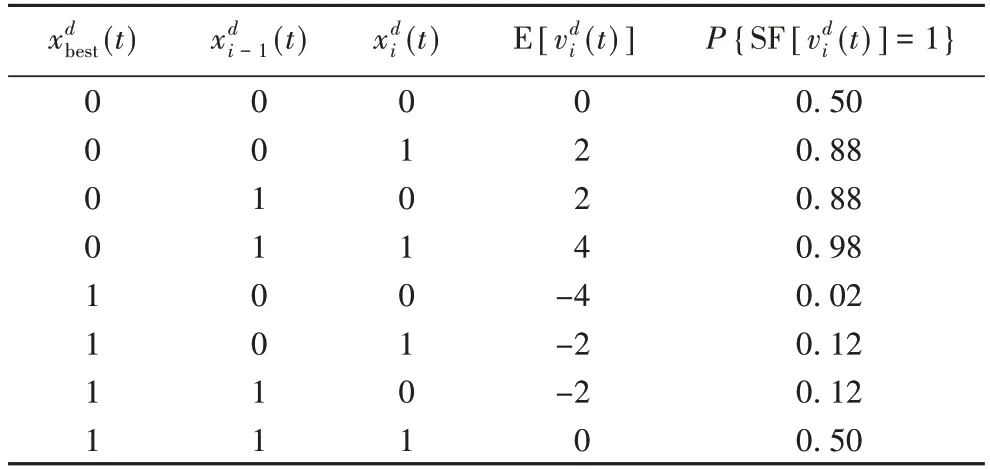
表2 螺旋觅食的速度离散概率分析Tab.2 Discrete probability analysis of velocity in spiral foraging

由表2 可以看出，当全局最优解为0 时，根据频谱分配问题可知其为全局最优的概率较小，故此处设计新解应该以更大的概率变；当全局最优解为1 时，根据频谱分配问题可知其为全局最优的概率较大，故此处设计新解应该以更大的概率不变；其余情况下新解变与不变概率相等。离散化螺旋觅食策略可以使对最优解附近的开发结果以较大概率朝着1的方向改变。离散化螺旋觅食的亲1 特性符合认知无线电中工程实际问题的要求，有利于提升对最优解附近空间的开发，从而避免算法陷入局部最优。

3）离散空翻觅食过程。由于直接采用MRFO 算法中空翻觅食的速度计算式（4）计算出的速度存在长短性和方向性，而二进制问题只存在变与不变，故在离散化时需对之进行二进制的修正，如式（13）。离散空翻觅食过程的数学模型如式（14）：

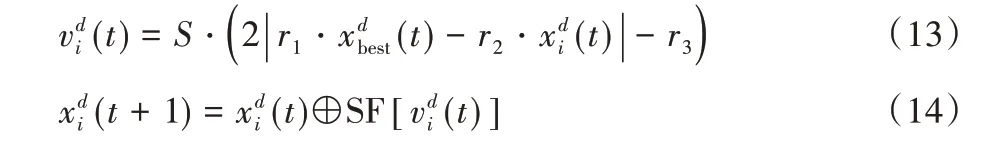
其中：r1、r2和r3分别是服从［0，1］均匀分布的随机数，r3为调节因子；S为空翻系数。引入调节因子是为了保证映射过程取1 和0 的公平性。当S=4 时，离散空翻觅食过程中不同情况下速度离散概率分析如表3 所示。

由表3 可知，当前解和全局最优解不一致时，当前解发生变化的概率为0.88；当前解和全局最优解一致时，当前解变的概率为0.12。该过程可以保证当前解不断向全局最优靠近和学习。

表3 空翻觅食的速度离散概率分析Tab.3 Discrete probability analysis of velocity in somersault foraging

综上所述，在DMRFO 中蝠鲼会向全局最优解和前一个体学习并根据t时刻速度大小自适应调整t+1 时刻的位置。同时，针对认知无线电频谱分配问题的特定背景在离散螺旋觅食过程中引入最优解亲1 性的先验知识，通过在全局最优解附近进行二进制螺旋觅食从而避免算法陷入局部最优以提升算法解决频谱分配问题的性能。此外，为提高算法的可移植性，最优解亲1 性的先验知识仅由螺旋系数β控制。

2 基于DMRFO的频谱分配

2.1 频谱分配模型

在认知无线电网络中，认知用户使用非授权频段的前提条件是不能干扰授权用户的通信，即授权用户有通信请求时认知用户应及时退出该频段。实际通信环境中授权用户、认知用户数量都是不断变化的。如果频谱分配的计算时间相对于通信环境变化可忽略，则在一个较短的时隙内可认为信道参数不变。因此，频谱分配模型可通过频谱可用性矩阵L、效益矩阵B、干扰矩阵C和分配矩阵A描述。假设通信环境中认知用户数量为N，可用频谱数为M，则频谱分配模型的主要参数［5，19-20］可表示为：

1）频谱可用性矩阵：L={ln，m|ln，m∈{0，1}}N×M是一个N×M的二进制矩阵，表征频谱的可用性。即ln，m=1 表示认知用户n可以使用频带m；否则用户n不可使用频带m。

2）效益矩阵：B={bn，m|bn，m∈R+}N×M，其中bn，m是一个正实数，表示认知用户n使用频带m后能带来的网络效益。

3）干扰约束矩阵：C={cn，k，m|cn，k，m∈{0，1}}N×N×M是由M个N×N的二维矩阵组成的三维矩阵，表征认知用户之间的干扰约束情况。其中cn，k，m=1 表示认知用户n和认知用户k同时使用频带m会产生干扰；cn，k，m=1 表示认知用户n、k可同时 使用频带m。显然n=k时，cn，n，m的取值由ln，m决定，即cn，n，m=1-ln，m。

4）分配矩阵：A={an，m|an，m∈{0，1}}N×M是一个N×M的二维矩阵，它代表在某一时隙上M个频带对N个认知用户的无干扰分配策略，其中an，m=1 表示认知用户n在此时隙内使用频带m。显然，分配矩阵必须满足分配时无干扰的条件，即：当cn，k，m=1 时，对∀n，k∈[1，N]，m∈[1，M]，有an，m+ak，m≤1。

基于以上描述，第n个认知用户所能获得的网络效益为

整个通信网络所能获得的网络总效益为

如果设Λ(L，C)N，M表示在给定N、M以及L和C约束情况下的无干扰频谱分配策略集，则频谱分配问题可转化为如下的最优化问题：

2.2 搜索空间压缩

频谱的最终分配策略记录在分配矩阵A中，直接对A进行编码，则搜索空间的维数为N×M，编码维度较高。考虑到A受频谱可用性矩阵L的约束，L中值为0 的元素所对应的A的元素值必定为0，因为不可用频谱必定不能被分配，因此只需将L中值为1 的元素提取出来进行编码，频谱分配完毕后再根据之前的对应关系还原即可。如图1 所示，L为4× 5二维矩阵，缩减为一维矩阵x后，成为一个1× 7 一维矩阵，解x的维数由20 缩减为7，搜索空间由220降为27，极大压缩了搜索空间。

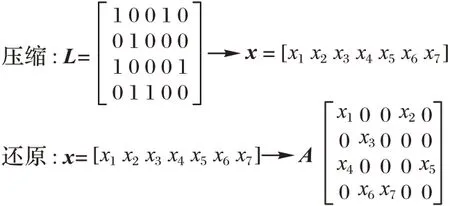
图1 搜索空间压缩与还原实例Fig.1 Example of search space compression and recovery

2.3 基于DMRFO的频谱分配算法流程

搜索空间中，解x的各维参数与A的元素存在一一对应的关系，当x的某一维参数由0 变为1 时，意味着系统尝试将某一信道分配给某个认知用户，如分配满足无干扰分配条件则网络总效益U（β）将会增加由该用户在该信道通信带来的效益值；如分配不满足无干扰分配条件，则系统根据干扰矩阵C随机拒绝当前某一认知用户的通信请求，即将存在干扰的两个参数中的一个随机置0。相反，解x的某一维参数由1变为0 虽不会带来干扰冲突，但却意味着让某个用户退出在某一信道上的通信，此时网络总效益U（β）必定减小，虽尝试了新的解，但却不是朝着网络总效益增大的方向。因此，频谱分配问题的解x具有亲1 特性，DMRFO 算法应引导解朝着由0 向1 的方向搜索。

基于以上描述，首先根据频谱分配模型对实际频谱分配问题进行建模，然后将待分配矩阵A压缩为x，则x张成的二进制空间即为优化算法的搜索空间，基于DMRFO 的频谱分配算法伪码如下所示。

3 仿真实验与结果分析

仿真通信环境的参数L、B、C、M、N设置如下：L为随机生成的0、1 矩阵；B的元素值为从1 到10 间随机选取的实数；C为各二维矩阵随机生成的0、1 二元对称阵；可用频谱数M=22；认知用户数N=20。

3.1 DMRFO算法分析

3.1.1 DMRFO参数比较

本实验旨在验证前文对MRFO 算法离散化过程分析的正确性及所提DMRFO 算法的有效性。在DMFRO 算法中参数c1和c2取值不同会影响觅食行为中的选择概率，因此本实验设定群体规模SN=50，最大迭代次数T=500，进行100 次独立实验观测本文算法的平均收敛情况以研究参数对算法收敛过程的影响。参数c1和c2取不同值时本文算法的收敛结果如图2 所示。

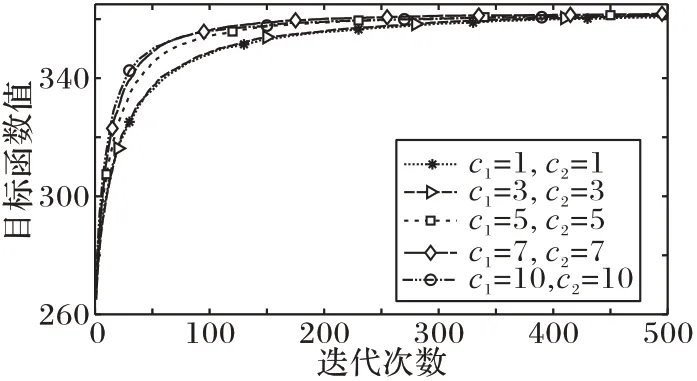
图2 不同参数的算法收敛过程对比Fig.2 Algorithm convergence process comparison of different parameters

通过图2 可知，参数c1和c2的大小会影响DMRFO 算法的收敛速度，但对算法的收敛精度影响较小。因此，综合实验结果和前文的理论分析，在本文后续实验中设定c1=4、c2=4。

3.1.2 DMRFO鲁棒性分析

为分析本文算法在解决频谱分配问题时的鲁棒性，在参数c1=4、c2=4 的情况下，将本文算法（DMRFO）和离散人工蜂群算法（DABC）、二进制粒子群算法（BPSO）以及改进的二进制粒子群算法（IBPSO）分别独立运行100 次以研究算法对随机因素的鲁棒性，实验结果如图3 所示。表4 为不同算法对应的均值和标准差指标值。

综合图3 和表4 可知，本文提出的DMRFO 算法的均值和标准差都优于其他3 个算法。均值反映了算法收敛精度的优劣，而标准差反映了收敛结果的稳定性。因此，本文算法在收敛性能上优于DABC、BPSO 和IBPSO 算法。

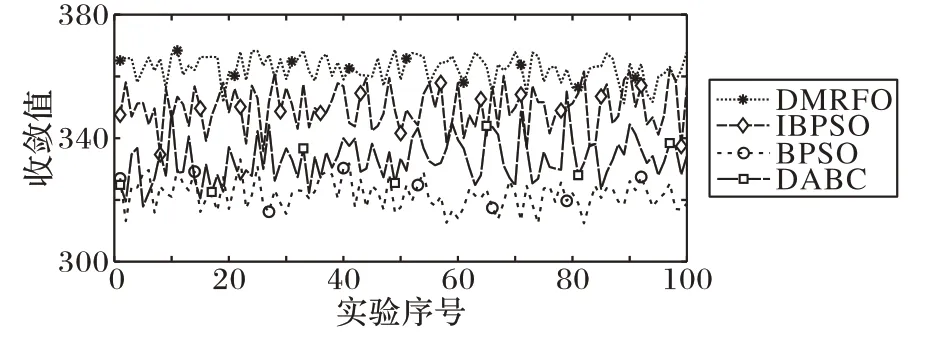
图3 不同算法的鲁棒性对比Fig.3 Robustness comparison of different algorithms

表4 不同算法的均值和标准差Tab.4 Mean and standard deviation of different algorithms

3.2 网络总效益比较

3.2.1 最大网络效益仿真

频谱分配基于某一瞬间信道环境不变的假设，以最大化网络效益为目标函数，故要求算法能够快速高效地收敛。本文对DMRFO 算法和DABC、BPSO、IBPSO 等典型算法在相同信道环境下进行对比，分别独立重复30 次实验后得到的平均网络总效益收敛曲线如图4。

图4 不同算法的网络总效益收敛曲线Fig.4 Convergence curves of network total benefit of different algorithms

由图4 可知，DMFRO 的收敛结果远优于DABC、BPSO 和IBPSO 算法。该实验说明相比经典的算法，本文提出的DMRFO 算法更适合解决频谱分配问题。这是因为首先MFRO 的机制本身要优于DABC 和BPSO，其次通过设计离散化策略将频谱分配问题的先验性信息有效融入到了DMFRO算法的运行机制中。

3.2.2 不同环境下网络总效益仿真

为验证本文算法的普遍性，分别采用本文算法对30 种不同的通信环境进行频谱分配仿真实验，不同通信环境下获得的最大网络总效益及和其他典型算法的对比如图5所示。

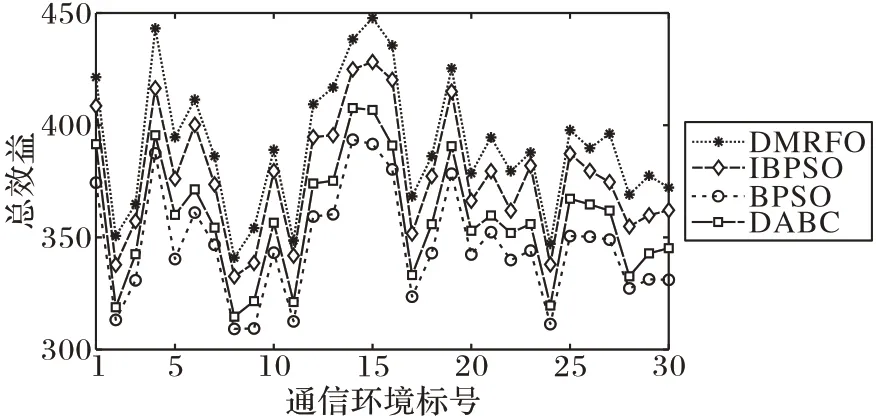
图5 不同通信环境下不同算法的网络总效益Fig.5 Network total benefits of different algorithms in different communication environments

由图5 可知，随着通信环境不同，认知用户使用空闲信道的频谱后能带来的网络总效益也不同，但本文算法所带来的网络总效益始终大于DABC、BPSO 和IBPSO 算法获得的网络总效益。因此，本文提出的DMRFO 算法具有更好的频谱分配性能。

3.3 用户平均效益

3.3.1 不同用户数下的平均效益

设环境中可用频谱数M=22 保持不变，当认知用户数N不断增加时，认知用户的平均效益随认知用户数的变化曲线如图6 所示，可以看出，随着认知用户数不断增加，单个认知用户能获得的平均效益呈递减变化。

由图6 可知，在认知用户数较少时，即频谱资源充足，四种频谱分配算法的结果相近；但当认知用户数较多时，即频谱资源比较紧缺，本文算法的分配结果显著优于其他三种经典算法。

图6 认知用户数N递增时的平均效益Fig.6 Average benefit with the number of cognitive users N increasing

3.3.2 不同信道数下的平均效益

设认知用户数N=20 不变，当可用频谱数M不断增加时，单个认知用户获得的平均效益值曲线如图7 所示，随着可用频谱数的增加，单个用户获得的平均效益值不断增加，且DMRFO 算法显著优于其他3 种算法。

随着通信环境中可用频谱数M增加，频谱分配问题的求解规模越大。从图7 可知，当求解问题的规模较小时，4 种算法都能取得最优结果，但随着求解问题规模递增，DMRFO 算法的性能显著优于其他3 种典型算法。

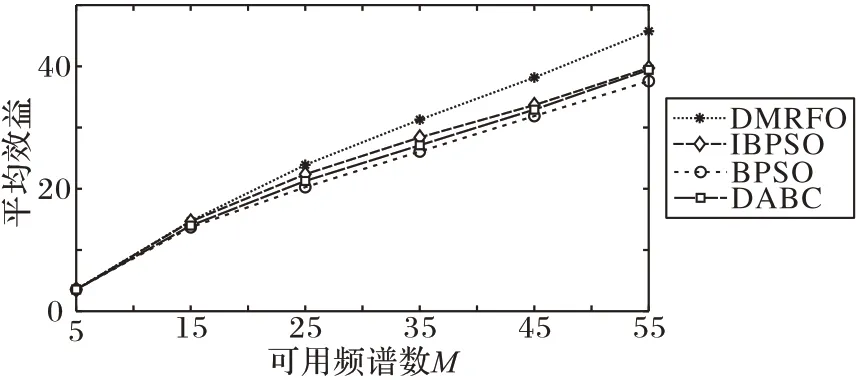
图7 可用频谱数M递增时的平均效益Fig.7 Average benefit with the number of available spectrums M increasing

综上所述，本文提出的基于DMRFO 的频谱分配算法显著优于典型的DABC、BPSO 和IBPSO 频谱分配算法。

4 结语

针对MRFO 算法只能处理连续函数的优化问题而不能解决频谱分配问题的不足，本文提出了DMRFO 算法，然后将该算法应用于解决认知无线电中的频谱分配问题。本文的主要工作如下：

1）通过SF 离散法和异或算子使蝠鲼可以根据当前时刻速度大小自适应调整下一时刻的位置从而向全局最优解和前一个体学习。同时，针对认知无线电频谱分配问题的特定背景，在离散螺旋觅食过程中引入最优解亲1 性的先验知识，通过在全局最优解附近进行二进制螺旋觅食从而避免算法陷入局部最优，以提升算法解决频谱分配问题的性能。此外，为提高算法的可移植性，最优解亲1 性的先验知识仅由螺旋系数β控制，从而方便了先验性知识的引入和删除。

2）将本文提出的离散蝠鲼觅食优化算法用于解决认知无线电中的频谱分配问题，显著提升了网络的效益，取得了较好的效果。