利用初始残差和解耦操作的自适应深层图卷积

张继杰，杨 艳，2*，刘 勇，2

（1.黑龙江大学计算机科学技术学院，哈尔滨 150080；2.黑龙江省数据库与并行计算重点实验室（黑龙江大学），哈尔滨 150080）

0 引言

图在真实世界中无处不在，其在建模结构化和关系型数据的过程中发挥了关键的作用，如社交网络［1-2］、知识图谱［3］和化学分子［4］。人们想要将卷积神经网络应用到不规则的图结构上，在这种需求的驱使下，Kipf 等［5］首次提出了图卷积网络（Graph Convolutional Network，GCN）。在图卷积网络被提出后不久，Veličković 等［6］提出了图注意力神经网络（Graph ATtention network，GAT）。

GCN 和GAT 经常被用来对图中的节点进行分类，节点分类是网络表示学习［7］领域一项重要的任务。例如，在引文网络中，对每个论文节点的领域和主题进行预测，就是一个最常用的节点分类任务。目前，图神经网络在这一任务上取得了巨大的成功，成为解决这一问题的有效手段。图神经网络通过迭代地整合节点的邻居表示，生成有效的节点表示。然而，像GCN、GAT 这些模型都在两层时效果达到最佳，这种浅层的体系结构限制了它们从高阶邻居中提取信息的能力。堆叠更多的层数和增加非线性往往会降低这些模型的性能。造成这种情况的主要原因可以归结为过拟合和过平滑，前者是随着层数的不断加深，模型的参数不断增多，模型的训练难度不断提升，导致模型性能下降。对于后者而言，Li 等［8］首次指出图卷积网络的每一层就是一种特别的拉普拉斯平滑。简单来讲，拉普拉斯平滑就是让一个节点和它周围的节点尽可能相似，每个节点的新特征是其周围节点特征的均值，进行多次图卷积会导致连通图中的节点趋近于相同的值，使得图中不同类别的节点不可区分。对于所含信息较少的图来说，利用节点的高阶邻居信息是必不可少的，因此缓解过平滑问题是很有必要的。

为了进一步缓解过平滑问题，本文提出了基于图卷积结构的模型，将图卷积中原本耦合在一起的表示转换和特征传播操作进行了解耦。在原始的图卷积传播过程中需要一个转换矩阵，因此当考虑到大的接受域，即堆叠多层图卷积时，模型的参数量会非常多，很难用大量的参数来训练一个多层图卷积神经网络模型。其次，在基于图中连接的节点属于同一类的假设下，特征传播只是简化了分类任务，让连接的节点的表征更相似。相关研究证明，仅用多层感知机（Multi-Layer Perceptron，MLP）对节点初始表示进行降维并分类，效果表现较差。综上分析，本文模型首先将节点的原始特征通过多层感知机生成用于之后传播的表征，然后在特征传播过程中加入了初始残差。在得到不同传播层的节点表征之后，本文模型利用自适应机制将不同传播层的节点表示进行加权求和生成最终用于分类的节点表示。本文的模型在常用的引文数据集上取得了相较经典的基线模型更优的效果，且在缓解过平滑方面有着显著的效果。

综上所述，本文的主要工作如下：

1）将初始残差和解耦操作共同应用到图卷积网络中，并通过自适应机制得到最终的节点表示。

2）实验结果表明，本文模型的节点分类准确率优于多个基线系统，同时能更好地缓解过平滑。

1 相关工作

1.1 残差连接

残差网络（Residual Network，ResNet）［9］等深层卷积神经网络的出现，为图像分类任务带来了效果的巨大提升，于是后续有很多工作将残差连接应用到深层图卷积当中来缓解过平滑问题。

节点自身的信息在深层的图卷积传播过程中丢失，使得最终的节点表示不具备原始特征信息。很显然，通过残差连接，节点的浅层特征信息将会在图卷积传播过程中一直保留下来。

将图卷积网络与个性化的网页排序（Page Ranking，PageRank）算法［10］联系在一起，通过在PageRank 的随机游走中保留部分根节点信息来改进模型，随后得到了个性化的PageRank 模型。然后，Klicpera 等［11］将这种传播方式移植到图卷积网络中，得到利用初始残差进行传播的图卷积神经网络 APPNP（Approximated Personalized Propagation Neural Predications）。Cluster-GCN（Cluster Graph Convolutional Network）［12］提出残差连接要考虑图卷积网络层数的影响，简而言之就是节点对离得近的邻居的影响力应该更大。GCNII（Graph Convolutional Networks via Initial residual and Identity mapping）［13］则是通过将初始残差和恒等映射这两个简单的技术应用到了图卷积网络中来获取更好的效果。

1.2 归一化隐表示

目前有工作将BatchNorm（Batch Normalization）技术［14］迁移到了图卷积网络中，PairNorm（Pair Normalization）［15］将每一层图卷积的输出进行正则化，并保持总的节点对的相互距离不变，这样随着图卷积的进行，图中连接的节点距离减少，相应地没有连接的节点之间的距离会被拉大。

1.3 将图稀疏化

DropEdge（Dropout Edge）［16］就是dropout［17］在图神经网络上的扩展。在训练过程中，dropout 会随机删除一些输入数据的特征，而DropEdge 则随机删除邻接矩阵中的一些边。假设图的邻接矩阵有P条边，随机选取固定数量的边进行删除，然后用剩余的邻接矩阵代替原来的邻接矩阵输入到图卷积网络中进行训练，当图卷积网络有多层时，每层删除的边可以不一样。GRAND（Graph RAndom Neural Networks）［18］提出随机传播策略进行数据增强，其中应用的DropNode（Dropout Node）就是将图稀疏化的一种策略。

1.4 解耦图神经网络

DAGNN（Deeper Adaptive Graph Neural Networks）［19］分析了图卷积网络中表示转换和特征传播的耦合会促使深层图卷积性能下降。因此，将这两个操作进行了解耦并自适应地整合不同传播层的表征，在一定程度上缓解了过平滑问题。

上述四种方法虽然都在缓解过平滑上取得了一定的效果，但是每种方法并没有考虑与其他方法是否可以联系在一起来缓解过平滑问题，本文就是将残差连接和解耦操作进行了联系，从而进一步缓解过平滑。

2 问题定义

2.1 过平滑

图卷积可以被认为是一种特殊形式的拉普拉斯平滑。简单讲，拉普拉斯平滑就是让一个节点和它周围的节点尽可能相似，每个节点的新特征是其周围节点特征的均值。虽然拉普拉斯平滑的特性给图卷积带来了很多好处，使得每个节点能够更好地利用周围节点的信息，但它也带来了对图卷积模型的限制。研究者发现，叠加越来越多的图卷积网络层后，结果不仅没有变得更好，反而变差了，效果变差是因为连通图中的节点表示趋近于相同的值，这就是所谓的过平滑问题。

2.2 变量及其含义

为了更好地描述本文模型，表1 给出了主要符号及其含义。

表1 符号及其含义Tab.1 Symbols and their definition

2.3 相关定义

本节给出了本文用到的一些定义。

定义1无权无向图。给定一个拥有N=|V|个节点和M=|E|条边的图G=(V，E)，其中节点集V={v1，v2，…，vN}，边集E={e1，e2，…，eM}，图中的边没有被赋予权重（默认为1）且无向。

定义2邻接矩阵和度矩阵。相应的A∈{0，1}N×N代表图的邻接矩阵，邻接矩阵的第i行、第j列的元素表示为Ai，j，如果节点vi和节点vj存在连接关系，则Ai，j=1，否则Ai，j=0。I代表主对角线全为1 的单位矩阵，=A+I代表添加自环之后的邻接矩阵。由于图是无向的，不论是否添加自环，其邻接矩阵都是对称的，即Ai，j=Aj，i。D代表度矩阵，di是度矩阵D的对角元素，di=。代表加自环的度矩阵。

定义3网络表示学习。给定图G=(V，E)和初始的节点特征矩阵X∈RN×d，节点vi对应一个d维的向量Xi。网络表示学习的目标是学习映射函数f：X∈RN×d→Z∈RN×c，将图G中的每一个节点映射成c维的向量，满足c≪d，得到的节点表示矩阵Z∈RN×c用于预测节点的类别。

定义4半监督学习。半监督学习介于传统监督学习和无监督学习之间，其思想是在标记样本数量较少的情况下，通过在模型训练中直接引入无标记样本，以充分捕捉数据整体潜在分布，以改善如传统无监督学习过程盲目性、监督学习在训练样本不足导致的学习效果不佳的问题。

3 本文模型

3.1 模型描述

本节将首先给出两层图卷积的原始公式，如式（1）所示：

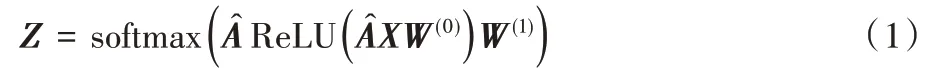
式（1）可以看出，图卷积过程中，特征传播和特征转换是耦合在一起的，这使得当进行深层的图卷积时，模型的训练难度变大。SGC（Simplifying Graph Convolutional networks）［20］提出将图卷积中的转换矩阵去除，只在最后一层添加转换矩阵，在性能提升很大的同时与图卷积网络产生了具有竞争力的分类效果。其性能提升很大一部分原因是去除了大量的训练参数，使得模型简化；但它仍避免不了随着层次的加深出现过平滑现象。

本文提出了一种网络表示学习模型ID-AGCN（using Initial residual and Decoupled Adaptive Graph Convolutional Network），以图卷积神经网络为基础，去除了非线性激活函数和转换矩阵，沿用了之前介绍的残差连接和解耦操作，并且利用了自适应机制来得到最终的节点表示。

为了解耦图卷积中的特征传播和表示转换，本文提出的模型先利用多层感知机处理节点的原始表示，以便生成用于之后传播的表示。这些表示只含有节点本身的信息，不包含结构信息，而且维度要比节点初始的特征维度小很多，这里用第i个节点进行举例，如式（2）所示：

其中：是经过多层感知机降维得到的节点表示，c≪d。图的结构信息会在传播过程中被整合到节点表示中，随着传播的层数逐渐增大，节点本身的信息占比会逐渐减小。为了进一步保留节点本身信息，本文方法是在传播过程中利用了初始残差连接，这样即使传播很多层，生成的节点表示仍能保留部分节点本身信息，如式（3）、（4）所示：

其中是节点vi经过ℓ 层传播得到的表示。

然而很难确定一个合适的层数进行传播。过少的层数将不能获取足够和必要的邻居信息，过多的层数将会带来过多的全局信息从而消除了具体的局部信息。每个节点理想中最合适的接受域是不同的，不同的传播层得到的表征对节点最终的表征具有不同的影响程度。为了解决这一问题，本文采用了一个可学习向量ui∈Rc与不同传播层得到的节点表示进行计算，得到相应表示的保留分数。这些保留分数衡量了由不同传播层产生的相应表示的信息量有多少应予以保留，如式（5）所示：

其中uℓ是经过ℓ 层图卷积得到的表示的保留分数。

然后将来自不同传播层的表示进行加权求和得到最终的节点表示，如式（6）所示：

其中zi是节点vi的用于预测的最终表示。

利用这种自适应的调整机制，模型可以做到自适应地平衡每个节点的局部和全局邻域的信息。

本文模型的整体框架如图1 所示。

图1 本文模型框架Fig.1 Framework of the proposed model

3.2 模型的矩阵运算

3.1 节介绍了单个节点的更新方式，这里采用矩阵运算来方便多个节点的更新。

这里的H0是初始的节点表示矩阵X经过多层感知机之后得到的用于传播的表示矩阵。

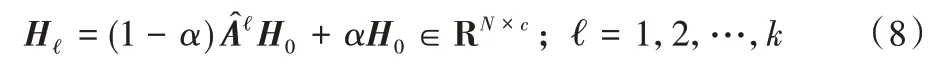
其中Hℓ是节点在第ℓ 层的表示矩阵。

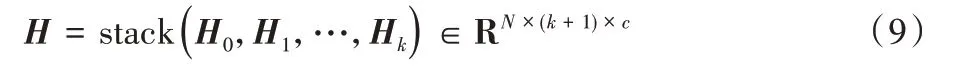
将不同传播层得到的表示矩阵利用stack 操作进行堆叠来得到表示矩阵H，将此表示矩阵用于后续保留分数的计算。

利用一个共享可学习的向量u∈Rc×1来计算不同传播层表示的保留分数，得到保留分数矩阵U。

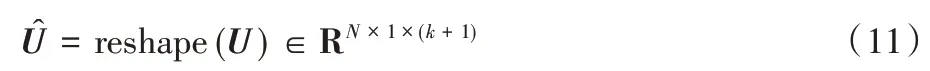
利用reshape 操作将保留分数矩阵U进行维度变换得到U^。

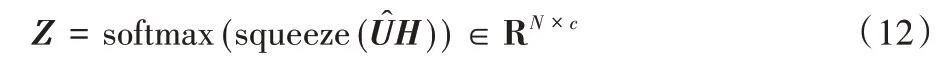
利用squeeze 进行维度压缩，用softmax 进行归一化操作，得到用于预测的节点的表示矩阵Z。

3.3 构建损失函数

本文任务为半监督的节点分类［21］，利用图中部分带标签的节点构造监督损失函数。假设n个节点中有m个带标签的节点，那么构造的交叉熵损失函数如式（13）所示：

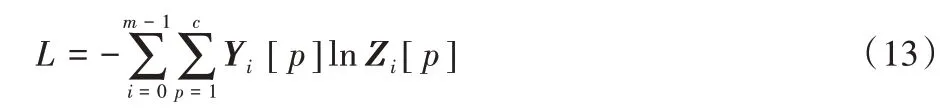
其中：Yi指的是节点vi的真实标签，Zi表示节点vi的预测表示，Zi第p维的数值代表节点属于第p类的概率。

3.4 算法流程

本文所提的ID-AGCN 如算法1 所示。

算法1 ID-AGCN。

输入 无权无向图G=(V，E)，对称归一化的邻接矩阵，节点特征矩阵X∈RN×d，图卷积层数k，初始残差保留率α，节点类别数c，多层感知机fmlp(X，θ1)，可学习的向量u∈θ2。

4 实验与结果分析

4.1 数据集

本文选取了3 个公开真实的引文数据集进行实验验证，其统计数据如表2 所示。

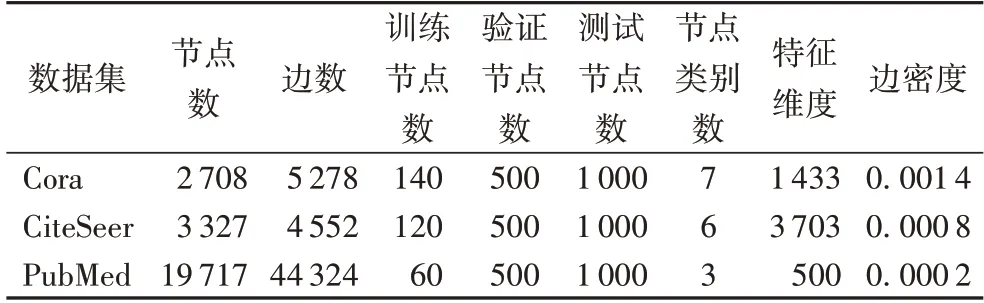
表2 引文数据集Tab.2 Citation datasets

这3 个引文数据集中的每一个节点代表一篇论文，它们之间的连边代表引用关系。Cora 数据集中有2 708 篇论文，共存在5 429 条边，类别数为7，代表这些论文共分为7 个研究领域，每篇论文都由一个1 433 维的向量来表示。CiteSeer数据集共有3 327 篇论文，类别数为6，每篇论文由一个3 703维的向量表示。PubMed 数据集共有19 717 篇论文，类别数为3，每篇论文由一个500 维的向量表示。数据集的分割采用了文献［22］中的分割方法，训练集是从每一类中取20 个节点进行训练，用500 个节点验证，用1 000 个节点测试。

此外，本文还计算了3 个数据集的边密度，计算结果显示，PubMed 数据集最为稀疏。其中，边密度ρ的计算公式如下：

其中：m表示边数，n表示节点数。

4.2 实验环境与模型对比

本文的实验环境为AMD Ryzen 7 5800H，CPU@3.20 GHz，16 GB 内存，Windows 10 64 位操作系统，8 GB 显存的NVIDIA GeForce RTX 3070。使用Pytorch 和Pytorch Geometric 实现本文模型以及相应的基线模型。

ChebNet（Chebyshev Network）［23］：一种实现快速局部化和低复杂度的谱域图神经网络，由于使用了切比雪夫多项式展开近似，所以这个网络又称切比雪夫网络。

GCN［5］：在切比雪夫网络的基础上，将切比雪夫网络中的多项式卷积核限定为1 阶，极大减少了计算量。

GAT［6］：在为图中每个节点计算向量表示时，利用注意力机制加权节点的邻居，可以跨节点并行计算。

SGC［20］：在多层图卷积网络中，去除每一层的非线性函数，多层图卷积网络叠加之后的简化模型仍然可以看作两部分，左边是多层图卷积，右边是多个全连接线性层，叠加多层之后的图卷积仍然起到了低通滤波的作用，并将多个全连接线性层合并到一起。

APPNP［11］：利用了初始残差进行图卷积传播，只有最开始计算降维的节点向量表示时引入了参数，接下来的更新步骤都是无参数的，使得增加层数不会对整个图神经网络的参数量造成影响，因此只需要很少的参数就可以传播到更多的层，而不容易造成过平滑问题。

DAGNN［19］：将图卷积网络中的表示转换与特征传播进行了解耦，并且采用了自适应机制进行了节点向量表示整合，没有应用残差技术。

本文利用不同的模型对3 个引文数据集进行了半监督的节点分类准确率对比，对每个模型进行了100 次的实验，统计数据如表3 所示。

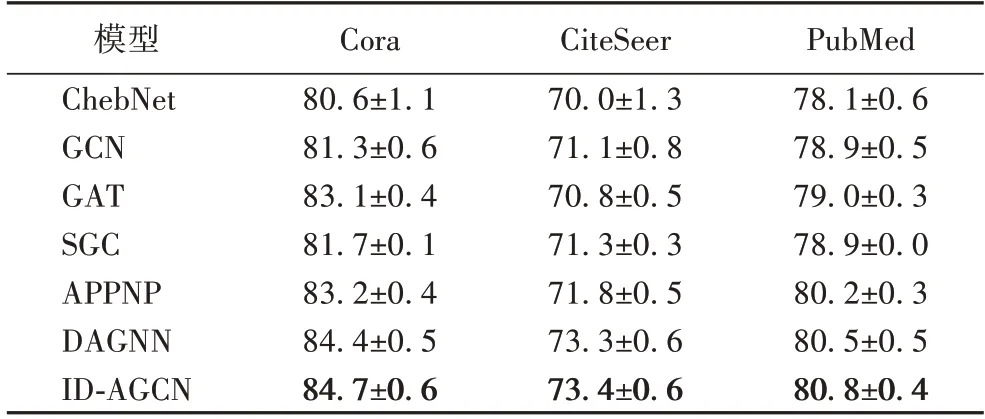
表3 引文数据集分类准确率结果 单位：%Tab.3 Classification accuracy results for citation datasets unit：%

从表3 可以观察到，ID-AGCN 在这3 个数据集上的分类效果相较GCN 分别提升了3.4、2.3 和1.9 个百分点，表明了本文模型在引文数据集半监督节点分类任务上的优越性。

4.3 模型参数设置

为了寻找本文模型的最佳参数，模型参数的搜索范围为：

1）k∈{5，10，15，20，25，30，35，40}；

2）weight decay ∈{0，0.005，0.01，0.015，0.02}；

3）α∈{0.01，0.02，0.03，0.04，0.05，0.1，0.15，0.2}；

4）dropout rate ∈{0.5，0.55，0.8，0.85}；

5）学习率固定为0.01。

经过网格搜索，模型的最优参数设置如表4 所示。

表4 参数设置Tab.4 Parameter setting

4.4 过平滑实验分析

由于像GCN、GAT 这种模型是浅层的图神经网络模型，不适合进行缓解过平滑实验对比。为了验证模型在缓解过平滑方面的能力，首先规定图卷积层数k分别为5、10、15、20、50、100、200 和300，然后采用简化的图卷积模型SGC、深层图卷积模型DAGNN 与本文模型在Cora 数据集上进行实验对比，如图2 所示。

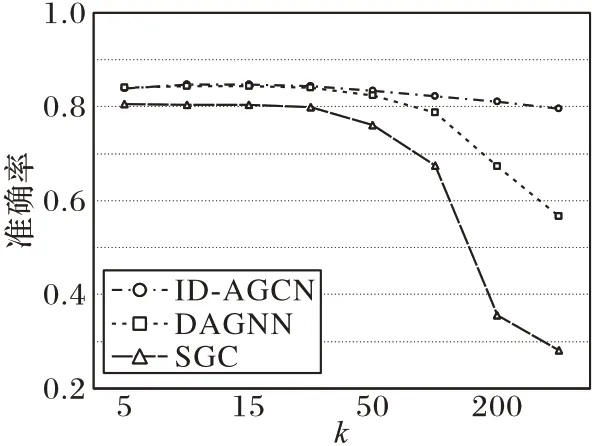
图2 缓解过平滑结果对比Fig.2 Comparison of over-smoothing alleviation results

从图2 中可以看出，随着图卷积层数的加深，本文提出的模型相较SGC 和DAGNN 有更好的缓解过平滑能力，表明了本文模型在缓解过平滑方面的有效性。

4.5 模型运行时间对比

本文在各模型达到最优效果的前提下，在Cora 数据集上进行运行时间的对比，统计数据如表5 所示。

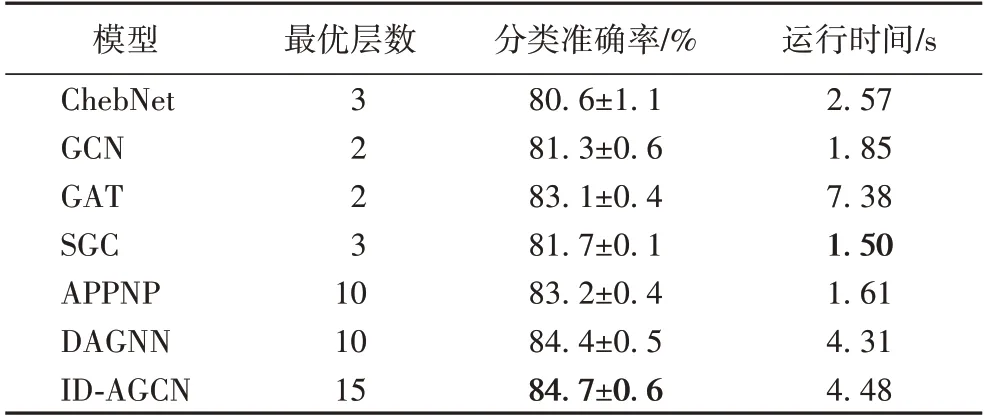
表5 不同模型分类准确率和运行时间对比Tab.5 Classification accuracy and running time comparison of different models

通过表5 看出，简化之后的图卷积模型SGC 在运行时间上占优，但是其分类准确率相较本文模型少了3 个百分点。因为本文模型是深层图卷积，其层数肯定多于简化的图卷积模型，运行时间也会增多，但分类效果提升明显。

4.6 消融实验

本节主要进行模型关键模块的消融，模型的关键模块包括初始残差连接和自适应机制，将初始残差连接称为IR（Initial Residual），将自适应机制称为AM（Adaptive Mechanism），将去除操作用w/o 表示，通过消除不同的模块来进行实验对比。值得一提的是，去掉自适应机制指的是将来自不同传播层的节点表示进行平均聚合。图卷积层数k遵从前文的设定，分别为5、10、15、20、50、100、200 和300，在Cora 数据集上进行了模型消融对比，实验结果如图3 所示。

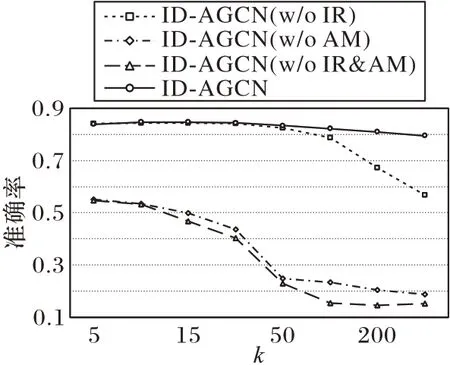
图3 消融实验结果对比Fig.3 Result comparison of ablation experiments

4.7 参数敏感性分析

本节研究模型对其主要参数的敏感性，主要包括残差保留率α和图卷积层数k。

本文在3 个引文数据集上对这两个参数进行了分析，实验设置残差保留率α分别为0.05、0.1、0.15 和0.2，图卷积层数k分别为5、10、15、20、50、100、200 和300 来研究它们对模型性能的影响，图4 和图5 记录了模型准确率在3 个数据集上针对不同参数的变化。

图4 参数α的影响Fig.4 Influence of parameter α

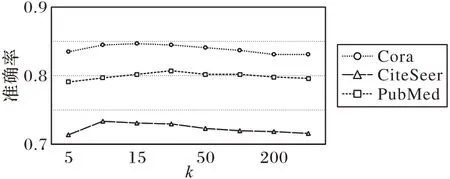
图5 参数k的影响Fig.5 Influence of parameter k

从图4 可以看出，随着残差保留率α的逐渐增大，模型的性能有些许下降，表明在进行深层图卷积时不宜加入过多的初始特征信息。从图5 可以看出，随着图卷积层数k的增多，模型的性能会下降，这是不可避免地产生了过平滑问题，但是本文模型在缓解过平滑方面的能力是较好的，即使在层数为300 时，节点的分类准确率依旧很高，表明了本模型缓解过平滑的有效性。

4.8 可视化

本节利用t-SNE（t-distributed Stochastic Neighbor Embedding）技术对Cora 数据集中1 000 个测试的节点进行可视化，t-SNE 是机器学习中用于降维的一种算法，它基于多维缩放和等距特征映射更改了距离不变性的概念，并在将高维映射到低维的同时确保了它们之间的分布概率不变，具体的结果如图6 所示。

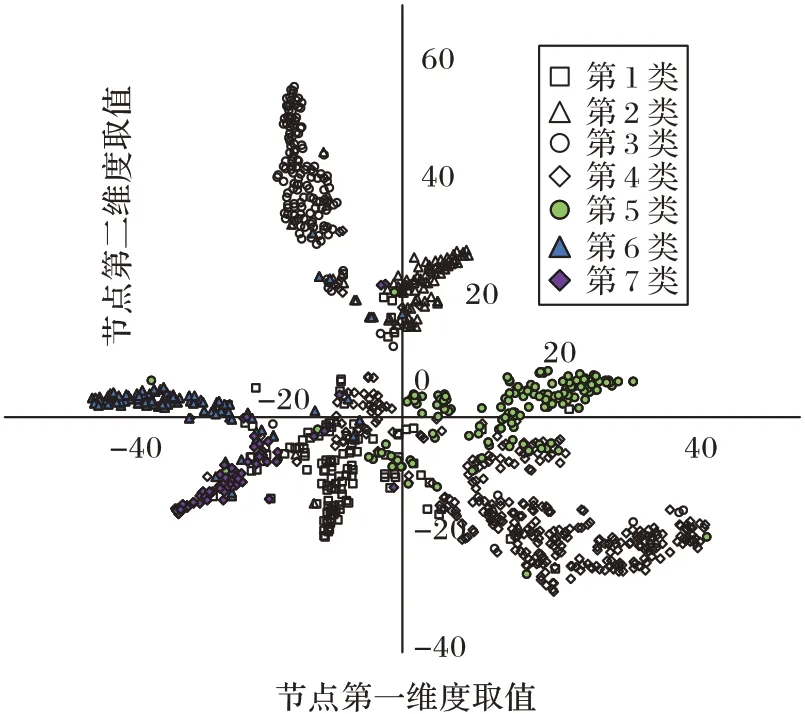
图6 Cora数据集可视化结果Fig.6 Cora dataset visualization results

1 000 个测试的节点总共分为7 个类别，从图6 中可以看出，本文模型对于节点分类这一任务有较好的效果。

5 结语

本文提出了一种缓解深层图卷积网络过平滑的模型，该模型主要采用初始残差连接以及解耦图卷积网络改进原始的图卷积，并利用自适应机制整合不同传播层的节点表征。在3 个真实公开的引文数据集上的实验结果表明了本文模型的有效性。

本文模型主要做的是半监督且直推式的节点分类任务，其局限是不能扩展到其他图上，即使是在同一个图上，要测试的点如果不在训练时就加入图结构，本文模型是没有办法得到它的嵌入表示的。但实际应用中往往需要通过学习已知数据的规律泛化到未知的数据上，因此以后可以考虑改进本文模型，进行一些归纳式的预测任务。