基于随机特征映射的四层多核学习方法

杨 悦，王士同

（江南大学人工智能与计算机学院，江苏无锡 214122）

0 引言

核方法（kernel methods）［1-3］是以支持向量机（Support Vector Machine，SVM）［4-6］为典型代表的一类机器学习算法，因引入核函数解决非线性问题而得名。对于原始输入空间中混叠、线性不可分的数据，首先采用某个非线性函数将其映射到高维甚至无穷维的特征空间，然后在此特征空间中应用模式分析方法，如分类、聚类、回归、降维等。在网络模型给定核函数后，数据在特征空间中的分布结构随即确定。这意味着，核方法的性能好坏很大程度上取决于所选用的核函数的性能。不同类型或同类型但参数取值不同的核函数，都会造成不同的网络性能。

近几年Huang 等［7］提出的极限学习机（Extreme Learning Machine，ELM）和Chen 等［8］提出的宽度学习（Broad Learning System，BLS）算法都是基于单个特征空间的单核神经网络，算法核心思想在于随机选取网络的输入权值和偏置，在训练过程中保持不变，仅需要优化隐层神经元个数。网络的输出权值则是通过求解Moore-Penrose 广义逆运算得到。相较于其他传统的前馈神经网络学习算法，这种训练方法具有实现简单、学习速度极快和人为干预较少等显著优势。为了保持网络在训练速度上的优势，并且优化算法的结构，文献［9］中提出了基于随机映射特征的四层神经网络（Four-layer Neural Network based on Randomly Feature Mapping，FRMFNN）模型。首先把原始输入特征通过特定的随机映射算法转化为随机映射特征存储于第一层隐藏层节点中，再经过激活函数对随机映射特征进行非线性转化，生成第二层隐藏节点，最后将第二层隐藏层通过输出权重连接到输出层。由于第一层和第二层隐藏层的权重是根据任意连续采样分布概率随机生成的，不需要训练更新，且输出层的权重可以用岭回归算法［10］快速求解，从而避免了传统反向传播神经网络耗时的训练过程。尽管上述的方法模型在众多的应用领域有效并且实用，但这些方法都是基于单个特征空间的单核方法。由于在不同的应用场合，不同核函数的性能表现差别很大，所以核方法的性能优劣很大程度上取决于所选用的核函数及其参数，而核函数的构造或选择至今没有完善的理论依据。此外，当样本数据含有异构信息、样本规模很大、多维数据不规则或数据在高维特征空间分布不平坦的情况［11-14］下，采用单个简单核函数进行映射的方式对所有样本进行处理的效果并不理想。针对这些问题，近年来，出现了大量关于核组合方法的研究，即多核学习方法［15］。多核学习的目标就是将多个子核（或称为基核）通过线性组合或非线性组合的学习方法得到一个多核矩阵，其实质就是学习多个核函数的最优凸组合［16］，得到这些特征所形成的单一核的权系数，从而组合成一个多核函数。对于多核学习的优化问题，许多学者做了研究。文献［17］中针对多核学习算法时间复杂度随内核数量增加而大幅增长的问题，提出了一种可拓展的多核学习算法：easyMKL（easy Multiple Kernel Learning），可以高效处理成千上万甚至更多的核函数；文献［18］中提出一种名为SimpleMKL 的算法，通过加权L2正则化公式解决了多核学习算法需要大量迭代才能收敛的问题，并在权重上附加了约束项以得到稀疏核组合；文献［19］中提出的GMKL（more Generality Multiple Kernel Learning）在保证现有大规模数据集优化算法的效率的同时，将现有的多核学习算法公式进行拓展来学习受一般正则化约束的一般核组合；文献［20］在回归和核岭回归算法的基础上研究了基于基本核的多项式的优化问题，提出了一种非线性多核学习算法（Non-Linear Multiple Kernel Learning，NLMKL），用一种更简单的极小值问题来简化优化过程中的极大极小值问题，并给出了一种基于投影的梯度下降算法来解决该优化问题；文献［21］基于group-Lasso 和多核学习间的等价关系，提出了GLMKL（Group Lasso Multiple Kernel Learning）算法，制定了用于优化核矩阵权重的封闭形式解决方案以提高多核学习的效率，并且该方法可以推广到Lp（p≥1）范数的多核学习的情况。

文献［9］中提出的FRMFNN 模型虽然具有很好的泛化能力，但是存在隐藏层节点规模较大的问题。针对这个问题，本文提出一种基于随机特征映射的四层多核学习神经网络（Four-layer Multiple Kernel Neural Network based on Randomly Feature Mapping，MK-FRMFNN），对原始的数据特征根据任意连续采样分布概率进行不同的随机映射，生成随机映射特征，并使用嵌入式选择的方式对特征进行稀疏化处理，再通过不同的核函数对这些随机映射特征的稀疏化特征进行非线性随机映射，最后把不同的基本核矩阵通过线性组合的方式连接到输出层，通过岭回归算法计算出网络的输出权重。通过多核组合学习的方式，在保证网络泛化性能的同时，可以大大降低网络的隐藏层节点规模。而对于样本规模较大的数据集，传统的多核算法在核映射过程中会造成严重的“维数灾难”问题。与传统的多核学习不同，MK-FRMFNN 模型通过随机核映射的方式，调节随机权重矩阵的维度来控制核空间的维度，有效解决了大样本数据集的维数灾难问题。本文具体描述了随机映射特征的核组合学习算法及其相关概念；对网络进行正则化处理，并给出了两种不同的核组合方式：基于局部特征的核组合和基于全部特征的核组合；最后，在多个分类数据集上的实验表明，MK-FRMFNN 多核模型有效降低了网络隐藏层的节点规模，并且具有良好的分类能力及泛化性能。

1 相关工作

1.1 核方法

核方法的使用可以有效提高支持向量机一类的算法对于线性不可分数据的处理能力。下面以经典的支持向量机为例阐述核函数的推导过程。设原始样本向量为x，通过一个映射函数Φ(x)映射到高维特征空间，则SVM 的目标函数形式转换为：

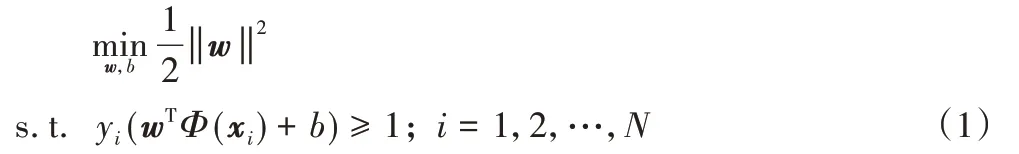
引入拉格朗日乘子后得到的对偶问题为：

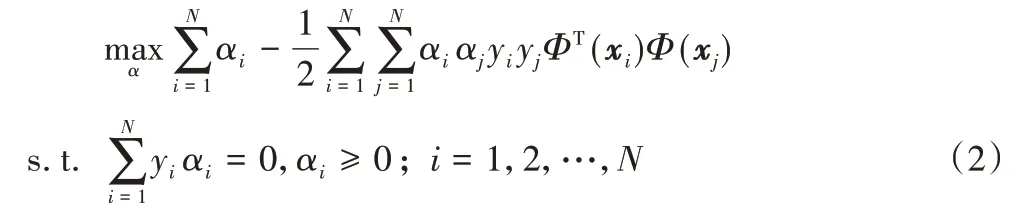
由于样本映射到高维特征空间后，样本维度可能是无穷的，故ΦT(xi)Φ(xj)的直接计算较为困难，此处可假设有函数κ(·，·)使κ(xi，xj)=ΦT(xi)Φ(xj)，则对式（2）求解后可得到对未知样本的判别函数：

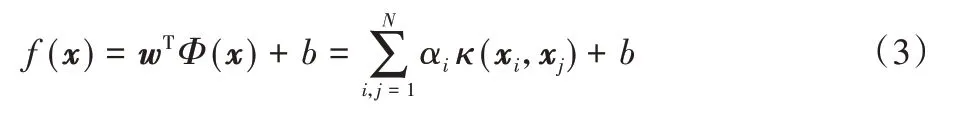
其中：κ(·)被称为核函数，若知道映射函数Φ(x)的具体形式，就可以直接计算出ΦT(xi)Φ(xj)，由此就可以得到具体的核函数κ(·，·)。但在现实应用中通常无法知道Φ(x)的具体形式，但幸运的是，适合的核函数的存在使得在不知道ΦT(xi)和Φ(xj)的具体形式下，也可求得核函数的值。

1.2 多核学习方法

多核学习方法是在训练过程中训练多个基本核函数，然后对这些不同的核函数及其参数进行组合，以获得最优的核组合，结合多种核函数的优点，进行更优的特征映射。

按照合成核构造方法的不同，多核学习方法可以分为以下三种类型［16］。

1）合成核方法。

由于不同核函数具有不同的特性，将多个核函数组合可得到具有不同核函数特性的组合核，称为合成核方法。设有M个基本核函数，可以通过以下几种方法生成合成核矩阵或合成核函数：

①直接求组合核函数：

②加权求组合核函数：

其中μi为核权重系数。

③加权多项式扩展核：

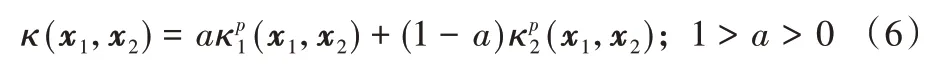
由Mercer 理论可知，通过以上方法生成的组合核函数仍满足Mercer 条件。

2）多尺度核方法。

由于不同尺度的核具有不同的特性，多尺度核方法的思想为将多个不同尺度的核进行融合。经过多年发展，多尺度理论得到了完善，多尺度核方法具有良好的理论基础。多尺度核方法需要找到一组具有多尺度表示能力的核函数，例如高斯核函数就是一种具有代表性的多尺度核函数，设核函数数量为M，其多尺度化形式为：

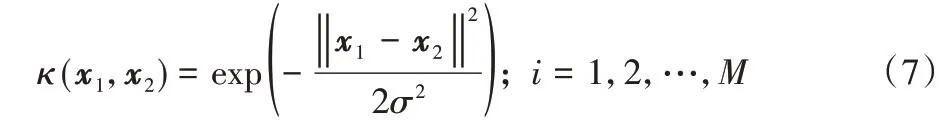
其中：核带宽取不同值，例如σi=2iσ。结合高斯核函数的性质可知：当σi取较小值时，可以更好地处理数据集局部特征；当σi取较大值时，可以得到更好的泛化性能。

通过大尺度核与小尺度核的结合，可以得到更加适合特定数据集的合成核函数，然而此类方法求解过程的时间复杂度较高，且作为SVM 的核函数时，支持向量数量增加较多。

3）无限核方法。

在处理一些大数据集时，使用一定数量的核函数生成合成核的性能并不能完备地表示数据中包含的物理信息，此时将有限个核函数扩展到无限核的方法成为一个重要的研究方向。

无限核方法的构造方法是寻找到多个基本核函数集合中能使凸正则化函数最小化的核，其中基本核集合内可以存在无限个连续参数化的核函数，此类问题在求解时可以使用凸函数差分优化理论或半无限规划来解决。

1.3 基于随机特征映射的四层神经网络

基于随机特征映射的四层神经网络（FRMFNN）模型是如图1 所示的一个四层网络。

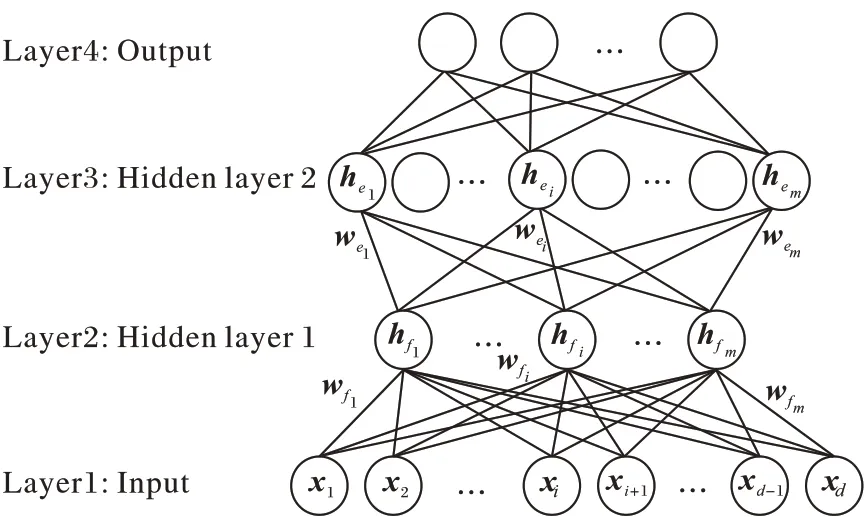
图1 基于随机特征映射的四层神经网络结构Fig.1 Four-layer neural network framework based on randomly feature mapping

设训练样本数为N，特征数为d，类别数为c，则训练集为{(X，T)|X∈RN×d，T∈RN×c}，其中X=[x1，x2，…，xd]为输 入矩阵，T=[t1，t2，…，tc]为对应的输出矩阵。原始输入数据X经过随机映射后组成n组随机特征，这n组随机映射特征组成第一层隐藏层，其中的特征映射函数为ζi(i=1，2，…，n)，记原始输入数据矩阵为X=[x1，x2，…，xd]∈RN×d，于是第一层隐藏层中第i组映射特征为1，2，…，n，其中和是随机生成的权重和偏置矩阵，用于连接输入层到第一层隐藏层中第i组特征节点。

定义

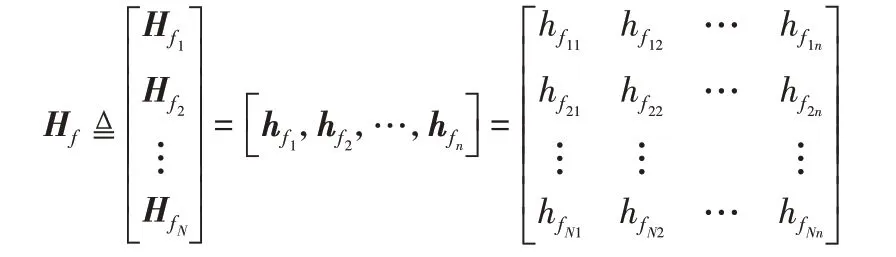
表示第一层隐藏层中N个训练样本的n组映射特征节点集合，然后把Hf传输到第二个隐藏层。

然后，定义第二个隐藏层中第j组隐藏节点的输出为，j=1，2，…，m，其中gj(·)是一个非线性核函数，如sigmoid 等。和是随机生成的连接第一个隐藏层与第二个隐藏层第j组隐藏节点的权重和偏置矩阵。另外，第二个隐藏层的输出定义为：

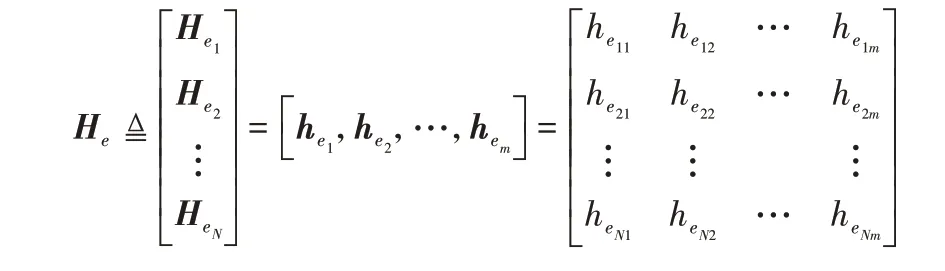
在建立模型时，每一组映射的函数ζi(·)和gj(·)可以选择不同的函数。为了不失一般性，在下文中ζi(·)和gj(·)的下标i和j将被省略。于是，基于随机映射的四层神经网络的数学模型被表示为：

其中：T=[t1，t2，…，tN]T表示训练样本期望的输出矩阵，β是连接第二个隐藏层连接与输出层的权重矩阵。在给出训练样本并且隐藏层神经元参数根据任意连续采样分布概率随机生成之后，隐层输出矩阵Hf和He就是已知的，并且保持不变。则求解式（8）中的β就可以转化为求解线性系统方程He β=T的最小范数最小二乘解，则：

其中He+表示第二个隐藏层输出矩阵He的Moore-Penrose 广义逆。

1.4 特征选择及稀疏化

由于FRMFNN 模型的特征是随机选择的，即通过高斯分布、均匀分布等随机分布函数生成网络的初始权重矩阵wf对数据的原始特征进行随机映射，生成随机映射特征。为了克服这些特征的随机性，并获得输入特征的稀疏化表达，在第一次随机映射时，利用嵌入式特征选择的方式，应用线性逆问题对随机生成的初始权重矩阵wf进行微调，以平方误差作为损失函数，则优化目标为：

当样本特征很多，而样本数相对较少时，式（10）很容易陷入过拟合，为了缓解过拟合问题，在式（10）中引入L1正则化项，则有：

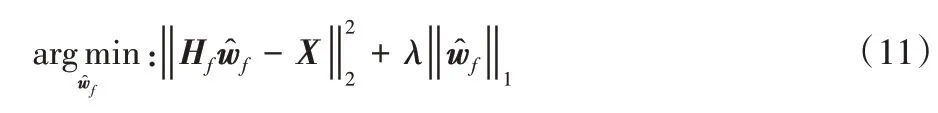
其中：是稀疏自动编码器的解，Hf为初始给定线性方程的期望输出，即Hf=Xwf。L1范数和L2范数正则化都有助于降低过拟合风险，但L1范数比L2范数更易于获得“稀疏”解，即求得的wf会有更少的非零分量，可在降低过拟合风险的同时实现对特征的稀疏编码。

上述问题被定义为lasso［22］，它是一个关于wf的凸函数，此问题可使用交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）［23-24］求解：

首先，式（11）中的问题可以等价为下列一般性问题：

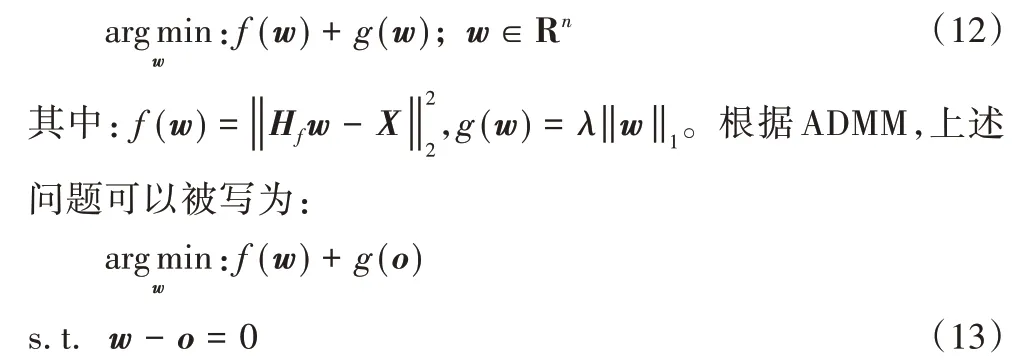
上述优化问题可以通过下列迭代步骤解决：

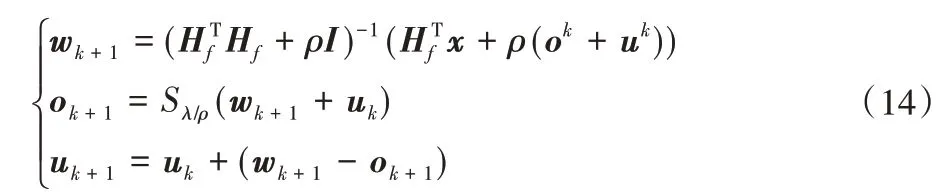
其中ρ＞0，S是软阈值运算符，定义为：

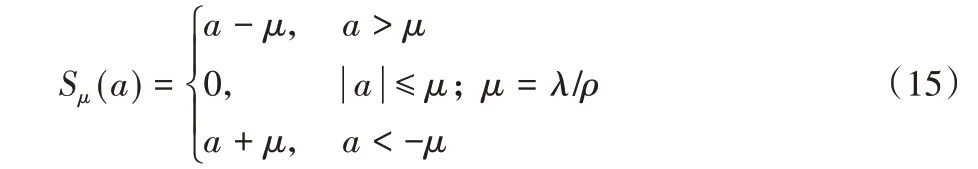
原始特征经过稀疏处理，降低了特征表示的复杂度，减少了系数参数，可以充分挖掘数据中的有用信息，去掉数据信息的冗余部分，达到最大化利用数据的目的，并且提高模型训练速度。

1.5 基于随机特征映射四层的核方法

1.3 节介绍了基于随机特征映射的四层神经网络及其相关算法。该算法对原始特征X=[x1，x2，…，xd]∈RN×d作了两次随机映射，生成两层隐藏层：hf=ζ(Xwf+bf)及he=g(Hfwe+be)，其中ζ为第一层特征映射函数，g（·）为非线性激活函数，最后把映射特征连接到输出层，再计算出输出权重。在计算第一层隐藏层时，通过嵌入式特征选择的方式，对随机特征进行稀疏化处理。受到支持向量机（SVM）的相关核技巧理论的启发，在上述的基于随机特征映射的四层神经网络（FRMFNN）中，可以引入核函数代替特征与权重的内积构建一种基于随机特征映射的核学习方法。

把原始特征x经过映射函数Φ(x)从低维空间转化到高维空间上，理论上计算复杂度会变高很多，但是通过引入核函数可以巧妙地化解这个问题。

例如，将样本点(x1，x2)从二维空间转化到三维空间(z1，z2，z3)，令：

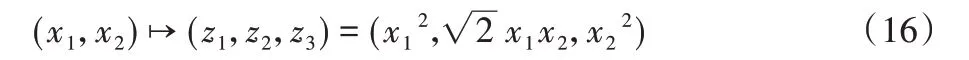
设Φ为映射函数，则：

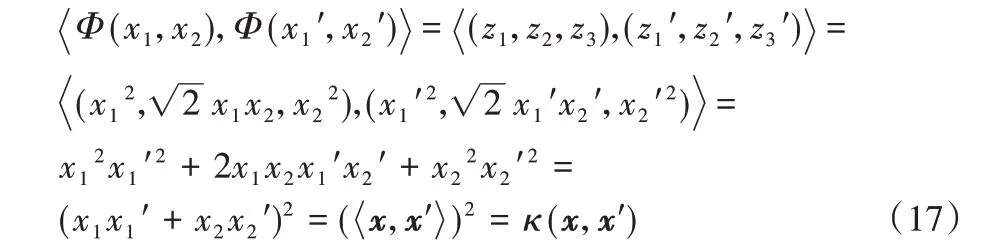
从式（17）可以看出，核函数可以将原始特征空间上的点内积经过某个特定的映射转化为高维空间上的点内积，而不用对高维空间上的点进行具体运算，不仅没有增加计算复杂度，还可以得到特性更好的高维特征。

然而在动物世界中，有一些动物可是天生的长鼻子，与说谎毫无关系。比如，大象拥有世界上最长的鼻子，可以卷起食物，可以吸水洗澡，还可以抵御敌人，用处可大了！那么，除了大象，动物界还有谁也有“长鼻子”呢？

通过在基于随机特征映射的四层神经网络中引入核函数，可以得到原始特征更好的高维投影。设随机特征映射层的输出为H，随机核映射权重矩阵为we，基于随机特征映射的核方法的架构如图2 所示。通过对随机映射特征矩阵H进行随机核映射，生成核映射层，再连接到输出层。

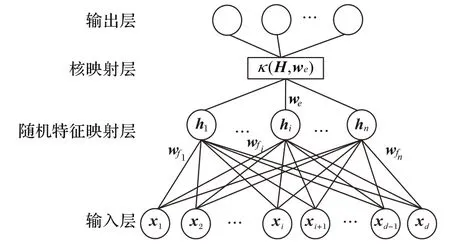
图2 基于随机特征映射四层核方法的架构Fig.2 four-layer kernel method framework based on randomly feature mapping

2 基于随机映射特征的多核组合学习算法

2.1 核函数的选择

设一个训练数据集D有N个样本集合为{{(x1，t1)，(x2，t2)，…，(xN，tN)}∈X×T|X∈RN×d，T∈RN×c}，可以通过一个非线性映射：

把输入数据映射到一个新的特征空间Γ={Φ(x)|x∈X}，其中Γ∈Rd。设κ：XTX→R 是一个连续对称函数，由Mercer 理论［25］可知，κ能作为核函数使用当且仅当这个对称函数所对应的核矩阵K是半正定的。则一定存在一个特征空间Γ和一个映射Φ：X→Γ，使得：

针对不同的应用，可以设计不同的核函数。常用的核函数主要有线性核、多项式核、径向基核、Sigmoid 核等：

1）线性核：

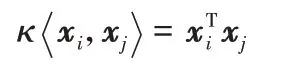
2）多项式核：

κ；m≥1 为多项式的次数

κ；δ＞0是RBF核的带宽

4）拉普拉斯核：

5）Sigmoid核：

κtanh为双曲正切函数，β＞0，θ＜0。

2.2 基本核矩阵的生成

MK-FRMFNN 中的基本核矩阵计算方式与传统的核映射方法有所不同。不再简单地对所输入的样本数据直接进行核映射，而是在映射过程中加入一个随机权重矩阵，将经过一次随机映射并稀疏化之后的特征矩阵与随机权重矩阵做核映射。下面以高斯核函数为例进行具体说明。高斯核函数形式为：

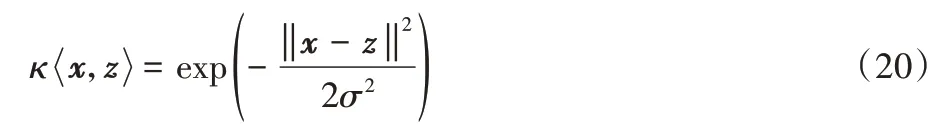
设MK-FRMFNN 中第一层稀疏化的随机映射层的输出为Hf，维度为N×n，连接基本核矩阵的随机权重矩阵为we，维度为l×n，使用高斯核对Hf做随机核映射，则经过核映射生成的核矩阵为：

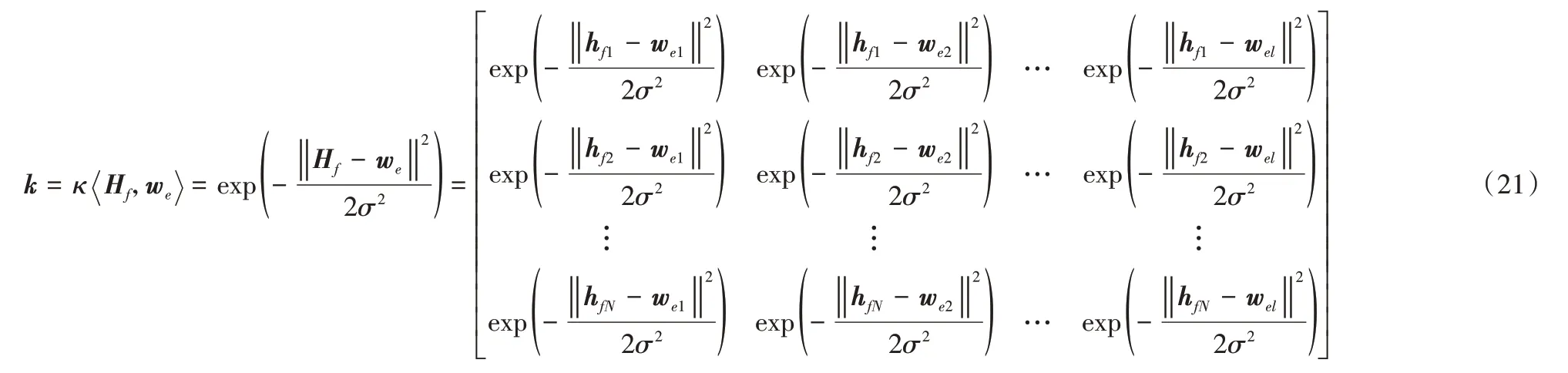
其中：hfi(i=1，2，…，N)为Hf的n维行向量，wej(j=1，2，…，l)为w e的n维行向量，Hf和w e两者通过式（21）所示做随机核映射之后生成的核矩阵k为N×l维实矩阵。核函数选取其他函数时也如上述过程一样求解对应的基本核矩阵。通过控制随机权重矩阵w e的维度l，即可控制基本核矩阵的维度，在进行大规模、大维度样本的学习时，也可以把核空间的维度控制在可控范围。

2.3 基于随机映射特征的核组合学习框架

基于随机映射特征的核组合学习框架如图3 所示。首先使用多个预定义的基本核函数对原始数据的随机映射特征做再次映射生成多个基本核矩阵；然后通过线性组合的方式合成核矩阵，再使用合成核矩阵训练得到分类器或回归函数的最终输出权重β，最后计算得出网络的分类或预测结果。当选择具体的核函数时，若不清楚使用哪个核函数的效果好，则可以先选择高斯核函数进行尝试。

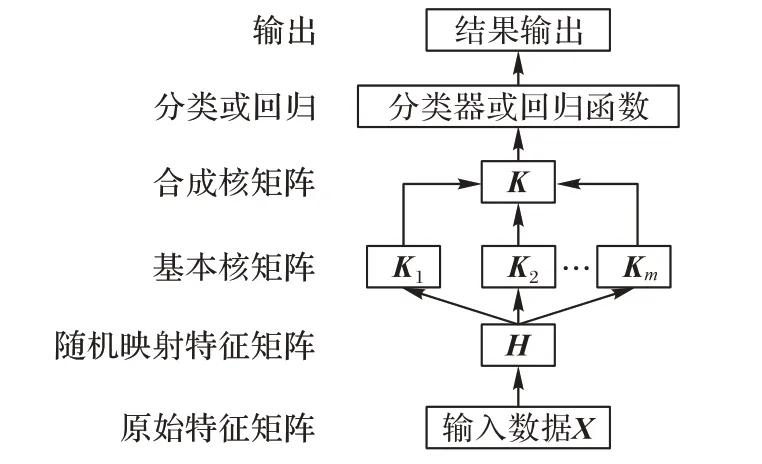
图3 基于随机映射特征的核组合学习框架Fig.3 Multiple kernel learning framework based on randomly feature mapping

多核学习就是将不同特性的核函数进行组合，以期望能获得多类核函数的优点，得到更优的映射性能。组合的方法多种多样，包括线性组合的合成方法、多核扩展的合成方法等。本文主要使用了线性组合的方法中平均求和核的方式，即：

其中：m为基本核矩阵的个数，即K为各个基本核的平均值。与传统的核函数不同，本文所提出的基于随机映射特征的多核学习方法在生成每个基本核矩阵过程中，引入一个随机权重矩阵，把对随机映射特征的核映射过程转化为随机特征核映射，也就是把随机映射特征经过再次的随机核映射投影到核空间，即使核矩阵中的z取值为随机生成的权重矩阵we，使得随机映射特征H经过we的再次随机核映射生成基本核矩阵，即，这样可以通过控制生成的随机权重矩阵的维数来控制核矩阵的维度，并且通过结合不同的随机权重，可以集合多类随机分布函数的特性，从而取得更好的映射特征。

2.4 两种多核组合方式及其算法流程

本文中提供两种不同的核映射方式进行多核学习：1）每个基本核选取随机映射特征中的部分特征进行核映射，再进行核组合；2）每个基本核取数据的全部随机映射特征进行核映射，然后进行核组合。两种基于随机映射特征的多核组合学习算法步骤如下：

算法1 MK-FRMFNN 基本算法。

输入：训练数据集D，基本核矩阵的参数，正则化参数λ；

输出：最终连接权重β。

步骤1 计算第一层隐层输出H

步骤1.1 随机生成特征映射权重wf和偏置bf

步骤1.2 通过式（14）利用稀疏编码器求出wf的稀疏解，并得到稀疏的映射特征H=ζ(Xwf+bf)

步骤2 生成基本核矩阵：

每个核矩阵取全部随机映射特征H做核映射，即Ki=

或把H随机分成m份，每个核矩阵取部分特征做核映射，即Ki=

步骤3 合成核矩阵K=

步骤4 计算输出层连接权重β=K+T

MK-FRMFNN 算法的时间复杂度主要包括四个部分，分别对应上述算法过程中的四个步骤。步骤1 中计算随机映射特征节点集合的时间复杂度为O(iter·Ndn)，其中iter为稀疏自动编码器的迭代次数，N为输入训练样本数，d为输入样本的特征维数，n为随机映射特征的特征维数。步骤2 中生成每个基本核矩阵的过程主要是N×n和li×n的两个矩阵按照式（21）的方式做核映射，计算的时间复杂度为O(Nnli)，则生成m个基本核矩阵的时间复杂度为，其中li，i=1，2，…，m为每个基本核矩阵的维数。在步骤3 中，生成合成核矩阵采用矩阵求和再求平均的方式，每个基本核矩阵的大小为N×li，在算法中设li大小相同，记为l，则有m个N×l维基本核矩阵相加，因此生成合成核矩阵的时间复杂度为O(mNl)。在步骤4 中，计算伪逆时，当L≤N，即合成核矩阵维数小于训练样本个数，此时时间复杂度为O(L2N)；而当训练样本数小于隐层节点个数，即L＞N时，伪逆计算的时间复杂度为O(N2L)；计算输出权重的时间复杂度为O(LNc)，其中，L为合成核矩阵的维数，L=，c为目标类别数。

综上所述，FRMFNN 基本算法的时间复杂度为：

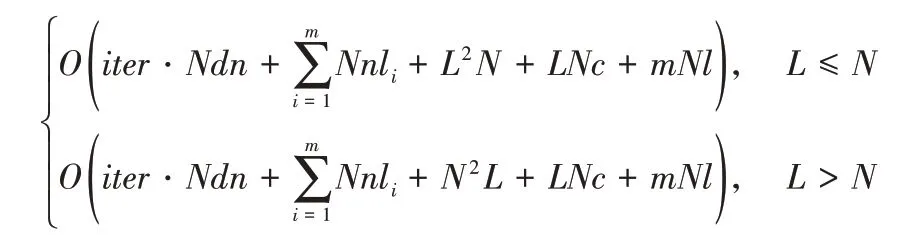
步骤2 中两种核映射方式在时间复杂度上没有区别，在映射方式上也相同，只在特征空间的选择上存在差异。前者随机性较大于后者，但是特征规模上小于后者；后者在每个核映射中包含的特征信息比较完整，但可能造成过多的数据冗余。两种映射方式在进行核组合之后的核矩阵所包含的特征信息都是完整的，所以在最后的输出结果上没有太大差异，在数据特征规模较小时可以选取第二种方式，在数据特征规模较大时，第一种方式较为适用。

2.5 网络权重的正则化训练

给定N个训练样本{X，T}，特征域X∈RN×d，目标域T∈RN×c，设MK-FRMFNN 网络第一层隐藏层具有n个隐藏层神经元，其特征映射函数为ζ(·)，则经过第一次随机映射及稀疏化之后的特征矩阵为H=ζ(Xwi+bi)，i=1，2，…，n，其中wi和bi是随机权重和偏置，根据任意连续采样分布概率随机生成。对随机映射特征H进行不同的核映射生成多个基本核矩阵Ki，i=1，2，…，m，然后将这些基本核矩阵组合成核矩阵K，则网络的数学模型可表示为：

其中β是连接合成核矩阵与输出层的权重矩阵，可通过K的伪逆的岭回归近似算法计算得出，即：

其中K+表示合成核矩阵K的Moore-Penrose 广义逆。

上述伪逆快速学习算法是对线性方程组的最小二乘估计，是一个基于经验风险最小化原理的学习过程，其优化目标是在训练误差最小的情况下获得输出权值，即

式（25）训练出的模型容易产生过拟合现象，为了缓解过拟合问题，可对式（25）引入正则化项。在正则化方法中，将一项L2惩罚项加入到损失函数中，这成为了L2正则化，它也被称为岭回归（Ridge regression），由此下列优化问题成为求解伪逆的另一种方法：

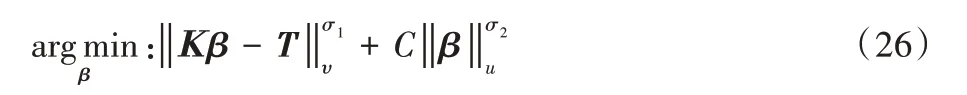
其中：σ1＞0，σ2＞0，υ，u是典型的规范正则化为正则化项。通过取σ1=σ2=u=υ=2，将上述优化问题转化为L2范数规范正则化，C是对β的加权平方和的进一步约束，该解决方案与岭回归理论等价——通过在KTK或KKT的对角线上加上一个整数来近似Moore-Penrose 广义逆。

设需要被最小化的目标函数如下：

对β进行微分可以得到：

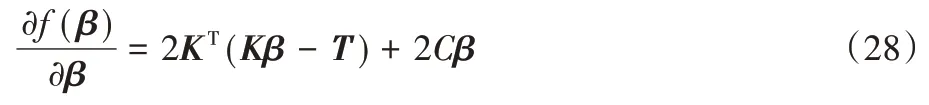
让梯度为0，可以得到：

易得：

因为C＞0，矩阵CI是正定的，又因为矩阵KTK是半正定的，因此矩阵CI+KTK是正定的。由于CI的出现，使得CI+KTK是非奇异矩阵，所以CI+KTK可逆。又β=K+T，因此，有

于是可得

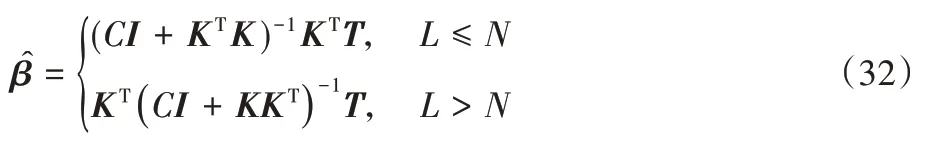
其中：当L≤N时，即合成核矩阵特征维数L小于训练样本个数，此时I为L×L维单位矩阵；而当训练样本数小于合成核矩阵特征维数，即L＞N时，利用Woodbury 公式可以等价地求出β^，此时I为N×N维单位矩阵，显然这种情况下计算N×N维逆矩阵要比计算L×L维逆矩阵高效得多。这样，就可以快速地求出网络的输出权重。

3 实验及结果分析

3.1 实验环境及实验数据

为了检验基于随机映射特征的多核组合模型的分类性能，本节在多个UCI 分类数据集［26］上进行了实验，分别为：Letter、Robot（Robot Navigation）、Ecoli、ACT（ACTivity recognition）、Adult、Australian、Eye state、Magic、Car，包含了大样本数据集和小样本数据集、多分类和二分类数据集、低维数据集和高维数据集。对于每个数据集，随机选取70%作为训练样本，剩余的30%作为测试样本，并且对类别数作onehot 编码。所有实验进行之前对原始数据进行线性归一化处理，即：

数据集的信息在表1 中列出。

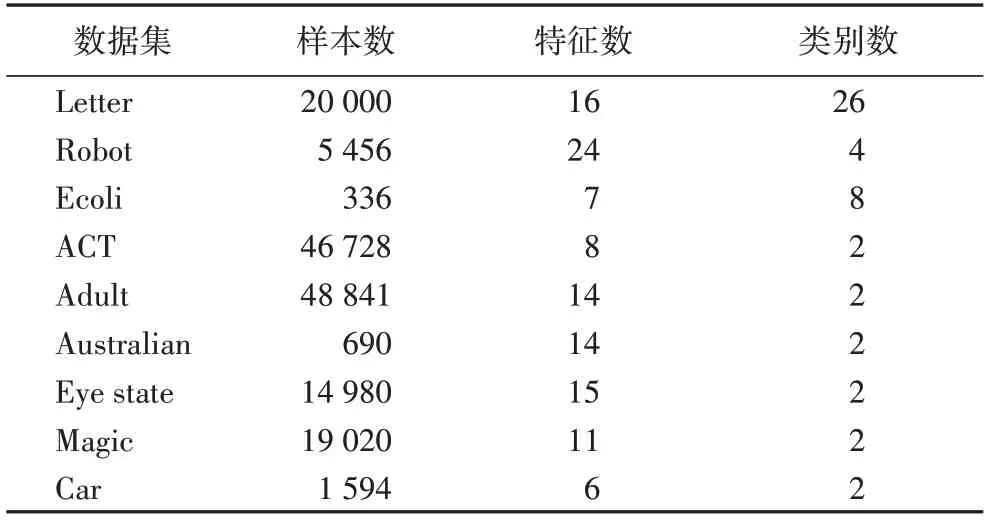
表1 数据集的详细信息Tab.1 Details of datasets

为了检测MK-FRMFNN 多核学习算法的效果，对于所有数据集，选取FRMFNN、BLS 模型算法进行比较。为保证实验结果的真实准确，每个数据集对应的分类实验都进行了10 次实验，然后计算其平均值和标准差作为最终结果。对于分类问题，本文采用常用的准确率（accuracy）作为衡量指标。本文所有实验均在同一环境下完成，采用在Windows 10 环境下搭建系统，计算机处理器配置为Intel CoreTM i5-10210U CPU 1.60 GHz，内存16 GB，主算法在Python 3.7 中完成。

3.2 实验参数设置

在实验中，BLS 模型和FRMFNN 单核模型的岭回归的正则化参数C根据先验经验通过网格搜索从{2-24，2-23，…，23}中确定。为了提高效率，采用分组映射的方式对原始特征进行随机映射，所以实验过程中存在三个参数：第一层隐藏层的随机映射特征个数Nf和映射组个数Nm，第二层隐藏层节点维数Ne。通过网格搜索分别从［1，20］，［1，20］，［1，13 000］范围内搜索，第一次随机特征映射时所进行的稀疏化处理过程中的参数λ为0.01，迭代次数设置为50。MKFRMFNN 模型的参数参考其单核模型对应的同一数据集参数，随机映射特征个数Nf和映射组个数Nm在单核FRMFNN对应参数附近±2 范围内搜索，基本核矩阵维数在对应的单核FRMFNN 模型的[ 0.8×Ne/m，1.2×Ne/m]范围内进行网格搜索，m为基本核矩阵个数。

由于MK-FRMFNN 的参数比较多，加上正则化参数的寻优范围较大，为了让网格寻优减少参数范围，本文先对正则化参数C做一系列实验，确定正则化参数的范围。首先选择Ecoli、Australian、Car 三个数据集设置正则化参数为{2-24，2-23，…，2-10}分别进行实验，Ecoli 数据集的其他参数［Nf×Nm，Ne，σ1，σ2］设置为［2×2，41，10-2，10-1］，Australian 数据集的参数为［6×3，28，10，102］，Car 数据集的参数为［5×2，390，1，102］。实验结果在表2 中显示。

由表2 可以看出，当正则化参数C接近于0 时，正则化参数的变化对实验结果的影响不大，且网络性能较好；当正则化参数不断增大时，预测精度呈现下降的趋势，所以后续实验中的正则化参数皆设置为2-24，不再参与网格寻优。

表2 在不同正则化参数下的实验结果 单位：%Table 2 Experimental results with different regularization parameters unit：%

在MK-FRMFNN 实验中设置两种基本核函数，分别是一个Sigmoid 核函数=tanh(xTz+b)，其中b=-0.1；两个高斯核函数，带 宽σ从{10-2，10-1，…，102}中通过网格寻优选取。在生成初始权重时可以选择任意的随机分布，如高斯分布、均匀分布等。在实验中，由于对初始特征毫无了解，而对于初始特征的随机选择应该是不具有偏向性的，所以实验中初始随机权重wf、偏置bf抽取自［-1，1］的标准均匀分布。在核映射的过程中，对于每一个基本核本文都选择不同的随机分布函数来生成基本核矩阵，这样可以集合多类随机映射函数的优点，获得更优的映射特征组合。Sigmoid 核和第一个高斯核的随机权重矩阵抽取自服从N（0，1）的标准正态分布，第二个高斯核函数的随机权重矩阵抽取自服从［-1，1］的标准均匀分布。各个模型的参数设置详见表3。

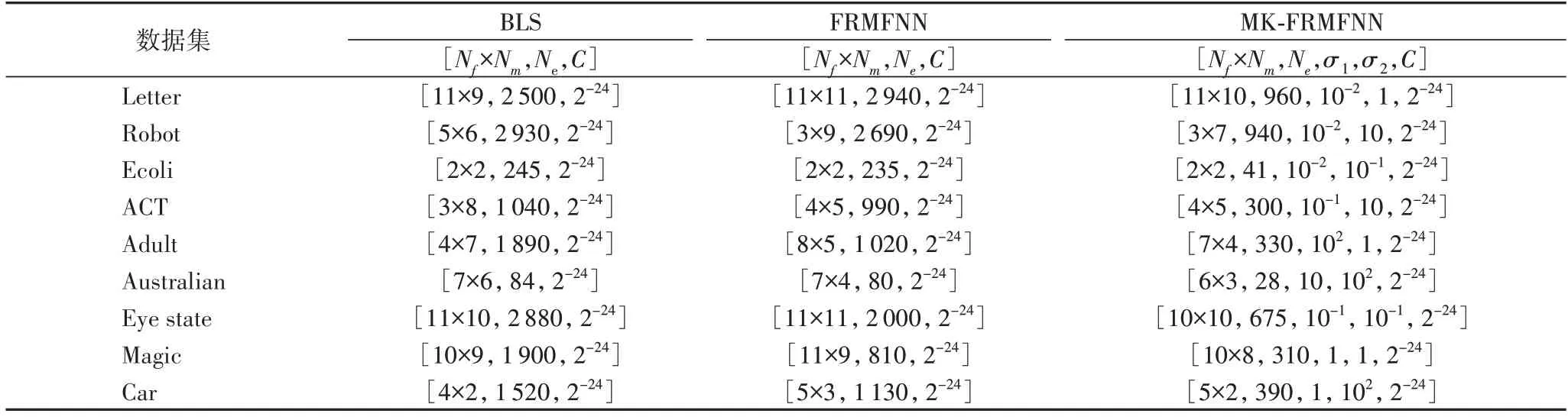
表3 BLS、FRMFNN和MK-FRMFNN模型的参数设置Tab.3 Parameter settings of BLS，FRMFNN and MK-FRMFNN models

在实验过程中，尝试与现有较为先进的其他多核模型作对比，而由于数据集样本规模较大，在现有多核算法模型中进行核化处理后，所生成的核矩阵维数过大会造成严重的“维数灾难”。这种由于样本规模大而造成的高维空间维数灾难问题，通过特征降维也无法得到很好的解决。对于大样本数据集，GLMKL、NLMKL、simpleMKL 以及新近的easyMKL等多核算法在普通计算机上运算非常耗时，需要很多天来完成一次运算，且常面临着计算机内存不足的风险，是非常不现实的。故本文在实验中舍弃了在大样本数据集上与此类算法的对比，选取了Ecoli、Australian、Car 三个小样本数据集与simpleMKL、easyMKL、GLMKL 及NLMKL 四种多核算法进行对比实验，对比算法的实验中设置两种基本核函数，分别是：一个多项式核函数=(xTz+b)2，其中b=1，5 个核带宽分别为σ={10-2，10-1，…，102}的高斯核函数=。其中的参数选用对应参考文献中推荐的参数，采用网格寻优法在推荐值附近进行寻优，正则化参数C的寻优范围为{2-5，2-4，…，25}，另外easyMKL 的参数λ的寻优范围为{0.1，0.2，…，1}，GMKL 和NLMKL 均取默认的L1 范数。所有多核学习对比算法的收敛阈值都设为0.01，最大迭代次数设置为50。Australian 和Car 数据集都是二分类问题，直接进行分类不用做特殊处理，而对于Ecoli 数据集的多分类问题，采用广泛使用的“一对一”（One vs One，OvO）策略将多分类任务分解为多个二分类任务进行实验。

3.3 实验结果及分析

在本节中，对比了BLS 模型、FRMFNN 模型和MKFRMFNN 模型在多个UCI 数据集上的分类精度，实验结果在表4 中显示。

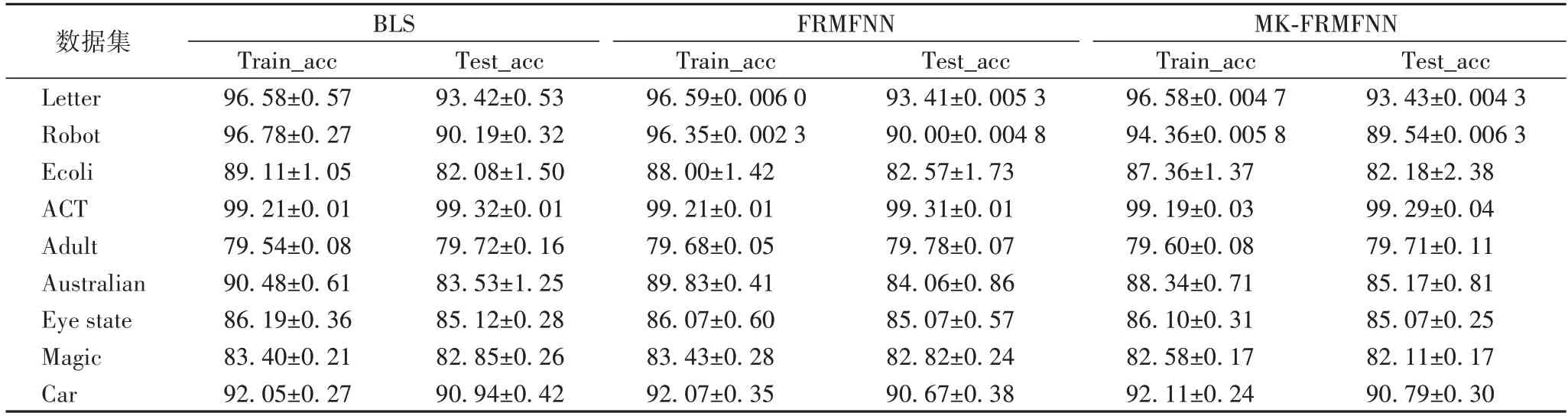
表4 BLS，FRMFNN和MK-FRMFNN模型在用于分类的数据集上的准确率比较 单位：%Table 4 Accuracy comparison of BLS，FRMFNN and MK-FRMFNN models on datasets for classification unit：%

然后选取了Ecoli、Australian、Car 三个数据集与上文中所述的多个主流多核算法进行了精度和时间上的对比，实验结果及参数设置在表5 中列出。

表5 三个数据集上的实验参数及结果Tab.5 Experimental parameters and results on three datasets

结合表3、4 的实验数据可以看出，对于各个数据集，MK-FRMFNN 算法隐藏层节点规模皆远远小于BLS 和FRMFNN 单核模型的隐藏层节点规模，但是都能达到与单核模型相当的分类性能，在Australian、Car 等数据集上达到更高的性能。可以看出，当MK-FRMFNN 模型的核矩阵维数Ne与单核FRMFNN 模型的分类性能达到一致时，多模型隐藏层节点数规模只需要单核模型的1/3 左右，有效说明了通过多核学习的方式可以有效降低FRFMNN 模型的隐藏节点规模，并且能够保持良好的分类性能，体现了MK-FRMFNN 模型的有效性。

由表5 中的实验数据可以看出，对于三个数据集，MK-FRMFNN 算法相比其他多核算法都有较为优异的性能，可见所提算法能够利用多种不同的随机分布函数有效对数据集中的信息进行挖掘，再结合多种核函数对特征进行高维映射，能够有效利用各种核函数的优势，获得良好的分类性能，体现了MK-FRMFNN 算法的优势。

4 结语

针对单特征空间的单核模型存在的核函数选择在很多场景下无法满足应用需求的问题，本文提出了一种基于随机映射特征的多核组合学习方法。该方法通过原始输入特征进行随机映射生成随机映射特征，再通过多个基本核映射投影到核空间，利用在核映射过程中引入随机权重的方式，对随机映射特征做随机核映射，这样在集合多类分布函数特征的同时，可以控制核空间的大小，得到更满足需求的映射特征。最后，把各个基本核矩阵组成合成核矩阵，再通过输出权重连接到输出层。将所提方法应用于常见的分类数据集中做了大量实验，与BLS 算法、FRMFNN 单核模型算法进行比较，并与多个主流多核算法进行了对比实验，在训练精度上体现出了MK-FRMFNN 的有效性。由于算法中参数过多，选取最优的核组合系数存在一定难度，下一步我们将对随机映射神经网络多核模型的核组合方式进行更加深入的研究，对其核组合方式提出更优的解决方案。