社交网络中基于K核分解的意见领袖识别算法

李美子，米一菲，张 倩，张 波，2，3*

（1.上海师范大学信息与机电工程学院，上海 201418；2.上海师范大学人工智能教育研究院，上海 201418；3.上海智能教育大数据工程技术研究中心（上海师范大学），上海 200234）

0 引言

社交网络中意见领袖可以在信息传播过程产生巨大的作用，其发表的言论、持有的态度等一系列行为和后续影响力可以通过用户之间的链接关系产生逐层裂变式扩散［1］。这种扩散效果促使意见领袖对于预测信息传播状态、监督和引导舆论，以及影响网络信息扩散趋势有着极其关键的作用［2-4］。因此，如何发现并识别社交网络中的意见领袖群体是当前社交网络研究的热点问题。

目前，对于意见领袖识别算法的研究主要分为三个方面：一是基于对网络拓扑的分析来检测意见领袖，使用网络拓扑分析社交网络图模型的相关特性，例如，在意见领袖挖掘中，度中心性、中介性中心性、接近中心性和K 核等都是非常有效并且常用的方法［5-7］。二是基于社交网络中用户的历史行为数据挖掘意见领袖。朋友的数量、发布信息的总数、转发或评论信息的总数，以及信息所表达的情感都可以用来识别意见领袖［8-9］。三是综合考虑社交网络的网络拓扑和用户的历史行为数据来挖掘意见领袖。然而，这三种方法都存在以下问题：在大型社交网络中识别意见领袖时通常需要很大的计算量。尽管在社交网络中并不是每一个用户都有足够的条件成为意见领袖，但当前的意见领袖识别算法大多以相同的方式来评估每个用户的重要性。

考虑到上述问题，本文提出基于K 核分解的CR（CandidateRank）算法来识别意见领袖。该算法依据K 核分解的基本原理，结合所设置的分解规则，判定用户是否为意见领袖的概率，将具有较大K 核值的用户加入到建立的意见领袖候选集中，加入意见领袖候选集的用户数由用户的需求决定；然后提出用户相似性的概念，其包括位置相似性和邻居相似性，依据K 核值、入度数、平均K 核变化率和用户追随者个数等来计算用户相似性，最终根据用户相似性对候选集中的用户计算全局影响力，以获得所需的意见领袖。在实验部分使用两种评价指标在三个大小不同的数据集上对该算法选出的意见领袖集进行评估，并通过与其他三种识别意见领袖的算法对比来验证本文算法的可行性。

对于大规模网络，特别是用户关系比较集中的一些网络，其中大部分用户都属于“边缘用户”，他们几乎没有成为意见领袖的潜质，但是根据一些意见领袖识别算法依然要对他们进行计算，极大延长了整体的计算时间，而本文提出的CandidateRank 算法通过建立意见领袖候选集解决了这个问题；另外本文提出的用户相似度的计算通过拓扑结构建立用户位置向量也是比较轻量级的计算。

本文的主要工作有：

1）基于K 核分解区分社交网络中的潜在意见领袖与普通用户。在潜在意见领袖（意见领袖候选集）中识别意见领袖，能够避免重复计算“边缘用户”的重要度，从而降低计算的复杂度。

2）提出平均K 核变化率的概念和计算方法，将它作为判断位置相似性的指标之一；提出用户相似性包括位置相似性和邻居相似性的概念和计算方法，以及一种有效的全局影响力的计算方法。

3）对社交网络图模型进行K 核分解后，具有较大K 核值的用户有较大的可能性是意见领袖，因此可以将具有最大K核值的用户加入到意见领袖候选集中。

1 相关工作

研究表明，K 核分解可以识别社交网络中最具影响力的节点［10］。根据用户的K 核值，可以粗粒度地区分社交网络中的潜在意见领袖与普通用户。CandidateRank 算法的主要工作是基于K 核分解获得潜在的意见领袖加入到意见领袖候选集中，然后依据平均K 核变化率、用户相似性等指标对候选集中的用户进行全局影响力计算，以获得所需的意见领袖。

近年来，识别意见领袖的模型根据是否基于K 核分解可以分为两类：和K 核分解相关的算法、和K 核分解无关的算法。与K 核分解无关的算法比较灵活，Li 等［11］提出了一种基于连续时间马尔可夫链的动态信息传播模型来寻找有影响力的节点组。Aghdam 等［12］提出根据用户之间的信任关系计算用户的总信任值以评估出意见领袖。Xia 等［13］通过评估用户在Twitter 中的行为来计算用户影响力。Zhou 等［14］提出了一种扩展的独立级联模型——EIC（Extended Independent Cascade model）和一种影响力最大化算法GAUP（Greedy Algorithm based on User Preference），结合用户对信息的偏好，找到对于特定信息主题，能够得到最大影响力的种子节点集。陈志雄等［15］提出了基于回帖者的情感倾向挖掘意见领袖。

与K 核分解相关的算法多集中于基于K 核值影响力算法改进，区分具有相同K 核值的节点的影响力，使得意见领袖的识别更加有效或准确。例如，Wei 等［16］综合考虑边两端节点的度，构造加权网络，提出加权K 核分解方法。Yang等［17］定义局部K 核值总和（Local K-Shell Sum，LKSS），计算给定节点相邻2 跳邻居的K 核值之和，再通过计算与给定节点直接相连的节点的LKSS 总和（Extended LKSS，ELKSS）来对节点进行排名。Zeng 等［18］同时考虑节点的K 核值和分解过程中被移除节点的K 核值，提出一种混合度分解（Mixed Degree Decomposition，MDD）算法。Bae 等［19］根据邻居节点的K 核值来估计节点在网络中的影响力，提出扩展近邻核（Extended Neighborhood Coreness，Cnc+）。Liu 等［20］认为网络中某个节点到网络最内核的距离能够决定该节点的传播影响力，这里网络中的最内核是指通过K-Shell 分解后，网络中具有最大K 核值的节点（或节点集）；在此基础上，提出了一种改进的中心性度量方法θ。Hou 等［21］结合度中心性、介数中心性和K-Shell 分解定义了一种all-around nodes。Tong等［22］提出结合K-Shell 分解与接近中心性对网络中节点的传播影响力进行排序，其主要思想是：如果某个节点有较大的传播影响力，那么该节点除了拥有较大的K 核值以外，还应该与网络中其他节点之间的平均最短距离较短。和K 核分解相关的算法主要针对无法对比具有相同K 核值的节点之间的重要度的问题进行改进，往往都是在K 核分解的基础上计算社交网络中所有节点的影响力。

2 算法和相关定义

2.1 算法结构

如图1，对全体用户进行K 核分解找出意见领袖候选集L，对L中的候选者进行平均K 核变化率和用户相似性计算，最终得到全局影响力。

图1 CandidateRank算法结构Fig.1 CandidateRank algorithm structure

2.2 算法步骤

用于检测意见领袖的CandidateRank 算法步骤主要分为三个：

步骤1 用K 核分解获取社交网络中每个用户的K 核值，并选择K 核值最大的用户加入到意见领袖候集中。

步骤2 通过多次使用K 核分解，分别计算删除意见领袖候选集中的用户后所造成的平均K 核变化率，用于步骤3中评估位置相似性。对于意见领袖候选集中的每个用户，找到该用户的追随者集合，以及追随者的追随者集合，用于步骤3 计算意见候选集中的用户和其追随者的邻居相似性。

步骤3 评估意见领袖候选集中每个用户和其追随者的位置相似性和邻居相似性，计算用户全局影响力以识别意见领袖。

2.3 相关指标

接近中心性（Closeness Centrality）［23］：是节点到网络中所有其他节点最短路径之和的倒数，表示节点在网络中与其他节点的距离，接近中心性越大，则用户与其他用户的距离越近。

中介中心性（Betweenness Centrality）［24］：是穿过节点的最短路径占网络中最短路径的比例。

特征向量中心性（Eigenvector Centrality）［25］：基于邻居节点的重要度评估节点重要性。

Katz 中心性（Katz Centrality）［25］：在特征向量中心性的基础上，给和节点直接连接的邻居以及间接连接的邻居分配不同的影响力权值。

肯德尔相关性系数（Kendall’tau）：是一种秩相关系数，计算式如下：

其中：nc与nd分别代表两个列表中的相容元素对与不相容元素对的数量。n是列表长度即列表中元素数，两个列表的长度相同。

2.4 算法相关定义

一些社交平台中用户与用户之间会通过一些方式产生公开交互，如微博、Facebook、豆瓣等，用户与用户之间的行为可以构成社交网络，本文将这样由用户和用户间交互关系构成的社交网络转化为一个有向图G=(V，M)，其中V={u1，u2，…，uN}是社交网络中的节点（用户）集合，N是节点（用户）总数，E={e1，e2，…，eM}是边的集合，边表示用户之间的互动关系，如评论、点赞、转发等行为在用户间建立起有向关系（即有向边），M是社交网络中边的总数。

定义 1K核值。在图G中，若存在子图Gk={(Vk，Ek)，Vk⊆V，Ek⊆E}，对每个节点v∈Vk，v的度（出度及入度）大于或等于k，则图的子图Gk是图的K 核。K 核值是经过K 核分解分配给图中每个节点的重要度分值，并且当v∈V，v∉Vk时，v的K 核值等于k。

定义2全局影响力。在社交网络中，用户的影响力通过追随者向外扩散。用户的追随者越多，其在社交网络中影响力的扩散范围越大，即全局影响力越大。本文用户全局影响力用inf(u) 来表示，其大小计算考虑多种影响因素（第3章详细阐述）。

定义3追随者。在社交网络图中，若存在u，v∈V，ek∈E同时ek={u，v}，则用户u是用户v的追随者。

定义4意见领袖。在社交网络中，用户的影响扩散范围越大，可理解为用户的全局影响力越大，影响力最大的用户即为意见领袖，意见领袖在大众传播过程中起到引领作用。

定义5意见领袖候选集（潜在意见领袖）。在计算用户重要度之前，选择最有可能成为意见领袖的用户加入到意见领袖候选集L中，V、O、L之间的关系为O⊆L⊆V。

定义6意见领袖集。意见领袖集O是节点集合V的子集，由集合V中的s个节点组成，并且满足条件min{inf(v)}＞max{inf(u)}，v∈O，u∈V，u∉O，s是由实际需求决定的。普通用户是除O以外的其他用户，用C表示，且C=V-O。

本文中有4 种用户角色：追随者、普通用户、意见领袖候选者和意见领袖，它们的关系可以用图2 表示。

图2 用户角色关系Fig.2 User role relationship

3 基于K核分解的CandidateRank算法

在社交网络中，并不是所有的用户都有可能是意见领袖，例如新加入社交网络并没有得到其他人关注的用户，或者在数据收集时被遗漏了大部分追随者的用户，这些用户在所分析的社交网络中成为意见领袖的可能性均较小。在识别意见领袖的过程中，没有必要对这些用户的重要度进行评估；并且，在社交网络中，大部分用户是普通用户，只有少数用户是意见领袖。因此，在评估用户重要度之前，可以通过选择意见领袖候选集来过滤掉大部分的普通用户。相对于所有用户，在具有较少用户的意见领袖候选集中确定意见领袖，既可以提高意见领袖识别的效率，又可以增强算法对于大规模社交网络的适用性。

通过K 核分解得到的最具影响力的节点是一个集合，集合中节点的具体重要度并不明确。通过K 核分解，选择K 核值最大的用户加入意见领袖候选集，一方面避免了无法选择区分普通用户和潜在意见领袖的标准的问题，另一方面当具有最大K 核值的用户总数不足时，可以选择具有次大K 核值（即排名第二大的K 核值）的用户补充到意见领袖候选集中。

3.1 K核分解

K 核分解迭代地删除社交网络图中度小于k的节点及其连边，得到子图：k-核，k-核中每个节点的度值均等于或大于k。当图中的某个节点存在于图的k-核中，而不存在图的k+1-核中时，该节点的K 核值等于k。K 核分解确定了社交网络中每个节点的K 核值，其具体步骤如下：假设社交网络中每个节点的度均大于或等于1，整个社交网络图是G的1-核G1；然后，迭代地删除G1中度小于2 的节点及其相关的边，得到的子图G2是图的2-核，被删除的节点存在于图的1-核中，而不存在于图的2-核中，所以被删除节点的K 核值等于1。接下来，迭代地删除G2中度小于3 的节点及其相关的边，得到的子图G3是图的3-核，被删除的节点存在于图的2-核中，而不存在于图的3-核中，所以被删除节点的K 核值为2。以此类推，直到得到社交网络中所有节点的K 核值。

选择具有最大K 核值的用户作为意见领袖候选集L。当具有最大K 核值的用户总数少于所需意见领袖总数时，将具有次大K 核值的用户加入到意见领袖候选集L中。K 核分解得到的用户是在图中受到最多用户关注或者和最多用户有联系的，因为他们成为意见领袖的概率非常大。

3.2 平均K核变化率

在意见领袖候选集中，具有相同K 核值的用户，其用户重要度也不尽相同。在复杂网络的节点重要度研究中，删除法通过对比删除节点前和删除节点后网络的连通性变化情况对节点重要度进行排序。在本文中，意见领袖候选集中的用户本身具有最大的K 核值，是社交网络中较重要的用户。因此，考虑通过对比删除某个用户前后其他用户K 核值的变化情况，计算出平均K 核变化率，来说明该用户对网络中其他用户的平均影响力。平均K 核变化率的计算式如下：

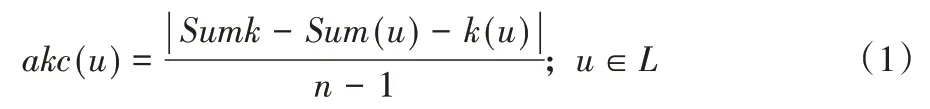
其中：Sumk是社交网络G中所有用户的K 核值总和，k(u)是社交网络G中用户u的K 核值，Sum(u)是社交网络G去掉用户u及其连边后其他用户的K 核值总和，n是社交网络中的用户总数，L代表意见领袖候选集。以图1（a）为例，对于用户2，首先用户总数n=19，再计算图中网络每一个用户的K核值，由图中节点的颜色可明显看出该图中的最大K 核值为4，而Sumk=36；同样，由图明显得到k(2)=3。图1（b）描述的是去掉用户2 及其连边之后的过程，可看到此时其他用户的K 核值总和Sum(2)=30。综上计算出akc(2)=0.167。

3.3 用户相似性

在社交网络中，用户通过与其他用户交互，扩散自己的影响力，提高自己的重要度。平均K 核变化率能够反映用户在整个社交网络中对其他用户的平均影响力，但在评估用户交互过程中扩散影响力的能力时需要考虑相似性因素。用户与其追随者的相似性对追随者对该用户的影响力扩散情况造成影响。在本文中，将相似性分为位置相似性和邻居相似性。

位置相似性 位置相似性评估用户在社交网络拓扑位置上的相似性，通常情况下，常用度中心性、中介中心性、紧密中心性、特征向量中心性等中心性指标来说明用户在社交网络拓扑上的位置，但中介中心性、紧密中心性和特征向量中心性的计算均涉及全网用户，计算复杂度较高。同时，在有向图中，入度数比出度数更能体现用户的中心性，本文选择入度数和K 核变化率表征用户在社交网络中的拓扑位置。此外，由于在选择意见领袖候选集时，可能会加入具有次大K 核值的用户，候选集中用户的K 核值并不完全相同。因此从K 核值、入度数、K 核变化率三个方面考虑用户的位置相似性，构建位置特征向量：

则用户u和用户v的位置相似性p_s(u，s)计算式为：

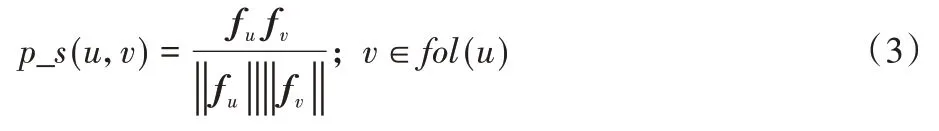
其中：fol(u)是用户u的追随者集合，也就是在社交网络中关注用户u的用户集合；fu是用户u的位置特征向量，fv是用户v的位置特征向量。如图1（c），用户2 的位置特征向量为f2=(3，4，0.167)，其追随者1的位置特征向量为f1=(4，1，0.056)，因此p_s(2，1)=0.55。

邻居相似性 邻居相似性用来评估两个用户的追随者之间的相似性。假设v是u的追随者，且v一定能接收到u的信息。在极端情况下，当u和v的追随者之间没有相同用户时，u的信息能够通过v被网络中的更多人接收；而当v的追随者都是u的追随者时，u的信息无法通过v进行传播。因此邻居相似性与用户的信息扩散能力呈反比，这里计算用户u和用户v的邻居相似性为n_s(u，v)：

以图1 为例，用户2 有四位追随者，用户1 有一位追随者，其中用户4 是他们的共有追随者，于是n_s(2，1)=0.25。

3.4 用户全局影响力

在社交网络中，用户的影响力通过追随者向外扩散。用户的追随者越多，其在社交网络中影响力的扩散范围越大，即重要度越大。但不同追随者对用户影响力的扩散意愿并不相同，追随者的扩散意愿越大，用户的影响扩散范围越大，可理解为用户的全局影响力越大，影响力最大的用户即为意见领袖。

本文使用用户间的位置相似度评估不同追随者对用户影响力的扩散意愿，提出用户全局影响力的计算式如下：

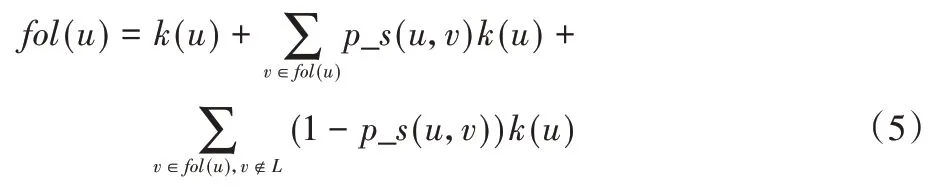
当用户及其追随者都是意见领袖候选者时，追随者与用户的位置越相似，则追随者转发用户信息的可能性越大；当用户追随者不是意见领袖候选者时，追随者与用户的位置相似度越小，追随者转发用户信息的可能性越大。

此外，考虑到追随者和用户的邻居相似性对用户信息扩散范围的影响，修改用户全局影响力的计算式为：

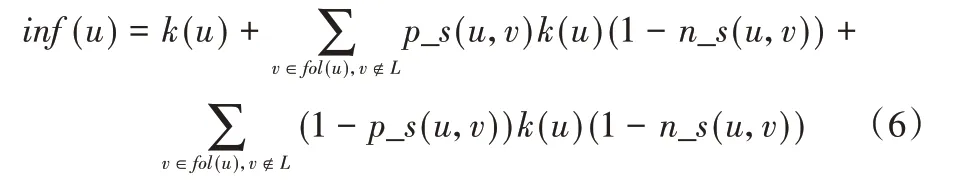
其中fol(u)是用户的追随者集合。根据上述方法，对于用户2，在意见领袖候选集L中的追随者有用户1、3、4，不在L中的追随者有用户6，如图1（c）所示，根据上述方法分别计算四位追随者的位置相似性以及邻居相似性，p_s(2，1)=0.55，n_s(2，1)=0.2，p_s(2，3)=0.7，n_s(2，3)=0.33，p_s(2，4)=0.67，n_s(2，4)=0，p_s(2，6)=0.42，n_s(2，6)=0，最终计算fol(u)=8.76。

算法1 基于K 核分解的意见领袖识别算法CandidateRank。

下面对CandidateRank 进行时间复杂度分析。CandidateRank 首先通过K 核分解得到意见领袖候选集，所以在获取所有节点K 核值时花费O(m)，其中m是网络中边的数量。后面的Sumk是所有节点K 核值之和，因此花费O(n)，n为节点个数。对于全局影响力的计算均在候选集中进行，候选集节点个数为l，通常l 远小于n，k是节点的平均度数，在位置核邻居相似性计算时时间复杂度为O(nk2)，因此CandidateRank 的时间复杂度为O(m+n+lk2)，在最坏情况下，l=n，此时时间复杂度为O(m+n(1+k2))。本文提出的算法时间复杂度高于MDD 和Cnc+算法，与ELKSS 算法复杂度相似，远小于θ 方法的O(n(n+m))，而且明显低于相关工作中提到的其他几种与K 核分解相关的方法，那些方法涉及一些中心性度量，因此时间复杂度都较高。因此，CandidateRank 在时间复杂度上有一定的优势。

4 实验与结果分析

本文实验在三个真实的数据集上进行，三个数据集分别是：1）数据集1 选取来自微博的320 个用户以及用户间的互动行为来构建出网络模型；2）数据集2 来自斯坦福公开的社交网络数据集，该数据集由来自Facebook 的“圈子”（或“好友列表”）组成。Facebook 数据是从使用这个Facebook 应用程序的调查参与者那里收集的。3）数据集3 选自微博，该数据集收集2016-12-16—2017-12-16 期间，942 740 个用户在微博平台上的关注关系和用户行为信息，这些用户之间的关注关系多达1 048 575 条。为了便于计算，本文选取其中较为活跃（有转发、发布、评论行为）的49 613 个用户构建社交网络模型。统计描述如表1 所示，数据集1、3 来自微博，数据集2来自Facebook。

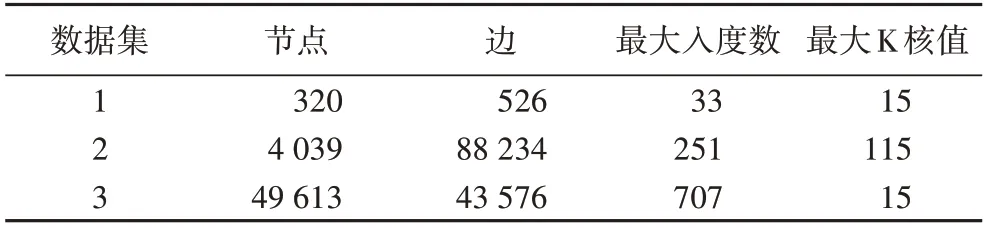
表1 实验用数据集Tab.1 Datasets for experiment

为了评估CandidateRank 算法的性能，本文将CandidateRank 算法的实验结果与其他意见领袖识别算法的实验结果进行对比，其他算法包括DegreeRank 算法、PageRank 算法、ELKSS 算法。DegreeRank 算法是度中心性算法，以网络中节点的度数来度量节点重要性。PageRank 算法根据网页间的相互链接评估网页重要度，常被用来计算用户在网络图中的重要度。ELKSS 算法是Yang 等［17］基于K-Shell改进的算法。使用两个指标来评估以上各算法的性能：基于独立级联模型（Independent Cascade Model，ICM）预测的用户影响力和基于用户中心性的用户重要度。

4.1 基于独立级联模型预测的用户影响力

本文在独立级联模型（ICM）下，使用Monte-Carlo 模拟评估各个算法所识别出的意见领袖在社交网络信息传播过程中能够影响到的用户数，表征用户影响力。假设网络中每个用户的传播概率相同，在给定传播概率后，经过实验发现Monte-Carlo 模拟次数达到10 000 次时，节点的影响范围较为稳定。同时，设置节点的传播概率p=｛0.02，0.04，0.06，0.08｝，在不同传播概率p下比较各算法所识别Top-N位意见领袖的用户影响力。在本文设定N=15，即选择每个方法所识别出的前15 个意见领袖进行评估，其结果如图3～6 所示，其中：横轴代表各算法，纵轴表示用户在给定p值下，各算法所识别的前15 位意见领袖能够影响到的用户数的统计情况。

图3 p=0.02时在三个数据集上各算法的性能Fig.3 Performance of each algorithm on three datasets with p=0.02

图4 p=0.04时在三个数据集上各算法的性能Fig.4 Performance of each algorithm on three datasets with p=0.04

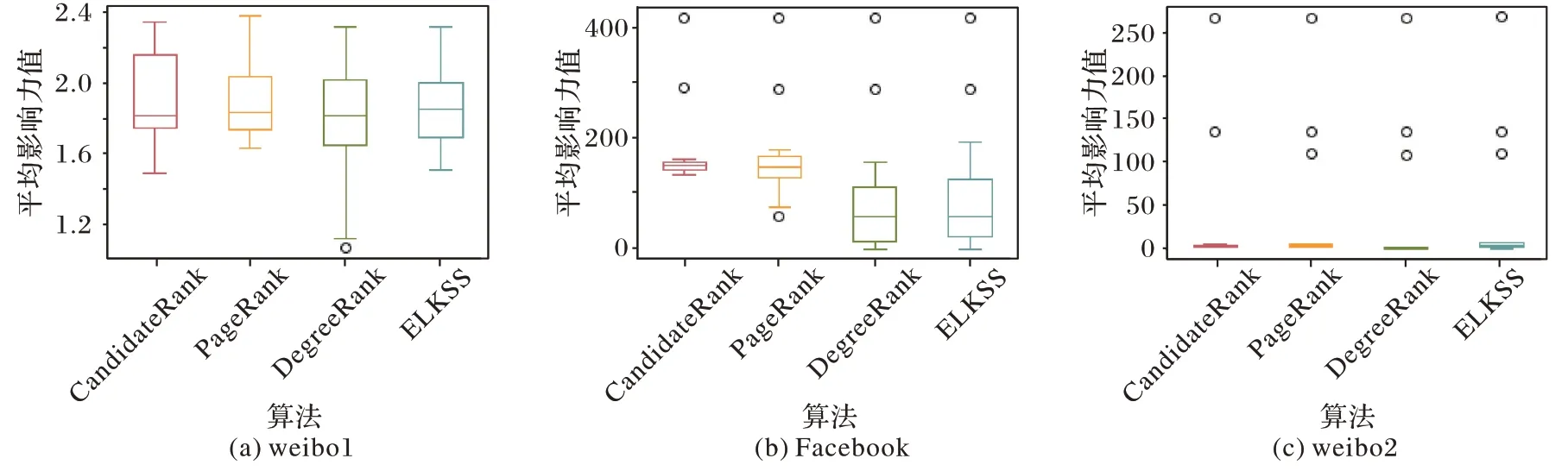
图5 p=0.06时在三个数据集上各算法的性能Fig.5 Performance of each algorithm on three datasets with p=0.06

图6 p=0.08时在三个数据集上各算法的性能Fig.6 Performance of each algorithm on three datasets with p=0.08

本文利用箱线图3～6，观察不同算法的意见领袖，在三个数据集中不同传播概率p下的用户影响力分布范围。由图3～6 可知，节点的平均影响力取值差异显著，且分布情况不同。

当p=0.02 时，在数据集1 上，四种算法得到的前15 位意见领袖影响力值（IC）的中位数十分接近，而得到的影响力最值差距较大，其中PageRank 算法得到的最大影响力均高于其他三种算法，而ELKSS 得到的最大影响力最小。DegreeRank 算法发现的意见领袖中最小用户影响力数值远远低于其他三种算法，CandidateRank 算法在该数据集上效果整体优于ELKSS 算法和DegreeRank 算法。在数据集2 中，四种算法发现的意见领袖中所具有最大用户影响力值均相同，而其他用户影响力值分布差距较大，CandidateRank 算法发现的意见领袖影响力值中位数和最小影响力值远高于其他三种算法。而在数据集3 上四种算法表现较为相似。

当p=0.04 时，由于p值的增大，在三个数据集上发现的意见领袖的影响力值均有增大。在数据集1 上，与p=0.02 不同，PageRank 算法发现的最大影响力值不是最高，而DegreeRank 算法发现的意见领袖的最大影响力值高于其他三种算法，但最小影响力值仍远低于其他算法，CandidateRank 的影响力值中位数与最小值也不低于其他三种算法，分布依然保持稳定。在数据集2 上，与p=0.02 相似，四种算法发现的意见领袖中所具有最大用户影响力值均相同，但DegreeRank 算法选出的最大影响力值低于其他三种算法较多，而CandidateRank 算法无论是最大值、中位数及最小值均高于其他算法，性能较佳。

当p=0.06 时，在数据集1 上四种算法选出的影响力值分布与p=0.02 时相似；而在数据集2 上，与p=0.04 较为不同的是，CandidateRank 算法发现的影响力值中位数不再明显高于其他方法，而是与PageRank 算法相近，但也优于其他两种算法。

当p=0.08 时，在数据集1 上，四种算法发现的意见领袖的影响力值中位数仍然保持相近，而CandidateRank 算法发现的最大影响力值高于其他算法，最小值也高于DegreeRank。在数据集2 中，本文提出的算法CandidateRank发现的影响力值中位数最高值比p=0.06 时均有所下降，但最小值依然远远高于其他算法。在数据集3 上CandidateRank 算法发现的影响力值中位数低于PageRank 算法较多，但最小值依然较高。

从图3～6 可以看出，本文提出的CandidateRank 算法在数据集1 上表现比较稳定，而且总体性能仅次于PageRank，随着p值的增加，CandidateRank 表现越来越好。而在数据集3上本文提出的算法在最高值、中位数、以及最小值方面都有很好的表现，尤其是在p=0.04 时CandidateRank 算法的性能最佳。对于数据集3，可以看到除了影响力前三的意见领袖，其他影响力值都很低，说明该数据集的意见领袖比较集中突出，在这样的特殊数据集上本文提出的算法依然能选出影响力值最大的意见领袖。

为了对比四种算法识别出的意见领袖在基于独立级联模型预测的用户影响力与其排名的关系，本文选择了一组数据进行对比，表2 为p=0.02 时在Facebook 数据集上前15 个节点的影响力值。由表2 可以发现，四种算法均识别出影响力值最大的为第一意见领袖，但PageRank、DegreeRank、ELKSS 算法识别出的其他意见领袖排名与其影响力值大小并不相符，本文提出的CandidateRank 算法识别出的意见领袖影响力值随着排名的下降而下降，从这个角度看本文提出的CandidateRank 算法性能更优。综上所述，在基于独立级联模型预测的用户影响力上，本文提出的CandidateRank 算法在不同的数据集上均能表现出优势，总体性能较好。

表2 p=0.02时在Facebook数据集上Top-15节点的影响力值Tab.2 Influence values of Top-15 nodes on Facebook dataset with p=0.02

4.2 基于用户中心性的用户重要度

在复杂网络的研究中，接近中心性、中介中心性、特征向量中心性等中心性指标能有效识别网络中的高影响力节点。因此使用包括上述3 个中心性在内的4 个中心性指标来评估各个算法所识别的意见领袖的重要度，4 个中心性指标在2.3 节中有详细介绍。在评估用户重要度时，4 个中心性指标都是中心性越大，用户重要度越大。本文选择在数据集1上对CandidateRank、PageRank、DegreeRank 和ELKSS 4 个算法所识别的前15 位意见领袖进行用户中心性计算，结果如图7 所示，4 个子图的横轴是4 种算法选出的Top-15 意见领袖排名，纵轴分别为4 个中心性值。

图7 四种算法的中心性指标值Fig.7 Centrality index values of four algorithms

从图7 的接近中心性中可以看出，随着排名数的增大，CandidateRank 算法的意见领袖在接近中心性上整体呈现下降趋势，符合排名数越靠后、重要度越小现象。而DegreeRank 算法所识别的前15 位意见领袖接近中心性的变化波动特别大，说明其性能不稳定。同时，CandidateRank 算法所识别的Top-1 意见领袖具有最大的接近中心性，因此说明CandidateRank 算法能够有效识别社交网络中的重要用户。

在中介中心性中，CandidateRank 算法和PageRank 算法的中心性变化趋势十分相似，且中心性随着排名下降的趋势比较明显，表明CandidateRank 和Page 算法在识别具有高中介中心性用户时性能较优。

在特征向量中心性和Katz 中心性中，4 种算法所识别的意见领袖的两种中心性均相似，随着排名数的增大，两种中心性波动频繁，PageRank、DegreeRank 2 种算法没有明显的随着排名而下降的趋势，而CandidateRank 和ELKSS 算法的中心性变化相对比较明显。对比CandidateRank 算法在特征向量中心性和Katz 中心性上的不同表现，可以发现CandidateRank 算法对意见领袖候选集中用户的排序更接近Katz 中心性对用户的排序。这是因为在计算用户的Katz 中心性时，与用户直接连接和间接连接的邻居被分配不同的权重，在CandidateRank 算法中，根据用户追随者身份的不同（是否属于意见领袖候选集），对追随者分配不同的权重。相较于特征向量中心性，CandidateRank 算法在Katz 中心性指标上表现更优，表明CandidateRank 算法在计算不同邻居对用户贡献的影响力时具有较高的准确性。从图7 中还可以看到，在用户中心性指标上，CandidateRank 算法的性能优于PageRank 算法和DegreeRank 算法，和ELKSS 算法的性能较为接近；但是在基于独立级联模型预测的用户影响力上，CandidateRank 算法在整体上优于ELKSS 算法。因此认为CandidateRank 算法在识别社交网络中的意见领袖时是可行的，且有效的。

4.3 相关性

4.1、4.2 节的实验反映了4 种算法识别出的最重要的意见领袖前15 位的实际影响力和中心性的情况，但是没有反映出这些节点的排序和该网络中真实传播能力较强的前15位排序的相关性，并且所对比的4 种算法中只有ELKSS 是与K 核相关的方法，因此本节仅针对与K 核相关的方法引入肯德尔相关性系数来评估算法效果，真实节点影响力还是IC模型的仿真结果。4 种算法分别是相关工作中提到的混合度分解法（MDD）、扩展近邻核，以及之前的对比方法ELKSS。表3 中列出了包括CandidateRank 方法在内的4 种意见领袖识别算法前15 位与这些节点真实传播影响力的排序之间的相关性，可以看出在2 个数据集上CandidateRank 算法的相关性都优于其他3 种算法，只有在Facebook 数据集上略低于MDD 方法，总体来看结果较优。

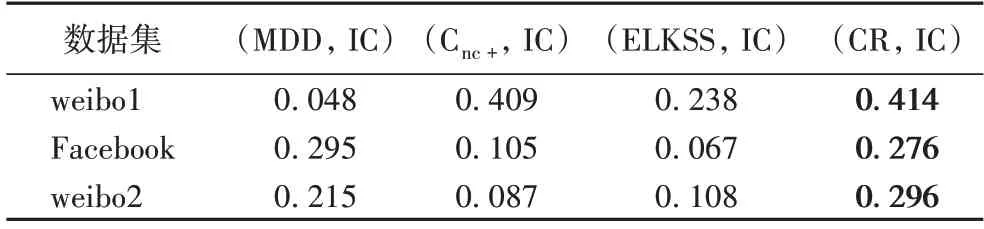
表3 四种算法计算出的意见领袖排序与真实节点影响力排序的相关性Tab.3 Correlation between ranking of opinion leaders calculated by four algorithms and ranking of influence of real nodes

5 结语

本文提出了一种社交网络中基于K 核分解的意见领袖识别算法CandidateRank。由于在社交网络中并非所有用户都有相同的机会成为意见领袖，所以通过K 核分解，选择社交网络中具有最大K 核数的用户加入到意见领袖候选集中；再根据用户的平均K 核变化率、位置相似性和邻居相似性等指标来确定用户追随者对用户影响力的贡献程度，并计算用户的全局影响力，识别意见领袖。在意见领袖候选集中确定意见领袖，一方面可以极大减少需要评估重要度的节点总数，另一方面可以增强意见领袖识别算法的适用性。在真实社交网络数据中的实验结果表明，本文提出算法是可行的，且有效的。后续研究将围绕如何使用图神经网络改进本文的算法使其在较大的网络中性能更优继续进行。