多编码树GPU并行轴心子图匹配

汪 洋，江世杰，曹宇聪，李传文

（东北大学计算机科学与工程学院，沈阳 110169）

0 引言

近年来，随着对图的重要性的认识逐渐增加，如何有效地对图数据进行管理成为了人们的研究重点。由于目前图搜索［1-3］、子图匹配等常见的图操作仍存在可扩展性和效率等方面的问题，对这些操作的研究正在受到越来越多的关注。轴心子图同构作为一种特殊的子图同构问题，也日益引起广大研究者的兴趣。对于一个给定的查询图，以查询图中的一个节点为轴心，轴心子图同构需要找到数据图中与轴心匹配的节点。所谓与轴心匹配的节点是指数据图中至少存在一个与查询图匹配的子图，子图中包含该节点。例如图1（a）为轴心子图同构的查询图Q，其轴心为u1；在图1（b）的数据图G中，v1是轴心u1的有效匹配，因为它存在于一个查询结果图中，并且位置与u1对应。

轴心子图同构的应用非常广泛，如蛋白质交互网络功能预测、频繁子图挖掘、邻居子图挖掘等［4-6］。Abdelhamid 等［7］提出了轴心子图同构算法——智能轴心子图同构（Smart Pivoted Sugraph Isomorphism，Smart PSI），利用机器学习预测候选节点是不是有效节点，从而分别利用乐观和悲观方法对该节点进行验证。在预测正确的情况下，可以根据相应算法快速求解，但是在预测错误的情况下，利用相反算法进行验证会浪费大量的计算资源和内存消耗，从而降低算法的执行效率。其他轴心子图同构算法大多先进行子图同构搜索，然后从子图同构结果中找到轴心节点。

根据算法的主要执行环境，子图同构算法可分为基于CPU 和基于GPU 两类。

基于CPU 的子图同构算法 Shang 等［8］提出了快速子图同构（Quick Subgraph Isomorphism，QuickSI），首先用快速子图同构序列（Quick subgraph Isomorphism Sequence，QISequence）来限制搜索空间，以及通过在数据库中出现的特征频数来确定序列顺序，然后用Swift index 减少过滤阶段的开 销。Han 等［9］提出涡 轮增压同构（Turbo-charged Isomorphism，TurboISO），利用查询图的查询顺序来提高子图同构算法的执行效率，同时提出邻居等价类以减少候选节点的数量，减少无用的开销。Zhang 等［10］提出了基于索引的图匹配方 法（Distance Index based subGraph mAtching，GADDI），通过在单个大图中引入频繁子结构进而提出一种距离度量方法，通过相邻判别子结构（Neighboring Discriminating Substructure，NDS）距离将一对邻居节点的局部图结构捕获，产生强大的剪枝能力。算法的执行方式［11-12］各有不同，而这些都是通过将候选节点进行过滤［13］来提高算法的执行效率。

基于GPU 的子图同构算法 随着GPU 的高速发展，研究者开始尝试将CPU 上的串行计算转化为GPU 上的并行计算。利用GPU 的多核并行处理能力，可以显著加快子图同构算法，因此许多研究人员提出了多种在GPU 上执行的子图同构算法［14-15］。例如，Bonnici 等［16］提出GRASS，通过GPU并行过滤掉当前查询节点不满足的候选节点，从而减小生成的搜索空间树的尺寸。Tran 等［17］提出的GPU 友好子图匹配（GPU-friendly Subgraph Matching，GpSM），通过生成树和访问顺序并行过滤查询节点的候选集，然后基于非树结构和约简低连接点进一步精炼候选节点，从而提高算法执行效率。GPU 友好子 图同构（GPU-friendly Subgraph Isomorphism，GSI）［18］基于与GpSM 相似的 过滤和 连接框 架，但不同 于GpSM 基于边的连接方式，GSI 采用了一种基于顶点的连接方式。

Smart PSI 虽然针对轴心子图同构进行了优化，但该方法是一种传统的基于CPU 的方法，难以有效利用GPU 等新硬件的大规模并行处理能力。为了利用GPU 的高并发能力，本文设计了一种适用于GPU 的编码过滤方式，可以并行地对候选节点进行过滤。根据查询图节点的访问顺序，该方法将下一个查询图节点的候选节点锁定在与上一个查询图节点匹配的数据图节点的邻居范围内，达到二次过滤的效果。

在过滤过程中考虑节点的特征越多，过滤的效果越好；然而选用过多的节点特征会增加过滤过程的计算量，影响总体执行效率。因此不同的过滤算法会在选用节点特征时进行一定的权衡。为了在不占用过多计算资源的同时包含更多的特征，本文提出了一种基于多编码树的过滤方法，对每个节点进行压缩编码。首先将节点的标签、度和邻居结构融入多棵不同的编码树中；然后计算每个编码树的特征向量并保存。在查询图中仅需要比较查询图节点与数据图节点的特征向量编码，即可将数据图中的无效节点进行大规模的过滤，极大缩小了候选节点生成的搜索空间树的尺寸，提高了算法的执行效率。本文提出的编码方式还充分考虑了GPU的特点，从而使GPU 在利用编码进行过滤时可以充分地进行并行操作。实验结果表明，本文方法的执行时间明显少于目前最先进的基于GPU 的子图同构算法。

本文的主要工作如下：

1）提出了一种标签树结构。利用二进制数表示图标签种类，根据各位上的数值不同，生成不同类型的标签树，从而尽可能多地展现出每个节点的邻居节点的结构特征以及邻居节点标签的组合情况。

2）提出了一种新颖的节点编码方式。将节点尽可能多的特征组合起来，利用节点的邻接矩阵的特征值来表示其邻居节点的结构和标签特征，然后将节点的标签、度以及特征值组合起来生成编码，将复杂的结构比较转化为简单的数值比较。

3）提出了一种新的轴心子图同构搜索算法。利用GPU并行过滤当前的查询图节点的候选节点，同时验证当前节点的邻居节点在已匹配序列中的位置是否是其所匹配的节点的邻居在已匹配序列中的位置的子集，将过滤与验证相结合。

1 预备知识

定义1子图同构。给定一个查询图Q={VQ，EQ，LQ}和数据图G={VG，EG，LG}，其中VQ、VG是顶点的集合，EQ、EG是边的集合，LQ、LG是将顶点映射到相应标签的标签函数。子图同构即存在一个单射函数f：VQ→VG，对于查询图Q中∀u，v∈VQ且(u，v)∈EQ，有f(u)，f(v)∈VG，(f(u)，f(v))∈EG，LQ(u)=LG(f(u))且LQ(v)=LG(f(v))。

定义2轴心子图同构。给定一个查询图Q={VQ，EQ，LQ}，轴心up∈VQ以及数据图G={VG，EG，LG}，轴心vp∈VG，存在一个单射函数f：VQ→VG，轴心子图同构需要满足如下三个条件：1）∀u，v∈VQ有f(u)，f(v)∈VG，LQ(u)=LG(f(u)) 且LQ(v)=LG(f(v))；2）∀(u，v)∈EQ，有(f(u)，f(v))∈EG；3）vp=f(up)。

轴心子图同构问题类似于子图同构问题，但是轴心子图同构问题不需要在数据图中找到所有与查询图匹配的子图，而只需要在数据图中找到所有与查询图轴心匹配的节点，每一节点至少存在于一个与查询图子图同构的子图中。与子图同构相比，轴心子图同构只需要少量的计算和内存。如图1 所示，轴心子图同构的结果为{v1}，不包括v5，这是因为v1存在子图(v1，v2，v3，v4)与查询图匹配，而v5不存在与查询图匹配的子图。

定义3诱导子图。一个诱导子图g是图G的节点的子集以及这些节点子集在G中形成的边。

定理1［19］给定树T有n个顶点和树T′有m个顶点(n≥m)，它们的邻接矩阵分别记为A和B。对于矩阵A，其特征值为λ1≥λ2≥…λn。对于矩 阵B，其特征值为α1≥α2≥…αm。如果T′是T的一个诱导子树，则λn-m+i≤αi≤λi(i=1，2，…，m)。

定理1 是树与其诱导子树的邻接矩阵特征值之间的关系。本文中，将图转化为树，利用定理1 验证子图。但是需要注意的是，定理1 只是一个必要条件而不是一个充分必要条件，对于满足上述特征值条件的图S和图G，无法得到图G是图S的一个诱导子图或者是子图，但是可以得到满足上述条件的图一定包含了图S的所有子图。因此可以利用此条件进行过滤，依据查询图节点邻居结构，对数据图中每个节点邻居结构不满足上述条件的节点进行剪枝。

2 总体结构

本文提出了一种基于GPU 的轴心子图同构算法，由编码过滤、二次过滤和验证两阶段构成。

2.1 编码过滤

过滤阶段着重研究如何将节点的邻居结构以及节点的邻居标签应用到编码中，从而过滤掉更多候选节点。对于查询图节点的候选节点来说，除了其本身的特征满足查询节点特征外，其邻居节点的特征也要满足查询节点的邻居特征。邻居结构是邻居特征的重要因素，本文利用邻接矩阵来表示。由于定理1 只适用于树结构，因此本文将图节点的邻居结构转化为树结构。如果查询图节点的邻居结构不是其候选节点邻居结构的子结构，那么通过定理1 可以过滤掉该候选节点。

本文通过标签编码树的方式将邻居节点标签应用到邻居结构上，以增强过滤能力。事实上，每个节点都可以根据其邻居结构生成一棵无标签树。然而邻居节点的标签可能不同，仅生成无标签树无法进行有效的比较。因此本文根据标签类型对树进行切割，将同一类标签的节点放到一棵树中。

定理2对于树T′和T，按照将相同标签的节点放入同种标签树中的规则将其切割成n个子树，得到子树序列和ST={t1，t2，…，ti，…，tn}，如 果序列中的所有ti′都是ti的诱导子树，那么T′一定是T的一个诱导子树。

证明 由于标签加入，若序列中的所有都是ti的诱导子树，那么去掉标签后所有依旧是ti的诱导子树，则T′必然是T的诱导子树。

标签树将原本的无标签树按照同标签组合原则进行分割，加强了过滤条件，使其不仅需要满足结构特征也要满足标签特征。由于对于每个节点的切割规则是相同的，所以每个节点所产生树的数目相同，在比较时通过对应的标签树的特征值进行比较，即可过滤掉不满足的节点。

2.2 过滤和验证

二次过滤和验证是利用过滤与验证框架，将编码过滤后得到的每个查询图节点的候选集再次过滤。这次过滤是依据轴心子图同构的第二个条件，即如果两个查询图节点之间存在边，那么它们在数据图中的候选节点之间也必定存在边，否则该节点即可被过滤掉。

对于两个候选节点之间是否存在边这一条件，可以利用访问顺序解决，而不需要验证边的存在：给定查询图，从查询图的轴心节点开始，依次访问轴心节点的邻居，那么在数据图中就会依次访问轴心候选节点的邻居，无需访问非邻居节点。

最后，需要验证得到的子图是否和查询图符合子图同构的条件。总体的过滤和验证过程将在第4 章详细介绍。

3 多编码树过滤

尽可能多地过滤掉查询图节点的候选节点是提高算法的执行效率的有效途径。对于无向图而言，节点的标签和度是现有的许多编码方式［20］都会利用的特征。但是对于大图而言，这种编码方式的过滤能力并不显著。因此将节点的邻居结构组合到编码中引起了很多人的研究兴趣，然而如何在编码邻居结构的同时保持编码结果的简洁高效始终是一个难点问题。本文利用节点的邻居结构特征，将邻居节点的标签融入多编码树的特征值中，将复杂的结构特征比较转化为数值之间的比较，从而简化了邻居结构编码，缩短了过滤过程的执行时间。

编码分为两个部分，首先根据节点邻居的结构特征，对节点周围的邻居生成一棵固定层数的树；其次是结合节点邻居的标签，将节点的一棵树分割成多棵树。3.1 节和3.2 节将详细介绍这两部分内容。基于这两部分的实现，本文方法将数据图的节点与查询图的节点进行编码，得到查询图每个节点的候选节点。

算法1 生成n层无标签树。

3.1 邻居结构特征

对于图的每个节点，可根据其邻居节点的结构生成一棵固定层数的树，节点本身作为根节点。算法1 展示了图G中顶点v构造成n层树的步骤，以当前节点为根，采用广度优先遍历将其邻居节点插入到树中，生成n层树。首先需要将当前节点的邻居节点插入到树中作为根的孩子，并标记为已访问（4）行～5）行）。之后对当前节点的每个邻居节点各自执行search 函数（6）行）生成多棵当前节点的子树，search 函数是一个递归函数，作用是将当前节点的未被访问过的邻居节点作为孩子插入树中（9）行～19）行），直到树的层数达到设定值（10）行）。

以图2 为例，图中对于图1 中给定查询图Q和数据图G，分别以u1和v1、v5为根节点生成一个2层的树结构。通过验证查询图节点生成的n层树是否是数据图节点生成的n层树的子树，来过滤掉不满足的节点。因此本文可以利用邻接矩阵表示n层树结构，对于n阶矩阵存在n个特征值，GCoding（Graph Coding）［19］中对前2、3个，n个最大特征值进行了实验，实验结果表明选择前2 个最大特征值性能更优。因此本文也选取邻接矩阵的前2个最大特征值，即利用2个简单的数值来表示复杂的邻居结构。

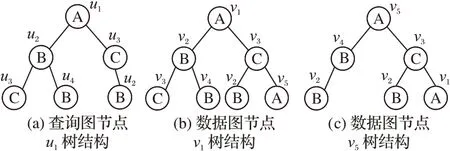
图2 查询节点u1和数据节点v1、v5生成的2层树结构Fig.2 Two-level tree structures generated by query node u1 and data nodes v1，v5

3.2 邻居标签特征

如果将给定图中的每个顶点都根据算法1 生成一棵树，将过滤掉数据图中与查询图节点邻居结构不一致的节点。然而这种做法只考虑了邻居结构问题，而没有充分利用邻居的标签信息。想要高效地过滤节点必须尽可能多地考虑节点以及节点邻居的标签特征。

上述问题带来以下两个挑战：

1）每个节点的邻居标签各不相同，将节点标签所有的可能情况排列组合，标签树的总量必将过于庞大而难以实用。

2）如果对于每个顶点所生成的树根据标签的类型进行分割，将每种标签的邻居节点组合生成一棵树，这样生成的标签树内容单一且数量不确定。这是因为每个顶点周围的邻居标签有几类就会生成几棵树，并且对于数据图标签种类较多的情况生成树的数量会更多，难以编码。

面对以上挑战，本文提出了一种多标签的编码树方式：用二进制数来表示标签，如果图中共有n种标签，则可以设置不超过n个标签桶，将每种标签按一定形式（哈希、等分等）归入一个标签桶中，每个标签桶按顺序从1 开始编号。然后将标签桶序号二进制形式第i位为1 的所有标签桶归为第i组，共有组。同一个标签桶组的所有标签类型的邻居节点将被用来生成同一棵树。

例如，在一个包含30 种标签的图中，最多可以生成30 个标签桶，进而产生=5 个标签桶组，每个标签桶组生成一棵树，最终每个节点可生成5 棵树。除此之外，本文还生成1 棵由算法1 所生成的不考虑邻居节点标签的树。

然而，对于给定的n种标签，也可以生成少于n个标签桶。具体生成多少标签桶将参照实验结果进行讨论。表1给出了30 个标签哈希到3 个标签桶中生成2 棵树的情况，其中桶ID 由1～3 表示，每个桶ID 由两位二进制数表示，根据每个节点标签所在的桶ID 的各个位置上是否为1 分成相应的标签桶组，两位二进制数可以分成两个标签桶组（只考虑各个位置为1 的情况），因此可以生成2 棵树。

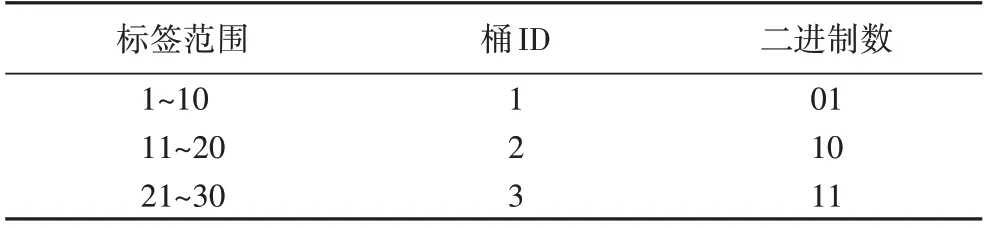
表1 30个标签哈希到标签桶中生成2棵树Tab.1 Thirty labels hashing into label buckets to generate 2 trees

虽然编码节点本身在生成树的时候不考虑节点标签，但由于节点本身的标签和度会单独进行编码，因此这样做并不会影响过滤效果。在进行比较操作时，只需对同类型的树得到的特征值相互比较，因此可以实现较高的过滤效率。采用这种方式对树进行切割，包含了所有标签的可能情况，并且每一棵树都能覆盖到图中一半的标签，增强了过滤效果。

算法2 生成同类标签树。

算法2 描述了标签树的生成过程：以当前节点为根，采用深度优先遍历的方式将其邻居节点插入到满足条件的多棵标签树中，从而生成多个n层标签树。依据算法1 生成一棵无标签树，然后保持根节点不变生成多棵标签树（1）行～3）行），之后递归遍历无标签树（4）行），根据flag确定节点属于哪棵标签树（11）行～14）行）。通过findAncestors 函数找到与目前节点相连的父节点，如果父节点不存在，则继续向上查找直到根节点。

图3 给出了本文方法的一个示例。根据图1 中标签类型，将各种标签哈希到相应的桶中，并根据相应的桶ID 来确定标签树。由图3 可见，轴心u1和候选节点v1具有相近的邻居结构，而与v5的邻居结构差异则较大。图节点的每棵树都要转化为邻接矩阵并求其特征值，选择前两个最大的特征值作为特征进行编码。本文方法将顶点的标签、度以及顶点邻居生成的标签树的特征值组合起来表示为Tcoding={label，degree，seq={a1，a2，b1，b2，…}}。编码可 以采用脱机处理的方式进行预计算。

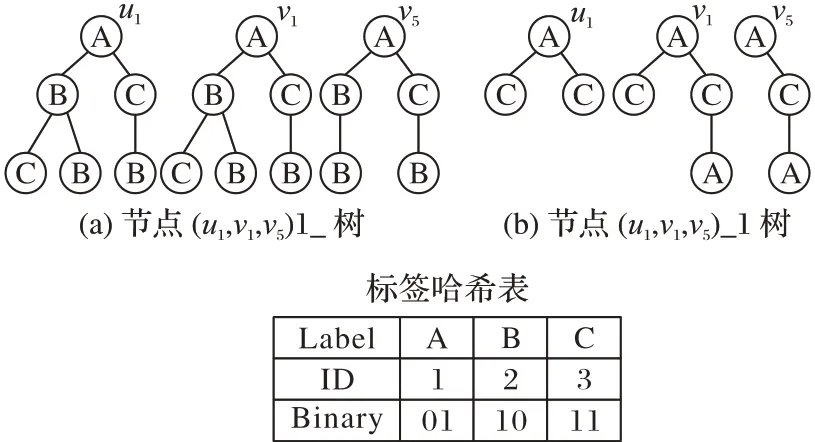
图3 查询节点u1和数据节点v1，v5生成的标签树Fig.3 Label trees generated by query node u1 and data nodes v1，v5

对于查询图中的每一个节点的多标签树，在过滤过程中将其前两个最大特征值与数据图中节点的多标签树特征值进行比较。当数据图中的节点的顶点编码与查询图的节点的顶点编码符合如下条件才可以被存入查询图节点的候选集：1）节点标签必须相同；2）查询图节点的度必须小于等于数据图节点的度；3）查询图节点生成的每棵标签树对应的特征值必须小于等于数据图节点生成的每棵标签树对应的特征值。

算法3 编码过滤。

算法3 给出了编码过滤的过程。首先初始化查询图节点的候选集（1）行～3）行）；其次按照查询图节点访问顺序依次访问，每个查询图节点与数据图节点并行比较编码，将符合条件的数据图节点存入候选集（4）行～10）行）。GPU 中的并行处理方式是以线程束为单位，每个线程束包含的32 个线程内部以并行方式同时处理一个查询图节点与32 个数据图节点之间的比较操作，过滤掉不满足的数据图节点，并将过滤结果合并存储。这种高效的编码过滤过程很大程度上减少了过滤所需的时间。图4 给出了查询图Q和数据图G每个节点的编码，依据上述条件进行比较可以得到过滤后的每个查询图节点的候选集分别为u1={v1}，u2={v2}，u3={v3}，u4={v2，v4}。

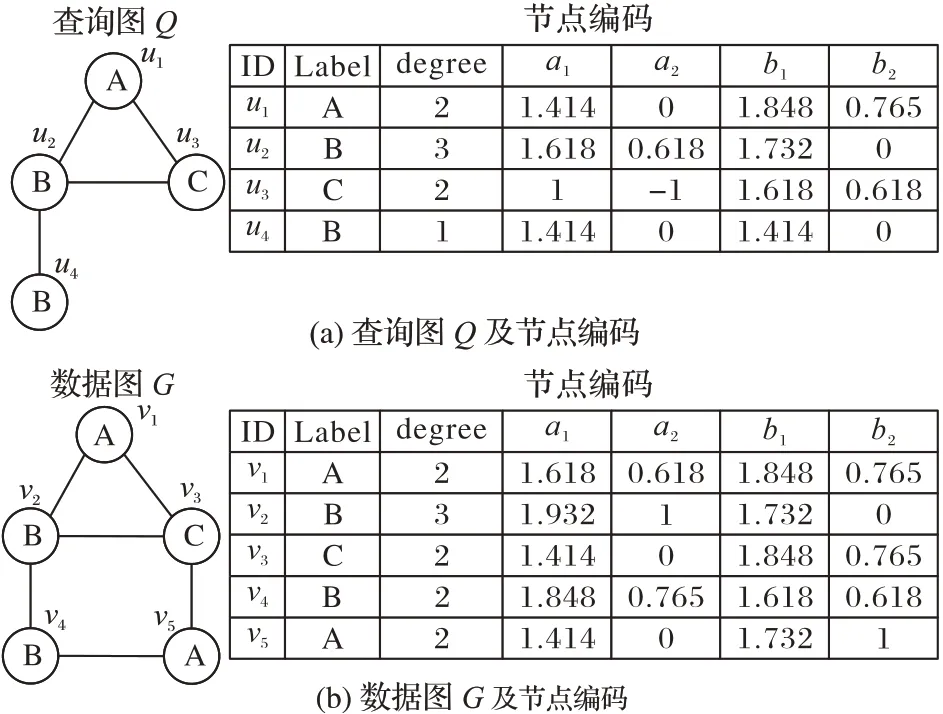
图4 查询图Q与数据图G的节点编码Fig.4 Node coding of query graph Q and data graph G

4 二次过滤和验证

4.1 过滤规则

给定查询图Q和数据图G以及查询图节点的访问顺序，以查询图轴心为起始节点，依次访问轴心的邻居，数据图中同样以轴心候选节点为起始节点，依次访问邻居节点，这样就可以直接过滤掉与轴心候选节点之间不存在边的候选节点，同样地，随后每一层的节点都必须是上一层已匹配节点的邻居。

4.2 验证规则

给定查询图Q和数据图G，将已匹配的查询图节点ui以及其在数据图中的匹配节点vi存入匹配序列seq={(u1，v1)，(u2，v2)，…，(ui，vi)，…}。将当前查询图节点的邻居在匹配序列中的位置存入集合SQ中，并将其匹配的数据图的节点的邻居在匹配序列中的位置存入集合SG中，匹配过程中必须满足SQ是SG的子集。

每个查询图节点得到的候选集都可以生成一棵搜索空间树，每一层都是查询图节点的候选集。遍历搜索空间树的过程中，本文方法将剪枝和验证过程相结合，分别从查询图轴心和其在数据图中的候选节点开始，按照邻居节点顺序依次访问。对于每个查询图节点的候选集，根据过滤规则必须是当前查询图节点的被访问过的父节点的邻居。本文利用GPU 并行剪枝掉不满足的节点，同时根据验证规则对已匹配序列中当前查询节点邻居的位置进行验证。验证采用深度优先遍历的方式，直到所有查询图节点均被访问过，如果得到一个查询图的有效匹配，则轴心的这个候选节点就是轴心子图同构的解之一。将轴心的候选节点依次验证，最终得到轴心的所有匹配。图5 给出了单个轴心候选节点的验证过程。对于单个轴心候选节点，依据过滤规则将下一层中所有不是其邻居的候选节点过滤掉，再在这一层中选择剩余候选节点中的一个节点继续往下一层进行过滤，其中每一层都进行了并行剪枝，并对剪枝后的候选节点进行验证。如果某一层的一个节点不满足验证规则，转而寻找该层的下一个节点继续进行验证，直至最后一层，仍然有满足验证规则的节点，则得到了一个有效的子图匹配。如果某一层的所有节点都无法满足验证规则，那么无法得到查询图的有效匹配，则此轴心候选节点为无效节点。

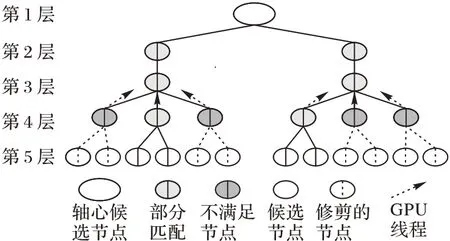
图5 单个轴心候选节点的验证过程Fig.5 Validation process of one pivoted candidate node

5 实验结果

本章通过实验对本文提出的算法进行性能分析。由于目前唯一的针对轴心子图同构进行了优化的Smart PSI 是一种传统的基于CPU 的方法，难以有效利用GPU 等新硬件的大规模并行处理能力。实验中将目前最先进的基于GPU 的子图同构算法GpSM 与本文算法进行比较。

本文选用了两个有着不同的结构和尺寸的真实数据集，其中Human 数据集［21］包含4 674 个节点、86 282 个边以及44种节点标签，Hprd 数据集［21］包含9 460 个节点、34 998 个边以及307 种节点标签。显然Human 数据集是一个稠密数据集，每个节点连接约19 条边；而Hprd 数据集是一个稀疏数据集，每个节点连接约4 条边。在实验测试中使用的都是无向图，且这两个数据集均没有边标签。

本文在数据图中随机选择一系列连通子图作为查询图，并且随机选择其中的一个节点为轴心。由于Human 数据集是稠密数据集，本文将查询图的尺寸指定为4、8、12、16、20个节点，对于Hprd 数据集，指定查询图的尺寸为8、16、24、32个节点。

所有代码都由C++实现，运行在CUDA Toolkit 10.6、NVIDIA GeForce 940MX GPU 上。

5.1 k的影响

图6 给出了在Human 数据集中不同棵树的过滤能力的实验结果。Human 有44 种标签，最多能够生成6 棵标签树，每棵标签树都是在生成2 层树的前提下执行的。无论查询图的尺寸大小，在6 棵树的情况下所能过滤的候选节点更多。这是因为6 棵标签树可以包含数据图中的所有标签种类，产生更多的过滤条件。而只有1 棵树则过于单调，只考虑节点邻居结构没有考虑节点邻居标签信息。其他的树均没有充分利用节点邻居标签和结构，因此得到的过滤效果比6 棵树较差。

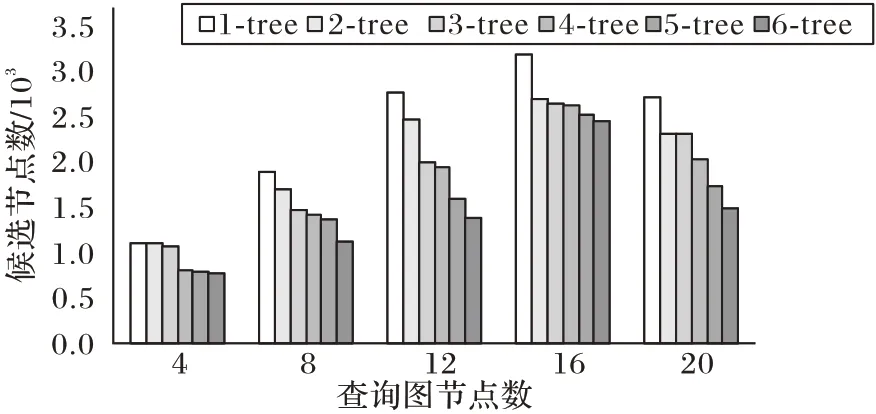
图6 不同棵树在Human数据集上对于候选节点的过滤能力Fig.6 Filtering ability to candidate nodes with different tree numbers on Human dataset

5.2 和GpSM比较

本文通过实验来比较轴心子图同构算法与GpSM 算法的性能，对于不同的查询图尺寸和不同的数据图尺寸（Human 和Hprd 数据集中固定查询图尺寸分别为12、16）分别给出了两个算法的实验结果。

本文将性能比较分为三个方面，分别为过滤能力、过滤时间以及整个算法执行时间。图7（a）给出了在查询图尺寸为4、8、12、16、20 的情况下在Human 数据集中的候选节点的个数。轴心子图同构算法的过滤效果随着查询图尺寸增加趋于稳定，与GpSM 保持着较小的差距。其中12-tree 是前文中提到的在6-tree 上所做的扩展，其性能有较小的提升。图7（b）给出了在数据图尺寸为1 000、2 000、3 000、4 000、5 000的情况下在Human 数据集中的候选节点的个数。随着数据集尺寸的增大，轴心子图同构算法的过滤效果依然趋于稳定，没有增大与GpSM 算法过滤效果的差距。

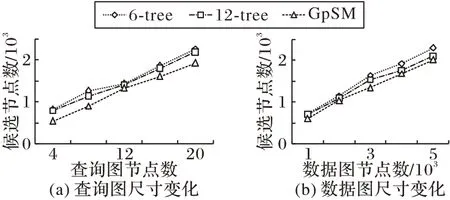
图7 Human数据集上过滤后的候选节点Fig.7 Filtered candidate nodes on Human dataset

图8（a）给出了在查询图尺寸为4、8、12、16、20 的情况下在Human 数据集上的过滤时间。图8（b）给出了在查询图尺寸为8、16、24、32 的情况下在Hprd 数据集上的过滤时间。随着查询图尺寸的增大，轴心子图同构算法的过滤时间几乎没有增长，而GpSM 算法的过滤时间大幅增加。这是因为轴心子图同构算法中的过滤阶段是通过GPU 并行处理每一个查询节点，并且过滤使用的编码是简单的数值比较，所以过滤的时间消耗相对较少，并且不会有太大的变化。而GpSM 算法是通过构建查询图的最小生成树，随着查询图尺寸的增加，构建的最小生成树便随着增大，且时间消耗也会随之增加。同样的，12-tree 是6-tree 的扩展，其过滤时间和6-tree 的过滤时间相差无几。图8（c）展现了数据图尺寸为1 000、2 000、3 000、4 000、5 000 的情况下在Human 数据集上轴心子图同构算法的过滤时间。图8（d）展现了数据图尺寸为2 000、4 000、6 000、8 000、10 000 的情况下在Hprd 数据集上轴心子图同构算法的过滤时间。随着数据集尺寸的增大，轴心子图同构算法的过滤时间只有小幅的增长，而GpSM 算法的过滤时间有着相对大幅的增加。数据集的尺寸大小会影响查询图中每个节点过滤所需的时间，并且当数据集的尺寸逐渐增大时，GpSM 通过最小生成树的访问顺序过滤后得到的候选集尺寸增大，从而影响过滤时间。

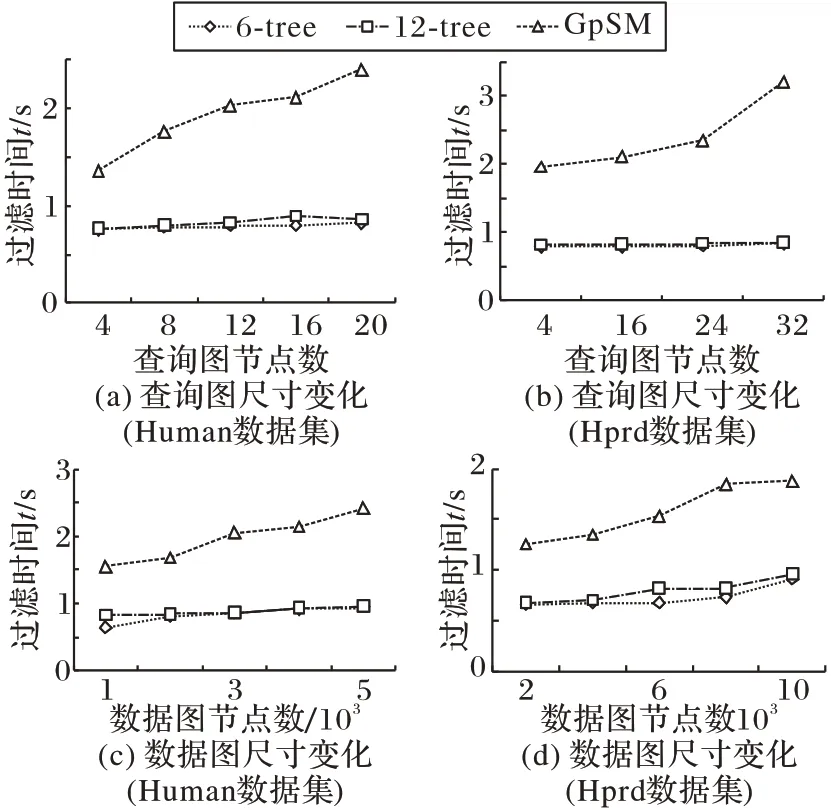
图8 不同数据集上算法的过滤时间Fig.8 Filtering time of algorithms on different datasets

图9（a）给出了在查询图尺寸为4、8、12、16、20 的情况下在Human 数据集上的整个算法执行时间。图9（b）给出了在查询图尺寸为8、16、24、32 的情况下，在Hprd 数据集上的整个算法执行时间。随着查询图尺寸的增加，GpSM 算法执行时间呈线性增长，而轴心子图同构算法的执行时间是先相对平稳再趋于线性增长，但总体时间要少于GpSM 算法。这是因为与轴心子图同构算法相比，GpSM 算法的过滤和连接都要低效，连接过程需要将边的候选节点选出并存入哈希表中，而这是非常耗时的。图9（c）给出了数据图尺寸为1 000、2 000、3 000、4 000、5 000 的情况下在Human 数据集上轴心子图同构算法执行的总时间。图9（d）给出了数据图尺寸为2 000、4 000、6 000、8 000、10 000 的情况下在Hprd 数据集上轴心子图同构算法执行的总时间。随着数据集尺寸的增加，算法耗时都趋于线性增长。这是因为数据集尺寸的增加会增大GpSM 算法过滤后得到的候选集尺寸，间接增大了连接阶段的边的候选集的尺寸，使得边的候选集存入哈希表的时间也会相应增加，影响了算法的执行时间。

图9 不同数据集上的算法执行总时间Fig.9 Total execution time of algorithms on different datasets

6 结语

本文提出了一种新颖的多编码树过滤方式，将邻居结构和邻居节点标签转化为多个包含标签信息的编码树，用特征值表示标签树的结构，结合节点特征以及不同标签树的特征值得到每个节点的编码；通过GPU 并行比较每个查询节点与数据节点的编码进行过滤，减小了轴心子图同构算法生成的搜索空间树的规模。在此基础上，本文提出了轴心子图同构算法，结合过滤和验证方式，并行处理每个查询节点由多编码树过滤后的候选节点，验证子图是否是查询图的有效匹配，最终得到轴心的所有有效匹配节点。实验结果表明本文算法在过滤效果上相对稳定且与GpSM 有着较小的差距，在过滤时间和算法总体时间上要优于当前最先进的基于GPU的GpSM 算法。