基于动态相关性的特征选择算法

陈永波，李巧勤，刘勇国

（电子科技大学信息与软件工程学院，成都 610054）

0 引言

特征选择可以从高维数据中抽取相关特征，剔除无关和冗余特征，减小数据维度，缩短数据处理和模型训练的时间。按照特征选择过程与分类算法的不同结合方式，可分为封装式、嵌入式和过滤式。封装式特征选择结合某特定分类算法，根据分类算法的分类结果以度量特征重要性。此类方法在特征选择过程中与后续分类算法相结合，所以选择的特征子集较好。但该方法效率较低，每次选择特征时均要执行分类算法以判断特征子集优劣。嵌入式特征选择是将特征选择过程作为分类算法的一部分，在学习和优化算法的过程中，自动地完成特征选择。如决策树分类算法通过持续寻找最优特征，使用最优特征将数据集进行划分，当数据集不可再分或无法选择最优特征时，算法结束并完成特征选择［1］。此类方法避免每次添加新特征时对模型进行训练，但较难构建优化模型。过滤式特征选择独立于分类算法，不使用分类算法的分类结果去评估某个特征，通过评价函数对数据进行特征选择。相较于前两类方法，此类方法不依赖任何分类算法，易于理解，简单高效。过滤式特征选择常见的评价函数包括距离度量、依赖性度量、信息度量等。距离度量评价样本间距离，距离越小，样本间相似度越高，越可能同属于一个类别。依赖性度量评价特征与特征或类别与特征间的相关性，与类别相关性大的特征，被认为是好特征。信息度量常用互信息评价特征的优劣，特征与类别的互信息越大，特征与类别相关性越高。互信息的理论基础是信息熵，可以有效地评估变量之间的关系，经常作为过滤式特征选择的评价函数；然而基于互信息的传统过滤式特征选择，没有在特征选择过程中，探究已选特征与类别的动态变化，可能会造成候选特征的错误选择。针对此类情况，Gao 等［2］提出已选特征和类别动态变化（Dynamic Change of Selected Feature with the class，DCSF）算法，算法使用条件互信息，计算已选特征和类别间信息量的动态变化。但DCSF 算法在特征选择过程中，没有同时度量候选特征、已选特征、类别间关系，即交互相关性，造成特征与类别的相关性计算不够精准，导致特征选择的分类准确率低。

针对DCSF 算法存在的问题，本文提出基于动态相关性的特征选择（Dynamic Relevance based Feature Selection，DRFS）算法，利用条件互信息，衡量已选特征/候选特征出现的条件下，候选特征/已选特征和类别的条件相关性，利用交互信息，衡量候选特征-已选特征-类别的交互相关性，以提升特征选择的分类准确率。实验结果表明，本文所提算法优于对比特征选择算法，验证了算法有效性。

1 相关理论

1.1 信息熵

信息理论提供评估随机变量信息的方法，信息熵用于评估随机变量不确定程度［3-4］。给定离散型随机变量X=｛x1，x2，…，xn｝，xi的概率用p（xi）表示，信息熵H（X）定义如式（1）：

给定离散型随机变量Y={y1，y2，…，ym}，p(xi，yj)表示X和Y的联合概率，其中i=1，2，…，n，j=1，2，…，m。联合熵H(X，Y)表示X和Y同时出现时的信息量，定义如式（2）：

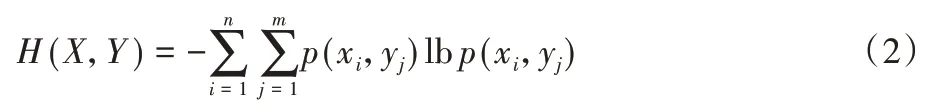
在Y已知的条件下，X的不确定程度由条件熵度量。设p(xi|yj)表示条件概率，条件熵H(X|Y)的定义如式（3）：

1.2 互信息

互信息I(X；Y) 可衡量X和Y的独立程度，定义如式（4）：

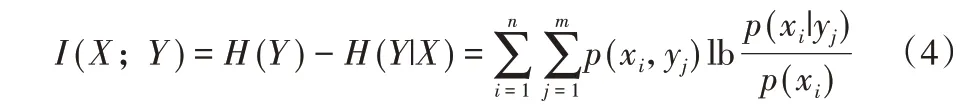
由式（4）可知，互信息I(X；Y)可等价为给定X的条件下，Y的不确定程度的减少量。如果X可以确定Y，则I(X；Y)的值为H(Y)。如果X和Y无关，即H(Y|X)=H(Y)，则I(X；Y)的值为0。

设Z={z1，z2，…，zk}为离散型随机变量，条件互信息I(X；Y|Z)表示给定Z，由于Y的加入，X的不确定程度的减少量，定义如式（5）：

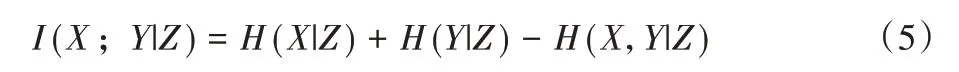
其中H(X|Y，Z)是条件熵，表示给定Y和Z条件下，X的不确定程度。联合互信息I(X，Y；Z)定义如式（6）：

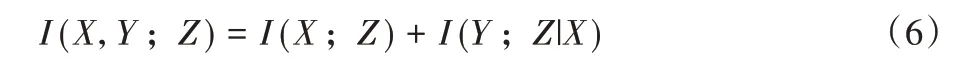
互信息可度量变量之间双向相互作用。对于变量X、Y、Z间相互作用，由交互信息I(X；Y；Z) 度 量，定 义［5］如式（7）：

I(X；Y；Z) ＞0 时，表示X和Y发挥协同作用，提供X或者Y单独存在时不能够提供的信息；I(X；Y；Z) ＜0 时，表明它们提供相同的信息；I(X；Y；Z)=0 时，表示Y(X)的加入，不影响X(Y)与Z的关系。

2 相关工作

基于互信息的过滤式特征选择，因其易于理解、过程简单、计算复杂度低等优点，得到广泛研究［6］。互信息最大化（Mutual Information Maximization，MIM）算法［7］根据候选特征和类别间的互信息值大小，对特征的重要性进行排序，完成特征子集的选择，评价函数如式（8）：

其中：Fm表示候选特征，C表示类别。MIM 算法虽然考虑特征相关性，获得类别相关的特征，但是没有考虑候选特征和已选特征之间的冗余性，即特征冗余性。良好的候选特征与类别高度相关，而且可以提供已选特征无法提供的信息。

为了弥补MIM 算法的不足，Battiti［8］提出互信息特征选择（Mutual Information Feature Selection，MIFS）算法，评价函数如式（9）：

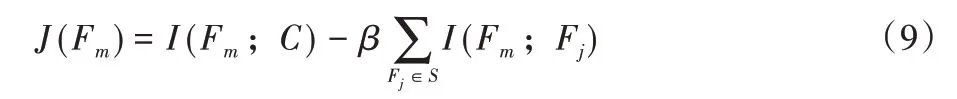
其中：Fj表示已选特征，S表示已选特征集合，β∈[0，1]是调节特征相关性和特征冗余性的平衡参数。MIFS 算法第一部分是特征相关性I(Fm；C)，第二部分是特征冗余性I(Fm；Fj)。MIFS 评价函数的第二项是累加项，随着S的增大，冗余信息不断增大，去除冗余特征和选择相关特征变得困难。针对此问题，Peng 等［9］提出最小冗余性最大相关性（minimal-Redundancy-Maximal-Relevance，mRMR）算法，评价函数如式（10）：

mRMR 与MIFS 的评价函数相似，两者不同之处是平衡参数，mRMR 算法使用已选特征集合基数的倒数，避免随着已选特征数量增加，冗余信息不断增大的问题。

Yang 等［10］提出基 于联合 互信息（Joint Mutual Information，JMI）算法。该算法认为候选特征和已选特征具有交互性，评价函数如式（11）：

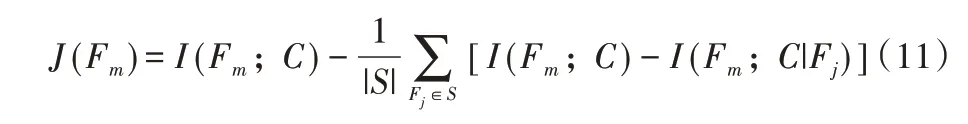
由式（11）可知，JMI 算法使用I(Fm；C|Fj)-I(Fm；C)=I(Fm；C；Fj)度量特征交互性。

3 已选特征和类别动态变化算法

现有基于互信息的特征评价函数，忽略了已选特征是动态变化的，只关注候选特征和类别的相关性，没有思考已选特征和类别的相关性，致使无法区分候选特征的重要性，如表1 和2［11］所示。

表1 中假设F1为已选择特征，F2和F3为候选特征，C为类别；表2 分别计算上述特征与类别间互信息、条件互信息以及联合互信息。由表2 可 知，I(F1；C|F2)＜I(F1；C)，I(F1；C|F3)＞I(F1；C)，选择特征F1后，给出候选特征F2和F3，已选特征F1和类别间的信息量是不同的，说明加入候选特征，会导致已选特征与类别的互信息发生变化，故需揭示信息量变化以评价候选特征。

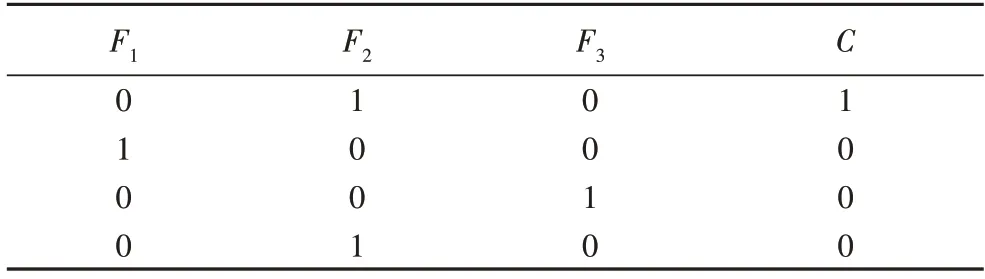
表1 人工数据集Tab.1 Artificial dataset

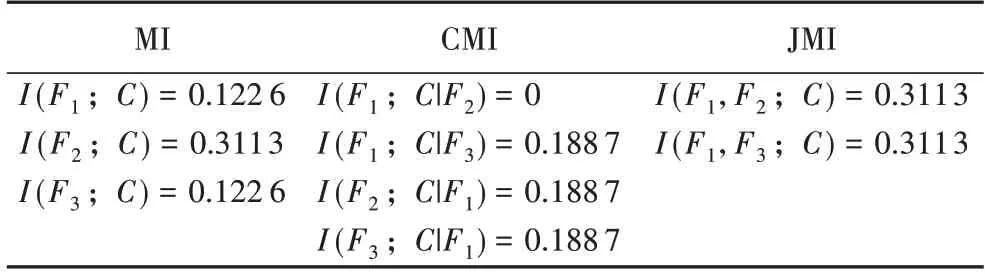
表2 特征和类别之间的信息量Tab.2 Amount of information between feature and class

针对以上情况，Gao 等［2］在2018 年提出已选特征和类别动态变化（DCSF）算法，评价函数如式（12）：

其中：I(Fm；C|Fj)表示在已选特征Fj出现的条件下，候选特征Fm和类别C的相关性；I(Fj；C|Fm)表示在候选特征Fm出现的条件下，已选特征Fj和类别C的相关性；I(Fm；Fj)评估特征的冗余性。DCSF 算法基于条件互信息，在特征选择过程中，度量已选特征和类别之间动态变化的信息量。

4 动态相关性特征选择算法

DCSF 算法虽然考虑了已选特征和类别的动态变化，但忽略了交互相关性，对候选特征、已选特征、类别间相关性计算不精确，造成特征选择分类准确率不足。图1 展示了DCSF 算法存在的问题。

可见，候选特征Fm的信息量包括：1）已选特征Fj出现，候选特征Fm提供的额外信息量，表示为I(Fm；C|Fj)，即图1中的第2 部分；2）候选特征Fm出现，提供的额外信息量，表示为I(Fj；C|Fm)，即图1 中的第3 部分。候选特征Fm的加入，不仅提供了与类别相关的信息量，也提供了冗余的信息量，表示为I(Fm；Fj)。可见，DCSF 算法用条件相关性度量候选特征Fm提供的相关信息，特征冗余性度量候选特征Fm带来的冗余信息。

由图1 可知，I(Fm；Fj)包含的信息有第1 部分交互信息和第4 部分类外冗余信息。其中第4 部分是类外冗余信息，与类别无关，无法提供与类别相关的信息［12］。第1 部分是交互信息，候选特征Fm和已选特征Fj可能产生交互性相关性，发挥正向协同作用，提供与类别有关的信息［5］。

图1 特征与类别的关系Fig.1 Relationship between feature and class

由上述可知，DCSF 算法在特征选择过程中，虽考虑了已选特征和类别的动态变化信息量，但忽略了交互相关性，对特征与类别的相关性计算不够精准。针对DCSF 算法存在的上述问题，本文提出基于动态相关性的特征选择（DRFS）算法，评价函数如式（13）：

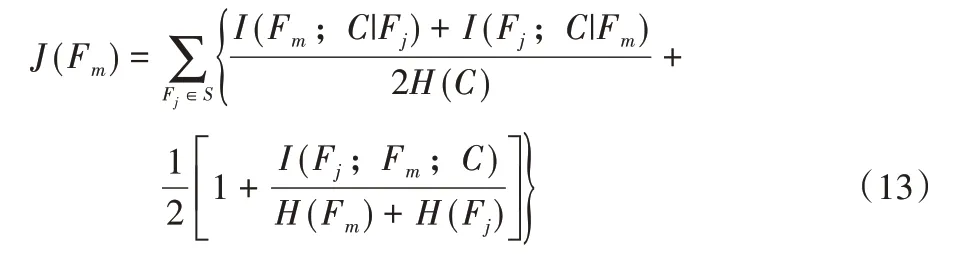
评价函数第一项的I(Fj；C|Fm)，度量已选特征Fj和类别C的信息量，随候选特征Fm的出现，所发生的动态变化。出现式（14）的情形：

表示已选特征和候选特征不分享共同的信息，由已选特征提供类别的信息量不会发生变化。出现式（15）的情形：

表示候选特征的加入，产生冗余且无法提供新的信息，已选特征为类别提供的信息量减少。出现式（16）的情形：

表示候选特征带来新信息，已选特征为类别提供的信息量增加。

由式（14）～（16）可知，评价函数第一项的I(Fj；C|Fm)，度量候选特征的加入，已选特征和类别信息量的变化，其值越大，越有利于分类。评价函数第一项的I(Fm；C|Fj)，由第4章动态相关性特征选择算法可知，表示已选特征存在的前提下，候选特征与类别的信息量，度量候选特征对类别的贡献度。

但是，评价函数第一项的I(Fm；C|Fj)+I(Fj；C|Fm)是一个线性累加过程，当数值不断增大，会产生候选特征错选的问题［13-14］。DRFS 采用［0-1］标准化，缓解此问题，方法如下。

由互信息、交互信息、条件互信息定义［15］可得：

由式（17）、（18）及信息熵取值范围［16］，可得：

同理可得：

式（19）和（20）联立［9］，可得：

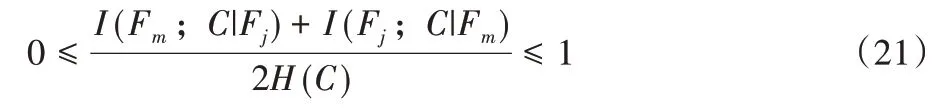
由式（17）～（21）可知，评价函数第一项的I(Fm；C|Fj)+I(Fj；C|Fm)完成［0-1］标准化，缓解线性累加所产生的候选特征错选问题。

评价函数第二项的I(Fj；Fm；C)，度量候选特征Fm和已选特征Fj的协同作用。由交互信息定义，可得：

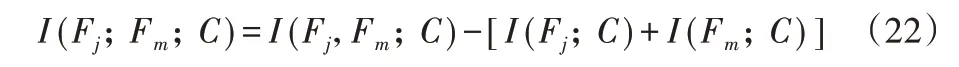
出现式（23）的情形：

表示已选特征和候选特征一起出现时，与类别产生的信息量，大于两者单独与类别产生的信息量之和，即发挥正向协同作用。出现式（24）的情形：

表示已选特征和候选特征相互独立，与类别的信息量不产生关联作用。出现式（25）的情形：

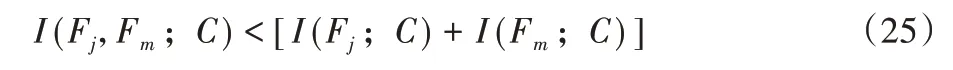
表示已选特征和候选特征存在冗余，发挥负向协同作用。

由式（22）～（25）可知，评价函数第二项的I(Fj；Fm；C)，度量候选特征和已选特征的交互相关性。

同样地，DRFS 采用［0-1］标准化，缓解评价函数第二项的I(Fj；Fm；C)线性累加，造成候选特征的错选问题，方法如下。

由互信息定义，可得：

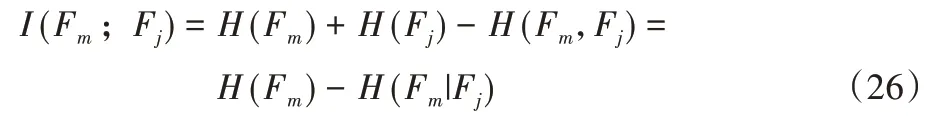
由互信息性质，可得：

由联合熵及联合互信息的性质［17］，可得：

由互信息性质，可得：

由式（22）、（28）～（30）联立［18］，可得：

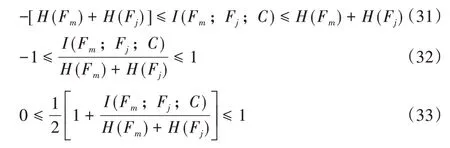
由式（26）～（33）可知，评价函数第二项的I(Fj；Fm；C)完成［0-1］标准化，缓解候选特征的错选问题［19］。

综上所述，DRFS 评价函数第一项的I(Fm；C|Fj)+I(Fj；C|Fm)，采用条件互信息，基于条件相关性，既度量了候选特征对类别的贡献度，又探究了已选特征和类别的动态信息量变化；DRFS 评价函数第二项的I(Fj；Fm；C)，采用交互信息，基于交互相关性，度量了候选特征和已选特征的协同作 用 ；DRFS 同时将I(Fm；C|Fj)+I(Fj；C|Fm) 和I(Fj；Fm；C)进行［0-1］标准化，尽可能防止在特征选择过程，因计算线性累加导致候选特征的错选问题。

DRFS 算法伪代码如算法1 所示。

算法1 DRFS算法。

DRFS 算法首先初始化变量（第1）～2）行）；然后计算每个特征与类别的互信息值（第3）～5）行）；筛选与标签具有最大互信息值的特征并添加到已选特征集合S中，完成第一个特征的选择（第6）～9）行）；最后，根据式（13）计算每个特征的条件相关性和交互相关性，确定最大信息量特征添加到已选特征集合S，并将其从原始集合F中删除，直到满足选择特征数K为止（第10）～18）行）。

5 实验

通过12 个数据集进行实验验证，以评估DRFS 算法的特征选择性能。仿真实验基于Windows 10 操作系统，处理器为Intel，3.30 GHz，内存为8 GB 的PC，通过Matlab 语言编程实现。

5.1 数据集

为验证所提算法的有效性，选取12 个数据集，其具体信息如表3 所示。

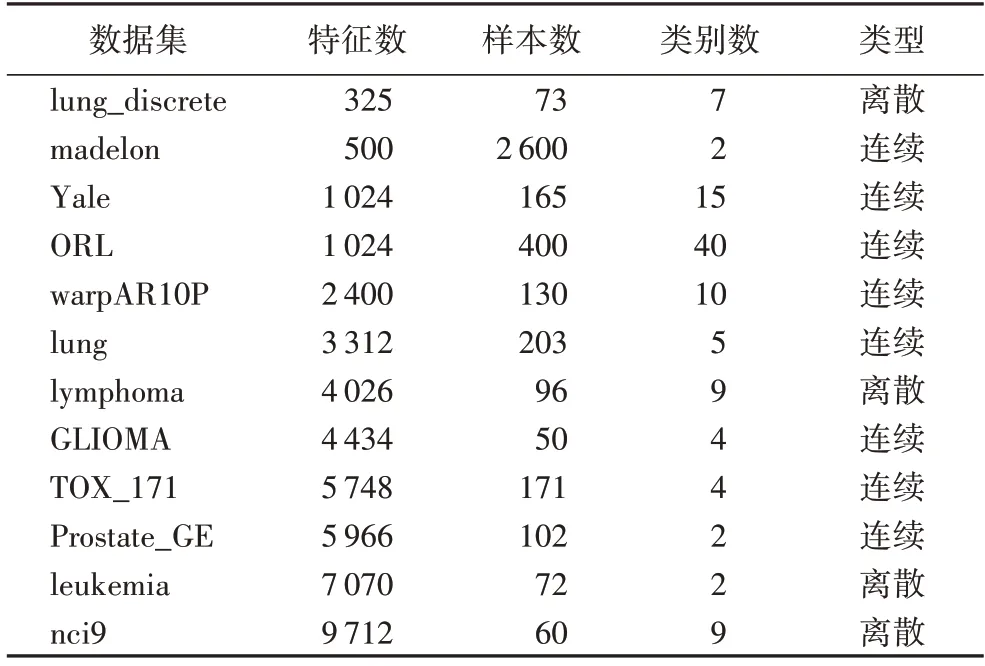
表3 实验数据集描述Tab.3 Description of experimental datasets

5.2 实验设置

仿真实验采用10 重交叉验证，每项实验运行10 次。本文算法与JMI［10］、mRMR［9］、最大相关和最大独立性（Max-Relevance and max-Independence，MRI）［20］、DCSF［2］、最小冗余性和最大依赖性（Min-Redundancy and Max-Dependency，MRMD）［21］算法通过分类准确率对比，选择特征数K=50。实验算法属于过滤式特征选择方法，故选择分类算法支持向量机（Support Vector Machine，SVM）和最近k邻居（k-Nearest Neighbor，kNN，k=3）进行分类。数据集的连续型数据采用分箱离散法处理，箱数设为5。

5.3 实验结果与分析

表4 和5 给出实验算法在仿真数据集的实验结果。

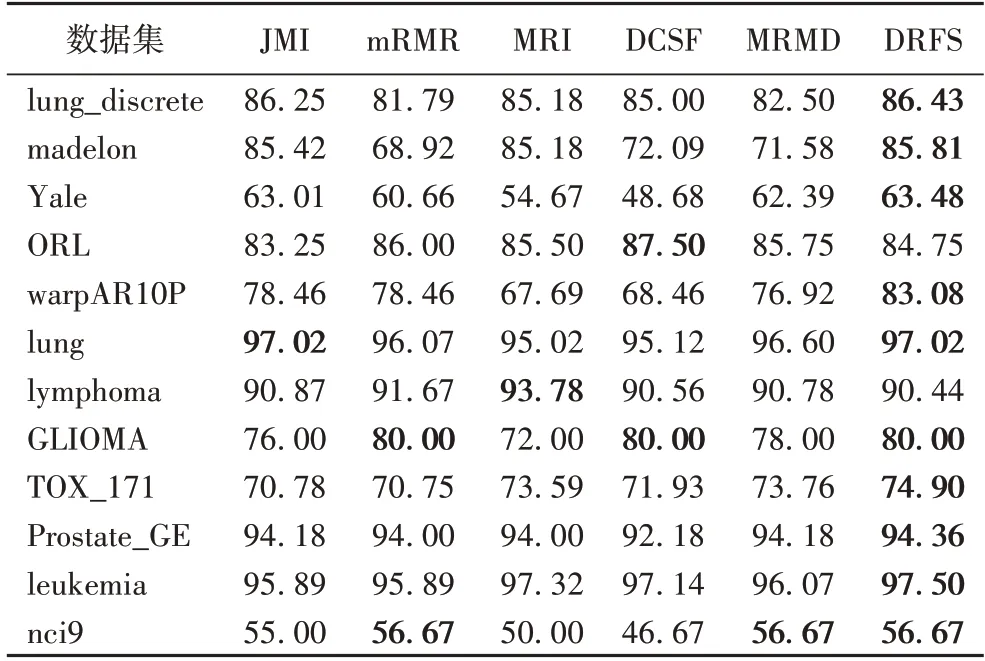
表4 不同算法在3NN分类器上的分类准确率对比 单位：%Tab.4 Comparison of classification accuracy of different algorithms on 3NN classifier unit：%

由表4 可见，DRFS 算法在10 个数据集上达到最优；由表5 可见，DRFS 算法在9 个数据集上达到最优。在3NN 分类器上，DRFS 算法与DCFS 算法相比，分类准确率最高提升14.8个百分点，数据集lung_discrete、madelon、Yale、warpAR10P、lung、TOX_171、Prostate_GE、leukemia、nci9 的分类准确率提升约6.89 个百分点，数据集ORL、lymphoma、GLIOMA 的分类准确率相近。在SVM 分类器上，DRFS 算法与DCFS 算法相比，分类准确率最高提升5.4 个百分点，数据集lung_discrete、Yale、ORL、warpAR10P、lung、lymphoma、leukemia、nci9 的分类准确率提升约1.75 个百分点，数据集madelon、GLIOMA、TOX_171、Prostate_GE 的分类准确率接近。

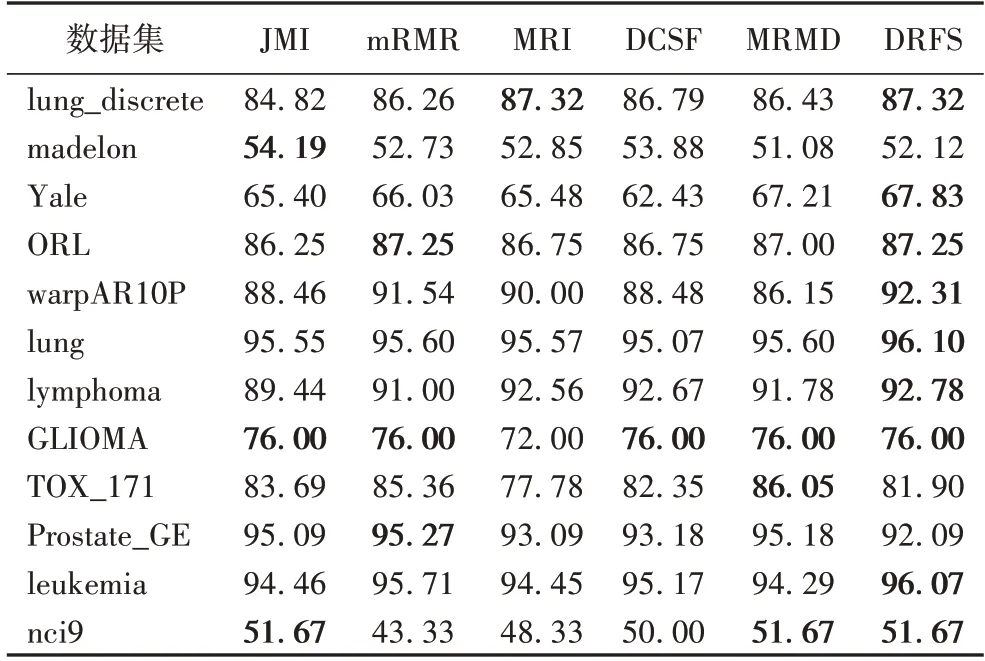
表5 不同算法在SVM分类器上的分类准确率对比 单位：%Tab.5 Comparison of classification accuracy of different algorithms on SVM classifier unit：%

由实验结果可知，mRMR 算法达到最优次数为5 次，仅次于DRFS 算法，根据式（10）分析，该算法采用了“最小冗余性-最大相关性”原则，并且使用已选特征集合基数的倒数缓解线性累加，但是没有度量交互相关性。JMI 算法达到最优次数为4 次，根据式（11）分析，该算法虽然度量交互相关性，但是计算平均条件相关，包含部分冗余信息，使得算法分类准确率下降。对于MRMD 算法，分析文献［21］，该算法提出了一个新的特征冗余项，它既包括了候选特征和已选特征之间的冗余，又考虑了候选特征和给定已选特征的类别之间的相关性。对于MRI 算法，分析文献［20］，该算法定义了一个新的互信息项，它既包含了候选特征提供的独立信息，又包含了已选特征保留的独立信息。MRMD 算法和MRI 算法，都从不同的角度评估已选特征和候选特征的关系，尽可能利用候选特征和已选特征提供的信息。

由实验结果可知，DRFS 算法总体优于DCSF 算法。由于DCSF 算法在特征选择过程中忽略交互信息带来的与分类有关的信息量，导致部分候选特征未选出，进而不能产生良好的特征子集。DRFS 算法从三个方面入手，1）采用条件互信息，在特征选择过程中动态地衡量已选特征与类别的条件相关性，同时度量候选特征提供的信息量；2）采用交互信息，度量候选特征和已选特征的交互相关性，即二者的协同作用。3）采用［0-1］标准化方法，一定程度上解决了线性累加导致的候选特征错选问题。由评价函数式（13）的理论分析及实验结果，表明DRFS 算法可以促进相关性计算更加准确，能够更好地选择特征子集。

6 结语

针对DCSF 算法在特征选择过程中忽略交互相关性的问题，提出基于动态相关性的特征选择算法DRFS。DRFS 算法使用条件互信息和交互信息，度量特征与类别的条件相关性和交互相关性，以提高特征选择分类准确率。实验结果表明，所提算法与DCSF 算法及其他特征选择算法相比，分类准确率有所提升。

DRFS 算法在度量条件相关性时仅考虑一个候选特征和一个已选特征，但特征选择过程中存在候选特征与多个已选特征具有条件相关性现象，故后续将会考虑使用多变量的条件互信息，度量候选特征与多个已选特征之间的条件相关性，进一步提升特征选择的分类准确率。