等截面双T平板挠度计算方法及试验研究

黄娟娟

(福建六建集团有限公司 福建福州 350014)

0 引言

预制预应力混凝土双T板(以下简称双T板)，是一种由宽大的水平面板和两个窄而高的肋梁组成的梁、板结合构件。其横截面呈现两个并排的T字，为单轴对称截面，具有刚度大、质量轻、抗裂性好的特点[1]。因其工业化生产和装配化施工的优势，目前已广泛应用于跨度较大，覆盖面比较广的厂房、礼堂和桥梁等工程领域，是目前国际上应用最为广泛的预应力混凝土板类预制构件。

目前，国内外预应力混凝土双T板的研究相对处于初步阶段，现行《预应力混凝土双T板(坡板宽度2.4 m、3.0 m；平板宽度2.0 m、2.4 m、3.0)》(18G432-1)[2]对预应力混凝土双T板挠度变形研究相对较少，在施工安装过程中，预应力混凝土双T平板的结构性能进行安装拼接之前，双T平板结构的挠度检验是工程施工中的必要环节。由于采用有限元分析计算较为复杂，工程人员应用难度大。因此，本文通过简化双T板截面惯性矩计算公式，将其代入挠度计算公式中，并将其计算结果与有限元分析结果和试验数值结果做对比，以验证该方法的适用性，期望能为现场挠度检验计算提供参考。

1 挠度计算

1.1 预应力构件挠度计算

在对预应力结构的进行力学分析时，通常将预应力作为加载外荷载前作用在混凝土构件受拉区的外力，对称的外力使得构件下部截面受压，上部截面受拉[3]。因此，在荷载作用下，可将预应力构件的挠度看作为由以下3部分组成[4]：

(1)先张法(后张法)张拉过程中产生的反拱挠度值f1；

(2)外荷载作用下产生的挠度值f2；

(3)外荷载作用下引起预应力筋拉力增量作用产生的反拱挠度值f3。

本文所研究的双T板为先张法预制构件，预应力筋产生的初始有效应力，可根据作用在体系上荷载变化时预应力筋应力的变化量得出。预应力构件通常是在锚固端和转向块处进行连接，设置在构件截面处的预应力筋相对构件是自由移动的，外荷载作用下引起预应力筋拉力增量基本可以忽略。因此，在外荷载作用下双T板的挠度，取决于外荷载与预应力筋的拉力作用。本文将预应力初始有效应力等效为外荷载作用，在预应力构件之前加在构件上的初始荷载，从而将预应力混凝土双T板挠度计算转化一般混凝土构件的挠度计算问题。

双T板为等截面结构，可通过采用积分法对双T板进行挠度计算，其挠度计算式[5]如式(1)所示：

(1)

式(1)中，θ为转角函数；f为挠度函数；E为弹性模量，由混凝土强度等级确定；M(x)为弯矩函数，并定义逆时针方向为“+”；I表示截面截面惯性矩，由计算获得；C、D为常数。

1.2 截面惯性矩计算

本文以规范中[2]的YTPb型双T平板作为研究对象，如图1所示，对于不同种类的YTPb型双T平板，h、R是一个变化值，截面参数较为复杂，不利于截面惯性矩计算，工程实际应用困难。为方便计算，本文通过对其截面进行适当简化，简化后的截面示意图如图2所示，其中，b的取值应根据转角半径R的大小适当调整。

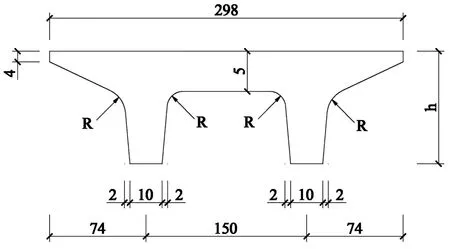
图1 截面参数示意图(单位：cm)

图2 截面计算参数示意图(单位：cm)

通过简化后的截面形式，计算该类型双T板的截面惯性矩I表达式。如图2所示的各截面A1、A2、A3及形心y1、y2、y3公式为：

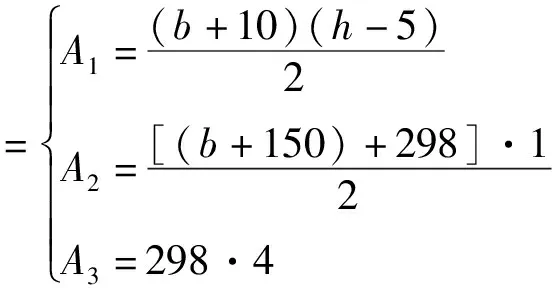
(2)

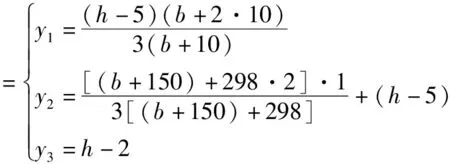
(3)

根据式(2)、式(3)求得双T平板形心z为：

(4)

获得各截面的截面惯性矩I1、I2、I3为：

(5)

综合式(2)～式(5)得截面惯性矩表达式为：

I=2I1+I2+I3

(6)

2 数值模拟计算

为验证式(6)的简化后的截面惯性矩公式是否能应用于实际挠度检验计算中，本文取YTPb2430-1型双T平板作为研究对象。通过采用Midas Civil有限元软件计算其实际截面在均布力加载和集中力加载作用下的跨中挠度值，代入式(6)的挠度计算公式计算出的结果做对比。

取YTPb2430-1型双T板的弹性模量E=3.35×107kN/m2，挠度检验荷载为标准组合值Qk=3.00 kN/m2(扣除双T板自重)，拟定均布力加载值q=15.4 kN/m，且长度为0.76 m，集中力加载值为F=11.7 kN，加载方式如图3所示。将预应力初始有效应力等效为外荷载作用在预应力构件之前，加在构件上的初始荷载，序号①～⑦表示加载等级，由①级向⑦级逐级加载，且x1=1.00 m、x2=1.25 m、x3=1.50 m、x4=2.94 m，l=21.88 m。

图3 加载简图

根据YTPb2430-1型双T平板的截面数据及图1截面参数，取h=1.00 m，R=0.075 m，适当调整b的值为0.148 m，其他尺寸参数如图2所示。计算得出该类型双T平板的截面惯性矩I=0.03716 m4，与实际截面惯性矩I=0.03727 m4相比，仅偏差为0.30%，拟合较好。

2.1 均布力加载挠度计算

结合跨中挠度计算公式，均布力加载下的跨中挠度计算程序如下：

跨中挠度计算与有限元计算结果如表1所示。

由表1可以看出，均布力加载下，跨中挠度计算程序的结果与数值模拟结果较为接近，偏差率在0.46%～1.54%之间，拟合效果较好。

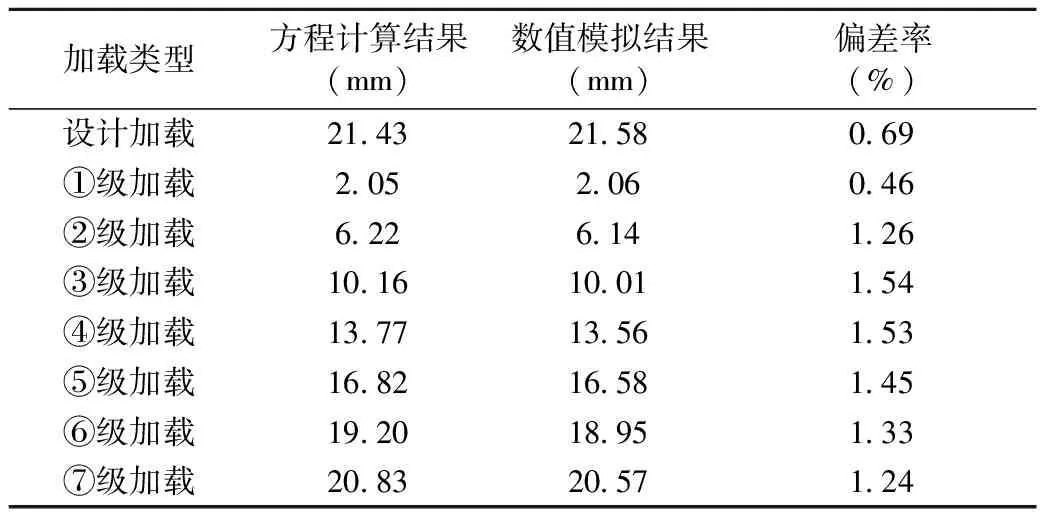
表1 均布力加载计算结果

2.2 集中力加载挠度计算

结合跨中挠度计算公式，集中力加载下的跨中挠度计算程序如下：

跨中挠度计算与有限元计算结果如表2所示。

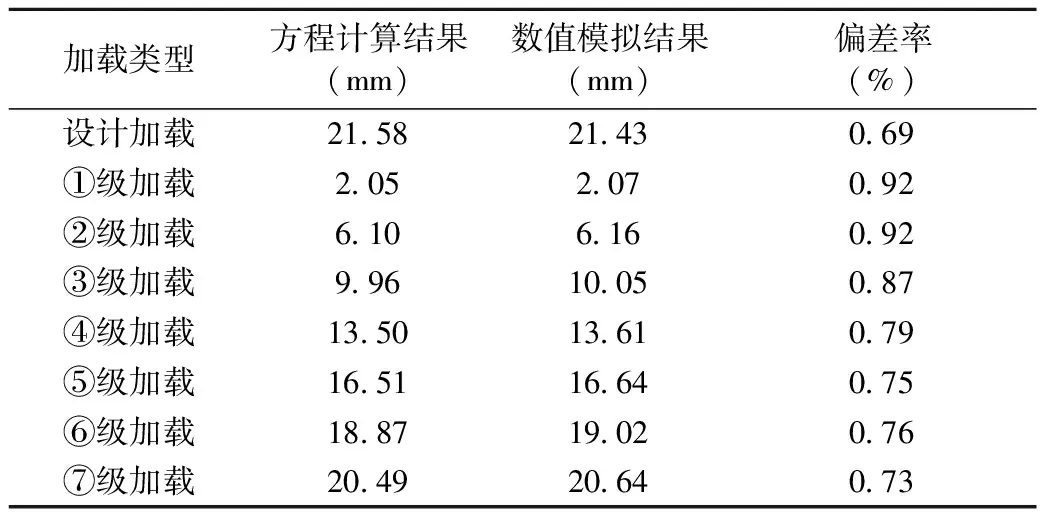
表2 集中力加载计算结果

由表2可以看出，集中力加载下，跨中挠度计算程序的结果与数值模拟结果较为接近，偏差率在0.69%～0.92%之间，拟合较好。

综上，式(6)截面惯性矩公式拟合较好，能够应用到挠度检验计算中。

3 试验案例

3.1 工程概况

为进一步验证简化后的式(6)能够应用于实际工程挠度计算中，本文拟通过某公司生产的YTPb2430-1型(21.88 m)预应力混凝土双T板荷载试验结果与理论计算结果进行对比。图4为YTPb2430-1型(21.88 m)预应力混凝土双T板，其构件实际跨度为21.88 m。正常使用极限状态荷载标准组合值Qk=3.00 kN/m2(扣除双T板自重)[6]。

图4 YTPb2430-1型双T平板

荷载试验采用混凝土预制块进行加载，混凝土预制块为梯形体，每个重量约为1.194t。混凝土预制块加载平面布置示意图如图5所示，满载情况下试验荷载效率如表3所示。

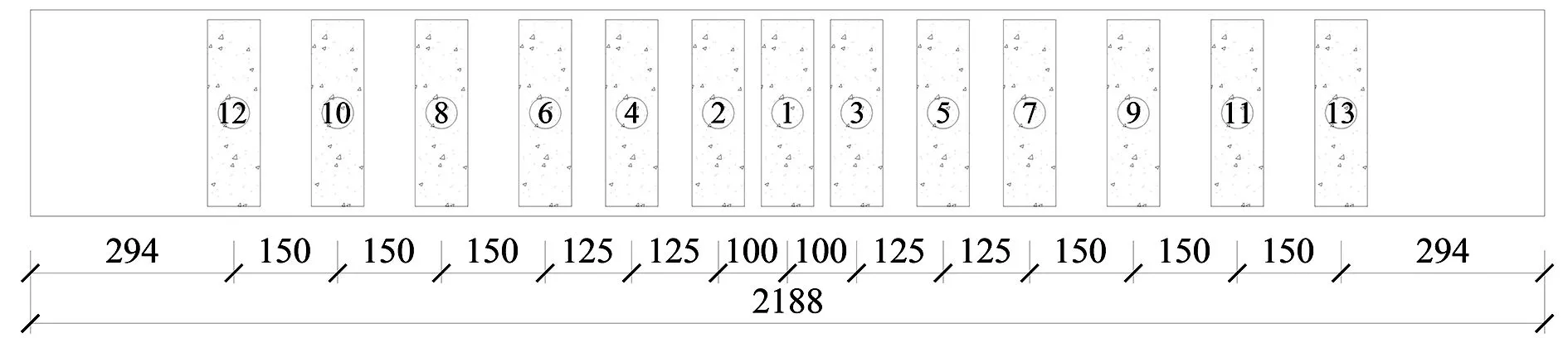
图5 预制块加载平面布置示意图(单位:cm)

表3 设计加载计算结果

双T板加载分级情况如图3所示。静载正式试验前对双T板进行预压，预压卸载完成后进行正式加载，正式加载分为七级，每级加载完成后，持续10 min～15 min；满载作用下持续30 min。在持续时间结束，并达到变形稳定时，测读各级荷载作用下端部及跨中的百分表读数。

3.2 试验结果

本文试验的挠度理论计算采用均布力加载方式计算，计算结果即为本试验的理论计算结果。试验后获得一级加载至七级加载的跨中挠度值，如表4所示。

由表4可以看出，本文采用的挠度计算方法能够很好地反映出试验实际的跨中挠度，计算结果与挠度试验检验结果较为接近，其偏差率在0.28%～2.56%之间，该结果能简化有限元的计算过程，可为试验方案的拟定以提供简单的计算方式，为现场挠度检验提供参考依据。

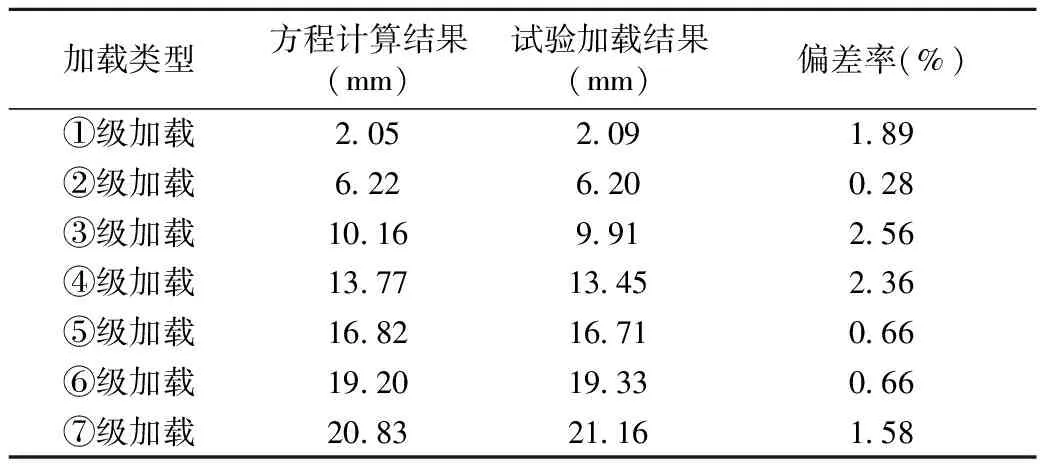
表4 试验加载结果比较

4 结论

本文通过简化规范[2]中YTPb型等截面双T平板的截面惯性矩计算方法，将其应用于挠度计算公式中，并将其计算结果与有限元分析结果和试验结果做对比，得出结论如下：

(1)根据本文所研究的等截面双T平板的截面参数，提出了简化后的双T平板截面惯性矩计算方法，计算结果与实际截面惯性矩仅相差在0.3%以内，吻合较好。

(2)通过有限元计算方法验证，均布荷载作用下和集中力作用下的有限元分析结果与公式计算结果误差分别在0.46%～1.54%与0.69%～0.92%之间，误差在允许范围之内，吻合较好。

(3)结合现场试验数据对比，发现公式计算结果与试验挠度检验结果误差在0.28%～2.56%之间，误差在允许范围之内，吻合较好。

综上，本文简化了规范[2]中的YTPb型等截面双T平板的截面惯性矩计算方法，可应用于其挠度计算中，可为现场挠度检验计算提供参考。