反向教学设计方法在《大地测量学基础》课程中的应用

林 鹏 裴媛媛 高旭光

(安徽建筑大学土木工程学院 安徽合肥 230601)

0 引言

随着“以本为本，四个回归”的高等教育理念的提出，如何激发学生兴趣、增强学生的主观能动性，进而提高教学质量、全面提高学生的综合素质，是当下本科教育面临的一大挑战[1-2]。

教学设计是依据学习目标，对评估反馈与教学活动进行设计。因此，设定合理的学习目标是进行教学设计的核心[3]。传统的教学设计，是先确定教学活动与评价方式，然后引导学生学习相应的教学内容，实现相应的教学目的。但该设计方式是以教学内容为核心进行教学设计，若不能将学习目标、评估反馈以及教学活动之间相互匹配，某一环节的缺失则会产生不佳的教学效果。因此，基于目标导向的教学设计是匹配学习目标、评估反馈与教学活动的有效方法。王丽等以《化工设计》课程为例，将基于目标导向的教学设计融入线上课堂，构建了过程形成性评价框架及思路[4]。杨亚林等构建了基于目标导向的翻转课堂，解决了学生难以理解在三维空间推演和表达的问题,促进了学生的空间思维与想象力，提高了教学效果[5]。赵炬明对目标导向的教学设计进行了改进，提出了反向教学设计的方法，并将教学目标区分为一般目标和具体目标，并以此确定相应的教法与学法，保证了学习目标、教法、学法以及评价一致[6]。

《大地测量学基础》作为测绘工程专业的核心必修课，在专业培养中占据核心地位[7]。然而，该课程理论知识抽象且复杂，导致学生学习效果不佳。鉴于此，常亮等采用分组教学的方式，提高学生对重点知识的掌握与理解程度[8]。刘志平等将《大地测量学基础》与其他专业课相结合的方法，以解决该课程内容多而课时少的矛盾[9]。丁士俊等采用启发式教学的方式，克服传统“填鸭式”教学的弊端，改善了教学效果[10]。因此，对授课内容进行科学合理的设计是引导学生学习、激发学习兴趣以及达到相应的教学目标的基础。

鉴于上述分析，本文以《大地测量学基础》中的坐标转换为案例，结合CDIO理念进行基于目标导向的教学设计，旨在激发学生的学习兴趣，使学生更易掌握讲授的知识点，提高课堂教学质量。

1 反向教学设计案例

1.1 设计思路

坐标转换是《大地测量学基础》中的重点教学内容之一，其本质上是对点位空间位置变化的描述，需要学生具备一定的空间想象力理解坐标转换的过程，对学生抽象思维的要求较高。为了增强学生对该内容的理解与掌握，以学习目标为导向，建立“目标-评价-教法”一体的反向教学设计方法，首先根据所需的教学结果来确定学习目标，根据可接受的反馈证据决定评价方法，最后选择合适的教学活动来进行课堂教学。因此，“目标-评价-教法”一体的反向教学设计可以确保教学目标、评价与课堂教法相互匹配，具体设计过程如下：

(1)基于布鲁姆认知学的学习目标的确定

根据布鲁姆认知模型，将认知目标分为六个层次，分别为记忆、理解、应用、分析、评价以及创造，并结合可量测的动词来进一步细化学习目标，具体如表1所示。依照布鲁姆认知模型，在坐标转换内容中，确定的教学目标如表2所示。

表1 布鲁姆认知模型及对应的可量测动词

表2 一般目标与具体目标

(2)评价方式的设计

根据教学目标，基于目标匹配原则确定教学评估方式，具体如表3所示，并且结合Rubric评分量表制作对应评分标准，以保证学生的学习效果得以正确反馈，其中表4展示了目标C的Rubric评分量表。

表3 基于目标匹配原则的教学评估设计

表4 目标C的Rubric评价量表

(3)教学活动的设计

首先，根据目标A设计课堂互动环节，基于雨课堂教学平台中的课堂弹幕功能设计目标A的互动环节，通过浏览学生发送关于“简述一个需要坐标转换的场景”问题的弹幕，及时掌握学生对于该内容的认知程度。然后，根据课件(图1)分别采用GPS与BDS测量了若干个点位坐标，且二者的坐标基准分别为WGS-84与CGCS2000坐标系，进而引出问题“如何将WGS-84坐标转换至CGCS2000”，并对教学内容进行详细解释说明，使学生能正确掌握坐标转换的概念。

图1 坐标转换问题背景设定

其次，针对目标B，结合PPT动画展示平面四参数与三维七参数转换模型，并设计启发性问题，如图2所示，引导学生结合间接平差的基础知识来解决坐标转换的过程。随后进行课堂讨论，例如：求解该参数至少需要几组观测值、该函数模型如何线性化等，引导学生如何独立自主学习该部分的知识，最后完成过后设置一个简单的实际案例进行课堂互动，要求学生“简述一下坐标转换的基本过程以及如何求解转换参数”，以及时评估学生对知识点的掌握程度。随后给出转换参数的求解过程并对过程进行详细讲解，如图3所示。最后，以自己参与研发的坐标转换软件为例来与计算进行对比验证，展示目前与专业相关的软件的基本操作过程，如图4所示。

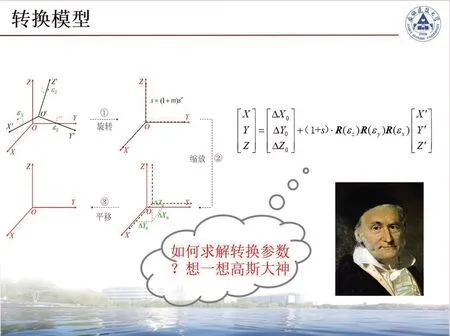
图2 转换参数求解的启发性问题

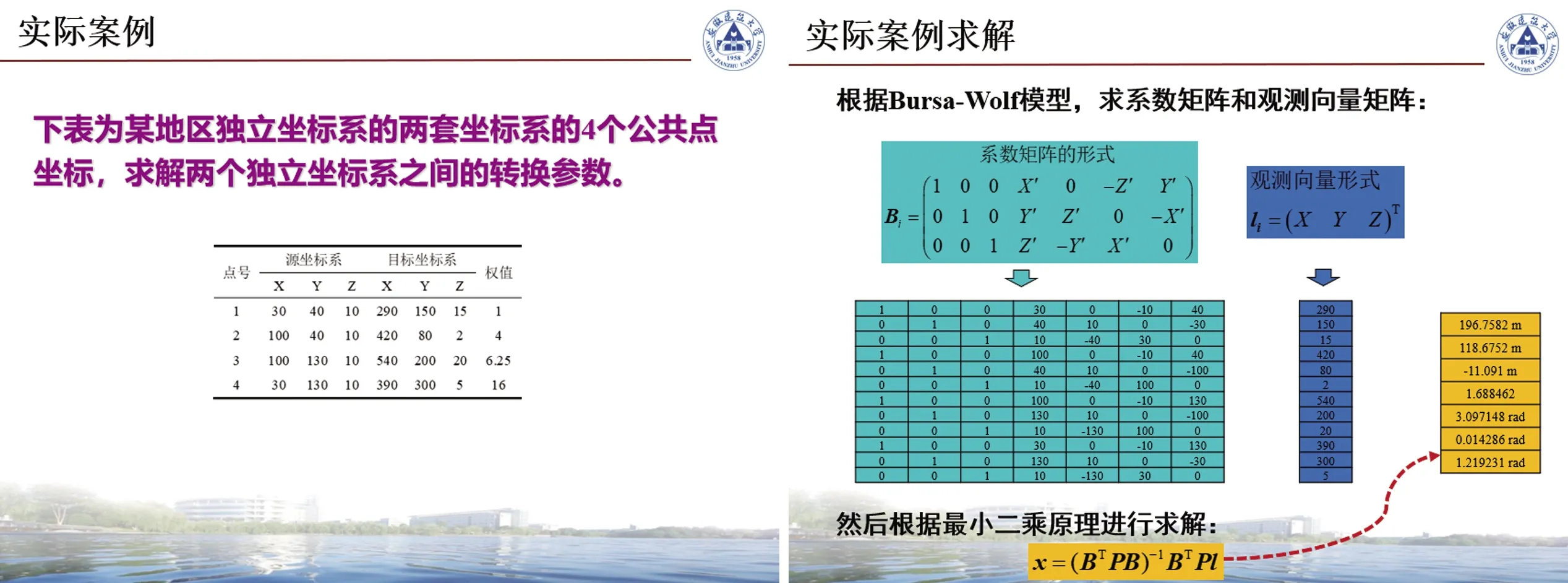
图3 实际案例及结果

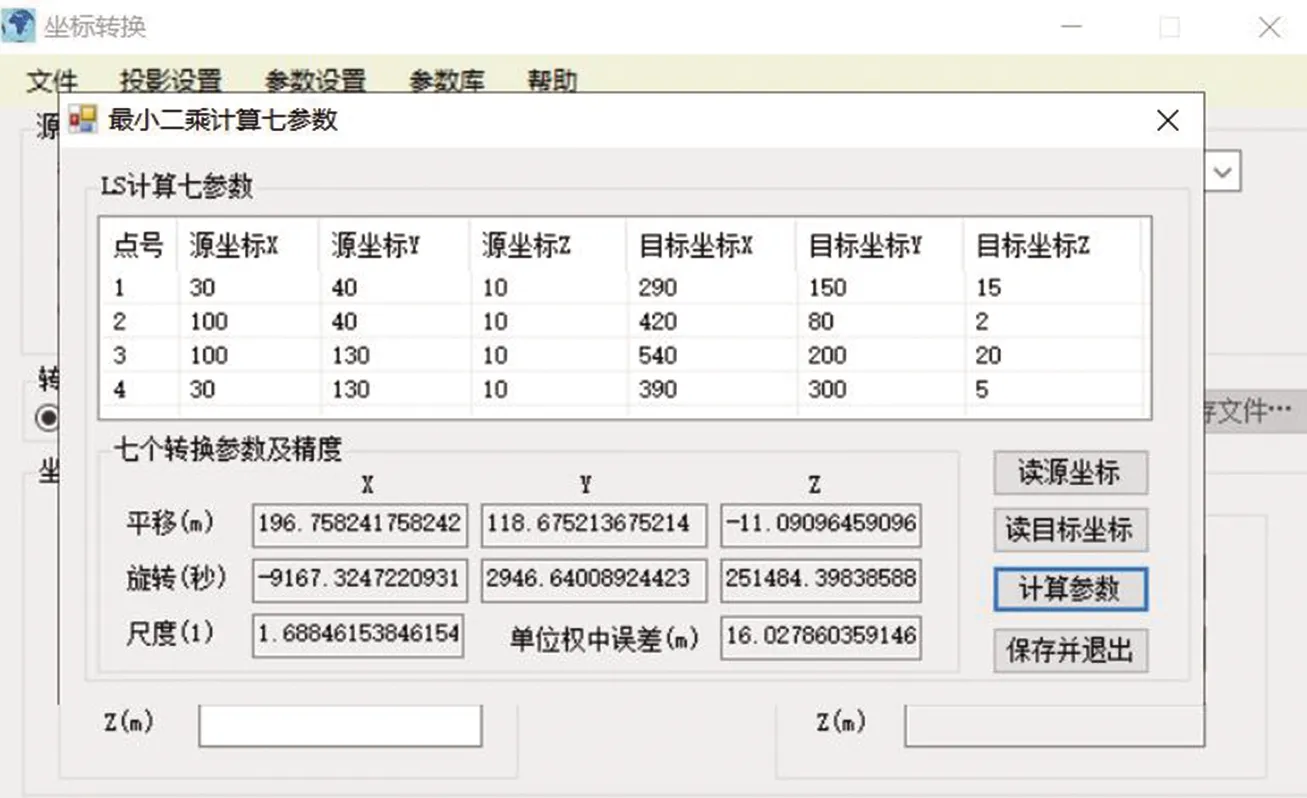
图4 专业软件求解结果

第三，如图5所示，设置一个坐标转换案例计算作为课后练习。在设计课后练习时，考虑到如何能科学评价学生独立自主完成课后训练，将课后练习设计为同题不同数据。基于MATLAB平台，以相同的中误差生成不同的随机误差并加入坐标真值数据中，并将学生学号后两位作为先验单位权中误差，保证学生面对相同题目的同时保证数据不一致，将学生实际学习情况进行反馈，以达到公平客观评价的目的。通过设计Rubric评价表格(表5)，这样根据每位同学的计算结果，可以对每位同学的平时成绩进行客观科学的评价。

图5 坐标转换课后练习

表5 课后练习题的Rubric评价量表

3 结论

本文探讨了反向教学设计法在《大地测量学基础》课程中的应用，并以坐标转换为案例，将该理论应用于实际教学中，对基于目标导向的反向教学设计进行了重点阐述。在实际教学过程中，通过此种方法设计的教学活动，可以有效地调动学生的积极性，提高学生自主学习的主观能动性，课堂教学气氛有效提高了教学质量。