极限思维法在初中物理解题中的运用

施燕莹

(江苏省南通市崇川初级中学 226001)

相比于其他学科，物理具有一定的严谨性和逻辑性，如果学生没有掌握正确的解题方式，尽管已经掌握教师课堂所讲的物理知识，但是在解决问题的实际过程中，仍然会感到无措，不知如何下手.因此，教师需要有意识地引导学生利用极限思维法解决初中物理实际问题，锻炼学生的解题能力，提高学生的物理意识.

在学习物理过程中，学生可能会遇到各种各样奇形怪状的问题.解决的方式可以简单也可以复杂，关键是学生能否在最短的时间内找到最方便以及最简单的解题方法.极限思维就是直观的解题法，对学生解题能力的提升具有一定的促进作用.近年来，这种解题方法在初中物理解题过程中，得到了较为广泛的使用.如果学生运用这种思维，可以进行灵活的解题，那么可以在一定程度上减轻其解题的压力.这种解题方式不仅是让学生在解题过程中，可以快速的找到解题的思路以及方法.还有利于把复杂的问题变得简单，那学生在解题过程中，可以达到事半功倍的效果.因此，文章对极限思维的运用进行了深入分析，其目的在于如何真正提升学生的解题能力以及效率.

1 什么是极限思维？

直线思维是从极端的角度作为出发点，就好像是一种比较夸张的假设法.但是通过假设后，物理原理就变得更容易的理解和接受了.这样分析，简单来说，极限思维就好像是物理的一条方便路径.我们先对问题进行假设，然后通过假设反带入结果，以此作为推导，让假设可以成立.这种方法看似走了捷径，实际上是一个思维缜密的解决方法.相比拿到题目就开始投入大量的计算，会更加的方便和高效.在初中物理的教学过程中，通过引导学生发展极限思维法.可以拓展他们的物理思维边界，打开一种新的思考方式.为之后学习物理打下扎实的基础.

在物理学常用的方法中，极限思维是最受到人们所喜爱的，而且也方便每一个人掌握.可以科学直观的解决物理上一些比较难解答的实验结论.有总体上分析，就是将一个难以立刻解决的物理过程，一步一步的拆解分析，并把这个过程的双方极限值带入公式运算中.这时我们就会发现，物理过程的变化值都在两个极限之内，与我们所提出的假设是相符合的.这种思维方法对于初中物理教学发挥了非常大的作用.

2 极限思维法的正确运用方式

第一，找到突破点.初中阶段刚接触物理知识时，很多学生会觉得物理机深奥又很神奇，很难透彻的理解物理的规律以及原理.而且我们所拿到的题目信息，又带有很多迷惑性.让一些学生在思考之后，仍然得不到结果.这种时候，我们就可以运用极限思维法，观察题目中可用的信息量，采用假设法重新的解决此问题.寻找并分析已知条件，思考这些条件，选择合适的量值进行假设，从而找到新的解题思路.

第二，有效提升解题的效率.其实为在一定程度提高了解题的速度，简化了需要大量计算的问题.例如在研究凸透镜的物距以及像距规律时，可采用一些极端数据进行计算和分析.比如当物距无限大，或者物体到凸透镜的距离等于凸透镜焦点一倍或两倍距离时，得出的数据都非常有趣.有了清晰的思路，就可以加快解题的效率.

第三，对所得的答案进行验证.熟练运用好这个解题思路之后，需要注意验证答案的结果.找到变量中一个最容易的量代入计算，看计算结果是否符合假设的内容.

3 如何使用极限思维法

3.1 通过极限思维法寻找解题关键

学生在求解物理问题时，受到思维发展的限制，无法从物理题目中获取有效的信息，不知如何下手，解题效率不理想.当出现这种情况时，教师需要合理引导学生，指导学生利用极限思维法解决初中物理问题，既帮助学生掌握课堂所学知识，同时有利于锻炼学生的解题能力，发展学生的思维.

例1在一个盛满水的容器中竖直放置一块木板，如图1所示，静置一段时间后，部分木板浮于水面上，如果裁去如图1所示虚线以下的木板部分，则剩余的木板会如何变化？

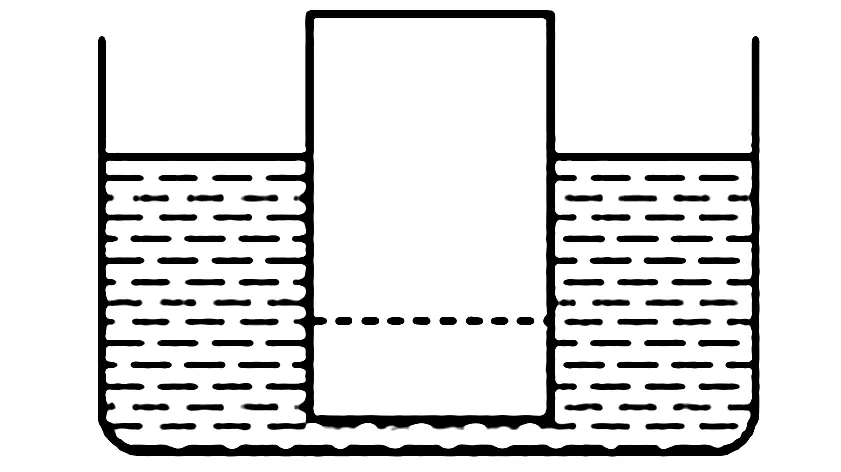
图1

解析这种题目乍一看很难，但是学生只需要仔细读题，抓住题目中的解题关键，即可求得答案.但是学生容易受到传统教学的影响，通过测量物体的密度进行求解.根据f浮=G物，列出式子ρ物gV物=ρ水gV排，又因为静止状态时，物体呈漂浮状态，如果裁去部分木板，物体的体积变小，如果物体继续保持漂浮状态，则V排也应当减小，所以木板的位置会有所下降.这种解题方式虽然能够解决物理问题，但是耗时较长.教师需要指导学生利用极限思维进行求解.假设将水面下的全部木板裁去，如果木板想要继续保持漂浮状态，则需要下沉一部分.利用极限思维法能够快速求出答案，学生的解题效率得以提高，有利于初中物理解题课堂教学工作的顺利进行.

3.2 通过极限思维法锻炼解题能力

一般情况下，学生在求解初中物理问题时会将课堂所学的知识代入到其中，利用公式进行分析和求解.虽然能够解得答案，但是通过这种方式，需要多个步骤，学生容易发生遗漏步骤的现象，导致最终答案错误.因此，教师需要引导学生利用极限思维法分析初中物理题目，确保学生的解题效率和准确率.

例2如图2所示，在天花板上固定一个滑轮，用一根绳子通过定滑轮将一个重量为G的物体拉起，如果将绳子AC换为长度更长的绳子AC′，当整个装置静止时，直杆AB的压力N和绳子所受的拉力T如何变化？

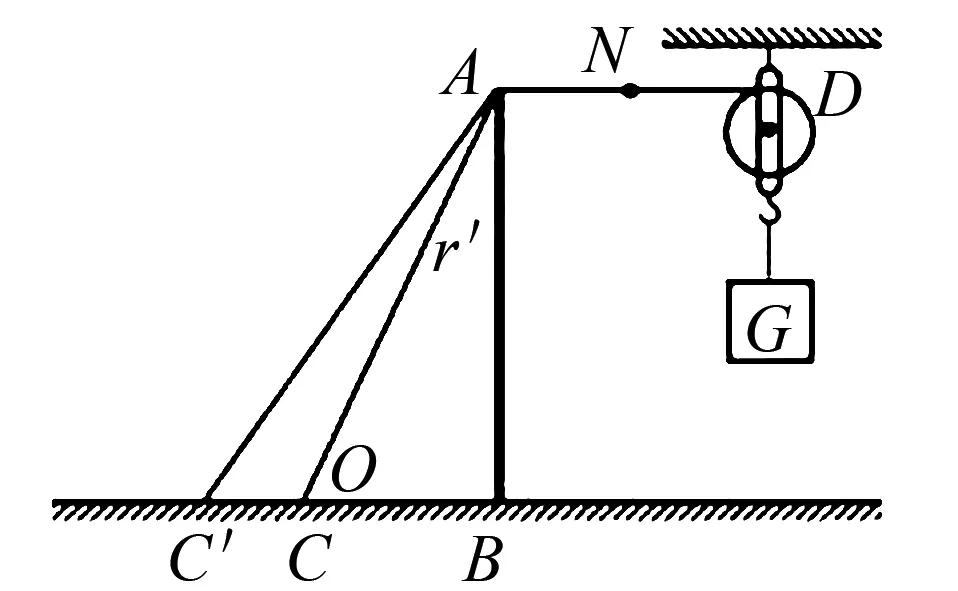
图2

解析力的问题是学生在初中学习物理阶段经常遇到的问题之一，因为物理条件的多变形，学生难以准确掌握解题方式.教师应当有意识地指导学生，锻炼学生的解题能力.一般情况下，学生会通过牛顿第三定律列出式子N′-Tsinθ=0，G-T′cosθ=0进行求解.这种解题效率并不是很理想，教师应当适当引入极限思维法.根据牛顿第三定律N′=-N′，T′=-T，将所有式子联立在一起，可以得到相关的联系，即T=gcosθ，N=gtgθ，当θ角度越小，T会随之减小，N也会随之变小.由此也可以看出，利用极限思维法求解初中物理题型，效率高和准确率都有所保证.

3.3 通过极限思维法发展物理思维

学习物理知识是初中阶段的学生必须完成的任务，作为知识的传授者，教师需要严肃认真对待.教师应当从学生的兴趣出发，充分调动学生的热情，鼓励学生参与到教学活动中，使学生感受到物理的魅力.而提高学生的解题准确率，增强学生的自信心是必须的，教师需要不断强化学生的思维训练，进而提高学生的学习效率.

例3固定一个斜面如图3，将一个物体放置在该斜面上，给物体一个平行于斜面的力F，试分析斜面的机械效率？

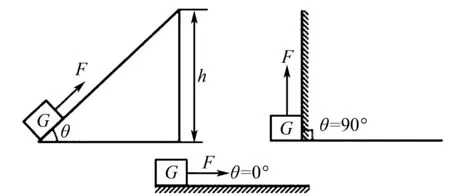
图3

解析力是学生在初中阶段最长遇到的物理题型之一，教师需要科学教导学生，帮助学生掌握相应的解题技能，促使学生全面发展.物体向上拉，会产生一个摩擦力f，物体克服重力G和摩擦力f做功，学生可以根据此列出式子F-Gsinθ-f=0，f=F-Gsinθ，摩擦力做功越多，斜面机械效率越小，又N=Gcosθ，所以f=μN=μGcosθ, 所以可以得到推论当θ角度变小时，压力N变小，摩擦力f也变小，则额外功变小，斜面机械效率变大.为保证解题的准确性，教师可以引导学生验证.当斜面垂直于地面时，N=Gcosθ=Gcos90°=0，f=μN=μGcosθ=μGcos90°=0，此时不做额外功，斜面机械效率最大.当斜面平行于地面时，N=Gcosθ=Gcos0°=G，f=μN=μGcosθ=μGcos0°=μG，此时额外功最大，斜面机械效率最小.通过极限思维法进行求解，既锻炼学生的解题能力，又发展学生的解题思维，有利于促使学生全面综合发展.

在上述的例题中，我们可以看到，利用极限时，为是一种极为灵活的思维方式.可有效解决多种物理的问题，且具有极高的解题速度.初中物理中有很多地方可以使用极限思维，在教学过程中结合有关的问题，将传统方法以及现实为进行对比.运用传统方法训练学生推理.利用极限思维培养学生的思维跳跃性.使用这两种思维进行解题，对于学生都有一定的帮助.而作为学生来说，要对每一种题型进行多角度的分析，判断变量是否出现连续变化，利用多种题型训练常见的思维解决方法.必要的时候请教教师，在形成一定的思维之后，可以快速的找到最合适解题的方式，有效提高解题速度.

综上所述，极限思维法在初中物理解题中运用广泛，教师需要合理地引导学生通过极限思维法进行分析和求解，锻炼学生的物理解题能力，提高学生的解题效率，确保答案的准确性，进而保证初中物理解题课堂教学的顺利开展.