基于互质阵列孔洞分析的稀疏阵列设计方法

刘 可 朱泽政 于 军 马俊达

①(哈尔滨理工大学测控技术与仪器黑龙江省高校重点实验室 哈尔滨 150080)

②(哈尔滨理工大学自动化学院 哈尔滨 150080)

1 引言

均匀线阵是最常用的阵列配置方式，由于其简单的阵元排布结构和完备的参数估计方法，使其广泛应用在目标方位估计、频率估计、目标跟踪等阵列信号处理相关的各个领域[1，2]。由阵列天线基本原理可以得出：对于配置N个传感器的均匀线阵，多重信号分类[3，4]( MUltiple SIgnal Classification，MUSIC)、旋转不变子空间[5，6]( Estimation of Signal Parameters via Rotational Invariant Technique，ESPRIT)等传统算法只能估计N-1个信源角度。而且由于均匀线阵相邻两个传感器的间距较近，容易产生耦合效应，严重影响DOA(Direction Of Arrival)估计性能[7，8]。

针对上述问题，稀疏阵列设计是提升目标分辨能力、减少相邻阵元耦合的有效方法。近些年来，最典型的稀疏阵列设计包括最小冗余阵列[9]、嵌套阵列[10，11]和互质阵列[12—14]。最小冗余阵列[9](Minimum Redundancy Array， MRA) 增大了相邻阵元间距，在减少阵元耦合效应的同时，可形成大量的虚拟传感器。虽然MRA可提高DOA估计性能，但是并没有给出阵列设计相关的物理表达式，使其应用范围受到较大限制。而嵌套阵列[10](Nested Array， NA) 的出现为稀疏阵列设计迎来了突破，它不仅具有与阵元间距和传感器个数相关的数学表达式，而且其子阵产生的差分共阵无延迟孔洞，使得子空间方法得以有效应用，其不足之处在于子阵阵元间距稠密，易发生阵元互耦，导致角度分辨性降低。互质阵列[12](CoPrime Array， CPA)的出现一定程度缓解了该问题，它同样由两个子均匀线阵构成，阵元间距是一对互质整数，由于其虚拟传感器存在大量孔洞，因此差分共阵不能高效利用。

在上述稀疏阵列基础上，最近几年出现了多种稀疏阵列改进方法。文献[13]提出了多级互质阵列，它由多个均匀线阵构成，其中每个子阵中的阵元数目和阵元间距为成对的互质整数。相比于互质阵列，其阵列孔洞进一步减少，连续延迟有所增加。文献[14]提出了两种线阵结构，分别是压缩间距方法 (Coprime Array with Compressed Interelement Spacing， CACIS) 和移动子阵方法(Coprime Array with Displaced Subarrays，CADiS)。CACIS对互质阵列其中一个子阵的阵元间距进行压缩处理，而CADiS是移动互质阵列的一个子阵到特定位置，两种方法都能提高阵列的连续虚拟延迟，增加阵列自由度，但是上述两种方法的虚拟阵元仍存在大量孔洞。针对连续延迟的利用问题，已有文献[15—18]给出了多种解决方案，但是由于网格失配和计算时间问题，现有方法在估计精确性和算法实时性方面仍存在较大的改进空间。因此，综合上述情况，如何提高连续虚拟传感器器数量，以便于利用MUSIC方法进行有效估计，仍然是获得目标DOA最直接、高效的方法。

受移动物理阵元以填充阵列孔洞思路启发，本文通过对差分共阵的影响阵元进行有效分析，提出了两种基于互质阵列结构的改进方法，增加连续延迟数量、提高DOA估计性能，其主要贡献可概括为如下3个方面：

(1)分析互质阵列的差分共阵所产生的虚拟延迟与特定物理阵元关系，得出互质阵列在去掉冗余阵元后，将不改变连续虚拟阵元；

(2)对阵列结构进行有效优化，移动互质阵列的冗余阵元到特定位置，实现物理阵元数不变，孔洞有效减少，DOA估计能力有效提升；

(3)推得了提出的两种阵列设计方法连续延迟和自由度相关数学表达式。

2 互质阵列模型及互耦模型

2.1 互质阵列模型

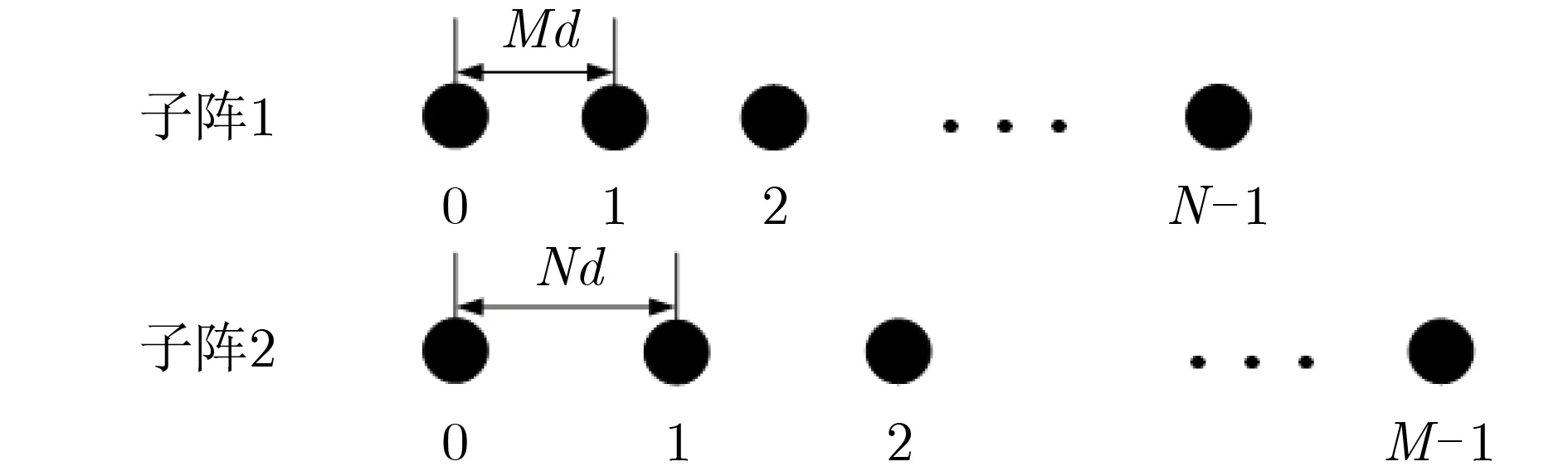
图1 互质阵列结构图

2.2 互耦分析模型

由于阵列相邻阵元间距过近，容易产生耦合效应，考虑式(1)中阵列模型存在阵元互耦，则接收向量可以表示为

3 提出的稀疏阵列设计

3.1 互质阵列延迟分析

要想满足该不等式，只能N=2，M=3，或者N ＞2，M= 2，其与条件矛盾，所以该假设不成立，因而可得N(M-1)＞M+N-1。所以这两个元素都大于M+N-1，并不影响阵列的连续延迟。证毕

由性质1可知，在M和N满足一定条件下，去掉位置0的元素，阵列中对称一侧的正延迟只减少2个，且绝对值不相等，则整个差分共阵延迟只减少4个，但是连续延迟并没有改变，不影响连续延迟拓扑。因此，利用MUSIC算法估计信源DOA，将不影响算法性能，同时可以减少设备成本和虚拟阵元冗余。上述分析启发本文研究新型的稀疏阵列配置，通过优化阵列结构，改善差分共阵的延迟拓扑，提高DOA估计精度。下面引出提出的两种阵列配置方法。

3.2 提出的阵列设计1

提出的阵列设计1如图2所示，该设计方法将0位置元素移动到位置-M，形成了新的阵列设计方法。定义 S为提出阵列中所有阵元的位置，则S可以表示为

图2 提出阵列设计1结构图

要想满足该不等式，要求N=3，M=5，4，2或者N=4，5，M=3，2，或者N ≥6，M=2，上述情况均与条件矛盾，所以N(M-1)＞2M+N-1，即连续的虚拟延迟范围为[-2M-N+1，2M+N-1]证毕

3.3 提出的阵列设计2

提出的阵列设计2的阵列结构如图3所示，该方法将0位置元素移动到位置-N，以此优化阵列结构。定义S 为提出阵列的阵元位置，其可以表示为

图3 提出阵列设计2结构图

4 仿真实验

本节选取互质阵列(CPA)、提出的阵列设1(Proposed Method1， PM1)、提出的阵列设计2(Proposed Method2， PM2)和文献[13]提出的方法开展DOA估计性能比较，以验证提出方法的优越性。为了公平比较，选用相同物理传感器数目、相同的DOA估计算法(MUSIC)为前提条件，并给出了克拉美罗界[19](Cramér—Rao Bound， CRB)曲线作为参照，提出的阵列设计1和提出的阵列设计2的阵列参数为M=4和N=7，文献[13]选择三级互质阵列，阵列参数m1=2，3，7。因此，上述每个阵列共有10个阵元。

4种阵列产生的虚拟传感器位置如图4所示。互质阵列产生的连续延迟范围是[-10，10]。提出阵列设计1和提出阵列设计2产生的连续延迟分别为[-14，14]和[-17，17]，文献[13]阵列产生的连续延迟为[-16，16]，提出的阵列设计方法连续阵元数明显多于互质阵列。另外，从差分共阵所形成的总延迟方面考虑，互质阵列总延迟数为37，提出的两种阵列设计的总延迟分别为43和49，综上，提出的阵列设计方式在连续延迟和总延迟数量方面均优于互质阵列。而文献[13]的连续延迟优于提出的阵列设计1，但是对比总的延迟数量，提出的两种阵列设计均优于文献[13]。

仿真1 4种阵列在相同信噪比下MUSIC算法的角度估计性能。

由图4可知互质阵列产生的连续延迟个数为21。提出阵列设计1和阵列设计2产生的连续虚拟传感器个数分别29和35。文献[13]阵列产生的连续虚拟传感器为33。假设信号源数为7，信源角度均匀分布于[-30◦，30◦] ，信号源与噪声互不相关，信噪比为SNR=-5 dB，快拍数为T=200，耦合参数c1=0.4ejπ/3，B=100。图5显示了4种方法的信源DOA估计性能。从图中可知，提出的两种阵列均能估计出信源方向信息，文献[13]提出的阵列和互质阵列的角度估计误差较大、存在伪峰，导致角度分辨率低，无法准确估计目标信号源。由式(7)可求得互质阵列和文献[13]提出阵列的耦合泄漏量分别为L1=0.3905和L2=0.5065，而提出的两种阵列耦合泄漏量分别为L3=0.3872和L4=0.3866。因此，文献[13]提出阵列具有较强的耦合效应，导致角度估计性能变差，而互质阵列虽然耦合泄漏量较小，但是由于自由度较低，无法准确估计信源DOA，提出阵列设计方法具有较多的连续延迟和较低的耦合效应，由此带来了目标分辨性提升。

图4 4种阵列设计产生的延迟拓扑

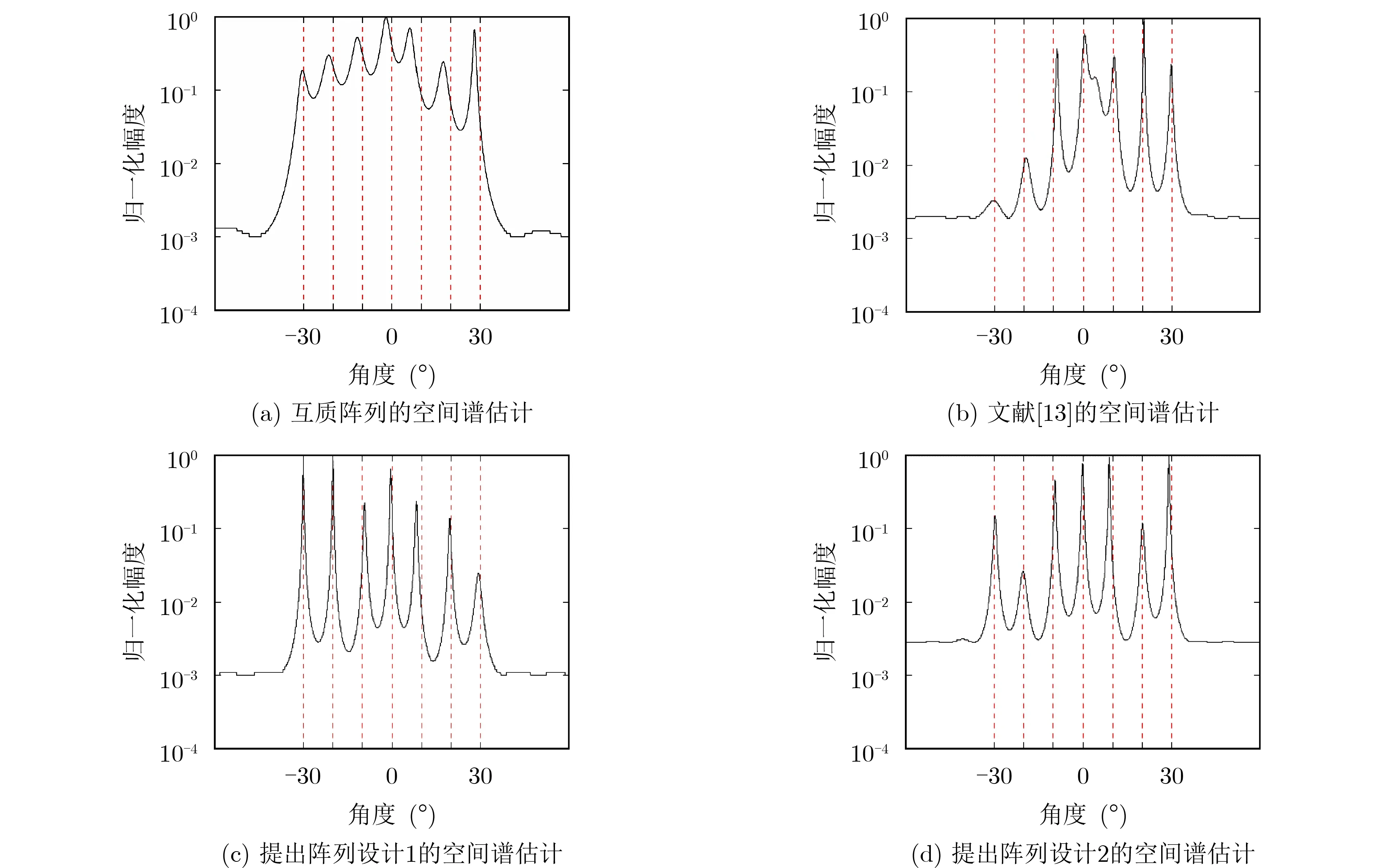
图5 4种阵列MUSIC算法空间谱估计

仿真2 DOA估计均方根误差随信噪比的变化情况。

仿真3 DOA估计均方根误差随快拍数的变化情况。

本次仿真的信噪比为SNR=-5 dB，信源设置与仿真1相同，耦合参数c1=0.1ejπ/3，B=100，300次蒙特卡罗实验取平均形成空间谱曲线，以此验证4种阵列随快拍的变化情况。由图7可知，随着快拍数的增加，4种阵列的均方根误差都在减小，趋势变化相近于CRB曲线，其原因可归结于：随着快拍的增多，协方差矩阵噪声扰动趋于稳定，更有利于参数估计。从图中还可以得出，随着快拍数的增加，提出的阵列结构的DOA估计性能优于互质阵列和文献[13]提出的方法，其性能提升原因为提出阵列的差分共阵具有更多的连续延迟和较低的耦合效应。

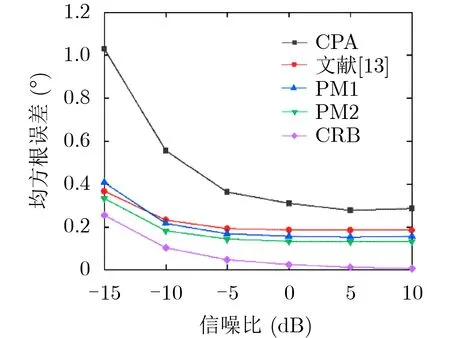
图6 均方根误差随信噪比的变化情况

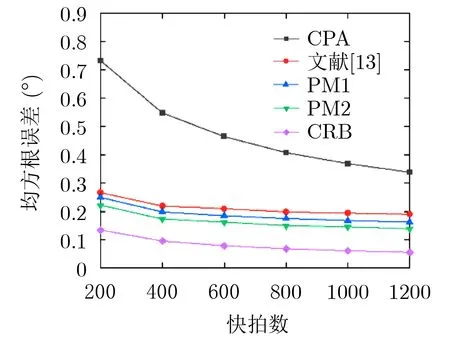
图7 均方根误差随快拍数的变化情况

5 结论

本文通过分析互质阵列阵元位置对差分共阵的影响，从降低硬件成本及简化求解过程考虑，提出了两种基于互质阵列的稀疏设计方法。首先，推得了互质阵列去掉位置为0的阵元，减少了阵列总延迟，但并不改变连续延迟。然后，利用已有的互质阵列孔位关系，移动冗余阵元到孔洞位置形成全新的稀疏阵列，以获得更高的信源估计能力和更好的目标分辨性。最后通过实验仿真，验证提出阵列设计方法相较于对比方法的优越性。下一步，将推广该设计方法到更加复杂的稀疏阵列结构中。