高阶马尔科夫链张量方程的一种反迭代算法

周 艺，吕来水，喻高航

(1.杭州电子科技大学理学院，浙江 杭州 310018；2.南京理工大学计算机科学与工程学院，江苏 南京 210094)

0 引 言

高阶马尔科夫链[1]是一个具有马尔科夫性质的离散时间随机过程。该过程中，在给定当前状态的条件下，未来的状态也依赖于其过去临近几个时刻的状态，而不止当前状态[2]。高阶马尔可夫链应用于许多不同的背景，如DNA序列分析[3]、Multilinear PageRank[4]等。高阶马尔科夫链的极限概率分布问题可转换为求解一个带有约束的转移概率张量方程[5]。2014年,Li等[6]提出求解高阶马尔科夫链的极限概率分布问题的高阶幂法，并在一定条件下建立了算法的收敛性；2019年，Liu等[7]在幂法的基础上，提出了一种非精确的反迭代算法，通过引入松弛参数，在一定程度上提高了算法效率。幂法可看做是固定步长的梯度法，梯度法在机器学习中常见的改进是添加“动量项”[8-9]，这样能够充分利用历史梯度信息，从而改善传统梯度法效率。本文结合动量梯度法，提出一种新的反迭代算法——具有动量项的带位移的反迭代算法(简称Inv-PMM)，并给出算法的收敛性分析和误差估计。

1 预备知识

假设存在一个与时间无关的固定概率pi1i2…im，满足：

0≤ai1i2…im=prob(Xt+1=i1|Xt=i2,…,Xt-m+2=im)≤1

其中，i1,i2,…,im∈〈n〉，称{Xt}为一个m-1阶马尔可夫链。概率ai1i2…im构成的张量=(ai1i2…im)称为转移概率张量，显然≥0且特别地，当m=2时，序列就是一个标准的一阶马尔可夫链，就退化为一个概率转移矩阵。

向量x表示马尔可夫链{Xt}的概率分布向量，文献[6]将高阶马尔科夫链极限概率分布问题近似成如下张量模型：

x=

(1)

2 反迭代动量算法及收敛性分析

2.1 反迭代动量算法

一阶优化中的动量梯度算法主要是在梯度下降算法的基础上添加动量项，从而达到加速优化的效果。基于动量梯度算法的思想，本文提出一种具有动量项的带位移的反迭代算法Inv-PMM用于求解张量方程(1)，算法主要步骤如下。

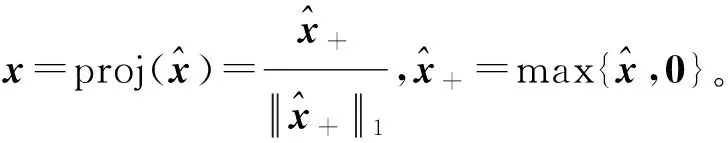
2.2 收敛性分析

为了分析Inv-PMM算法的收敛性，给出如下引理。

引理1[6]如果是一个m阶n维非负转移概率张量，令δm满足：

(2)

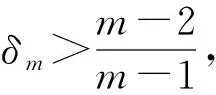
引理2[7]如果是一个m阶n维非负转移概率张量，x,y∈Rn是n维随机向量。则有：

(3)

(4)

(5)

(6)

式中，κm=1-δm，0<κm≤1。

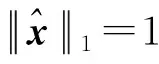
基于上述3个引理，得到Inv-PMM算法的收敛性定理。

定理如果是一个m阶n维非负转移概率张量，满足是方程(1)的解，则对于任意的初始向量x0，当参数满足且算法生成的序列收敛，并且有如下误差界：

(7)

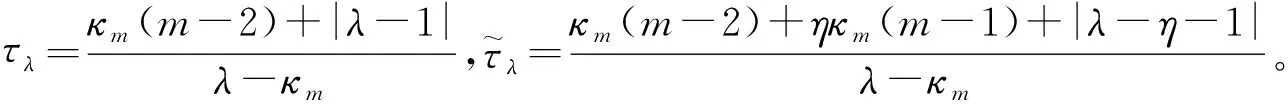
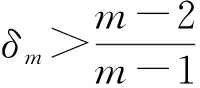
(1)当k不被2整除时，通过Inv-PMM算法步骤1中的(λI-得到：

(8)

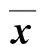
(9)

联立式(8)和式(9)，得：

(10)

由式(3)得：

(11)

令zk-1=(通过式(6)得到：

(12)

则有：

(13)

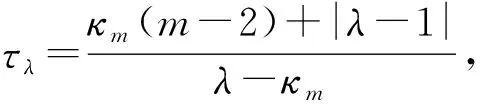
(14)

通过引理3，可得到：

(15)

故：

(16)

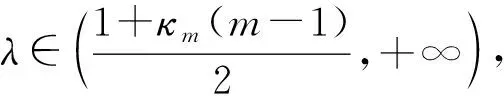
(2)当k被2整除时，Inv-PMM算法的迭代格式可写成：

(λI-

(17)

即：

(18)

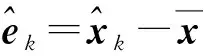
(19)

由式(3)、式(4)、式(6)分别得：

(20)

(21)

(22)

则有：

(23)

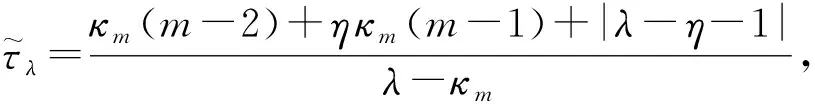
(24)

故：

(25)

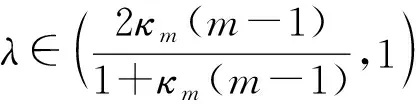
综合上述2种情况，对于∀k=1,2,3,…，由式(16)、式(25)推得：

(26)

3 数值实验

实验在Windows 10操作系统下的MATLAB R2016a中完成，硬件配置为Intel(R) Xeon(R)E-2176M CPU @2.71GHz。

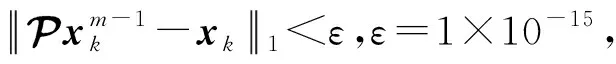
对4个非负不可约转移概率张量的极限概率分布向量进行求解。例1是一个3阶3维张量，来自于文献[10]中的表6；例2是一个4阶3维张量，来自于文献[11]；例3是一个3阶3维张量，来自于文献[12]中的表3；例4是一个4阶4维张量，来自于文献[12]中的表2。实验中，HOPM算法不涉及自由参数的选取，其他3种算法的参数如表1所示。从算法的迭代步数、计算时间及相对残差3个方面进行比较分析，实验结果如表2所示。

表1 不同算法的实验参数

从表2可以看出，4种算法中，Inv-PMM算法的相对范数更小、误差迭代步数更少、运行时间短，说明Inv-PMM算法的收敛速度最快，算法效果最优。

4 结束语

针对高阶马尔科夫链极限概率分布问题，本文提出一种具有动量项的带位移的反迭代算法Inv-PMM，采用周期间隔的动量外推，使得算法生成的序列能够更快地收敛到问题的平稳分布。如何自适应选取位移参数和动量参数是下一步研究重点。