自适应事件触发下网络控制系统鲁棒容错控制

田亦飞，姜偕富，孙国领

(杭州电子科技大学自动化学院，浙江 杭州 310018)

0 引 言

网络控制系统(Networked Control Systems，NCSs)是指通过网络来交换数据的闭环系统。由于NCSs省略了繁杂的布线环节并且容易进行扩展维护，因此在许多领域得到广泛应用[1-2]。但是，随着NCSs自身结构的复杂化，故障的诱导因素也越来越多。容错控制分为被动容错与主动容错。当线性时不变系统执行器故障时，文献[3]给出了被动容错控制器设计方案，对系统进行故障补偿，并优化了系统的性能；针对执行器故障的NCSs，文献[4]给出鲁棒主动容错控制器设计方案。众所周知，NCSs的网络带宽是有限的，周期采样控制将许多不必要的数据纳入传输，造成资源浪费。事件触发机制弥补了周期采样控制的缺点，通过触发条件来筛选可以被释放的信号，实现了信号“按需”发送[5-7]。文献[8]提出一种自适应事件触发机制(Adaptive Event-triggered Mechanism, AETM)，可以根据系统状态自适应调节其触发参数。随后，AETM吸引了众多学者的目光。例如，文献[9]研究了基于AETM非线性网络控制系统H∞跟踪问题；文献[10]研究了基于AETM非线性系统随机故障检测问题，同时通过示例验证了AETM相较于静态事件触发机制可以获得更大的平均发送周期。但是，AETM仍具有一定保守性，如文献[8]中的触发参数取值范围较小，使得AETM的作用未能充分发挥。为了充分利用网络资源，本文将AETM引入具有参数不确定性和执行器故障的NCSs中，设计一种改进的AETM参数自适应律，使得触发参数变化更加灵活，构造一个合适的L-K泛函，并运用Lyapunov稳定性理论，推导出系统稳定的充分条件。

1 问题描述

1.1 系统模型

假设线性系统模型如下：

(1)

1.2 自适应事件触发机制

假设系统(1)中的传感器以固定采样周期h进行采样，将数据单包发送到AETM，采样序列为S1={0,h,2h,…,kh},k∈{0,1,2,3,…}，信号从AETM成功释放的时间序列为S2={t1h,t2h,t3h,…,tkh}，tk∈{0,1,2,3,…}，显然有S2⊆S1。

参考文献[8]，设计如下AETM：

eT(il)Φe(il)≤δ(il)xT(il)Φx(il)

(2)

式中，Φ>0为AETM的权重矩阵，il=tkh+lh，(l=0,1,2,…)为当前采样时刻，tkh为上次信号成功释放时刻，e(il)=x(il)-x(tkh)为当前采样信号减去上次释放的信号。当采样信号不满足式(2)时将被释放。

式(2)中，δ(il)为自适应触发参数，满足

(3)

1.3 基于AETM的闭环NCSs

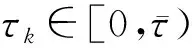
(4)

τ(t)=t-il，t∈Ω

(5)

引入开关矩阵L来描述执行器故障，其模型描述为L=diag{χ1,χ2,…,χm}。其中,

(6)

采用状态反馈策略，系统控制输入为u(t)=Kx(tkh)，t∈Ω。结合式(5)和式(6),u(t)最终表示为：

(7)

结合式(1)和式(7)，得到基于AETM的闭环NCSs模型：

(8)

1.4 相关引理

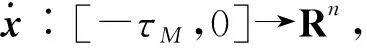
(9)

成立。

(10)

成立。

2 主要结果

2.1 稳定性分析

(11)

式中，

v(t)=F(t)g(t)，t∈Ω

(12)

由式(11)和式(12)可知：

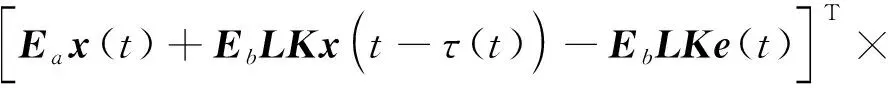
(13)

定理1对于给定标量τm，τM，δM∈(0，1)，矩阵K和L，若存在正定对称矩阵Φ，N，P，S，Qi，Ri，(i=1，2)和标量ε>0，满足如下矩阵不等式

(14)

则闭环NCSs(8)是渐近稳定的，其中

ψ33=Q2-Q1-R1-S，ψ22=δMΦ-2S+NT+N，ψ44=-Q2-R2-S。

证明构建Lyapunov-Krasovskii泛函

(15)

沿着NCSs(11)的动态轨迹对时间t进行求导，得到：

(16)

由引理1可得：

(17)

(18)

由引理2可得：

(19)

结合式(2)，式(16)—式(19)可得：

(20)

Γ11=PA+ATP+Q1-R1-R2+ATΘA，Γ12=PBLK+ATΘBLK，Γ15=PD+ATΘD，

Γ16=-PBLK-ATΘBLK，Γ22=δMΦ-2S+NT+N+(BLK)TΘ(BLK)，

Γ25=(BLK)TΘD，Γ26=-(BLK)TΘ(BLK)，Γ33=Q2-Q1-R1-S，Γ44=-Q2-R2-S，

结合式(13)，运用S-过程，可得：

(21)

对于ε>0，Γ′满足

(22)

2.2 鲁棒容错控制与AETM协同设计

(23)

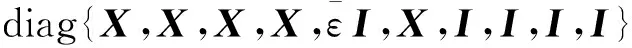
本文给出的触发参数自适应律中，σ1和σ2为关于误差的反正切函数，与文献[8]相比，不再是2个固定标量，建立了触发参数与误差两者间的联系，使得AETM具有更好的灵活性，同时降低了方案的保守性。

3 仿真示例

假设一类闭环网络控制系统模型[14]的参数如下：

针对执行器状态的不同情形，构建如下开关矩阵L：L1=diag{1,1}表示执行器全部正常，L2=diag{0,1}表示执行器1完全失效，L3=diag{1,0}表示执行器2完全失效，L4=diag{0.8,0.2}表示执行器1和执行器2部分失效。

运用Simulink进行仿真，取仿真时长T=30.0 s。执行器故障的情形下，状态响应曲线如图1所示。从图1可以看出，针对具有执行器故障和参数不确定的NCSs，采用本文设计的方案，保证了系统是渐近稳定的，即提高了系统的鲁棒性能，又使得系统具有较好的容错效果。

图1 状态响应曲线

当NCSs引入AETM后，在30 s内传输了38个采样数据，仅占周期采样控制(h=0.1 s,30.0 s内传输300个数据)的12.7%。采样信号释放时刻与释放间隔如图2所示，δ(il)自适应调节曲线如图3所示。

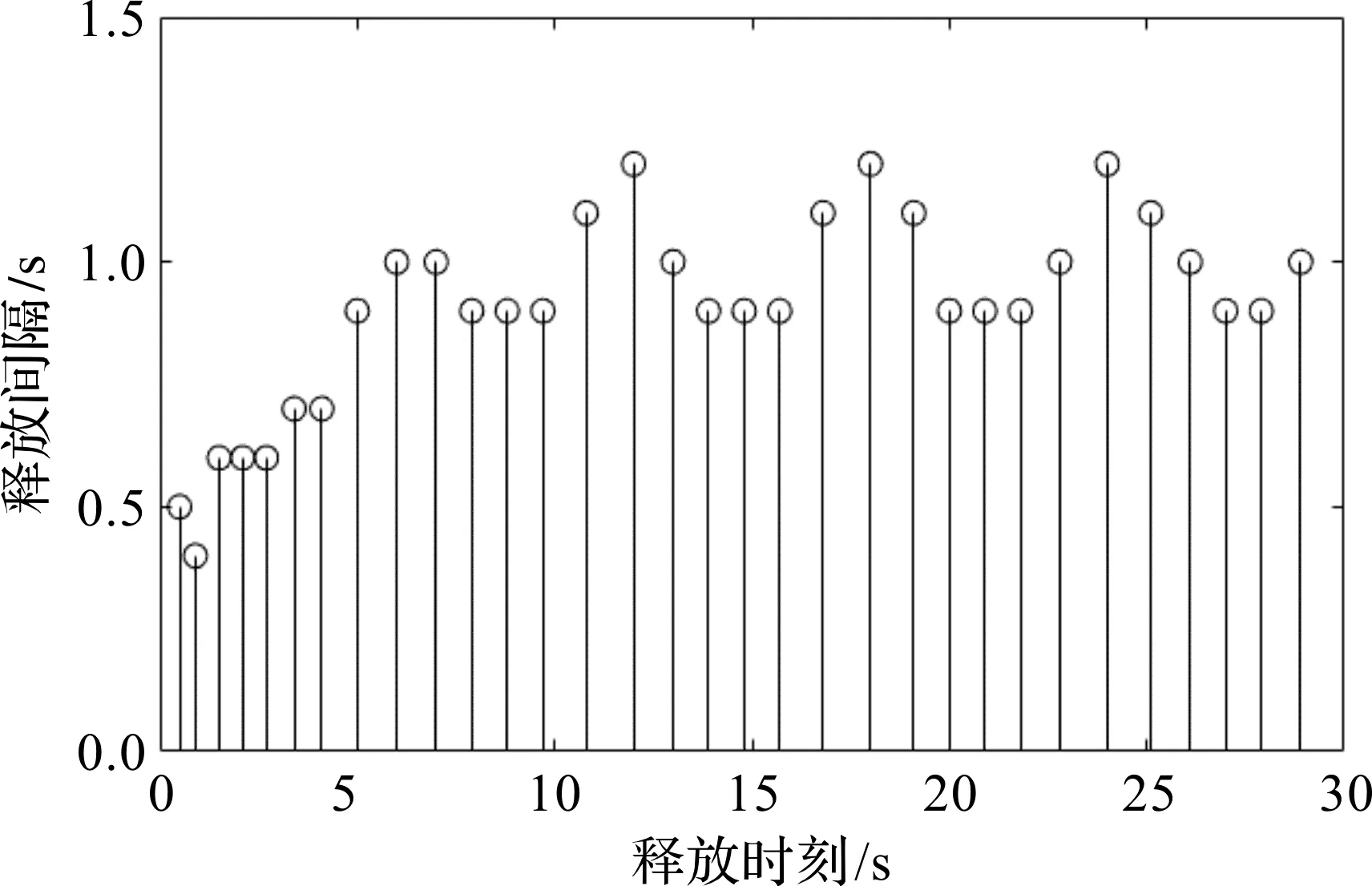
图2 采样信号释放时刻与释放间隔图

图3 δ(il)自适应调节图

从图2可以看出，AETM有效降低了信号的传输频率，节约了网络资源。从图3可以看出，δ(il)不再是一个标量，而是随着系统状态的变动而改变。为了说明本文AETM的优越性，将信号发送频率同其他通讯机制进行比较，结果如表1所示。

表1 不同通讯机制下的信号发送频率

由表1可知，在保证系统稳定性能的前提下，改进后的AETM可以发送更少的数据，提高了平均发送周期。综上分析，本文设计的方案不仅可以有效应对传感器故障问题，同时还可以更加充分地利用网络资源。

4 结束语

针对具有参数不确定性和执行器故障的网络控制系统，本文提出一种鲁棒容错控制与AETM协同设计方案。对现有的AETM进行改进，使得触发参数变化更加灵活。在不等式放缩过程中，运用倒凸组合技术，得到满足鲁棒容错性能的控制器参数，降低了方案的保守性。但是，本文设计的方案没有考虑非线性因素，下一步计划将此方案扩展到非线性网络控制系统中。