基于密钥传递的加密数据去重技术

张 品，李佳楠

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

0 引 言

数据去重技术又称重复数据删除技术，是一种云端数据压缩技术，即每个数据只保留一份，并为拥有相同数据副本的授权用户创建访问链接，大大节省了网络带宽和存储空间[1]。随着信息安全问题日益凸出，用户对数据隐私越来越重视，不再直接将数据外包到云服务器上，而是将数据加密后上传到云服务器[2]。由于不同用户选择不同的密钥进行加密，导致相同数据被加密成不同的密文，给数据去重技术带来困难[3]。Douceur等[4]首次提出了收敛加密(Convergent Encryption，CE)用于平衡数据隐私性和去重高效性，但该方法的密钥过于依赖明文数据，在信息熵较低时，容易遭受离线字典攻击。在CE算法的基础上，Bellare等[5]提出了消息锁加密(Message-Locked Encryption，MLE)，其本质与CE算法相同，并不能解决语义安全问题。Bellare等[6]改进了MLE算法，提出交互式MLE(interactive MLE，i-MLE)，采用同态加密保证了内容的语义安全，但计算开销过大。Puzio等[7]提出ClouDedup方案，通过引入1个额外的服务器和元数据管理器(Metadata Manager，MM)来增强数据的机密性，但要求第三方服务器完全可信，比较难实现。Bellare等[8]提出DupLESS方案，数据的加密密钥不再由明文导出，虽然能抵抗蛮力攻击，但需要保证密钥服务器(Key Server, KS)不能与云服务器合谋。Wang等[9]提出一种密文安全去重方案，借助1个索引服务器(Index Sever，IS)进行密钥的传递，使得拥有相同数据副本的用户共享同一密钥，实现了对加密数据的去重，但因为第三方服务器在实际布置中存在技术限制，易成为系统瓶颈[10-11]。

针对现有数据去重方案存在的问题，本文提出一种改进的加密数据去重方案，不需要其他用户的辅助，简化了密钥传递的过程。通过添加额外的安全机制，使得非授权用户无法下载数据，降低了标签生成过程的计算开销，执行效率更高。

1 预备知识

给定G，GT是2个阶数为p的乘法循环群，g是群G的生成元，定义双线性映射e∶G×G→GT具有以下性质[12-13]：

(1)双线性：对于任意的a,b∈Zp,u,v∈G，都有e(ua,vb)=e(u,v)ab。

(2)非退化性：对于任意的g∈G，都有e(g,g)≠1。

(3)可计算性：对于任意的的u,v∈G，e(u,v)是可计算的。

2 方案模型和定义

2.1 方案模型

本文提出的基于密钥传递的加密数据安全去重方案主要考虑用户和云服务器两大实体。将数据外包到云服务器中以节省本地存储空间和成本投入。为了保证数据的隐私性，选择在进行数据外包之前进行加密。用户(User，U)分为2类，一类是数据的初始上传者，另一类是数据的后续上传者。云服务器(Cloud Service Provider，CSP)主要提供数据存储服务。

2.2 方案设计

本文通过双线性映射来构建方案，在不泄露明文信息的前提下，云服务器可以验证加密数据是否来自同一明文。加密密钥不再是由明文确定性生成，而是由用户随机选择的，密钥传递过程中无需可信第三方服务器和实时在线用户的参与。通过Elgamal算法[14]进行密钥传递，保证传递过程的安全性。方案分3个阶段执行，分别为系统初始化、文件上传、文件下载。

2.3 符号定义

本文所用到的符号定义如表1所示。

表1 符号定义

2.4 系统初始化

在初始化阶段，由系统定义2个阶数为大素数p的乘法循环群G，GT，g为群G的生成元，定义双线性映射e∶G×G→GT。为Elgamal加密算法定义1个阶数为大素数q的乘法循环群G1，g1是该群的1个生成元。h1∶{0,1}*→Zp,h2∶{0,1}*→Zq是2个安全抗碰撞的哈希函数[15]，H(·)是1个SHA256哈希函数。E(·)和D(·)表示对称加密和对称解密过程，Enc(·)和Dec(·)表示Elgamal算法的加密和解密过程。CSP生成(MK，SK)作为系统的主公钥和主私钥，并为每个加入系统的用户生成唯一的身份标识ID以及公私钥对(sk，pk)。

2.5 文件上传

在文件上传阶段，主要分为2种情形：一是文件第1次上传，二是文件的重复上传。

情形1假设用户A作为数据F的初始上传者，执行流程如下：

(1)生成密钥KenGen(x,p,g)→KA。用户A随机选择1个x∈Zp，计算KA=gx作为自己的加密密钥。

(2)生成去重检测标签DedupToken(ti,F)→Tf。用户输入参数ti和文件数据F，输出检测标签。具体生成为Tf=(gti,gtih1(F))，其中ti是1个随机数，并且ti∈Zp。

(3)加密数据E(KA,F)→CF。用户使用自己的密钥KA对数据F进行加密，生成密文CF。

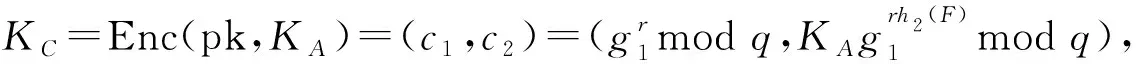
(5)生成密文标签TokenGen(CF)→TC。用户将加密后的数据密文CF作为输入，经H(CF)后生成标签TC，用来验证标签和密文的一致性。

(6)上传数据Upload。用户将身份标识ID、数据密文CF、去重标签Tf、密钥密文KC以及密文标签TC一同上传到CSP中，用户自己只需保存h2(F)、身份标识ID和Tf用于下载数据解密时使用。

情景2假设用户B作为数据F的后续上传者，执行流程如下：

(1)生成密钥KeyGen(y,p,g)→KB。用户B随机选择1个y∈Zp，计算KB=gy作为自己的加密密钥。

(2)生成去重检测标签DedupToken(tj,F)→Tf。用户输入参数tj和文件数据F，输出检测标签。具体生成为Tf=(gtj,gtjh1(F))。将检测标签上传到CSP中，由CSP对比云服务器中已经存在的标签，计算e(gti,gtjh1(F))和e(gtj,gtih1(F))是否相等，若两者相等则表示该数据已经存在，不需要用户再次上传，需要进行所有权验证。

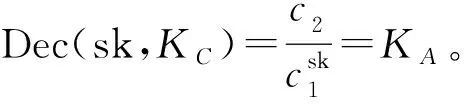
(4)所有权证明阶段(Proof of Ownership，POW)[16-17]。为了确保用户确实持有与其上传的标签相对应的完整数据，由CSP和用户执行POW交互协议，主要分为3个步骤。

①生成挑战信息POWChal，由CSP执行。CSP对存储的加密数据进行固定分块，即C={C1,C2,C3，…,Ci}，随机抽取若干个块信息，将块的位置信息C0={C1,C2,…,Ck}作为挑战信息以加密认证的方式Enc(pkUB,C0)发送给用户。

②生成挑战证据POWPro，由用户执行。用户接受到CSP的挑战信息后，先用自己的私钥skUB解密得到C0。根据得到的挑战信息集合计算Hpro={H(C1),H(C2),…,H(Ck)}，并按照一定的顺序采用加密认证的方式Enc(MK,Hpro)将挑战证据返回给CSP。

③验证挑战信息POWVer，由CSP执行。CSP接受到用户的证明信息后，使用自己的私钥SK通过相同的方式对密文数据块进行计算，将计算的结果与Hpro进行对比，如果相等则用户通过POW证明，将用户的身份标识ID添加到授权用户列表中；否则用户挑战失败。

2.6 文件下载

用户需要下载数据F时，先向CSP发送下载请求，再将身份标识ID和检测标签Tf一同发送给CSP。CSP收到请求后，首先检测Tf所对应的文件是否存在，如果存在则进一步检查该用户的ID是否在文件的授权列表中，只有确定该用户是数据F的拥有者后，才能将密钥密文KC和数据密文CF返还给用户。

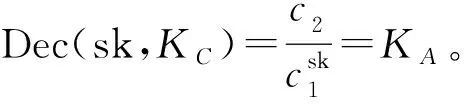
(2)解密数据D(KA,CF)→F。通过数据密钥运行解密算法得到数据F。

3 实验结果与分析

3.1 实验环境

实验在1台联想Lenovo Y700计算机上进行，操作系统为Windows 10，配置为Intel(R)Core(TM)i5-6300HQ CPU@2.30Hz 2.30GHz，内存为8 GB，编程语言为Java，哈希函数采用SHA-256，加密算法为对称加密AES-256，双线性映射构造从JPBC库[18]中调取，所使用的加密算法均来自OPENSSL函数库。

3.2 计算开销

为了对方案的计算开销有一个定量的描述，对各种运算采用符号表示。Hash表示SHA-256，Exp和XOR分别表示指数运算和异或操作，PE表示双线性映射计算，Elgamal表示执行1次Elgamal算法。以1个数据初始上传者为例，将本文方案和文献[9]方案在标签生成阶段和密钥传递阶段所需的执行操作进行对比，结果如表2所示。

表2 不同方案在各阶段的执行操作

随机生成不同大小的文件，分别为2 MB，4 MB，8 MB，16 MB，32 MB，64 MB和128 MB，使用本文方案和文献[9]方案进行文件上传，取10次实验的平均值。不同大小的文件在标签生成阶段的计算开销如图1所示。

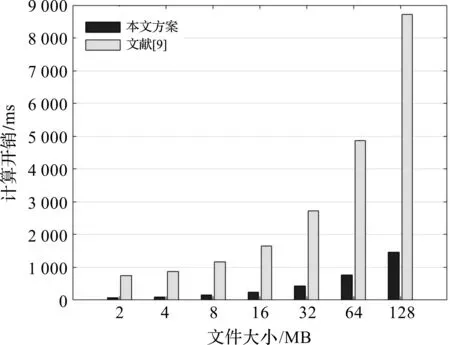
图1 标签生成阶段中，不同方案的计算开销

由图1可知，在标签生成阶段，本文方案的计算开销远小于文献[9]方案，这是因为文献[9]中标签生成采用Merkle哈希树构造，文件的分块耗费了大量时间，同时，文献[9]方案采用1 024个叶子节点，需要计算2 047次哈希运算；而本文方案计算标签时，只需要1次哈希运算和2次指数运算，运算量大大减少。

密钥分发阶段中，本文方案与文献[9]方案的计算开销如表3所示。

表3 密钥分发阶段中，不同方案的计算开销 单位：ms

结合表2、表3和图1可以看出，本文方案的计算开销要小于文献[9]的去重方案。

本文方案中，数据初始上传者和后续上传者的总计算开销如图2所示。从图2可以看出，与数据初始上传者相比，当上传的数据已经存在时，数据后续上传者需要与CSP执行POW来证明自己的数据拥有权，计算开销要大于数据初始上传者。

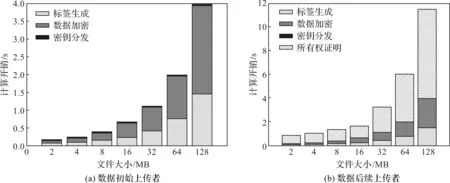
图2 不同用户的总计算开销对比

3.3 其他开销

除了计算开销，在执行数据去重的过程中还产生额外的通信开销和存储开销。对于数据F，CID，CC，CK分别表示用户标识大小、密文大小、密钥密文大小，CT，Csk，CS分别表示去重标签大小、用户私钥大小、随机密钥大小，Ch，CP，CV分别表示数据的哈希值、挑战信息大小、证明信息大小，Ct表示系统参数。

通信开销主要产生于数据上传、数据下载阶段。本文方案和文献[9]方案的通信开销如表4所示。

表4 不同方案的通信开销

从表4可以看出，相较于初始上传者，数据后续上传者不需要重复上传数据密文，节省了通信开销。在数据的后续上传阶段，相较于文献[9]方案，本文方案有额外的用户标识以及密钥密文的开销，这是因为文献[9]方案通过KS实现了对加密密钥的管理，而本文方案则需要数据后续上传者向CSP获取密钥。因此，在数据后续上传阶段，本文方案的通信开销要略大于文献[9]。

存储开销主要包括云服务器端、用户端和额外服务器端。N表示合法用户数量，本文方案和文献[9]方案的存储开销如表5所示。

表5 不同方案的存储开销

从表5可以看出，本文方案和文献[9]方案均实现了对加密数据的安全去重，但本文方案没有可信第三方服务器的参与，不会出现服务器单点故障等问题，可靠性更强。

4 结束语

本文提出一种基于密钥传递的无可信第三方加密数据去重方案，实现了对加密数据的高效去重，摆脱了第三方服务器的束缚，提高了方案的实用性，计算开销更少、执行效率更高。本方案中，数据的加密密钥由用户随机选取，避免了CE算法中易遭受离线字典攻击的问题。但是，本文研究在数据去重的粒度方面以及所有权变更方面考虑不全，下一步将着重研究数据块级别的去重，并针对用户数据所有权变更提出相应的应对对策。