基于自适应观测器的直升机系统故障估计

陆孟洁， 王天真， 祝小元

(1.上海海事大学，上海 201000； 2.东南大学，南京 211000)

0 引言

无人机由于在军事和民用领域的广泛应用而备受关注[1]。与固定翼无人机相比，旋翼无人机具有体积小、悬停时间长和飞行灵活等特点[2]。因此，直升机作为一种典型的旋翼无人机，被广泛用于执行搜索救援、线路巡检、农业植保等特定任务[3-4]。直升机作为高度复杂且不稳定的系统，任何系统故障都会造成严重的后果。因此，为了提高直升机系统的可靠性和安全性，对其进行故障估计研究变得越来越重要[5-6]。

目前，已经有很多故障估计方法被提出，如未知输入观测器[7]、鲁棒观测器[8]、学习观测器[9]和自适应观测器[10]等。其中，自适应观测器由于设计简单且适用于各种不同的系统，受到越来越多研究者的关注，并且取得了一系列研究成果。文献[11]首次提出自适应观测器并将其应用于线性系统执行器故障估计研究；文献[12]考虑系统存在的时间延迟，设计了自适应观测器对系统执行器故障进行估计；文献[13]将自适应观测器应用于马尔可夫跳变系统，对执行器故障和传感器故障进行同时估计；为了提高传统比例型自适应观测器的动态性能和对外界扰动的鲁棒性，文献[14]在观测器结构中引入输出误差的微分项，提出了比例-微分型自适应观测器；进一步，为了改进观测器的瞬态响应，文献[15]提出了一种改进的鲁棒自适应观测器。

对于三自由度直升机系统的故障估计，文献[16]对4种常用的故障观测器进行了仿真和实验验证，对比分析了4种观测器的故障估计性能，但没有考虑直升机系统的非线性；文献[17]基于直升机的非线性模型，设计了一个未知输入观测器实现执行器故障估计，并且将故障估计值用于容错控制，但其只考虑了缓慢变化的故障，没有对突变故障进行研究；文献[18]针对直升机系统的执行器故障和传感器故障设计了一个自适应观测器，可以很好地实现故障估计，但其考虑的故障形式都为方波形式，没有考虑时变故障;文献[19]设计了一个自适应滑模观测器对执行器故障进行估计，但其自适应率只用到输出误差项，没有用到输出误差的微分项，导致其故障估计性能较差。

本文针对三自由度直升机，对基于自适应观测器的故障估计进行研究。首先，设计了比例型自适应观测器对直升机的执行器故障进行估计，在此基础上又提出了比例-微分型自适应观测器，最后，通过三自由度直升机系统对所设计的故障观测器进行仿真验证。结果显示，比例-微分型自适应观测器具有更高的故障估计精度和速度。

1 三自由度直升机模型

Quanser公司的3-DOF直升机平台如图1所示。

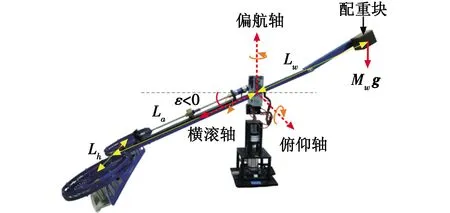
图1 Quanser的3-DOF直升机平台Fig.1 Quanser’s 3-DOF helicopter platform

本文仅考虑直升机俯仰轴和横滚轴，动力学方程为

(1)

式中：ε为俯仰角；p为横滚角；Jε和Jp分别为两个轴的转动惯量;Kf为螺旋桨升力常数;La为旋转轴到机体的距离;Lh为横滚轴到电机的距离;mh为直升机等效质量;Vf与Vb分别为前、后电机的电压值;ωε和ωp分别为两个轴的模型不确定性。

直升机模型可重新描述为

(2)

式中：bε=KfLa/Jε;bp=KfLh/Jp，dε=wε/Jε+bε(cosp-1)(Vf+Vb)，dp=wp/Jp分别表示两个轴的等效扰动项，且非线性项f1(x)=-mhgLacosε/Jε。

根据以上定义，建立其状态空间故障模型为

(3)

假设1 假设非线性项f(x,t)满足Lipschitz非线性条件，即‖f(x1,t)-f(x2,t)‖≤κ‖x1-x2‖,κ是Lipschitz常数。

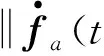
引理1对于任意适当维数的矩阵X,Y，存在一个对称正定矩阵H使如下条件成立：XTY+YTX≤XTHX+YTH-1Y。

2 自适应观测器设计

2.1 比例(P)型自适应观测器

对于式(3)的系统，构造P型自适应观测器,即

(4)

定义状态估计误差、输出估计误差和故障估计误差为

(5)

定理1对于式(3)系统，如果存在对称正定矩阵P和G，适当维数矩阵W和R，以及标量ε1>0满足条件

(6)

BTP=RC

(7)

证明 根据式(3)和式(4)，可以得到

(8)

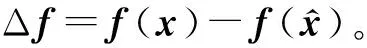
选取Lyapunov函数

(9)

则V对时间的导数为

(10)

将式(7)代入式(10)可得

(11)

由假设2可得

(12)

根据引理1可得

(13)

将式(12)和式(13)代入式(11)，可得

(14)

为了保证故障观测器对外部扰动的鲁棒性能，定义H∞性能如下

(15)

由零初始条件V(0)=0,V(∞)>0，可得

(16)

式(16)中的积分项可以写为

(17)

如果不等式

(18)

由于式(18)条件不是标准的LMI形式，无法用LMI工具箱进行求解。运用Schur补引理，并且令W=PL，式(18)可以等效为式(6)的形式。证明完成。

2.2 比例-微分(PD)型自适应观测器

对于式(3)系统，构造PD型自适应观测器

(19)

式中所有变量与第2.1节中的变量相同。

定理2对于式(3)系统，如果存在对称正定矩阵P和G，适当维数矩阵W和R，以及标量ε1>0，ε2>0满足式(7)和如下条件

(20)

式中，N2=ATP+PA-CTWT-WC+(κ2/ε1+κ2/ε2)I+CTC，N3=CTWTB-ATPB，N4=G-2BTPB,则有如式(19)的PD型自适应观测器，其中增益矩阵为L=P-1W。

证明 考虑式(9)中选取的Lyapunov函数，则V对时间的导数为

(21)

将式(7)代入式(21)可得

(22)

根据引理1可得

(23)

将式(12),(13)和式(23)代入式(22)，可得

(24)

同样,为确保故障观测器对外部扰动的鲁棒性能，定义和式(15)相同的H∞性能，由零初始条件可得

(25)

式(25)中的积分项可以写为

(26)

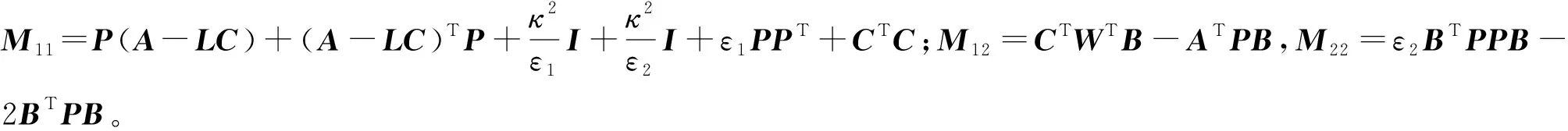
如果不等式

(27)

同理，运用Schur补引理，并且令W=PL，式(27)可以等效为式(20)的形式。证明完成。

注1 由于式(7)条件不是标准的LMI形式，不便于求解，可将以上的式(7)条件转化为不等式

(28)

式中，μ是一个充分小的正数。

注2 为了保证所构造的两个故障观测器的收敛速度，将矩阵(A-LC)的所有特征值配置在一个圆形区域D(α,r)。因此，可以在定理1和定理2中加入条件约束

(29)

式中，α和r分别是圆形区域的圆心和半径。

3 仿真验证

本文基于Matlab/Simulink的三自由度直升机仿真系统，针对突变型故障和时变型故障，对构造的两个故障观测器进行仿真验证，并且通过对比分析其性能。

选择参数ε1=ε2=0.001，μ=10-6，γ=2，ρ=40，α=-10，r=10。由不等式(6)，(28)和(29)，可得P型自适应观测器增益矩阵为:

由定理2可得PD型自适应观测器增益矩阵为:

3.1 突变型执行器加性故障估计

当直升机系统存在突变型故障时，假设两个故障分别为

(30)

(31)

图2的故障估计结果显示，在直升机系统存在突变故障时，P型自适应观测器在稳定情况下可以实现准确的故障估计，但是在故障突变时刻，需要经过0.4 s才能收敛到故障参考值，且存在较大的超调量，估计性能比较差。然而，PD型自适应观测器在整个过程都能实现精确的故障估计，故障估计性能明显优于P型自适应观测器。

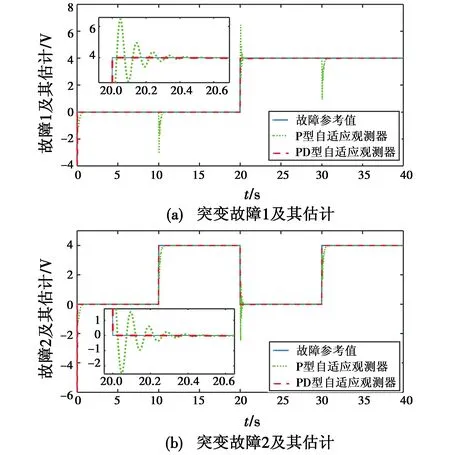
图2 两个突变故障及其估计Fig.2 Two abrupt faults and their estimations

3.2 时变型执行器加性故障估计

当直升机系统存在时变型故障时，假设两个故障分别为

(32)

fa 2=2sin 2πt0≤t≤40

(33)

图3的故障估计结果显示，在直升机系统存在时变故障时，P型自适应观测器的估计效果比较差，故障1和故障2会相互影响，估计结果中存在较大的稳态误差。然而，PD型自适应观测器可以很好地实现两个故障的估计，估计速度快并且稳态误差很小。

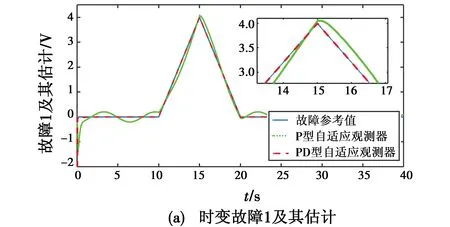
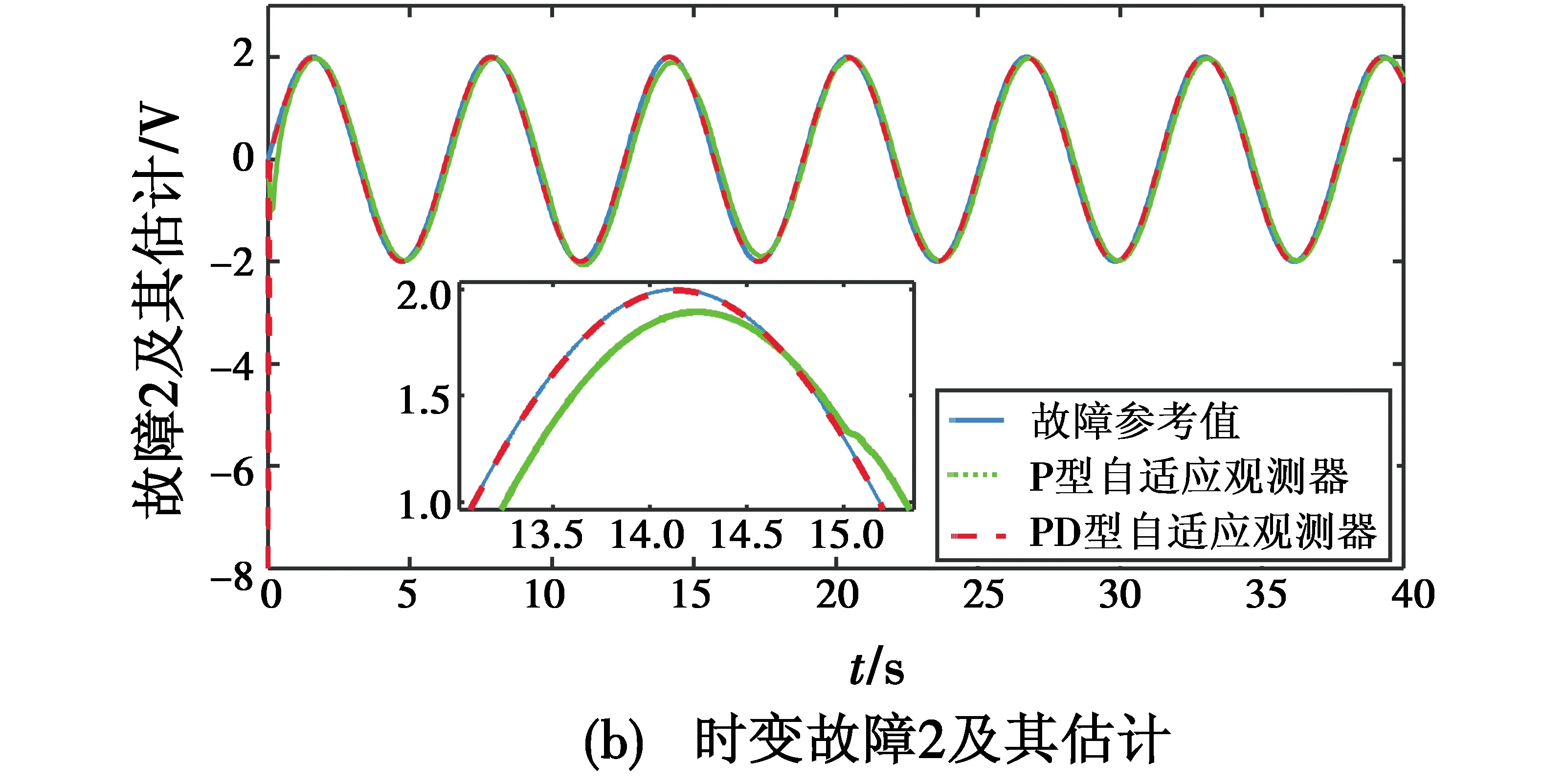
图3 两个时变故障及其估计Fig.3 Two time-varying faults and their estimations

4 结束语

本文针对三自由度直升机，对基于自适应观测器的故障估计问题进行研究。首先，建立三自由度直升机的非线性模型，提出了基于比例型自适应观测器的故障估计方法，在此基础上又构造了比例-微分型自适应观测器，最后，通过三自由度直升机系统对所设计的故障观测器进行仿真验证。结果表明，与比例型自适应观测器相比，比例-微分型自适应观测器显著提高了故障估计精度和速度。