基于对局迭代的无人机空战博弈研究

刘昊天， 王玉惠， 陈 谋， 张逸航

(南京航空航天大学自动化学院，南京 211000)

0 引言

近年来，无人机因拥有低风险、低成本、高性价比、高过载以及优越的隐身性能和灵活性等优点而备受青睐，在战场上发挥的重要作用也日益凸显[1-2]。为进一步提升无人机的空战性能，在建立精确的空战模型的基础上研究先进的空战决策方法对于保证无人机空战的优势具有重要意义。

无人机作为未来空中战场的主要作战单元，攻防决策是其作战必备的功能之一，相关的研究成果促进了空战态势评估与决策的进一步发展[3-6]。文献[4]针对战斗机的超视距协同空战建立了改进的非参量法的态势评估模型，然后将各种威胁函数加权求和得到总体威胁态势函数，为无人机空战决策提供技术参考；文献[5]建立了超视距空战能力层次结构体系模型，根据空战目标分配模型通过遗传算法解得决策结果；文献[6]以多机协同空战的目标分配问题为研究对象，构建攻击优势矩阵，建立整体优势函数，进行目标均衡和任务均衡分配，提出了一种改进的遗传算法用于解决协同空战的目标分配并进行决策。近年来，在上述研究成果[3-6]的基础上，为进一步提升决策性能，很多学者考虑引入博弈论来开展无人机空战决策研究[7-9]，其基本思想是综合考虑敌我双方的态势通过博弈得出纳什均衡值，从而使得决策结果更加符合实际的空战。文献[7]建立了多无人机空战博弈模型，给出了博弈支付矩阵，并且利用量子粒子群算法解出了空战博弈的纳什均衡解；文献[8]利用区间数研究不确定信息下的无人机攻防博弈，根据敌我双方各个作战参数的区间信息，建立不确定敌我双方攻防对抗的博弈模型，利用区间可能度公式，采用线性规划法求解纳什均衡值；文献[9]将粒子群算法与区间数多属性排序方法相结合，给出基于不确定信息下博弈纳什均衡求解方法。目前，这些关于多无人机空战博弈决策问题的研究虽然已经取得了一些成果[7-9]，但未能充分体现博弈双方的对抗，另外，所采取的寻优算法，如遗传算法，粒子群算法等，都有易陷入局部最优等问题亟待解决。

综上分析，本文基于对局迭代针对多无人机协同空战博弈决策问题开展研究。首先，通过敌我双方作战态势和效能参数信息，利用矩阵对策法建立敌我双方对抗支付博弈模型与支付矩阵；然后，利用对局迭代求解空战博弈混合策略的纳什均衡解；最后，通过实例仿真验证了所提方法的有效性。

1 无人机空战优势函数

1.1 无人机空战态势优势函数

在空战中，无人机通过机载目标探测传感器和接收到的其他无人机、预警机或地面站等探测到的目标信息[10]对敌方目标进行定位与识别。

为便于分析，以我方a机与敌方b机为例给出单对单对抗的空战态势如图1所示。

图1 无人机单对单对抗态势图Fig.1 The confrontation situation of a single UAV vs a single UAV

图1中：rab为我方第a架无人机与敌方第b架无人机之间的距离；va和vb分别为我机和敌机速度；ha和hb分别为我机和敌机的高度；φab为我方第a架无人机相对敌方第b架无人机的提前角；qab为敌方第b架无人机相对我方第a架无人机的进入角。

角度优势Waab表示为[11]

(1)

由式(1)可知，当我方无人机尾随敌方无人机时，我方的角度优势最大，当敌方无人机尾随我方无人机时，我方角度优势最小，符合实际空战情况。

速度优势Wvab表示为[7]

(2)

当无人机速度快于对方时，会获得速度优势。

距离优势Wrab表示为[7]

Wrab=e-((rab-R0)/σ)2

(3)

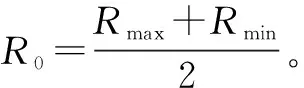
高度优势Whab表示为[11]

(4)

式中，hab是我方无人机与敌方无人机的高度差，我方无人机在敌方无人机上方时将获得高度优势，与实际情况相符。

综合角度、速度、距离和高度优势函数，每架无人机空战整体态势优势函数Wsab可表示为

Wsab=k1Waab+k2Wvab+k3Wrab+k4Whab

(5)

式中，k1～k4为加权系数，且k1+k2+k3+k4=1。

1.2 无人机空战效能优势函数

无人机空对空作战效能优势指数C主要选用5个因素来衡量无人机的空对空作战能力，其算式为

C=[ln(∑A1+1)+ln(∑A2)]ε1ε2ε3

(6)

式中：A1为武器杀伤力参数；A2为探测能力参数；ε1为生存力系数；ε2为航程系数；ε3为电子对抗系数。由于式(6)计算出的空战效能指数与之前得出的空战态势指数量级差别较大，需要进一步处理。为使空战效能指数的值处于[0,1]区间内，重新定义空战效能优势函数WCab为

(7)

式中，Ca和Cb分别为我机和敌机的空对空效能指数。

1.3 无人机空战支付矩阵

每架无人机空战综合优势函数可表示为空战态势优势函数Wsab与空战效能优势函数WCab的加权和。我方每架无人机空战的综合优势函数u1ab表示为

u1ab=l1Wsab+l2WCab

(8)

式中，l1和l2为加权系数，且l1+l2=1。同理可得敌方空战总体优势函数u2ba。

多无人机空战博弈支付矩阵A定义如下

(9)

式中:ai j为我方无人机采取αi策略且敌方无人机采取βj策略时我方无人机的收益;m和n分别为我方无人机策略数量与敌方无人机策略数量。

当我方选取策略αi时，我方获得收益gi为

(10)

当敌方选取策略βj时，敌方获得收益tj为

(11)

所以我方无人机获得总收益ai j为

ai j=gi-tj

(12)

其中:p为我方无人机数量;l为敌方无人机数量;xab，yba分别为二值决策变量，xab=1表示我方第a架无人机攻击敌方第b架无人机，xab=0表示我方第a架无人机没有攻击敌方第b架无人机，yba=1表示敌方第b架无人机攻击我方第a架无人机，yba=0表示敌方第b架无人机没有攻击我方第a架无人机；xabαi，ybaβj分别为当我方选取策略αi、敌方选取策略βj时xab与yba的具体取值。

2 多无人机空战博弈模型

本文仅讨论无人机空战博弈策略集。

2.1 无人机空战博弈纯策略集

在敌我双方空战中，将我方和敌方无人机分别看作博弈对抗的两个局中人[12-13]，多无人机空战博弈模型矩阵对策Q可表示为

Q=(S1,S2;A)

(13)

式中：S1={α1,α2,…,αm}，为我方无人机的纯策略集；S2={β1,β2,…,βn}，为敌方无人机的纯策略集；A=(ai j)m×n，为博弈支付矩阵。在纯策略博弈的情况下，往往不存在一个双方均可接受的平衡局势，所以在情况复杂的空战环境下研究空战博弈问题只使用纯策略集往往无法求出纳什均衡解，为此引入混合策略集[14-15]。

2.2 无人机空战博弈混合策略集

在博弈中，若不存在一个双方均可接受的平衡局势，可以给出一个选取策略的概率分布，我方无人机以概率{x1,x2,…，xm}选取纯策略{α1,α2,…,αm}，敌方无人机以概率{y1,y2,…，yn}选取纯策略{β1,β2,…,βn}。记

(14)

(15)

(16)

式中，E(x,y)为我方无人机的期望支付函数，此时的矩阵对策记成

(17)

式中，Q*为Q的混合扩充。

3 无人机空战博弈求解

3.1 混合策略纳什均衡

由式(17)可知，Q*是我方和敌方无人机的一个混合策略，如果两个局中人均按照“从最不利的情形中选取最有利的结果”的原则[16]，则我方无人机可保证自己的支付的期望值不少于

(18)

敌方无人机可保证所失的期望值至多是

(19)

Q*存在纳什均衡解的充分必要条件为

(20)

式中，VG为博弈Q*的值。则称满足式(20)的(x*,y*)为Q*在此混合策略中的纳什均衡解。

E(x,y*)≤E(x*,y*)≤E(x*,y)。

(21)

当我方无人机取纯策略αi、敌方无人机取混合策略y时，记我方相应的支付函数可表示为

(22)

同理，当我方无人机取混合策略x，敌方无人机取纯策略βj时，我方相应支付函数为

(23)

综合式(22)～(23)，可得

(24)

E(i,y*)≤E(x*,y*)≤E(x*,j)

i=1,2,…，m，j=1,2,…,n。

(25)

这样就可以把要验证无限个(不可数)不等式的问题转化为只需要验证有限个不等式的问题，从而使后面的研究大大简化。

相应地，此时博弈Q*的值VG还可表示为

(26)

3.2 基于对局迭代的博弈纳什均衡值求解

基于对局迭代的博弈纳什均衡值求解过程如图2所示。

图2 对局迭代整体流程图Fig.2 Flow chart of game iteration

对局迭代法是求解博弈问题纳什均衡值的一种有效方法，其基本思想是：多次博弈时，在每局博弈中，我方无人机和敌方无人机都选取一个使对方获得最不利结果的纯策略[17]，即在第t+1局中，我方无人机选取纯策略使得敌方无人机前t局的累计所失为最多，而敌方无人机选取纯策略使前t局我方无人机的累计所得为最少。

具体做法是：在第一局博弈中，我方无人机和敌方无人机都任意选取一个策略，设我方无人机选取策略αi1，敌方无人机选取策略βj1，假设博弈已经进行了t局，k=1,2,…,t，这时,我方无人机已经选取的策略序列是αi1,αi2,…,αit，敌方无人机已经选取的策略序列是βi1,βi2,…,βit，在第t+1局中，我方无人机将选取策略αit+1，使得

(27)

敌方无人机选取策略βjt+1，使得

(28)

(29)

(30)

当局数t足够大时，序列{xt}的每个点都是我方无人机的最优策略，序列{yt}的每个点都是敌方无人机的最优策略。

根据式(26)，(25)，(22)和(23)，从而有

(31)

(32)

所以有

(33)

(34)

因此，若记

(35)

(36)

综上所述，xt和yt可分别作为我方无人机和敌方无人机的近似最优策略，而vt可作为VG的近似值。

对局迭代的终止准则有两个：

1) 给定迭代次数t；

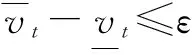
4 空战仿真实例研究

假设以敌我双方3对2无人机空战为例，即我方有2架无人机(U1,U2)，速度均为vi=225 m/s，空对空效能指数0.80。敌方有3架无人机(N1,N2,N3)，速度均为vj=200 m/s，空对空效能指数0.75。敌我双方雷达最大跟踪距离均为Rr=70 km，导弹最大射程均为Rmax=60 km，导弹最小射程均为Rmin=1 km，取k1=0.39，k2=0.15，k3=0.26，k4=0.2，l1=0.6，l2=0.4。假设敌我双方无人机每次攻击时只能攻击一个目标。敌我双方无人机空战态势由表1给出，双方无人机空战策略集由表2给出，表中φi j，qi j,ri j含义见1.1节。

表1 空战双方态势信息表Table 1 Situation information of both sides of air combat

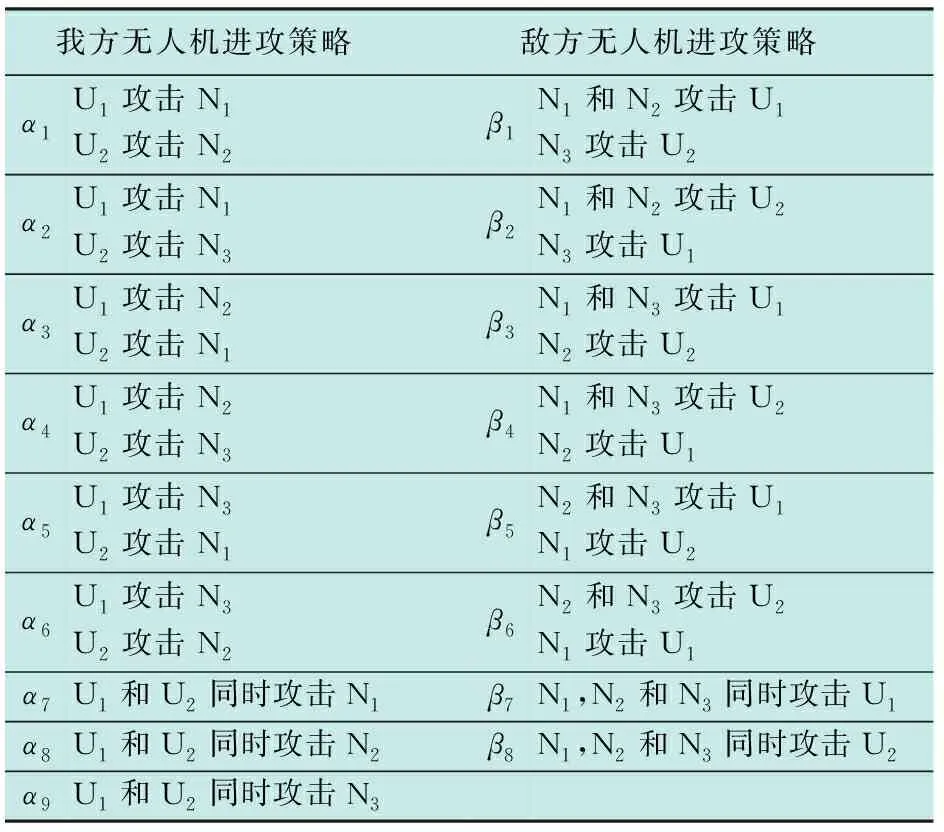
表2 敌我双方无人机空战策略集Table 2 The strategy set of air combat

由式(1)～(12)以及敌我双方空战参数，可以求出敌我双方无人机空战博弈支付矩阵A=

博弈支付矩阵A中每行的元素表示我方无人机的作战策略，每列元素表示敌方无人机的作战策略。其中，(αi,βj)表示我方无人机采取αi策略、敌方无人机采取βj策略时我方无人机获得的收益。

通过对局迭代对此种情况下的空战博弈纳什均衡值进行求解，在Matlab平台上进行仿真验证。

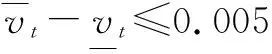
图3 允许误差Fig.3 Allowable error

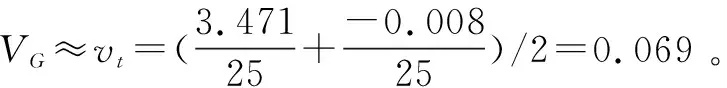
在敌我双方无人机25局博弈中，我方无人机选取1次策略α3，剩下24次都选取策略α2，敌方无人机选取1次策略β3和1次策略β7，剩下23次都选取策略β1。根据式(29)～(30)可知，我方无人机的近似最优策略x25为(0,24/25,1/25,0,0,0,0,0,0) ，同理可知，敌方无人机的近似最优策略y25为(23/25,0,1/25,0,0,0,0,1/25,0)，可以认为混合策略博弈Q*的纳什均衡解(x*,y*)近似等于上述(x25,y25)。即我方无人机以24/25的概率选取策略α2，以1/25的概率选取策略α3；敌方无人机以23/25的概率选取策略β1，以1/25的概率选取策略β3，以1/25的概率选取策略β7时可以得到纳什均衡。

从仿真结果可以看出，利用对局迭代能够得到敌我双方无人机空战的混合策略纳什均衡值，敌我双方可以达到一种平衡状态，如果任何一方破坏这种平衡状态都会使自己的收益减小。这样，敌我双方在考虑对方选取最优策略时能够找到一种对己方最有利的作战策略，从而实现无人机空战博弈，符合实际空战的情形。

对局迭代法与遗传算法对比见表3。

表3 对局迭代法与遗传算法对比Table 3 Comparison between game iteration method and genetic algorithm

由表3可以看出，求解相同情况下的空战博弈纳什均衡时，对局迭代法相对于遗传算法收敛更快，并且没有陷入局部最优值的风险。

5 结论

本文针对多无人机空战博弈问题进行了研究。根据敌我双方空战态势和效能参数信息建立敌我双方无人机空战博弈模型，给出了混合策略纳什均衡的推导步骤，利用对局迭代在Matlab平台进行仿真求解出了博弈的纳什均衡值，完成在双方博弈时考虑敌方策略的同时选取最有利己方的策略，符合空战情形，并且与遗传算法等方法相比，此种方法不存在陷入局部最优值等问题，是一种在空战博弈中求解纳什均衡值较为科学的方法。