基于改进阻塞矩阵的抗主瓣干扰算法

潘鑫锐， 宫 健， 陈 赓， 郭 乾

(空军工程大学，西安 710000)

0 引言

随着电子对抗领域的不断发展，雷达信号所处环境日益复杂，干扰样式日益多样，相对应信号处理的手段越来越多，对应抗干扰的技术手段也逐渐增多[1-3]，在阵列抗干扰处理中，自适应波束形成技术因能自适应提升雷达在未知环境中的抗干扰性能而得到重视与普及。当干扰从副瓣进入时，常规自适应波束形成技术能在干扰方向形成零陷,以此达到抑制干扰的效果[4]；当干扰从主瓣进入时，采用自适应波束形成技术会在主瓣内形成零陷，造成主波束畸变，并伴随有波束偏移、副瓣电平升高的问题，严重影响雷达的工作性能。针对此问题，有专家学者构建了阻塞矩阵进行预处理。

阻塞矩阵最早被提出来用于解决波束形成时协方差矩阵估计期望信号混入问题[5]，文献[6-7]最早提出运用阻塞矩阵对抗主瓣干扰,阻塞矩阵抗主瓣干扰算法通过构建阻塞矩阵，对接收信号进行预处理达到抑制主瓣干扰的目的。高阳等[8]对阻塞矩阵的性能进行了理论推导并进行仿真；沈伟等[9]采用Household变换构建出阻塞矩阵，解决了阻塞矩阵处理中白噪声被污染的问题；张萌等[10]将阻塞矩阵预处理与特征投影预处理相结合，新算法具有对快拍数敏感度低的优点，提高了算法的抗干扰效果。从已有文献中发现，在运用阻塞矩阵进行主瓣抗干扰的过程中，传统阻塞矩阵预处理会使期望信号的复包络发生变化，造成期望信号损失较大，不利于后续信号处理流程，现在少有研究相关解决办法，本文针对此提出一种改进的阻塞矩阵构造方式，用改进阻塞矩阵对信号进行预处理，仿真结果显示，改进的阻塞矩阵能在减少信号损失的同时，提高算法的抗干扰性能。

1 阵列信号模型

考虑对象为一个均匀线性天线阵列，阵元数为M，阵元间距d=λ/2，λ为波长，阵列天线结构如图1所示。

图1 阵列信号模型Fig.1 Array signal model

设定期望信号的入射方向为θ0，存在P个干扰源，对应产生干扰的来波方向为θi(i=1,2,…,P)， 阵列的接收信号为

X(t)=AS(t)+N(t)

(1)

式中：X(t)=[x1(t)x2(t)…xM(t)]T,表示阵列M个阵元在t时刻接收的信号；A=[a(θ0)a(θ1)…a(θn)],表示阵列流行矩阵，a(θi)=[1e-j2πd(sin θi)/λ…e-j2π(M-1)d(sin θi)/λ]T,表示第i个信号源的导向矢量；S(t)=[s0(t)s1(t)…sp(t)],为入射信号矢量;N(t)为t时刻各阵元接收的噪声矢量，设定各阵元接收噪声均为高斯白噪声，且独立不相关。

在后续对接收信号进行自适应波束形成时，根据线性约束最小方差准则(LCMV),对应自适应波束形成最优权矢量为

(2)

式中：a(θ0)为期望信号的导向矢量；Ri+n为干扰噪声的协方差矩阵。在实际运算中，干扰噪声协方差矩阵难以计算，常采用有限快拍数的采样协方差矩阵RX代替，即

(3)

式中：K为快拍数；RS为期望信号的协方差矩阵。

2 传统阻塞矩阵抗主瓣干扰方法

阻塞干扰矩阵的思路是通过构建干扰阻塞矩阵B对接收信号进行预处理，对主瓣干扰信号进行抑制，设定处理后的信号为Z，即

Z=BX

(4)

对于阻塞矩阵B，当存在一个主瓣干扰时，其构造为

(5)

式中，u1=2πd(sinθ1)/λ,θ1为干扰的方位角。

以第m个阵元为例，按照模型，第m个阵元在阻塞矩阵预处理前的数据为

(6)

式中，ui=2πd(sinθi)/λ,θi为第i个信号源的入射方向，对应经过阻塞矩阵预处理后，第m个阵元的输出数据为

(7)

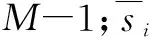
通过对比式(7)发现，经过阻塞矩阵预处理，当信号入射角度θi为主瓣干扰方向θ1时，对应接收到的主瓣干扰信号的复包络会置零，达到去掉主瓣干扰的效果，而对于阵列接收其他方向的信号，不会影响其角度信息，只改变接收信号的复包络的大小。

后续对预处理后信号进行自适应波束形成，最终抗干扰结果为

(8)

3 改进的阻塞矩阵抗主瓣干扰方法

根据上一节的分析，在阻塞矩阵预处理过程中，信号的复包络会发生变化，对期望信号产生一定的损失，不利于后续目标检测。针对此问题，本文提出了一种新的阻塞矩阵构造方法，与传统的阻塞矩阵相比，可以减少信号损失。具体结构为

(9)

经过新的阻塞矩阵预处理之后，对应预处理后信号矩阵Z′=B′X，此时M应为偶数，按照模型第m个阵元的数据为

(10)

通过对比可知，经过改进的阻塞矩阵预处理后，仍不改变信号的波达方向，对于主瓣干扰，其对应复包络仍为零,起到抑制主瓣干扰的作用，只改变接收信号的复包络的大小，即改变信号增益，相较于传统阻塞矩阵B，减少了信号增益损失。

同时，经过阻塞矩阵预处理后，进行自适应波束形成时自适应权偏离静态导向矢量[6]，使主波束发生偏移，针对该种偏移，采用权矢量补偿的方式进行解决，其实质是对导向矢量进行变换，过程为

aq=(B′B′H)a(θ0)

(11)

此时协方差矩阵变为

(12)

对应自适应波束形成的权矢量变为

(13)

最终抗干扰结果为

(14)

同时有

(15)

式中：Ys,BM表示接收信号中期望信号在抗干扰处理后的部分；Yi+n,BM表示接收信号中干扰和噪声在抗干扰处理后的部分。

综上，基于改进阻塞矩阵的抗主瓣干扰算法流程如下：

1) 根据干扰方向的先验信息，由式(9)构造出改进阻塞矩阵B′；

2) 依据Z′=B′X对接收信号X进行预处理得到Z′；

3) 依据式(11)对导向矢量进行更新；

4) 依据式(3)和式(12)计算预处理后接收信号的协方差矩阵；

5) 依据式(13)计算自适应波束形成权矢量wBM；

6) 计算得到抗干扰后接收信号YBM。

此过程中，抗干扰处理过后，记阵列输出的SINR为SBM，即

(16)

为具体分析改进阻塞矩阵的抗干扰性能，引入抗干扰信干噪比增益的性能指标[11]进行衡量，其定义为阵列输出的SINR与单个阵元上的输入SINR的比值，表示为

(17)

(18)

4 仿真实验

设定仿真条件为一个20阵元的均匀线阵，阵元间距d=λ/2；空间信号存在一个期望信号和一个互不相干的主瓣干扰信号；各通道间噪声是均值为0、方差为1的高斯白噪声；期望信号为线性调频(LFM)信号，方位角为0°，调频带宽为30 MHz，调频时宽为10 μs，采样频率为100 MHz，信噪比为0 dB。设定干扰信号为噪声调频干扰，对应干扰源方位角为2°，干噪比为30 dB。

4.1 改进阻塞矩阵预处理后自适应波束形成图(仿真1)

为验证本文所提新阻塞干扰矩阵的正确性与有效性，与传统常规自适应波束方向图进行比较，仿真参数设置如上，仿真结果如图2所示。

图2 自适应波束形成方向图Fig.2 Adaptive beamforming pattern

从图2(a)中可以看出，在主瓣干扰环境下，方向图在干扰方向上形成零陷，主波束严重变形，同时主波束发生偏移，对比图2(b)可以看出，经过改进阻塞矩阵预处理后，再进行波束形成时成功抑制主瓣干扰，主波束未发生变形失真，同时主波束未发生偏移，证明了该方法的有效性。

4.2 改进阻塞矩阵预处理后接收信号结果对比(仿真2)

进一步观察改进阻塞矩阵处理效果，仿真参数同上，阵列接收到的未进行阻塞矩阵预处理的单通道信号如图3所示。

图3 未处理接收信号Fig.3 Unprocessed received signal

利用式(14)对接收信号进行新阻塞矩阵预处理，预处理结果及其脉压结果如图4所示。

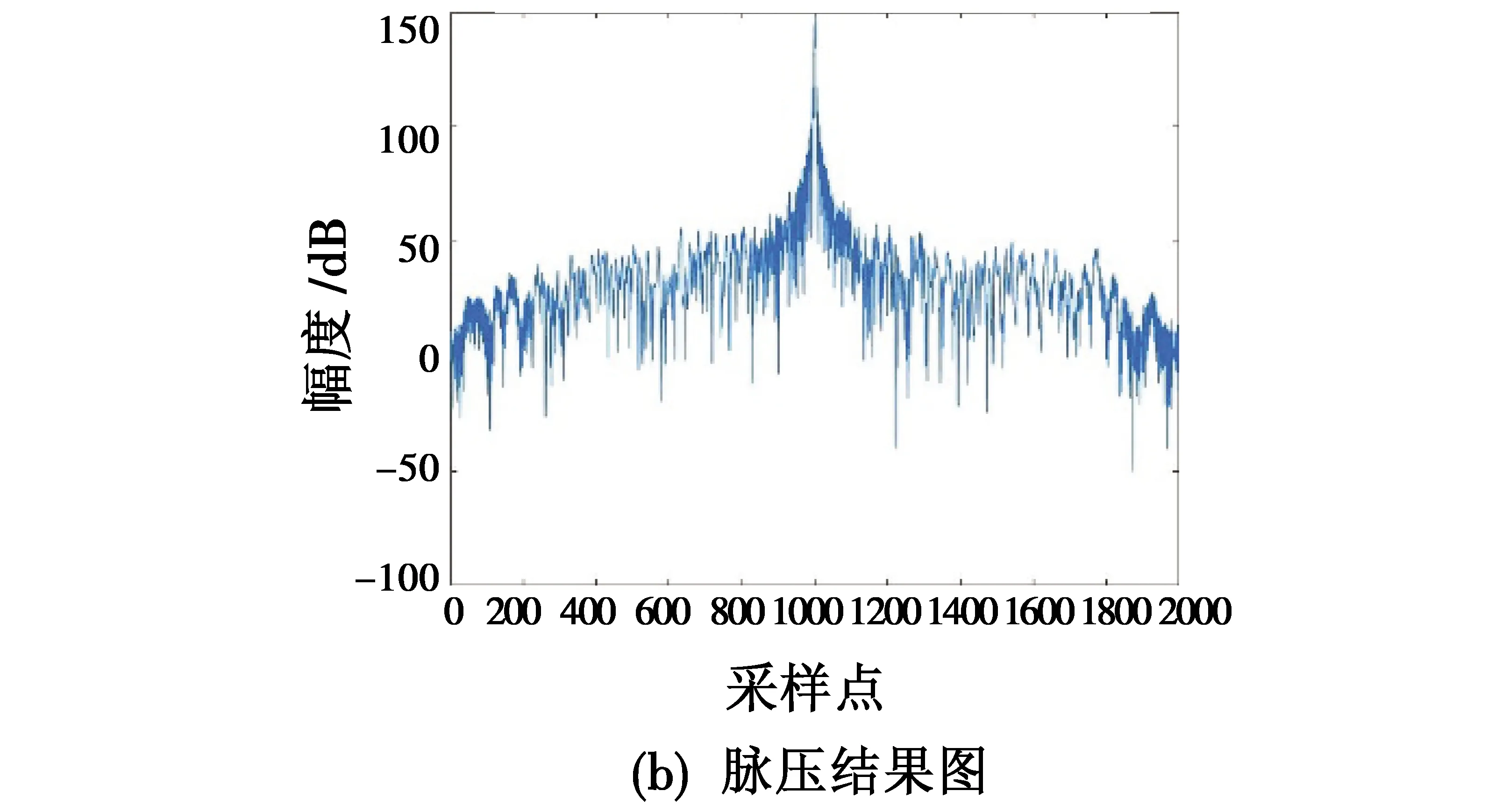
图4 改进阻塞矩阵抗干扰处理结果图Fig.4 Anti-interference processing result of the improved blocking matrix

从图4(a)中可以看出，阵列接收的总信号经过改进阻塞矩阵预处理后，接收信号的整体幅度大为减少，对干扰信号实现抑制，由第3章理论分析可知，在改进阻塞矩阵预处理的过程中，对主瓣干扰进行抑制的同时，期望信号也会有损失，处理后信号进一步进行脉压处理，结果如图4(b)所示，可以看出，经过脉压能清晰地看到目标信号，达到抗干扰目的，进一步证明了改进阻塞矩阵抗主瓣干扰方法的有效性。

4.3 信号增益随干扰入射角度变化曲线(仿真3)

为说明本文算法在改善信号损失方面的效果，与传统阻塞矩阵进行比较，设定期望信号θ0=0°保持不变，设定信噪比(SNR)为10 dB，干噪比(INR)为30 dB，其余参数同上，设定干扰方向从-10°～10°变化，处理后信号增益变化曲线如图5所示。

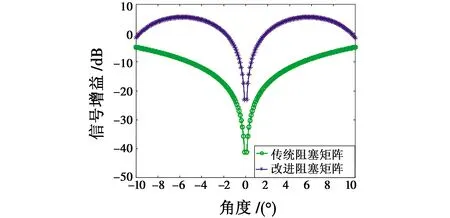
图5 信号增益随干扰入射角度变化图Fig.5 Change of signal gain with interference incident angle

从图5可以看出，在进行阻塞矩阵处理后，主瓣干扰的角度越接近期望信号，期望信号损失就越大。在相同条件下，对抗一个主瓣干扰时，本文提出的改进阻塞矩阵信号增益更高，对应期望信号的损失要小很多，证明了本文所提算法对于信号损失的改善效果。

4.4 抗干扰输出SINR增益随干扰入射角度变化曲线(仿真4)

为说明改进的阻塞矩阵预处理抗干扰过程中的抗干扰性能，以阵列输出SINR增益为标准，与传统阻塞矩阵的阵列SINR输出对比。设定期望信号θ0=0°保持不变，设定SNR为10 dB，INR为30 dB，此时对应Sin为-20 dB，其余参数同上，考虑主瓣干扰情况设定干扰方向从-10°～10°变化，依据式(17)，计算传统阻塞矩阵预处理与改进阻塞矩阵预处理抗干扰输出SINR增益，进行100次蒙特卡罗实验取均值，阵列输出SINR增益随干扰角度变化曲线如图6所示。

图6 输出SINR增益随干扰角度变化图Fig.6 Output SINR gain versus interference angle

从图6可以看出，当干扰从主瓣方向进入时，输出信干噪比增益降低，越靠近期望目标阵列输出SINR下降越严重，当干扰方向与期望目标信号方向一致时，信号也会因阻塞矩阵预处理而受到严重损失，从图中也可以看出，此时阵列输出SINR增益急剧降低，与理论分析一致。同时，从图6还可以看出，与传统的阻塞矩阵相比，本文提出的改进阻塞矩阵在同样的条件下，在单个阵元输入信干噪比为-20 dB的条件下，比传统阻塞矩阵预处理输出平均高出4 dB，证明了本文所提算法相较于传统阻塞矩阵抗主瓣干扰算法的抗干扰性能更佳，体现出本文算法的优越性。

4.5 抗干扰输出SINR增益随输入信噪比变化曲线(仿真5)

为进一步探究改进阻塞矩阵的抗干扰效果与输入信噪比的关系，设定干噪比为30 dB，设定信噪比范围为10～30 dB，其余条件同上，同时，与传统阻塞矩阵进行比较，进行100次蒙特卡罗实验，变化曲线如7所示。

图7 输出SINR增益随输入信噪比变化图Fig.7 Graph of output SINR gain versus input SNR

从图7可以看出，在干噪比不变的情况下，随着输入信噪比的增大，阵列输出SINR增益随之降低，理论分析是此过程中Sin增大所致，也说明阻塞矩阵预处理抗干扰算法在信号强度与干扰相差较大时性能更佳，更适合处理强干扰。同时，在整体信噪比增大过程中，本文所提算法处理后的阵列输出SINR增益总是比传统阻塞矩阵处理算法要高，说明了本文改进算法的抗干扰效果更佳。

5 结束语

本文从改善阻塞矩阵预处理过程中的信号损失为出发点，在传统阻塞矩阵抗主瓣干扰方法的基础上，提出一种改进的阻塞矩阵构造方法，进而提出基于改进阻塞矩阵的抗主瓣干扰算法，仿真结果表明，在相同条件下，改进的阻塞矩阵在主瓣范围内信号损失要少于传统阻塞矩阵，同时具有更佳的抗干扰效果。