基于改进Theta*算法的直升机三维航路规划
任天祥, 贺建良, 邹 杰
(中国航空工业集团公司洛阳电光设备研究所,河南 洛阳 471000)
0 引言
直升机在执行作战任务前需要规划好飞行路径,在低空飞行条件下考虑敌方威胁和地形回避等问题,规划一条从当前位置抵达目标位置的飞行航路,以提高直升机的生存概率和作战效率。航路规划是一个在复杂多约束条件下实现规划的过程,在遗传算法[1]、粒子群算法[2]、人工势场法[3]、传统A*算法[4]等多种智能算法和相关改进算法中,传统A*算法在三维航路规划问题上实现了良好应用。
Theta*算法[5]在路径搜索过程中结合传统A*算法和基于可视图A*算法[6]两者的优点,路径代价更小且减少了路径转向次数,航路更为平滑,但搜索速度相对变慢。本文在Basic Theta*算法的基础上采用变权重评估函数和减少无效节点计算量的方法改进了直升机三维空间航路规划算法,进一步减小规划航路的代价,提升搜索效率和路径规划效果。
1 威胁环境建模
直升机的三维空间全局航路规划问题可以转化为找到飞行经过的航路点集{s,x1,x2,…,xn,d},针对直升机低空飞行的特点,航路点以及航路点间的连线需要尽量避免规划空间中的威胁,包括地形威胁,主要是山峰和建筑物,还有局部涡流等恶劣气象威胁,雷达探测威胁,禁飞区威胁,其他威胁情况可以按照上述威胁模型简化。
1.1 地形威胁
地形威胁主要是对规划区域中的山体进行描述,单个山峰可以模拟表示为[7]
z(p,q)=hi*e-[(p-ai)/ki]2-[(q-bi)/ki]2
(1)
式中:(p,q)表示山峰表面某点在水平面的投影坐标;z为该点对应的高度值;hi为控制山峰高度的参数;(ai,bi)表示山峰中心的投影坐标;ki控制山峰的地形坡度。
图1为模拟山峰示意图。

图1 模拟山峰示意图Fig.1 Sketch map of simulated mountain
单座山峰对直升机的威胁值表示为
(2)
式中:Rm为直升机当前高度山体截面的最大半径;dm为直升机到该截面中心的距离。直升机与山体表面距离越近,危险越大;距离小于4 m表示直升机即将与山体相撞,威胁值为无穷大。考虑到直升机的飞行特性,设置直升机距离地形表面的最小高度为10 m,低于此高度直升机飞行过程有撞地风险。
1.2 恶劣气象威胁
恶劣气象威胁区域近似表示为圆柱体,对直升机的威胁值表示为
(3)
式中:de为直升机到圆形中心的距离;Re为该圆形的半径。恶劣气象威胁在直升机高度的水平截面是一个圆形,在威胁圆内,直升机距离圆心越近,危险越大。
1.3 雷达探测威胁
雷达探测威胁区域表示为球体,对直升机的威胁值表示为
(4)
式中:dr为直升机到威胁球心的距离;Rd为威胁球体的半径。
1.4 禁飞区威胁
直升机进行航路规划时需要避开规定的禁飞区域,飞行航线不能落入禁飞区中。禁飞区对第i段航路的威胁值可以表示为
(5)
式中:ri为第i段航路路径;ZNF为禁飞区空间,两个区域若有交点,则威胁值为无穷大。
2 改进的Theta*算法
2.1 Basic Theta*算法
A*算法是一种常用的启发式路径搜索算法,通过不断评估规划空间中搜索节点的代价来确定最优路径。Basic Theta*算法是A*算法的一种变体,与A*算法的估价函数均可表示为
f(n)=g(n)+h(n)
(6)
式中:g(n)表示从起始节点s到当前节点n的航路代价;h(n)表示从当前节点n到目标节点d的航路代价。A*算法中一个节点的父节点一定与该节点相邻,而Basic Theta*算法没有此限制。记节点n的父节点为p(n),与节点n相邻的节点集合为N(n),节点n′属于N(n)。Basic Theta*算法判断p(n)和每个节点n′之间是否可视(即是否存在障碍物),并据此选择代价更小的路径。Basic Theta*算法的搜索流程如下。
1) 初始化open表和close表,将起始节点s插入到open表中。
2) 若open表为空,搜索失败,退出程序。
3) 从open表中取出路径代价f(n)最小的节点插入到close表中作为当前节点n。
4) 若当前节点n是目标节点d,则通过节点n的父节点p(n)回溯到起点,即找到路径节点集合,算法搜索过程结束;若节点n不是目标节点d,则执行5)。
5) 对节点n的相邻节点集合N(n)中的每个节点n′执行如下操作:若节点n′在close表中,则忽略节点n′;否则执行6)。
6) 计算节点n′的代价并检查节点p(n)与节点n′的可视性。
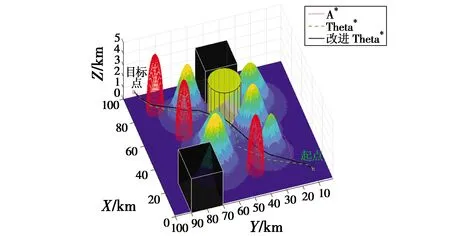
① 若p(n)和n′两节点之间可视,那么飞行航路s→…→p(n)→n→n′的路径代价记为g(n′),飞行航路s→…→p(n)→n′的路径代价记为g(p(n))+c(p(n),n′),其中,c(p(n),n′)表示p(n)→n′的路径代价。若g(p(n))+c(p(n),n′) ② 若p(n)和n′两节点之间不可视,并且航路s→…→n→n′的路径代价g(n)+c(n,n′)小于航路s→…→n的路径代价g(n′),那么更新g(n′)=g(n)+c(n,n′),p(n′)=n。若n′此前已在open表中则更新n′,否则将n′ 插入到open表中。 7) 根据代价值对open表中节点排序,然后转到2)。 2.2.1 变权重航路代价评估函数 Basic Theta*算法的航路代价评估函数完全继承了A*算法,选择变权重的评估方法改进Theta*算法搜索效果[7],即 f(n)=αg(n)+βh(n) (7) 式中,g(n)和h(n)的定义决定了在航路规划的不同阶段,它们对路径搜索的影响效果不同。若β较大,算法运行初期搜索效果较好;若α较大,算法运行后期搜索效果较好。调整g(n)和h(n)的权重 α(x)=αmin+(αmax-αmin)(1-h(n)/D) (8) β=1-α (9) 式中,D表示起始节点到目标节点的欧氏距离。算法搜索过程中,α从最小值αmin变化到最大值αmax,提高了路径搜索的合理性。 直升机执行作战任务时,既要保证自身能够避开执行任务区域的威胁,又要保证飞行航路尽可能短,以缩短飞行时间、减少油耗。因此航路代价函数设计为 (10) 式中:Li为第i段航路的长度代价;Ti为地形威胁代价;Ei为恶劣天气威胁代价;Pi为雷达探测威胁代价;Zi为禁飞区威胁代价;ω1,ω2,ω3,ω4,ω5分别为对应威胁值的权重。Li的算式为 (11) 式中,(xi,yi,zi),(xi+1,yi+1,zi+1)分别是第i段航路起点与终点的横坐标、纵坐标和高度坐标。 设航路节点n的坐标为(xc,yc,zc),目标节点d的坐标为(xd,yd,zd),启发函数h(n)表示为 (12) 2.2.2 改进路径节点搜索过程 Basic Theta*算法搜索时间较长的主要原因是需要做大量的可视性检查。有多少点进入open表就要执行多少次节点可视性检查,若规划空间的栅格数量较多,则用于判断可视性的计算量较大,进而影响路径节点搜索速度。 实际航路规划情况中,有很多进入open表的集合N(n)中的节点n′最终不属于路径节点,这意味着有大量可视性检查是无效的,因此,从减少检查次数这一方面来改进节点搜索过程。 改进算法假定节点n的父节点p(n)与相邻节点集合N(n)中的所有节点n′都具备可视性,即对所有节点n′执行Basic Theta*算法步骤6)中的①操作。改进算法将节点可视性检查放在原来的步骤3)和4)之间,如果两点可视,算法继续执行;否则,重新计算n′及其父节点。改进算法中只有真正要扩展的节点才会实际执行可视性检查,显著减少了运算量。 基于Matlab R2017A软件平台进行算法仿真。设置直升机的起始节点坐标为(10,10,0.1),目标节点坐标为(95,95,1),单位均为km。规划区域的山峰、恶劣天气区域、禁飞区以及雷达参数分别如表1-表4所示。 表1 山峰地形参数Table 1 Parameters of the mountains 表2 恶劣天气区域参数Table 2 Parameters of the bad-weather area 表3 禁飞区参数Table 3 Parameters of the no-fly zones 表4 雷达参数Table 4 Parameters of the radars 图2为三维航路规划路线图。 图2 三维航路规划路线图Fig.2 Schematic of 3D path planning results 分别使用A*算法、Theta*算法和改进Theta*算法在相同三维规划空间中进行航路规划。A*算法和Theta*算法的路径代价权重均取α=0.4,β=0.6;改进Theta*算法的路径代价权重取αmin=0.4,αmax=0.6。 图3为二维平面航线示意图。 图3 二维平面航线示意图Fig.3 Schematic of the 2D planned paths 从图2和图3可以看出,本文提出的改进Theta*算法与其他算法相比,规划航迹更加平滑,能够有效对任务区域中的各种威胁进行回避。 各算法规划出的航迹参数见表5。 表5 航迹参数表Table 5 Parameters of the paths obtained 通过对比表5中数据可以发现,对航路代价函数权重α和β的实时调整,有效地降低了航路规划代价,缩短了规划时间。 本文在Theta*算法基础上采用实时调整航路代价估计权重的航路评价函数,并通过改进航路搜索过程来减少可视性检查计算量,提升了规划效率和规划效果。通过对直升机低空飞行过程中存在的威胁进行分析建模,分别用A*算法、Theta*算法和改进Theta*算法进行航路规划。仿真结果验证了本文的改进Theta*算法可以有效缩短规划时间、减少规划步数、减小航路规划代价,是一种有效的三维路径规划算法。2.2 改进的Basic Theta*算法
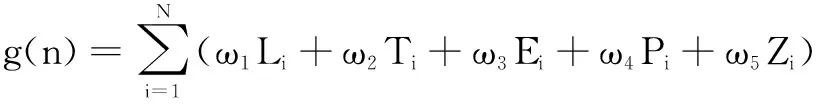
3 仿真结果与分析
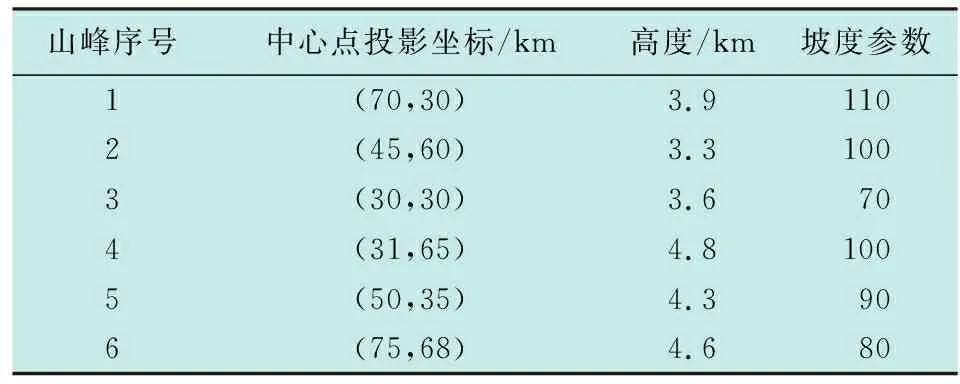
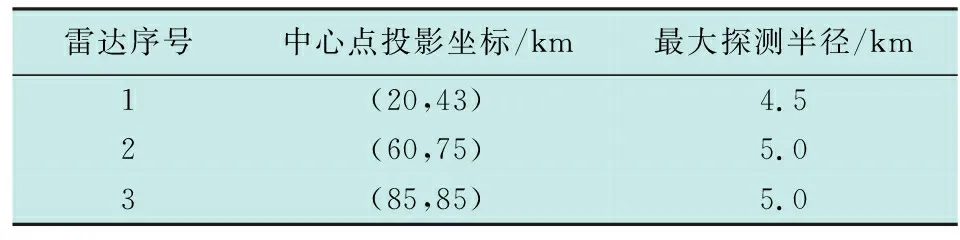
3.1 航路规划空间定义


3.2 航路规划结果和分析
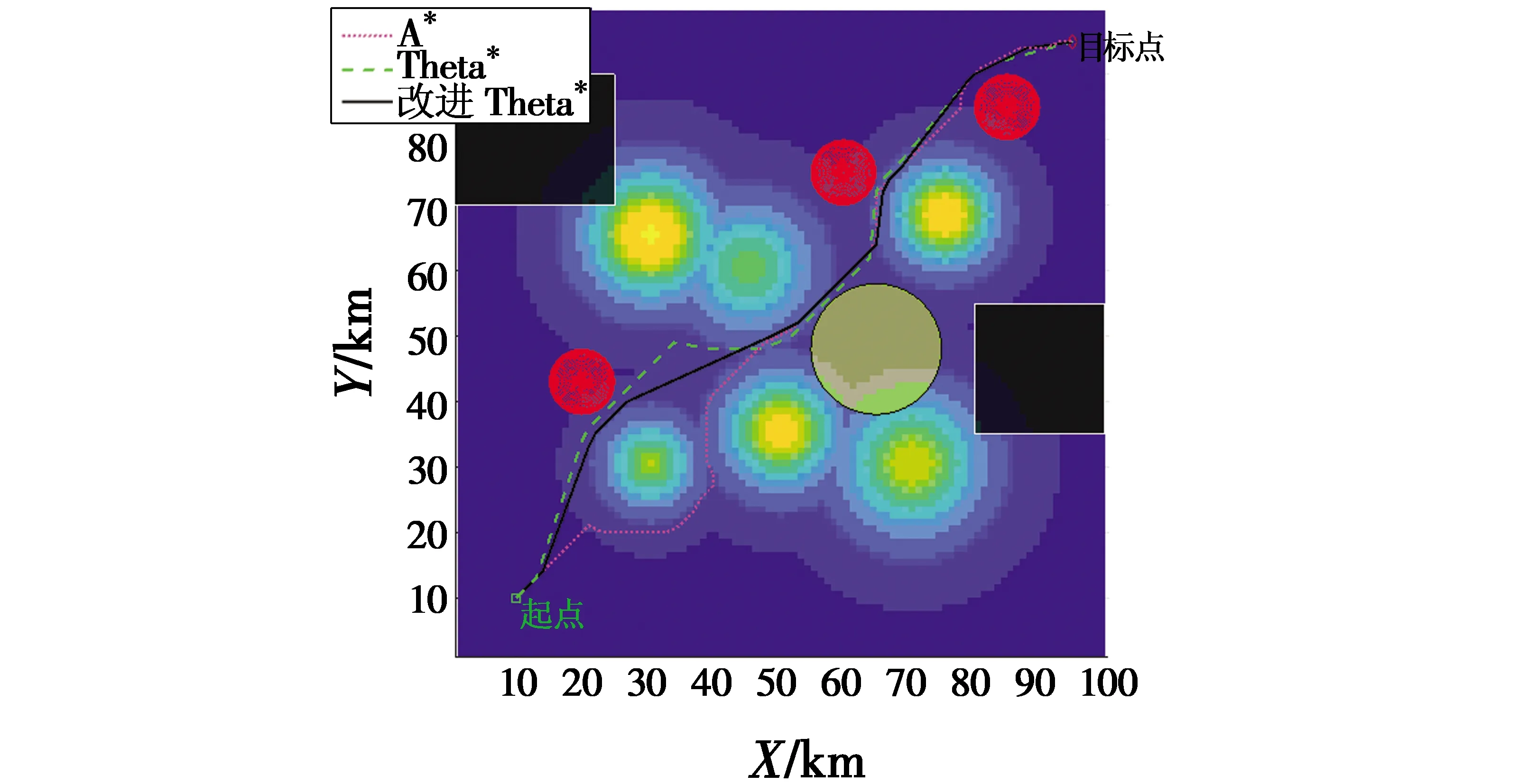
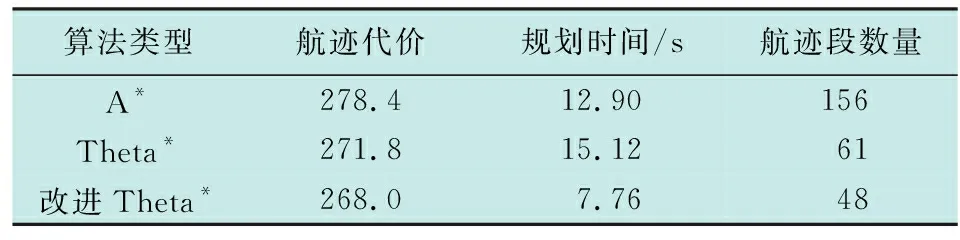
4 结束语

