逆混合变分不等式的弱尖锐性
黄 辉,顿欣欣
(云南大学 数学与统计学院,云南 昆明 650091)
广义逆混合变分不等式(GIMVI)叙述如下:
设X是实Banach 空间,Ω 是X中的非空闭凸集,φ:X→X∗是映射,f:X∗→R 是函数.寻找x∗∈Ω,使得
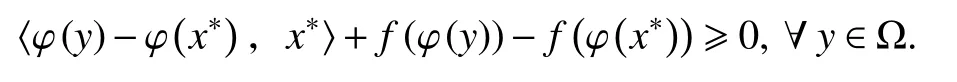
弱尖锐性在数学规划的灵敏度分析和算法的收敛分析有着非常重要的应用.Chen 等[1]研究了逆变分不等式的Tikhonov 正则化方法.Al-homidan 等[2]利用Ekeland 变分原理的均衡形式给出了弱尖锐性的特征.Nguyen 等[3]推广了最优化问题的弱尖锐值概念和变分不等式问题的弱尖锐解概念,并给出了弱尖锐性存在的充分条件.Marcotte 等[4]介绍了变分不等式的弱尖锐性,引入了仿单调的概念,证明了解集具有弱尖锐性当且仅当变分不等式对偶间隙泛函有误差界;在函数连续且仿单调的假设下,给出了对偶间隙函数的几个性质.文献[5]研究了Hilbert 空间中变分不等式的弱尖锐性,得到了几个等价条件.Hu 等在文献[6]中,提出了自反、严格凸且光滑的Banach 空间中,变分不等式问题的解具有弱尖锐性的概念,给出了几个等价条件,同时还证明了在一定的条件下,可以通过求解有限个具有线性目标的凸优化子问题来获得变分不等式问题的解.Wu[7]研究了具有伪单调映射的变分不等式,在不使用间隙函数的情况下刻画了解集的弱尖锐性.文献[8]利用原间隙函数研究了变分不等式解集的弱尖锐性,并且给出了求解变分不等式问题的算法的有限收敛性.文献[9]研究了Banach 空间中混合变分不等式原间隙函数与弱尖锐性的关系,同时给出了弱尖锐性存在的充分和必要条件.文献[10]考虑了与弱尖锐性密切相关的集值映射的度量次正则性.
本文在文献[9]的基础上研究了Banach 空间中广义逆混合变分不等式(GIMVI)解的存在性.在 φ 是线性连续映射且在 Ω 上单调、f连续且是凸函数的条件下,从高阶弱尖锐性得到了原间隙函数的高阶误差界,并给出了解集具有1 阶弱尖锐性的2 个充分条件和必要条件.与文献[9]相比,有2 方面的不同:一 是考虑的模型不同,文献[9]考虑的是混合变分不等式;二是文献[9]只考虑了1 阶弱尖锐性.
1 预备知识
我们使用如下假设:设X和Y都是实Banach 空间,X*是X的拓扑对偶空间,Ω ⊆X是非空子集,用cl(Ω),c o(Ω),b dry(Ω)分别表示闭包、凸包和边界,分别是X和X∗中的闭单位球,SX∗ 是X∗的单位球面.
定义 1[11]设g:X→R∪{+∞}.如果定义域

2 主要结果
考虑(GIMVI)的弱尖锐性时,需要假定(GIMVI)的解集非空.下面给出(GIMVI)存在解的1 个充分条件.
定理 1在(GIMVI)中,设 Ω 是弱紧凸集,φ 是弱连续映射,f是连续映射,fφ 是凸函数,且对每一个z∈Ω,〈φ(·),z〉 是凸函数,则(GIMVI)至少存在一个解.
证明 定义集值映射G:Ω →2X为

显然y∈G(y),因此G(y)不是空集.又因为 φ 是弱连续映射,f是连续映射,所以G(y)是弱闭集.
下面我们利用反证法证明G是KKM 映射.假设存在有限集 {z1,z2,···,zk}⊆Ω 和z∈co{z1,z2,···,zk} 使得z∉G(zi)(i=1,2,···,k),则

推论1 在(GIMVI)中,设G是紧凸集,φ 是连续线性映射,f是连续凸函数.则(GIMVI)至少存在一个解.





3 总结
本文研究Banach 空间中逆混合不等式的弱尖锐性,基于对偶理论,得到了弱尖锐性存在的2 个充分和必要条件.下一步拟研究向量变分不等式的弱尖锐性.

