一类酉约束矩阵迹函数最大值问题的解析解

余俊伟，陆明杰，徐玮玮

(南京信息工程大学 数学与统计学院，江苏 南京 210044)

矩阵优化问题在数据科学、控制理论、电子结构计算和特征值计算等问题中有着非常重要的应用[1-12].本文我们将考虑如下的矩阵优化问题：

其中 Γk，∆k，Hk分别是m×n，n×t，t×m复对角矩阵，k=1,2;c是复数，tr(·)表示矩阵迹函数，Im是m×m单位矩阵.

这类酉约束矩阵迹函数最大值问题有着比较重要的理论和应用意义.比如对于信号重构，我们在重构空间中会获得不同方向上具有不同频带能量的信号.现有方法基于奇异值进行相空间重构，得到反映突变信息的信号分量.由于信号比较复杂，不利于提取局部突变信息，可以利用奇异值特征完成对信号的重构，同时将其与背景信号分离来获得故障信号的一些信息.[13-14]

对于故障诊断，假设机械系统的测试信号是以下数值序列：xi,i=1,2,···,2n−1，同时令重构矩阵D为

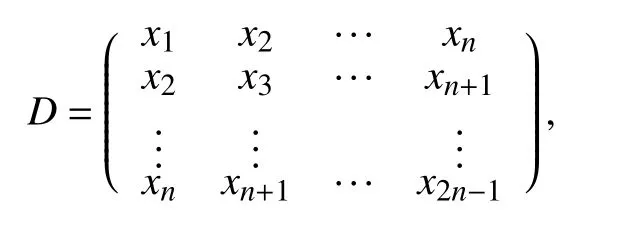
假设设备正常工作，我们用x(t)表示传感器的测试信号，其中包括已确定的信号s(t)，高斯白噪声n(t).则x(t)=s(t)+n(t),其中信号s(t)与噪声n(t)不相关.同时，测试信号x(t)的重构矩阵Dx是信号s(t)的重构矩阵Ds和噪声n(t)的重构矩阵Dx的叠加，即Dx=Ds+Dn.此外，假设在一段时间后，新的测试信号y(t)添加了一个新的故障信号，例如碰撞部件d(t),则有y(t)=s(t)+n(t)+d(t).新测试信号y(t)的对应重构矩阵为Dy为Dy=Ds+Dd+Dn,其中Dd为d(t)的重构矩阵，Dd=Dy−Dx[14-15].我们使用矩阵Dd的奇异值和来估计故障信号d(t)的能量，分别用N和表示样本数和阈值，其中f是故障前的信号时频窗函数，mi是频带.由此来重构矩阵：

可见振荡主要出现在尾端.在数据处理过程中，尾端点部分可以适当扩展，当数据处理完成后，扩展部分将被丢弃，碰撞摩擦信号的特征频率可以从重构的分解信号中再现.

假设B∈Cn×n是Hermitian 半正定矩阵，且

其中c是实数，Aj是n阶复矩阵，σi(Aj)表示Aj的奇异值并且 σ1(Aj)≥σ2(Aj)≥···≥σn(Aj)≥0 ，j=1,···,m.这 些问题可应用于基因表达水平分析，机械系统的信号测试与航空发动机故障诊断等领域[1].

1 准备知识

在本文中，令 C，N+，Un，R 和 Cm×n分别表示复数集、正整数集、n阶酉矩阵集、实数集、m×n复矩阵集.σi(A)代表矩阵A的第i个奇异值，tr(·)表示矩阵迹函数，Om×n表示m×n零矩阵，In表示n阶单位矩阵，设x为复数，|x| 表示x的模，Re(x)表示x的实部.

引理 1[1]如果A1,···,Am∈Cn×n，c∈R，σ1(Aj),···,σn(Aj)是Aj的奇异值，并且 σ1(Aj)≥σ2(Aj)≥ ···≥σn(Aj)≥0 ，j=1,···,m.则

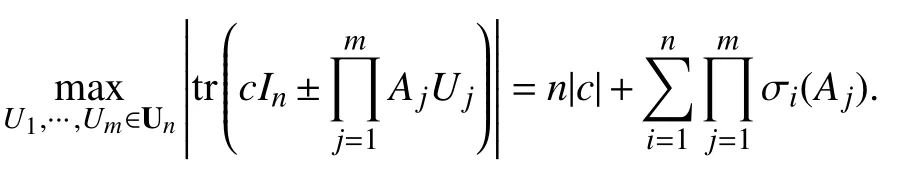
2 主要结论

在本节中，我们考虑(1)中的一类酉约束矩阵迹函数的最大值问题.

由（7），（8），（9）式可知定理1 得证.证毕.

注1 定理1 将(3)中Aj从同维复矩阵推广到不同维复矩阵，c从实数推广到复数.因此，定理1 改进了 引理1 的结果.

3 数值算例

本节我们将给出一个随机算例来验证定理1 的有效性.

算例 1结合前面应用背景(2)，令

其中B1=diag(2,7,14,23,44,21,62,79,98,7,3,167,194,8,254,287,6,359,112,221),使用随机酉矩阵U1和U2计算 | tr(20×I20+U1BU2A)| 得图1.

图1 对于不同随机酉矩阵 U1 和 U2 计算|tr(20×I20+Fig.1 Computing |tr(20×I20+U1BU2A)| for different random unitary materices U1 and U2

同时结合(2)可得

因此，数值算例1 的结论验证了定理1 的有效性.

4 总结

本文我们研究了一类酉约束矩阵迹函数最大值问题的解析解：