一种面向山区场景的多信道接入策略

彭 艺，谢钊萍，魏 翔，朱桢以

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

近几年来，随着无线通信技术的快速发展，农村、丘陵和山区环境中无线信号的使用也变得更加广泛[1-4].但在一些山区场景中，会出现信道占用极少的情况，容易造成频谱资源的浪费.为了能充分利用频谱资源，在认知无线电网络中主要通过有效的接入技术实现授权用户（Primary Users，PU）和次要用户（Secondary User，SU）的频谱共享.

到目前为止，研究人员已经提出了许多信道接入的方法.例如：Sara[5]提出了一种具有反馈的接入算法，该算法可以避免PU 与SU 之间发生碰撞，最大限度地提高SU 的服务速率；王若男等[6]针对多种数据需要发送的情况提出一种损失制接入算法,优化参数，有效减少频谱空洞；文献[7-8]提出自适应的接入模型，与非自适应的方法相比，具有较好的预测精度，且误报率更低；文献[9-12]提出应用深度学习的方法预测信道状态，得到的预测结果稳定且快速地预测出了信道值，是用于信道接入和信号检测有效的方法.以上这些算法使用的无线数据传输方式都是基于单信道的，极大地限制了数据传输速率.为此，文献[13]提出一种多信道通信策略，建立非合作博弈论模型，提高认知无线电网络的有效容量；文献[14]建立短波多用户信道选择策略，选出了所需的空闲信道数量，为认知用户提供了等效宽带传输；文献[15-18]考虑网络流量和用户行为，提出向多通道进行动态访问的算法.这些文献都表明多信道方法的可行性.本文将多信道与山区场景进行结合，向多个信道采用机会主义频谱访问，利用智能算法的优点，提出符合山区场景的多元隐马尔可夫信道接入算法.

1 系统模型

认知无线电是一种智能的无线通信系统，能够捕获或感知无线信道中的信息，从而得到某个时隙或某个空间中未使用的频谱资源.

认知无线电网络系统通常主要由两部分组成：PU 和SU.PU 具有使用频谱的优先权，当PU 不存在时，SU 可以利用频谱空洞获得某个频段的使用权.如图1 所示，存在m个授权用户P={p1,p2,···,pm} 和n个次要用户S={s1,s2,···,sn} 的多信道山区系统，其中山林环境中的树木和石块对信号传输会造成一定的衰落、衍射和吸收.

图1 多用户系统模型Fig.1 System model of multi-user

传统的频谱感知方式是一个时隙进行一次频谱感知，SU 在进行信道接入前，需要对每个时隙都进行频谱感知，如图2（a）所示.改进后的系统采用机会式频谱感知方式，每个授权信道可以划分为t个时隙，若第g（1 ≤g≤t）个时隙处于忙碌状态，则在第g+1 个时隙将不再进行感知，在g+2 个时隙才再次进行感知，判断信道状态；若第g（1 ≤g≤t）个时隙处于空闲状态，为了避免信道接入过程发生冲突，在g+1 时隙仍还需要对其进行感知，具体的频谱感知过程如图2（b）所示，绿色部分表示感知时间，这样可有效地减少频谱感测过程中所需的感知时间，提高认知用户的传输速率.

图2 频谱感知对比图Fig.2 Comparison graph of spectrum sensing

2 多信道接入策略

根据提出的频谱感知模型可以看出，缩短频谱感知时间可以加快数据传输速率，提高频谱资源的利用率，而多信道的接入策略既可以更好地描述真实的传播环境，又可以提高信道传输的可靠性.

因此，本文设计了一种多信道接入策略，如图3所示.在该策略中，将基站授权的总带宽均匀划分为k个带宽相同的信道，SU 用户对信道进行感知，每个信道具有信道忙碌和信道空闲两种状态，在感知到信道空闲时，SU 用户进行接入，若在当前信道的下一时隙信道状态为忙碌，也可对相邻的其它的信道进行感知，直到感知到的当前信道和相邻信道都无空闲时隙时，SU 用户进入等待状态.

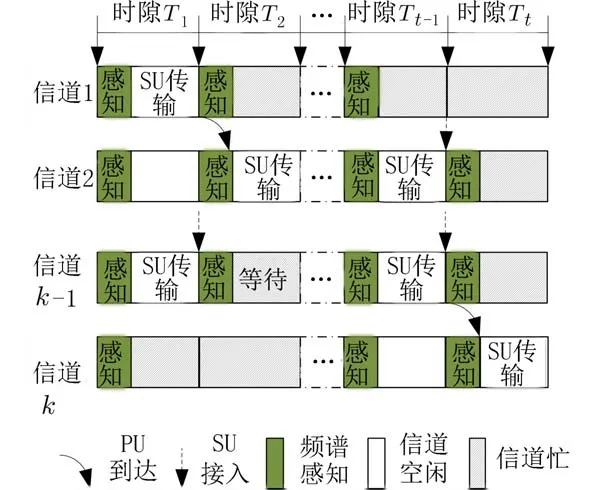
图3 多信道接入策略Fig.3 Strategy of multi-channel access

3 基于多元隐马尔可夫的接入算法

针对多元信道接入策略，本文提出的多元隐马尔可夫模型由两部分组成，如图4 所示.第一部分由信道的真实情况序列组成，第二部分由观测序列组成.

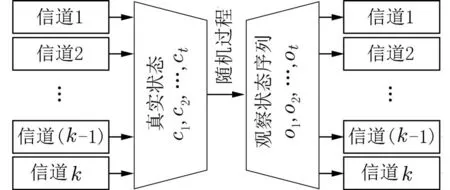
图4 多元隐马尔可夫结构图Fig.4 Structure graph of multiple hidden Markov

在t个时隙内，用cg表示每个时隙信道的真实状态，og表示状态相关的随机变量.简单来说，cg经过随机过程，到达观测部分og，og的分布仅取决于当前状态cg，而不取决于先前的状态与观测值，各信道之间条件独立性成立.

3.1 改进隐马尔可夫算法参数估计隐马尔可夫模型状态之间的变化由马尔可夫链的转移概率控制.转移概率和对应的观测概率可定义为：

假设我们观察到一系列观测值C={o1,...,ot}，通过最大似然估计可以得到相对应的概率为：

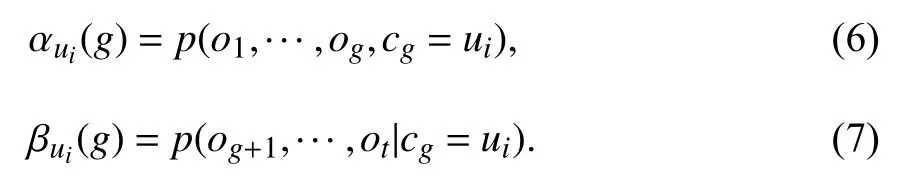
根据前向概率，可以将似然函数计算为：

将得到的函数表达式进行参数估计时采用期望最大化算法（Expectation Maximization，EM），未观察到的量视为缺失.

定义观测数据为：

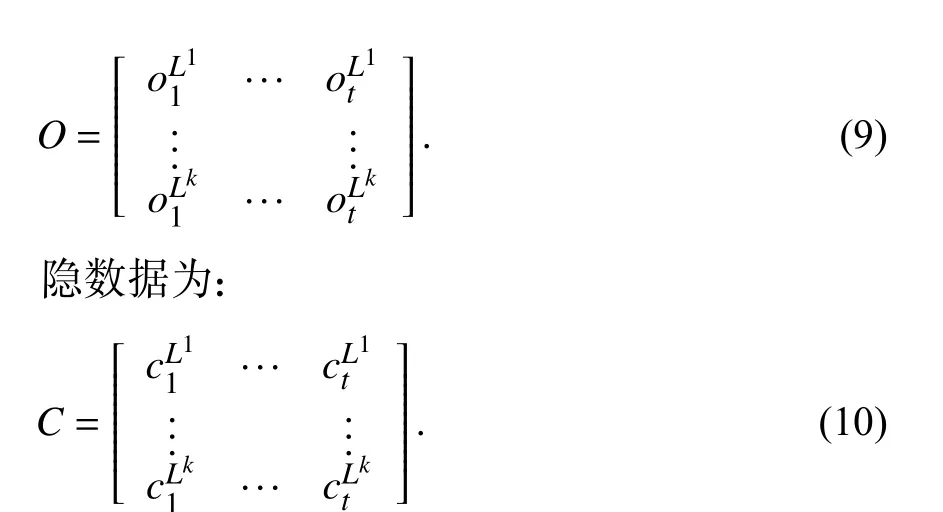
式中，O∈Rt×k，C∈Rt×k，(O,C)为完全数据，对数似然函数 l gP(O,C|Λ)；并定义缺失数据的随机变量是完整数据的可能性根据丢失的数据可写为：

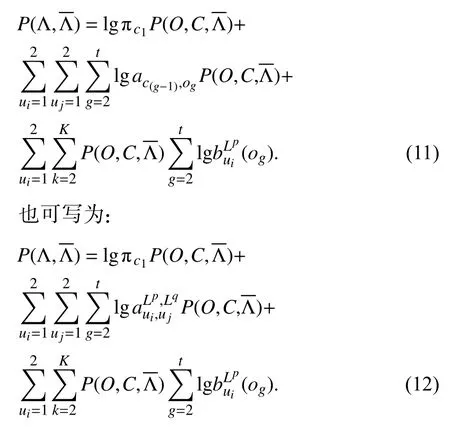
EM 算法的具体步骤如下：

步骤 1 使用观测到的数据和当前估计值计算后向概率和前向概率.

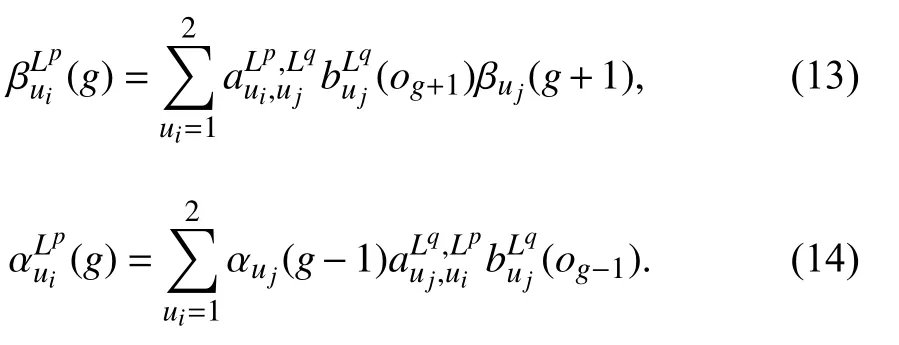
并利用前后向概率，计算当前变量的期望值.定义当前估计的概率

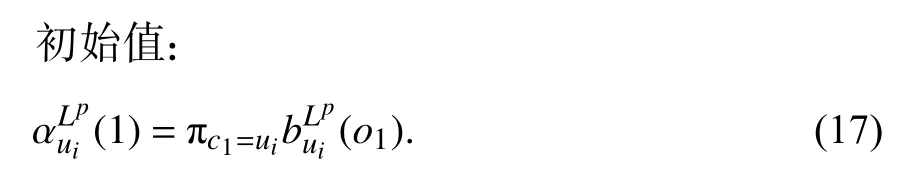
步骤 2更新参数估计值.

进行更新的过程默认为迭代的过程，如果指定了收敛准则，则停止迭代，否则返回步骤1 进行另一次迭代.

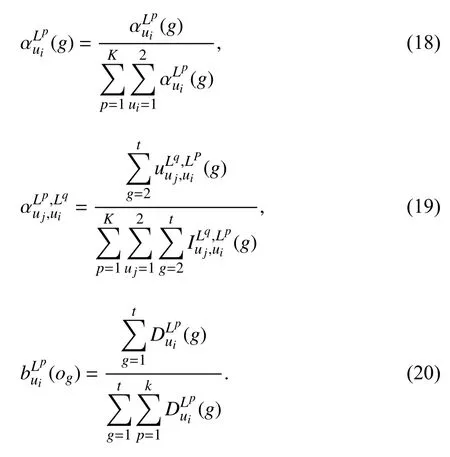
步骤2 等效于最大化离散模型的加权对数似然，如果可以使用良好的初始估计，则数值优化效果很好.另外，对于步骤2，由于使用了一个迭代过程，极大地减少了计算时间.

3.2 最优接入路径采用维特比算法，使用一种基于动态规划的方式寻找最佳状态序列，即把整个信道路径按照时隙分成每一个小序列，基于每一步的结果再去寻找下一时隙的策略，这样就可以通过寻找局部最优去寻找得到全局最优解.

首先，定义两个变量 δ 和 φ，δ 表示为时刻g状态为ui的所有信道中概率最大值，φ 表示为时刻g状态为uj，在g− 1 时刻状态为ui的概率最大值子信道.则可得到：

本文设计的改进式隐马尔可夫接入策略流程步骤如下：

步骤 1通过频谱感知获取信道状态信息；

步骤 2对接入模型进行理论分析，通过式（2）和（3）得到多元转移概率；

步骤 3进行参数估计，根据观测到的历史信道信息，预测出未来时隙的信道状态；

步骤 4进行参数更新，通过式（22）和（23）得到概率最大值子信道，建立候选信道路径；

步骤 5反复进行步骤3～4，优化参数，直至得到最优接入路径，则算法结束.

3.3 算法性能分析按照图3 的接入策略，PU 到达信道速率服从参数为 λp的泊松分布，占用单个信道时隙 ψ 由感知时隙 ϕ 和数据传输时隙 γ 两部分组成.当用户选择第p个信道进行接入时，如果感知第p个信道处于空闲状态，用户能够实现信道接入.此时收益为fLp=1，K个信道t个时隙的累积收益为 ：

由式（28）、（29），可以得到SU 和PU 发生碰撞的概率为：

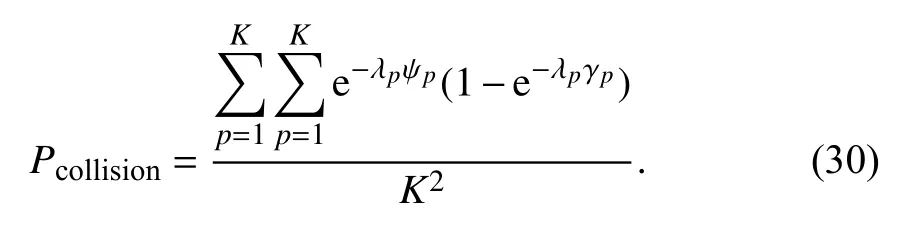
4 仿真实验及结果分析

4.1 构建测试环境本次测试，发射机频率为709 MHz，发射功率为43 dBm，站点位于昆明市某山顶部，该地区含有人工种植松树树木和少量石头，树木之间的相隔距离为4～6 m，信号在50 m 范围内时，树木表层仅存在反射现象.打开Global Mapper软件，导入测试场景的地图，在弹出的对话框中，任意选择某一坐标为发射点，得到传播路径如图5 中黄线所示.从图5 可以清晰看到场景具有一定的起伏性.

图5 测试场景3D 效果图Fig.5 3D rendering of the test scene

进一步，我们可以得到该条路径的地形剖面图如图6 所示.图6 横坐标反映出发射点与接收点之间水平传输距离为0.637 km，纵坐标垂直高度为45 m.有效且直观地反映出两点之间的地形起伏情况.

图6 地形起伏情况剖面图Fig.6 Cross-sectional view of terrain undulation

4.2 仿真结果分析本文基本仿真参数设置如下：SU 用户数S=20，信道具有相同传输速率1 Mb/s，将文献[13-14]提出的多信道接入策略与本文算法进行比较.图7 为不同信道数量的数据传输概率仿真图，由图7 可知，随着平均时隙增大，在实线处，信道数量K=2 时,3 种算法都具有较高的成功传输概率,当在虚线处信道数量K=8 时,本文算法成功传输概率能达到65%，这是由于算法不仅考虑了同信道之间的数据传输,还考虑了相邻信道的数据传输,因此具有较优的信道收益.

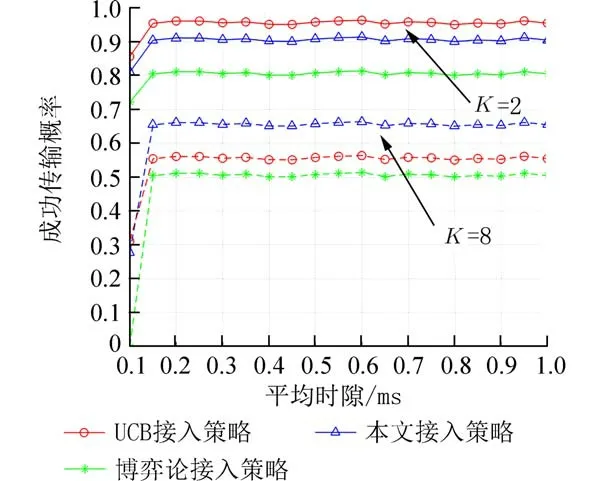
图7 不同信道数量的传输成功概率Fig.7 Transmission success probability under different channel numbers

接着，我们从PU 用户和SU 用户角度出发，考虑了3 种算法的碰撞概率.由图8 可见，当试图提高PU 用户的到达速率参数时，参数提高为3.0 时，本文算法碰撞概率达到24%，在多信道中具有较低的碰撞概率.在多信道中具有较低的碰撞概率，这是由于改进了频谱感知策略，使得信道碰撞概率优化效果明显.

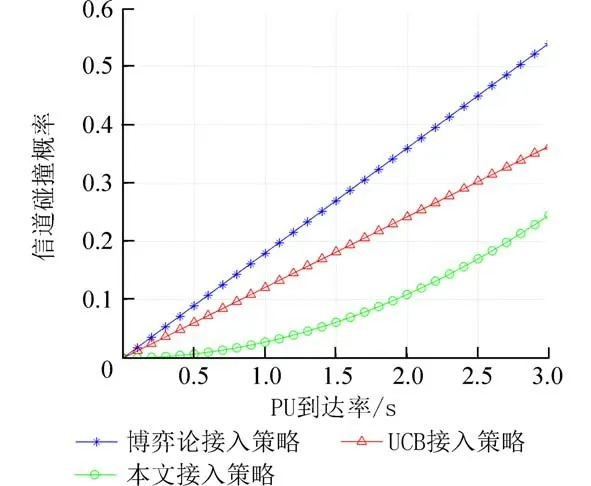
图8 信道碰撞概率对比图Fig.8 Comparison of channel collision probability

5 结束语

本文提出一种多信道的接入策略，考虑山区环境下的传播特点，对传统的隐马尔可夫算法进行改进，使其可容纳多个次级用户.通过仿真实验，证明新算法具有较稳定的接入性能，且信道效率得到明显提高.在信号弱覆盖场景下，具有明显的优势.新算法为山区场景提供一个具有理论指导意义的信道接入方案，在未来的工作将考虑对历史信道数据进行训练以提供一个可靠的数据源模型.