基于非支配排序遗传算法的细纱工艺参数优化
邵景峰, 石小敏
(西安工程大学 管理学院, 陕西 西安 710048)
在第七十五届联合国大会上,我国向世界做出承诺:力争二氧化碳排放量在2030年前达到峰值,力争2060年前实现碳中和[1]。这一目标的实现迫切需要各行各业加速推进绿色低碳发展。工业、制造业作为我国碳排放的主力军,低碳发展迫在眉睫[2]。在高能耗、高排放的制造业中,纺织行业占有一定比重,其减少碳排放最直接有效的手段应该放在生产阶段[3]。在纺织产品的生产制造过程中,细纱车间的能耗最高,细纱机作为细纱生产加工中的关键设备,其包含的牵伸、加捻及卷绕等装置均是高耗能装置,约占整个流程耗电的62%[4]。细纱机的运行状态、上机工艺参数也直接影响着细纱成纱质量的波动,制约着后续纺织品的产品质量。为此,如何实现细纱生产工艺参数的优化,降低细纱生产加工过程中的能耗,减少碳排放量,同时控制生产工艺参数,提高产品成纱质量,对实现纺织行业绿色低碳发展具有重要意义。
近年来,纺织生产工艺参数优化、降低能源消耗、减少碳排放量,实现纺织工业“绿色纺织、低碳发展”,一直是国内外学者研究的热点内容。Liu等[5]对混纺纱线的水足迹和碳足迹进行评估,从产品设计的源头上进一步减少水的消耗和废水的排放;Tsai[6]针对碳排放、能源回收、废弃物再利用等环境问题,采用作业成本法和约束理论建立数学模型,实现了纺织工业绿色生产计划与控制的目的;Ozturk等[7]通过研究羊毛织物生产设施中的能源效率应用来减少能源消耗和空气排放;Sim等[8]对羊毛地毯和尼龙地毯的能源和碳排放进行了生命周期评估,减轻了能源消耗、碳排放对环境的影响;Diyaley等[9]基于教学的优化算法,确定了环锭纺纱过程中前后区变量和输入变量的最优参数组合,从而生产出具有满意质量特性的纱线。国内学者刘文珊等[10]建立了毛纱工业碳足迹的核算模型,通过核算6类毛纱产品的工业碳足迹值得出:纱线越细,纱线生产工艺越复杂,对应工业碳足迹值越大;王晓峰等[11]研究了纺织企业和品牌商构成的两级供应链模型与加入回收商进行回收再利用的三级供应链2种模型下的节能减排策略;顾燕等[12]通过对纺纱锭速、捻系数等工艺参数进行正交试验,从而确定最优工艺配置,为纺织行业生产高质量产品提供了依据;王青等[13]通过数学建模,得到主牵伸区中二皮辊和二罗拉横向距离的最佳调整位置,为实际生产中并条机牵伸机构工艺调整提供了理论指导;吴震宇等[14]分析了捻接压力、退捻时长以及纱头重叠长度对捻成纱强力保持率的交互影响规律,根据构建的响应曲面模型得出了最优工艺参数组合,按优化后工艺参数进行配置生产出的纱线质量得到提高。
综上所述,针对纺织行业节能降耗进行工艺参数优化,提高纺织产品质量,是实现纺织行业绿色低碳经济长远发展的必要前提。但现有文献针对纺织生产过程中碳排放量、提升产品质量的设计研究基本上处于单一研究,考虑降低纱线生产加工过程中碳排放量并提高成纱质量的研究较少。为此,本文从细纱生产工艺流程出发,提取影响碳排放以及成纱质量的关键可控工艺参数,构建基于非支配排序遗传算法NSGA-II(nondominated sorting genetic algorithm II)的工艺参数优化模型,以保证细纱成纱质量的同时降低细纱生产过程的碳排放量。
1 优化目标及参数确定
1.1 确定优化目标
细纱工序是纺织生产过程中的关键工序,纱线生产过程常常伴随着纱线条干不匀、纱线断头、偶发性粗节、棉结、毛羽等成纱质量的问题,细纱成纱质量的好坏,直接决定着后续纺织品的生产质量,也影响着最终纺织产品的性能,细纱质量的提高对提高纺织品质量发挥着重要作用。细纱车间是纺纱厂用电最多的车间,在目前绿色制造大背景下,如何降低细纱工艺尤其是细纱机的能耗,一直是纺纱厂探讨的重要课题[15],因此,以提高细纱生产过程中成纱质量、降低碳排放量为优化目标要进行多目标优化,即:
(1)
式中:Q表示综合质量指标,由条干CV值、断裂强度、细节、粗节、棉节及毛羽6个质量指标z1~z6转化而成;Ce表示碳排放量,kg;e为各类能源;x1~x7分别表示锭子速度、后区牵伸倍数、捻系数、前罗拉速度、钢领直径、钳口隔距以及前罗拉隔距参数。
1.2 关键指标确定
1.2.1 工艺参数
细纱工序的主要目的是牵伸、加捻及卷绕成型,其中牵伸、加捻和卷绕机构是反映细纱机运行状态、影响细纱成纱质量的重要装置。细纱机能耗的降低、碳排放的减少以及细纱成纱质量的提高,与细纱机牵伸、加捻及卷绕工艺密切相关。细纱机牵伸装置与牵伸工艺参数的优化能够提高细纱机的运转效率,降低能耗的产生,能够提高纱线的加捻效率,有效改善细纱条干均匀度、减少毛羽的产生[16],其涉及的工艺参数主要包括:后区牵伸倍数、前罗拉速度、钳口隔距、前罗拉隔距。细纱机的加捻卷绕工艺的优化可降低生产过程中的断头率,提高成纱质量,其涉及的工艺参数主要包括:锭子速度、捻系数、钢领直径。
1)后区牵伸倍数的配置直接影响着细纱条干均匀度,后区牵伸倍数过小时,容易导致细纱牵伸不开,过大时,容易造成细纱的分布结构恶化。因此,合理配置后区牵伸倍数,增强其稳定性,能有效改善成纱质量的波动。
2)前罗拉速度过大,容易造成纱线过度牵伸,导致纱线断头率增加,前罗拉速度过小,容易造成纱线堆积,产生松纱。
3)钳口隔距制约着牵伸时纱线的运动,其设置是否合理关系到细纱“硬头”现象的产生,合理配置钳口隔距的大小,能够有效改善细纱“硬头”。
4)前罗拉隔距的大小决定了浮游长度,从而影响胶圈对纤维的握持力,进而影响纱线条干均匀度和产品的外观质量。
5)锭子是细纱机加捻卷绕过程中的重要组件。随着锭子转速的增大,加捻卷绕过程中的空气阻力也随之增大,细纱与钢领、钢丝圈之间的摩擦力增大,从而导致细纱机所消耗功率增大以及纱线毛羽增加。
6)在合理范围内,增加细纱捻系数,细纱的捻度也增加,有利于将边缘纤维加捻到纱条内部,外侧的纤维能够很好地被束缚,有利于提高细纱的断裂强度、减少毛羽[17]。
7)钢领是细纱加捻卷绕过程中的重要器材,常与钢丝圈配合使用,选择适当的钢领能够降低与钢丝圈之间的滑动摩擦力,减少发热从而降低细纱机能耗。
基于此,选择锭子速度、后区牵伸倍数、捻系数、前罗拉速度、钢领直径、钳口隔距、前罗拉隔距为关键工艺参数,探寻其与综合质量指标Q与细纱碳排放量之间的关系。以比较典型的“7.29 tex”纱线为例,具体的工艺参数为:锭子速度13 423 r/min、后区牵伸倍数1.16、捻系数354、前罗拉速度154 r/min、钢领直径38 mm、钳口隔距2.5 mm及前罗拉隔距18 mm。
1.2.2 细纱质量指标
衡量成纱质量的指标众多,为提取影响细纱成纱质量的关键指标,以咸阳纺织集团有限公司为例,以纺纱车间生产统计管理系统中的纱线质量管理子系统为基础[18],以细纱车间的典型品种JC7.29 tex为对象,以20 d 2个班(三班两运转)的质量数据为例,从构建的数据存储系统中选取20组质量波动较大的纱线实际生产数据,包括单强CV值、百米质量偏差、条干CV值、粗节、细节、棉结、毛羽、单纱强力及纱线断裂强度9个纱线质量波动指标,采用熵权法(其权重越大,所反映的数据离散程度就越大,在评价质量的过程中起到的作用也越大)对影响质量波动的相关指标进行分析,指标如表1所示。

表1 JC7.29 tex质量指标Tab.1 JC7.29 tex quality indicators
由表1可知,在衡量成纱质量的指标中,条干CV值、断裂强度、毛羽及粗节、细节、棉结对成纱质量影响较大。基于此,选取纱线断裂强度、棉结、粗节、细节、条干CV值、毛羽作为评估细纱成纱质量的关键指标。
1.2.3 细纱碳排放量核算
根据纺织生产半成品、工艺参数指标、能源等输入量与细纱生产加工处理过程以及输出合格的细纱产品间的“输入-处理-输出”关系,建立如图1所示的细纱工序碳排放计量模型。
对细纱生产工艺流程,定义In为细纱工序碳排放计量模型的输入量(包括粗纱半制品、能源等),On为细纱工序质量输出量,En为第n类能源的碳消耗量,fn为第n类能源消耗对应的碳排放系数。Ce为细纱工序生产过程中的碳排放量。在图1的基础上,建立式(2)所示的细纱工序生产过程碳排放函数。

图1 细纱工序碳排放计量模型Fig.1 Carbon emission metering model of spinning process
(2)
式中:Ce为细纱工序生产过程中的碳排放量,kg;Ee为生产过程中各项能源的碳消耗量,kg(以1 kg的CO2碳含量为标准计量);fe为各项能源消耗对应的碳排放系数。
2 多目标优化
2.1 多目标优化总体设计
基于NSGA-II的细纱工艺参数多目标优化,总体设计流程图如图2所示,步骤如下。

图2 基于NSGA-II的细纱工艺参数多目标优化流程图Fig.2 Multi-objective optimization flow chart of spinning process parameters based on NSGA-II
步骤一:细纱机工艺参数选取与关键质量指标确定。分析细纱机运行机制,选取待优化的工艺参数,分析采集数据,确定关键质量评价指标数据。
步骤二:基于信噪比的稳健性设计与CRITIC(criteria importance though intercrieria correlation)赋权的灰色关联度分析。对关键质量评价指标数据进行稳健性处理,并用CRITIC对指标赋权重,再利用灰色关联分析法确定综合质量指标Q。
步骤三:多元非线性响应曲面回归建模。确定模型的目标函数、约束条件,借助Design Expert软件对变量进行训练拟合,建立多目标二阶响应曲面回归模型。
步骤四:NSGA-II多目标遗传算法优化。利用NSGA-II算法对多目标优化数学模型进行优化,得到Pareto最优解。
步骤五:模型验证与分析。对所建立的多目标优化模型、NSGA-II算法寻优的Pareto解进行实验验证分析。
2.2 综合质量指标的确定
2.2.1 基于信噪比的稳健性设计
为使关键质量评价指标趋于强稳健性,常用信噪比(signal-to-noise ratio,S/N)来对质量评价指标进行处理,通过信噪比处理过的质量评价指标不易受到干扰。信噪比分为望大特性、望小特性和望目特性3种,由于在一定范围内,细纱质量指标条干CV值、细节、粗节、棉结及毛羽越小越好,因此选择望小特性的信噪比公式(3)进行相应的转换。
(3)
式中:aS/N为转换后的条干CV值、细节、粗节、棉结及毛羽的信噪比值;n为每组试验重复的次数;yi为第i次试验的质量指标值。
细纱断裂强度指标在一定范围内越大越好,所以选择望大特性的信噪比公式(4)进行相应的转换。
(4)
式中:bS/N为转换后的细纱断裂强度指标的信噪比值;n为每组试验重复的次数;yj为第j次试验的细纱断裂强度指标值。
试验设计过程中涉及的指标数据多,需要对质量指标数据进行编码处理,借助Design Expert软件,获取62组试验数据,并根据式(3)、(4)对试验数据信噪比处理,信噪比处理后的数据如表2所示。

表2 细纱质量指标数据信噪比处理Tab.2 SNR processing of spinning quality index data
2.2.2 CRITIC赋权的灰色关联度分析
灰色关联分析是通过分析各因素之间的关联程度,用一个综合的、影响最大的因素表征多个因素的方法,能够实现将复杂因素到单一因素的转化,常被用于解决多目标优化问题以及工艺参数优化问题。
考虑到单一质量指标的优劣往往不能准确衡量细纱成纱质量的好坏,因此,借助灰色关联分析理论,将纱线条干CV值、纱线断裂强度、细节、粗节、棉结以及毛羽这7个质量指标转化为综合质量指标Q,以便于更客观、准确地评价细纱成纱质量的性能。灰色关联分析将多个指标转化为综合指标的过程中,往往是用平均值法为各指标进行权重分配,但在实际的细纱生产过程中,各质量指标之间的重要程度是不同的,因此并不能很好的凸现出各质量指标之间的相对重要程度。因此,为消除各质量指标权重的主观性,准确反映其重要性,借助CRITIC法在目标赋权方面的优势,对各质量指标进行综合赋权。
2.2.2.1数据归一化处理 为消除各质量评价指标之间的差异,需要对信噪比数据进行归一化处理,选用归一化公式(5)计算:
(5)
式中:yij为试验数据信噪比转化处理结果中的第i行第j列的数值;yijmin为表2中质量指标的最小信噪比;yijmax为表2中质量指标的最大信噪比;xij为yij规范化处理后的值。
2.2.2.2确定灰色关联系数 灰色关联系数是信噪比数据规范化处理后的数据与参考序列的关系,采用式(6)计算灰色关联系数。
(6)

2.2.2.3CRITIC赋权重 CRITIC法作为一种客观赋权法,能够避免平均值赋权重而导致综合质量指标的主观性,以对比强度和指标间冲突性来衡量所反映的信息量的大小,其中对比强度用标准差的形式表现,指标间冲突性用相关系数来表示。基于归一化处理后的数据,根据式(7)、(8)分别对质量指标进行信息量处理及客观权重赋值。
(7)
(8)
式中:Cj为各质量指标之间的信息量;Sj为第j个指标的标准差;P为质量指标的个数;rij为各质量指标之间的相关系数;Wj为各质量指标的权重。细纱质量指标的权重结果如表3所示。

表3 细纱质量指标的权重Tab.3 Weight of spinning quality index
2.2.2.4综合质量指标表征 用灰色关联度γj来表征综合质量指标Q,用式(9)计算灰色关联度,其结果如表4所示。

表4 灰色关联度Tab.4 Grey correlation
(9)
式中,γj为综合质量指标值。
2.3 多目标优化模型的建立
2.3.1 试验因素及约束区间确定
响应曲面的试验因素为:锭子速度x1、后区牵伸倍数x2、细纱捻系数x3、前罗拉速度x4、钢领直径x5、钳口隔距x6、前罗拉隔距x7。根据所选工艺参数样本数据,确定待优化工艺参数的取值范围,进而确定综合质量指标和碳排放量多目标优化模型数学表达式如下:
(10)
2.3.2 响应曲面法试验设计
响应曲面法是通过试验设计的空间点,用数学多项式方程来拟合响应变量与输入参数之间的关系,因其能直观的分析出响应变量与输入参数间的函数关系常被用于求解多目标优化问题。二阶响应曲面模型如式(11)所示。其中:xi为输入参数;y为响应变量;β0、βi、βij、βii为二次回归系数;ε为误差项。
(11)
试验因素量纲不同会对试验结果的准确性造成影响,因此需要对试验因素进行水平编码以消除影响,根据公式(10)中试验因素的区间范围,经过变换操作后,结果如表5所示。

表5 试验因素水平编码变换Tab.5 Experimental factor level coding transformation
借助响应曲面常用分析方法Box-Behnken Design设计方法,对试验因素进行水平编码处理,从而获取62组试验数据进行分析,进而构建7因素3水平的响应曲面回归模型,通过模型训练可分别建立细纱工艺参数与综合质量指标、碳排放量之间的非线性关系,部分试验方案及结果如表6所示。

表6 部分试验方案及结果Tab.6 Partial test scheme and results
2.3.3 多目标优化响应曲面模型拟合
选用精度较高的Box-Behnken Design设计方法对综合质量指标Q、碳排放Ce与细纱机的工艺参数(锭子速度x1、后区牵伸倍数x2、捻系数x3、前罗拉速度x4、钢领直径x5、钳口隔距x6、前罗拉隔距x7)之间进行二次多项式拟合,可分别得到所构建的二阶响应曲面回归方程f1(x)、f2(x)表达式为:
f1(x)=-37.329 7-0.001 7x1+42.960 3x2-0.079x3+0.036 4x4+0.293 6x5-0.247 2x6+
0.133 3x7-0.000 4x1x2-0.054 1x2x3-0.010 6x2x4+0.044 6x2x5+0.511 3x2x6-
0.178 63x2x7-0.000 2x3x5-0.000 5x3x6+0.001 3x4x6-0.000 5x4x7-0.007 3x5x6-
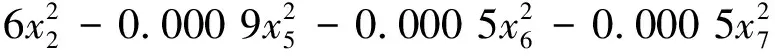
(12)
f2(x)=447.653 3-0.024 1x1-122.983 3x2-1.022 3x3-0.255 3x4+0.184 2x5+10.337 7x6-
4.796 1x7-0.003 3x1x2-0.000 2x1x5-0.000 3x1x6-0.000 2x1x7-0.116 5x2x3-0.050 1x2x4-
2.248 4x2x5-4.460 6x2x6-0.987 7x2x7+0.000 5x3x4+0.003 1x3x5-0.011 4x3x6+0.003x3x7+

(13)
2.4 多目标优化模型寻优
在以往的纺织工艺优化过程中,广泛采用以提升成纱质量或是以减少碳排放量为优化目标的单目标优化方式,亦或是将多目标转化为单目标来达到提高成纱质量和减少碳排放量的目的,而带精英策略的快速非支配排序遗传算法不需要将多目标转化为单目标问题[19],为此,通过带精英策略的快速非支配排序遗传算法来实现细纱工艺参数多目标优化。基于NSGA-II算法的细纱工艺参数设计属于多目标优化问题,各目标之间相互影响、存在矛盾,即在2个目标函数上并非同时存在最优解,其解应为非支配解或者Pareto最优解。
在工艺参数的取值范围内,运用MatLab软件中的gamultiobj函数对待优化的目标函数f1(x)、f2(x)进行求解,其中参数设置为:最大迭代次数200,种群大小100,最优前端个体系数0.3,适应度函数偏差1e-100。对优化模型求解后得到综合质量指标与碳排放量所对应的60组Pareto解集如图3所示。

图3 Pareto最优解集Fig.3 Pareto optimal solution set
由图3可知,随着综合质量指标与工艺参数之间的目标函数f1(x)增加,f2(x)所对应的碳排放量与工艺参数之间的目标函数也随之增加。在Pareto解集中,最右端综合质量指标值大,碳排放量也高;最左端综合质量指标值小,碳排放量也小,可见,碳排放量的降低是以质量指标降低为代价的,而位于中间区域的解属于Pareto最优解,满足了相对小的碳排放量和相对高的综合质量指标2个优化目标,因此,该区域的目标函数折中解可作为工艺参数优化组合。
3 试验验证与分析
3.1 多目标优化模型的拟合性能分析
基于2.3节,借助Design Expert软件对细纱工艺参数与综合质量指标、碳排放进行拟合,得到如图4所示的拟合效果残差概率分布图。可知,建立的多目标优化模型所对应的数据残差概率分布均趋于一条直线两侧,说明建立的多目标优化模型具有良好的拟合性能。

图4 模型拟合性能分析Fig.4 Model fitting performance analysis. (a) Residual probability distribution of f1(x);(b) Residual probability distribution of f2(x)
为进一步验证回归方程f1(x)、f2(x)的显著性,使用方差分析检验回归模型能否显著反映工艺参数与目标函数之间关系,模型的方差分析如表7所示。

表7 回归方程显著性分析Tab.7 Significance analysis of regression equation
由表7可知,2个模型的F检验值分别为15.56和52.89,且对应的显著性水平P值均小于0.000 1,表明回归模型的拟合效果显著。其次,2个模型的决定系数R2分别为0.954 4和0.986 1,其值非常接近1,进一步表明该回归模型具有良好的拟合优度,能用该回归方程表示工艺参数与优化目标之间的规律。
3.2 多目标优化结果分析及验证
NSGA-II算法优化后得到60组Pareto最优解,从解集中选取2组优化解来验证优化模型的有效性。基于咸阳某纺织企业试验平台,以纺织JC7.29 tex细纱工艺为例,结合表8中多目标优化后得到的FA507细纱机加工工艺参数,与企业现有的传统工艺参数进行对比分析,评价指标优化前后对比值如表9所示。

表8 工艺参数优化结果Tab.8 Optimization results of process parameters

表9 评价指标优化前后对比值Tab.9 Ratio of evaluation indexes before and after optimization
结合表8、9可知,通过试验对比分析可知,基于NSGA-II的细纱工艺参数多目标优化优选出的2组优化解所生产出的各项评价指标值较初始值均得到提高。对于碳排放量指标,在优化后的工艺下,优化解分别改善7.24%和4.3%;对于质量评价指标,细纱平均条干均匀度、断裂强度、毛羽等质量评价指标均得到改善,所生产出的细纱结构均匀,不易产生毛羽、断头,具有良好的外观质量。
4 结 论
基于NSGA-II的细纱工艺参数多目标优化方法,考虑了细纱生产加工过程中的成纱质量及碳排放问题,利用CRITIC赋权的灰色关联分析方法将影响细纱质量的各因素转化为综合质量指标,并构建了多目标响应曲面优化模型,采用NSGA-II算法对模型求解得到最优解并对其试验验证,结果表明当工艺参数为:锭子速度12 822 r/min、后区牵伸倍数1.17、捻系数366、前罗拉速度194 r/min、钢领直径35 mm、钳口隔距3.5 mm、前罗拉隔距17 mm时,细纱生产过程中的碳排放量及各项质量评价指标值较初始值均得到改善,生产出的细纱品质得到提升。

