基于集对分析的SFT特征函数重构及性质研究

崔铁军，李莎莎

（1.辽宁工程技术大学 安全科学与工程学院, 辽宁 葫芦岛 125105; 2.辽宁工程技术大学 工商管理学院, 辽宁葫芦岛 125105）

任何系统存在的意义在于完成规定时间内、规定条件下的预定功能。完成该功能的能力称为可靠性，反之为失效。系统具有可靠性的状态称为可靠状态，反之称为失效状态。可靠与失效是对于系统功能而言的，可靠和失效状态组成了系统功能状态；两者组成了功能状态的全集，之间没有交集，但可相互转化。因此系统可靠性的变化可理解为系统功能状态在不同因素影响下可靠状态与失效状态的转化过程。系统功能状态至少包括可靠和失效两种状态。进一步的，在实际的系统功能状态研究中，更多的是难以判断的功能状态，无法确定功能状态归属，即未知或不确定状态。这种情况下系统功能状态至少包括可靠、不确定和失效3种状态。虽然将系统功能状态表示为多状态的叠加方式更具灵活性且反映了真实情况，但如何表示这种系统功能状态成为首要问题。

关于系统功能状态、可靠和失效的表示和研究已有一些。这些研究包括：车辆系统机电设备故障监测及诊断[1]、电池储能系统BMS的功能安全分析[2]、恶劣环境风光互补电路故障诊断[3]、城市轨道交通应急指挥系统功能研究[4]、飞行器电源系统故障可观测性研究[5]、列控系统等级转换场景功能安全分析[6]、控制功能失效的微电网系统可靠性评估[7]、智能变电站保护与控制障碍诊断与预测[8]、核电厂安全级仪控系统设计[9]、设台车液压系统动态特性及故障诊断[10]等。这些研究一般针对具体行业，由于这些行业各具特点，因此方法缺乏通用性，难以形成连贯的理论方法体系。

综上所述，系统功能状态至少存在2种或3种状态的相互转化关系，这些状态既对立又统一，同时动态转化。这些特征与集对分析思想是相同的。因此基于集对分析的联系数对SFT[11-12]的特征函数进行重构，形成SFT可用的联系数特征函数，从而得到元件故障概率分布和系统故障概率分布。最终讨论了这些分布性质及特征函数运算方式和法则，为基于集对分析重构SFT奠定基础。

1 集对思想与系统功能的同构关系

集对分析是处理系统确定性与不确定性相互作用的数学理论，是我国学者赵克勤[13-14]于 1989年提出的。若用集合表示成对事物中的双方，则该事物就是由两个集合组成的对子，即具有一定联系的两个集合组成的系统称为集对[13-14]。

集对分析建立在两个原理之上，即成对原理和系统不确定性原理。成对原理认为事物成对存在[13-14]，是事物普遍联系和对立统一的另一种说法。系统不确定性原理认为同一事物的宏观层面与微观层面联系在一起进行系统性的研究时将出现不确定性。不确定性首先源于层次划分的相对性和层次边界的模糊性，其次源于系统层次的变化和转化[13-14]。进一步的，确定性和不确定性很可能存在于同一层面中。这样即使研究一个系统的一个层次也会面对确定性和不确定性。在该层之上的层次中，该层次的确定性增加，不确定性降低；下层次中，该层次的不确定性增加，确定性降低。

集对分析中使用联系数表示集对的特征函数，是一种结构函数[13-14]。二元联系数表示为μ=a+bi，其中a+b=1，i∈[−1,1]。a和b称为二元联系数的联系分量，前者为确定联系分量，后者为不确定联系分量，i为b的不确定系数。三元联系数表示为μ=a+bi+cj，其中a+b+c=1，i∈[−1,1]，j=−1。a、b和c称为三元联系数的联系分量，分别为同分量、异分量和反分量，i为b的异分量系数，j为c的反分量系数。进一步可得到无穷元联系数，可参考文献[13-14]的论述。

SFT用于研究系统可靠性与故障之间关系，包括空间故障树理论基础[11-12]、智能化空间故障树[15-17]、空间故障网络[18-22]、系统运动空间与系统映射论[23]。SFT的核心是确定系统中元件故障概率或称为事件发生概率，这里的事件指元件故障，两种说法等效，论文使用元件故障概率（分布）和系统故障概率（分布）表示。确定元件故障概率分布的方法很多，在SFT中主要通过特征函数解决。SFT中的特征函数表示单一因素变化后影响元件故障发生概率的变化规律，再将所有特征函数叠加确定多因素影响下该元件故障概率分布。因此元件故障概率分布表示了该元件的安全与不安全状态、可靠与不可靠状态、非故障与故障状态等的变化特征。考虑元件组成系统的结构，可得到系统故障概率分布，同样可表示系统的安全与不安全状态变化特征。

进一步的，系统功能即为系统预定的能力，为保持系统在预定时间内完成预定功能的能力即为可靠性。因此任何系统完成预定功能称为可靠，不能完成或者完成能力下降称为失效。同时考虑到存在即为系统的哲学观点，而系统存在的意义就是为了完成功能，那么系统存在的关键就是维持可接受的可靠性。这种保持可接受可靠性的状态称为系统功能状态的可靠状态，对应的状态为失效状态。因此系统功能状态是在不同因素影响下可靠状态与失效状态的相互转化。其具有如下特点：可靠状态和失效状态组成了功能状态的全域；可靠状态与失效状态没有交集；可靠状态和失效状态是相互动态转化的。

将系统功能表示为二元联系数μ=a+bi，a表示可靠与失效的确定性分量，b表示功能状态的不确定性分量。或者将a表示成可靠状态分量，b表示失效状态分量。这两种表示都可使用联系数对系统功能状态进行表示。但使用三元联系数更为恰当，即μ=a+bi+cj。文献[18-22]研究表明，系统功能状态的确定实际是困难的，即使在因素确定的情况下也较为困难。考虑如下情况，在测试军用移动通信设备时，100套设备被分配给作战人员同时部署。这些设备相当于同时使用，使用环境相差不多，但不同人员对系统的功能性有不同评价。80人认为系统可靠稳定，5人认为系统功能缺失无法使用，剩余15人则难以判断。这就明显的形成了一种三态系统功能状态空间，即可靠状态、不确定状态和失效状态。因此使用三元联系数更为清晰，a、b和c分别为可靠状态分量、不确定状态分量和失效状态分量。在该例子中，a=80/100=0.8、b=15/100=0.15、c=5/100=0.05，三元联系数为μ=0.8+0.05i+0.15j，二元联系数为μ=0.95+0.05i。当然也可以将可靠与失效状态划分更多层次使用多元联系数描述。

综上可知，集对分析与系统功能分析是同构关系。它们都是两个集合之间的关系，具有全域、不相交和动态转化特征。因此使用联系数描述系统功能状态是可行的。具体的可用联系数重构SFT的特征函数，进而叠加形成元件故障概率分布，最终得到系统故障概率分布。在得到分布后就可通过数学方法研究系统故障的变化规律，即系统功能状态特征和规律。以三元联系数特征函数为例，其优点在于，特征函数形成期间就将可靠状态、不确定状态和失效状态分开。借助三元联系数运算方法，在合成及分析元件和系统故障概率分布时三者特征是分开运算的，所得结果也可以清晰地分辨出不同状态对应结果的影响程度；以往方法则容易混淆在一起。

2 联系数特征函数重构

首先给出SFT中元件故障的特征函数Pi(xn)、元件故障概率分布Pi(x1,x2,···,xN)、系统故障概率分布PT(x1,x2,···,xn)。

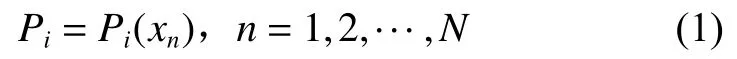
式中：xn表示第n个因素；N为因素总数；i表示第i个元件。

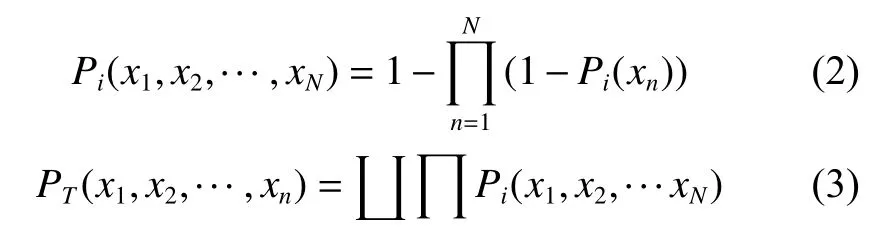
式(1)是重构研究的基础，实际上确定某元件对于某因素的特征函数的方法很多，包括简单的拟合方法[11-12]、因素投影拟合法[24]、模糊结构元方法[25]、云模型方法[13]、神经网络方法[26]等。这些方法各具特点，根据不同数据使用不同方法，但它们都使用了复杂的数学模型并需要大量数据。这对于实际，特别是现场数据的收集提出了很高要求。

由第1节论述可知，集对分析方法的基本思想与系统功能状态是同构的，可使用联系数表示系统功能状态，即使用联系数表示可靠状态、不确定状态和失效状态。而第1节实例也表明这3种状态分量的具体数据是较容易获得的。因此可使用联系数重构SFT的特征函数，形成联系数特征函数。这种特征函数具备了集对分析的同异反状态，分别对应了可靠、不确定和失效状态，具体定量化也相对简单。使用联系数重构特征函数为

式中：Rn表示可靠的元件数；Fn表示失效的元件数；Un表示不确定状态的元件数；Nn表示元件总数，Nn=Rn+Fn+Un；ln表 示 不 确 定分 量系 数 ，ln∈[−1,1]；jn表示失效分量系数，jn=−1。

考虑多因素同时作用于单一元件，将式(4)代入式(2)，得到元件故障概率分布的联系数表示为

进一步的，将式(5)代入式(3)得到系统故障概率分布的联系数表示为

式(4)~(6)是重构的基于集对分析方法的SFT特征函数（联系数特征函数）、元件故障概率分布和系统故障概率分布，是构建基于集对分析的SFT方法的基础。

3 联系数特征函数的性质与基本运算

如式(5)所示，可知元件故障概率分布使用联系数表示后，其分布与可靠分量系数无关，同时失效分量系数变为2倍，又因为ln∈[-1,1]，因此有

在SFT的基本运算中，涉及特征函数的加法、乘法、积分和微分等形式。

联系数特征函数的加法为

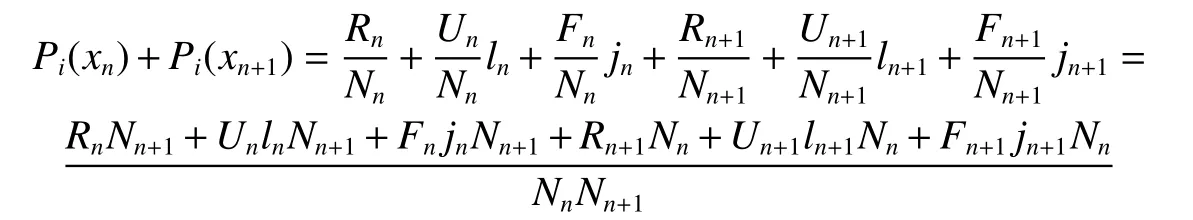
转化为确定不确定的表达方式为

联系数特征函数的乘法为

转化为确定不确定的表达方式为

上述的计算方法来源于三元联系数的计算法则，读者可参考文献[13-14]确定进一步的运算规则和法则。对于联系数特征函数的积分和微分可按照一般代数形式处理，异分量系数i和反分量系数j在运算过程中不变。甚至可以对i和j求偏导研究系统功能状态随着不确定性变化的变化规律。

将上述理论应用于实际问题的过程，较原有方法更为简单。应用的关键是确定式(4)中的各参数，而不需要使用解析方法确定函数。式中ln和jn是固定的 或 具 有范围值；Rn、Fn和Un分 别 表示可靠、失效和不确定状态的元件数，可通过对元件故障过程的统计获得，例如第1节给出的例子；Nn为Rn、Fn和Un之和。所以只要掌握故障元件分类后各状态的数量即可实施上述分析过程。

本文论述了使用集对分析的联系数重构SFT特征函数的方法。从确定和不确定角度，可表示为二元联系数，前项为可靠和失效分量系数和，后项为不确定状态分量系数。从系统功能状态角度，可表示为三元联系数，前项为可靠分量系数、中项为不确定分量系数，后项为失效分量系数。对于系统功能状态的研究，二元联系数具有理论研究意义，研究确定与不确定性关系；三元联系数具有实际研究意义，研究3种功能状态关系。

特征函数是SFT理论的基础。以往特征函数一般通过解析获得，从而建立解析表示方式的SFT。但对于更为广泛的实际故障过程和数据使用解析方法是困难的，而集对分析提供了对故障数据的分类方法，进而确定具有统计意义的特征函数。这种特征函数虽然不及解析方法准确，但蕴含了故障数据的不确定性。因此通过集对分析构造的特征函数更具有统计意义，基于此重构SFT可使原有各种方法具有该能力，进一步解决系统功能状态的矛盾关系。这些方法的重构也是进一步需要展开的研究内容。

4 结束语

利用集对分析的联系数重构了SFT特征函数，为使用集对分析思想研究系统功能状态及建立适应的SFT理论奠定基础。

1）研究了集对分析思想与系统功能状态的关系，认为两者是同构的，集对分析可用于系统功能状态的研究。二元联系数表示系统的确定和不确定功能状态关系；三元联系数表示系统可靠、不确定和失效的功能状态关系。

2）建立了基于联系数的特征函数。使用三元联系数重构了SFT特征函数，并得到了元件故障概率分布的联系数表示及系统故障概率分布的联系数表示。

3）研究了特征函数的性质与基本运算，包括联系数特征函数、元件故障概率分布和系统故障概率分布的一些性质。联系数特征函数的各种运算可参照集对分析中三元联系数的运算方法和法则。