基于ADCIRC的广州市风暴潮精细化预报模型的建立与验证

罗智丰，陈 刚，道付海

(1.广东省水文局广州水文分局，广东 广州 510150；2.广东海启星海洋科技有限公司，广东 广州 511400)

广州市网河区大小水道、河涌纵横交错，水网密布，珠江三角洲出海八大口门占其三：虎门、蕉门、洪奇沥。城区珠江主河段均为感潮河段，据统计，影响广州的台风平均每年2.5个，均给广州带来不同程度的风暴潮灾害[1]。

台风具有发生频率高、受灾范围广、灾害强度大以及次生灾害多等特点[2]，近年来广州风暴潮灾害呈愈发严重的趋势，以广州中心城区代表站——位于海珠区中山大学北门珠江侧的中大站为例，该站历史最高水位排名前6名中，除1次受洪水影响，其余均为风暴潮增水，且均出自2000年之后，0104号“尤特”、0814号“黑格比”、1713号“天鸽”、1822号“山竹”等台风均刷新历史纪录(表1)，尤其“天鸽”“山竹”给广州市带来严重的灾害损失。据统计，“山竹”导致广州南沙、番禺、黄埔、海珠、天河、越秀、荔湾、白云等区共68处堤防浸水，黄埔区江水越堤水浸达15 km，越秀区珠江前航道二沙岛区域江水越堤水浸达7.6 km，受淹车库54个(数据来源：广州市三防办)。

表1 中大站实测最高水位排名(珠江基面) 单位：m

因此，构建广州市风暴潮精细化预报模型，形成面对对象的风暴潮精细化预报，提高风暴潮实时观测与业务化预警报能力，对摸清广州市风暴潮特性、重点保障目标排查，大力提升风暴潮灾害综合防御能力具有重要意义。

1 ADCIRC模型介绍

ADCIRC(An Advanced Circulation Model For Oceanic,Coastal And Estuarine Waters)是由美国北卡罗来纳大学的 R.A.LUETTICH和美国圣母大学的J.JWESTERINK 于1992年研制的基于有限元方法，可用于海洋、海岸、河口区域的水动力模式[3]。被美国工程兵部队(ACE)和美国海军研究所(NRL)广泛应用于各个军港的潮汐、海流和风暴潮的预报中，ADCIRC也被NOAA应用于美国东海岸的风暴潮预报及路易斯安那州的风暴潮风险评估中。近年来，国内许多学者也将其应用于中国沿海的风暴潮数值模拟，刘克强等[4]构建了适用于西北太平洋海域的风暴潮预报模型，李欢等[5]将其应用于宁波沿海风暴潮预报，陈海军等[6]建立了渤海高分辨率的二维潮汐潮流模型，罗锋等[7]建立了江苏海域的精细化风暴潮数值预报模型。

ADCIRC有以下特征：采用广义波动连续方程(GWCE)与动量方程结合，基于伽辽金有限元方法求解；可应用笛卡尔坐标或球坐标、进行二维或三维的计算，并采用并行计算提高计算效率；采用不规则的三角形网格，可精确的模拟河口海岸地区的地形，且可方便地对所关注的区域进行加密，在非关注区域则可以设置较大间距的网格，以节省计算量；采用干湿边界处理技术；可用于计算河堤、海堤等障碍物的溢流计算。

1.1 控制方程

采用垂向平均的二维方式计算[8]，通过笛卡尔坐标下的连续方程和动量方程求解自由表面起伏、二维流速等变量，其二维连续方程为：

(1)

二维动量方程为：

(2)

(3)

式中ζ——从海平面起算的水位高度；U、V——2个方向的垂向平均流速；H——总水深；f——科氏参量；Ps——水面大气压力；ρ0——水密度；g——重力加速度；τbx、τby——底部切应力；τsx、τsy——风应力项；Tx、Ty——波浪辐射应力项；Dx、Dy——扩散项。

为避免和减小伽留金法离散出现的虚假振荡，该模式中连续方程的形式进行了一些处理。将式(1)对时间求偏导数，再将其与连续方程和一个随空间变化的加权函数τ0的乘积相加，整理得到：

(4)

其中Ax、Ay的表达式如下：

(5)

(6)

根据连续方程和动量方程的表达，将Ax、Ay表达为:

(7)

(8)

运用式(7)、(8)中的表达式对式(4)当中的Ax、Ay进行替换，就得到了模式计算中所运用的GWCE(Generalized Wave Continuity Equation)方程[9]。ADCIRC通过对式(2)、(3)、(7)、(8)的联立求解，获得所需的水位和速度值。在球坐标系下进行计算时，利用CPP(Carte Parallelo-grammatique)圆柱法，将坐标投影到笛卡尔坐标系中，然后进行计算。

1.2 底摩擦项

在ADCIRC中，底部应力的表达式为：

τbx≡Uτ*

(9)

τbx≡Uτ*

(10)

其结果依赖于τ*的表达形式。τ*可以采用线性、二次函数或者线性和二次函数的复合公式见式(11)—(15)。摩擦系数Cf则用曼宁系数转化而来，转化关系见式(15)。

τ*=Cf

(11)

(12)

式(11)、(12)中U、V为深度平均速度。

复合形式公式同式(12)，但其中Cf随Hc变化：

(13)

曼宁系数与摩擦系数转化关系：

(14)

式中Hc——临界水深，反映底摩擦在浅水区域增大的一个参数；θ——决定底摩擦系数与渐近线接近的快慢；λ——决定从深水到浅水底摩擦增大的快慢；n——曼宁系数；d——相对于海平面的水深。

2 广州市风暴潮精细化模型搭建

广州市网河区为感潮河段，水位受上游西北江、东江、本地区流溪河、增江来水影响大，因此要准确的模拟该区域河流水动力必须考虑上游来流的影响。分别选取西江的高要、北江的石角、东江的博罗、流溪河的太平场、增江的麒麟咀水位站所在位置为模型的上边界起算点(图 2b)，并以这5个水文站的实测流量作为模型上边界驱动条件，把各个实测流量平均到对应河流上边界的每个网格节点上，以本质边界条件输入模式，即通过在连续方程中指定对法向边界通量积分的非零值和在动量方程中指定非零法向速度来实现的，该边界条件满足全局和每个边界节点处的通量平衡。

风暴潮与潮汐并非是线性的叠加关系，它们存在非线性相互作用，且较严重的风暴潮灾害往往发生在风暴潮遇到潮汐高潮位时，两者的共同作用推高水位，造成危害，因此，对风暴潮与潮汐进行耦合计算，可以使计算结果更加准确。模式的潮汐计算准确与否很大程度上取决于外海开边界上潮位的准确性，很多全球大洋潮汐模式均可通过插值的方式来提供大洋中每个点的潮汐资料比如TPXO7.2、NAO.99b、GOT00.2、DTU10等模式[10]，而郑后俊等[11]采用293个站点的观测资料对各个模式在南海的潮汐预报能力进行分析比较，发现DTU10模式的整体预报效果最好，高秀敏等[12]采用南海海域60个验潮站和22个TOPEX/Poseidon卫星高度计轨道交叉点的调和常数资料，对比了4种模式4个主要分潮调和常数在南海的准确度，表明南海北部和东部区域DTU10的准确度最高。DTU10是丹麦科技大学在2010年建立的全球大洋潮汐模式，它是以FES2004为参考，基于响应法对T/P和Jason-1/2卫星高度计资料进行残差分析而建立的，分辨率为0.125°[13-14]，本文的开边界潮汐资料选用DTU10。南海区域的潮波主要是从太平洋经吕宋海峡传入，本文所建立的模式，计算区域较大，涵盖吕宋海峡和南海中、北部区域，可以更好地模拟超波的传播过程。

外海开边界天文潮位由8个主要的调和分潮(K1、M2、N2、O1、S2、K2、P1、Q1)计算，见式(15)，风场作为下边界条件输入该模型进行计算。

(15)

式中ζ——总水位；a0——平均海面；f——节点因子；H——分潮振幅；V0+μ——分潮的天文初相角；K——分潮迟角；m——分潮个数；i——各个分潮。

白新欢提出马克思共产主义思想具有科学、现实和哲学三个基本维度，其中前两个维度使共产主义成为科学。他同时强调了马克思人道主义思想是共产主义思想的重要出发点。[12]

模型同时考虑上游来水、天文潮、风暴潮的共同作用，既能充分考虑多种因素的共同作用又能提高计算效率，考虑到台风预报信息的精度时效及模型的计算效率，目前模式可实现广州市未来3 d的精细化预报，模型每次运算时间约20 min。模型框架结构见图1。

图1 模型结构

2.1 计算网格

模型采用非结构的三角形网格，可精确的模拟河口海岸地区的地形变化，且可方便地对所关注的区域进行加密，网格步长从外海到近岸逐渐变小，可有效地提高计算效率。为了更好地模拟风暴潮在南海的生成与传播过程，模式的计算范围选择为105.6°E～127°E和13°N～27°N，见图4a(图中颜色表示水深)。因为要在广州市网河区实现风暴潮精细化预报，对于该区域内的河段提高分辨率，见图4b，网格最小分辨率为50 m。

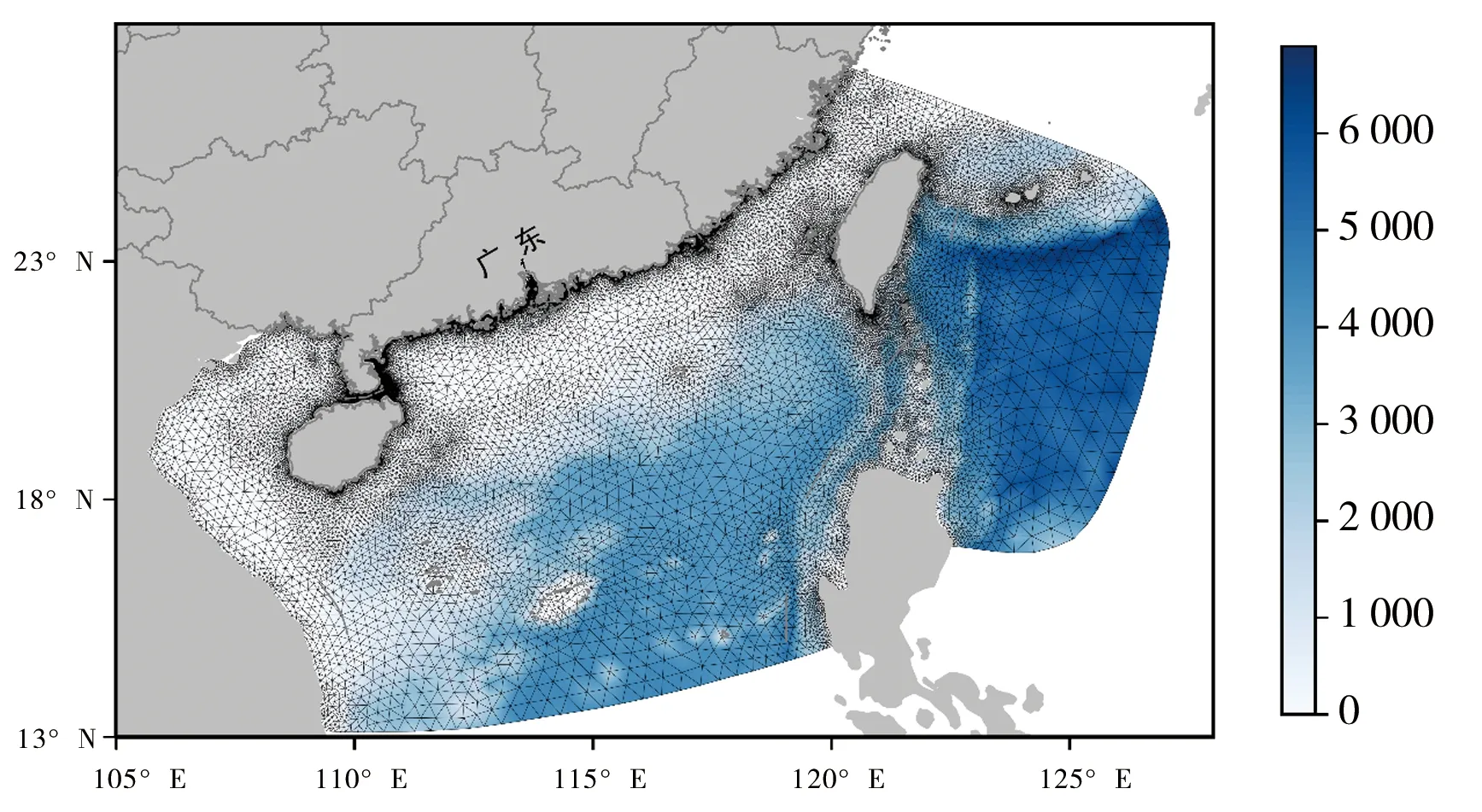
a)海区网格

2.2 台风风场

风暴潮模式结果的准确性在很大程度上依赖于风场模式的质量。本文采用常用的Jelesnianski台风气压模型[15]和风场模型[16]，气压场分布是由压差(Pn-Pc)以及最大风速半径Rmax决定的，其表达式为：

(16)

式中P(r)——距离台风中心r的海表面气压值；Pc——台风中心气压；Pn——台风以外不受干扰的背景气压；Rmax——台风最大风速半径；r——距离台风中心的距离。

Jelesnianski台风风场模型是一种经验模型，直接从风场外观相似性出发建立模型风场，可表示为圆形风场与移动风场的和：

V=Vr+Vs

(17)

其中的圆形风场Vr和移动Vs的表达式分别为：

(18)

(19)

式中Vm——台风最大风速；Vc——台风中心移动速度。

风拖曳系数Cd采用Garratt公式：

(20)

3 天文潮验证

天文潮验证计算的时间段为2019年8月27日到9月30日23时，共计算35 d，前5 d为模式冷启动调整时间，不进行分析。模式结果与国家海洋信息中心发布的潮汐表天文潮结果做比对。选取了珠江口附近城市的6个代表潮位站进行比对，分别为香港、赤湾(深圳)、南沙(广州)、澳门、珠海港、台山(江门)等潮位站。图3为各潮位站计算与发布的天文潮对比曲线。结果显示：各站天文潮计算结果与潮汐表所示潮位的平均绝对误差，最大平均绝对误差小于13 cm(表2)，模型计算结果与潮汐表的天文潮结果基本相符，表明该模型基本可以反映出珠江口沿岸天文潮状况。

a)香港

c)南沙

表2 各站计算天文潮与潮汐表误差比对

4 历史台风暴潮验证

选取刷新广州市多个潮位站历史纪录的典型台风2017年13号台风“天鸽”和2018年22号台风“山竹”(图4)，对广州市风暴潮精细化模型进行了验证。

图4 “天鸽” “山竹”发展路径

台风“天鸽”于2017年8月23日12时50分在珠海市金湾区沿岸以强台风级别登陆，登陆时中心最大风力14级(45 m/s)，给珠三角地区带来严重的风暴潮增水，三角洲多个潮位站出现超百年一遇且破历史极值的高潮位，中大站8月23日15 时45分出现2.76 m的高潮位，超当时历史极值(200814“黑格比”)0.03 m，超警戒1.26 m。1822号台风“山竹”于2018年9月16日17时在广东江门台山市海宴镇登陆，登陆时为强台风级，中心附近最大风力14级，相当于45 m/s。“山竹”给珠江三角洲地区带来了 2.60～3.00 m的风暴潮增水，三角洲地区多个潮位站出现了突破历史记录极值的超百年一遇高潮位，中大站9月16日19 时35分出现3.23 m的高潮位，超历史极值(201713“天鸽”)0.47 m，超警戒1.73 m。

选取广州市南沙区南沙站，番禺区三沙口、三善滘站、大石站，黄埔区黄埔站及海珠区中大站等6个潮位站，对2场强台风的风暴潮进行模拟验证，结果显示模型对各站风暴潮的增水过程、最高水位峰值和出现时间均模拟得较好(图5、6)：“天鸽”台风各站模型计算最高水位误差在12～39 cm，最大相对误差个别站点12.5%，大部分站在10%以内，相位最大误差均在20 min以内；“山竹”台风各站模型计算最高水位误差在0～31 cm，模型相对误差均在10%以内，相位最大误差除三善滘站45 min附近，其余各站误差均不超20 min。具体误差统计见表3、4。

a)南沙

a)南沙

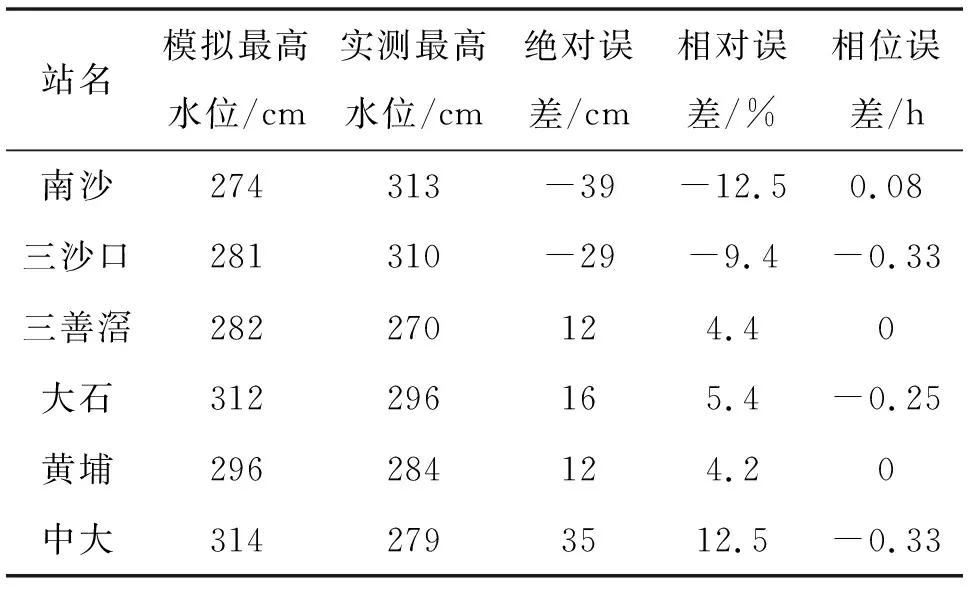
表3 1713号“天鸽”影响期间各站风暴潮模拟误差统计

表4 1822号“山竹”影响期间各站风暴潮模拟误差统计

5 结语

广州市网河区水位影响因素复杂，建立同时考虑上游来水、天文潮、风暴潮共同影响的风暴潮精细化预报模型，并以1713号“天鸽”、1822号“山竹”台风进行验证，结果如下。

a)基于ADCIRC的风暴潮精细化预报模型能较好的反映广州市网河区的天文潮状况，可实现为无实测数据、无潮位站点的河道网格化的天文潮预报。

b)该模型能较好地模拟上游来水、天文潮、风暴潮共同影响的潮区河道总水位，并能较为准确地对广州市网河区风暴潮过程进行模拟，可为未来广州市风暴潮精细化预警预报工作提供参考。