基于BP神经网络和响应面拟合的水工沥青混凝土动态抗压强度预测

辛振科

(1.甘肃省水利水电勘测设计研究院有限责任公司，甘肃 兰州 730000；2.西安理工大学水利水电学院，陕西 西安 710048)

沥青混凝土作为防渗材料被广泛用于水库大坝当中，沥青混凝土防渗体坝也被认为是未来特高坝适宜的坝型。随着水利工程建设的发展，现今拟建或待建的大坝大多位于高海拔、高地震烈度和高寒地区。因此，对水工沥青混凝土在不同温度下的动态抗压强度进行深入研究是水利工程坝工材料领域的迫切需求。文献[1-6]从温度、应变率和尺寸效应3个方面对水工沥青混凝土的动态力学性能和防渗性能等进行了相关的试验研究、理论分析和离散元模拟。然而，试验研究会受到试验条件和时间等各方面的限制，不易全方位展开研究。文献[7-8]对沥青混凝土进行了数值仿真研究。文献[1,3]采用建立数学模型的方法进行了研究。数值仿真结果存在很大的人为影响，数学模型存在精度较低、参数不易确定和适用范围有限等的缺陷。BP神经网络在预测方面具有明显的优势，文献[9-10]采用BP神经网络对砂岩和超高性能混凝土(UHPC)的抗压强度进行了预测，张海发等[11]对原始数据进行小波降噪处理后采用BP神经网络对滑坡变形进行了预测研究，袁可等[12]基于BP神经网络模型对纤维编织网增强自应力混凝土膨胀量的预测方法进行了研究，林智艳[13]采用BP神经网络对土石坝的变形进行了预测。然而，针对水工沥青混凝土的动态抗压强度采用BP神经网络模型预测的研究却鲜有报道。

鉴于此，本文从温度和应变率2个维度设计了32组圆柱体受压试件，得出了水工沥青混凝土的抗压强度数据；建立了2-3-1拓扑结构的水工沥青混凝土动态抗压强度的BP神经网络预测模型；采用建立的BP神经网络模型进行预测，并将预测结果与响应面函数拟合的预测结果进行了对比。

1 试验研究

1.1 配合比及试样制备

根据规范[14]设计本试验水工沥青混凝土级配，配合比见表1。采用克拉玛依70号沥青，沥青含量为7.0 %，圆柱体试件的直径和高度均为100 mm。

1.2 试验方案及加载过程

根据沥青混凝土防渗体坝的工作环境，本文试验温度分别为 -20、-10、-5、0、5、10、20、30 ℃。选取的应变速率分别为10-5、10-4、10-3、10-2s-1。试验设备分别为MTS静动态试验机和高低温环境箱，试验现象和试件破坏图片见课题组已发表文献[1-6]。试验结果数据见表2，表中的抗压强度值为一组3个试件的均值，个别离散性较大的数据进行了剔除，取2个试件的均值，全部试件的抗压强度值见课题组已发表文献[1-6]。图1给出了本文试验研究的32组试件的温度、应变率和抗压强度的3D颜色映射曲面图，从图中可以直观地看出水工沥青混凝土的抗压强度随温度的增大而降低、随应变率的增大而升高。

表2 沥青混凝土动态抗压试验样本数据

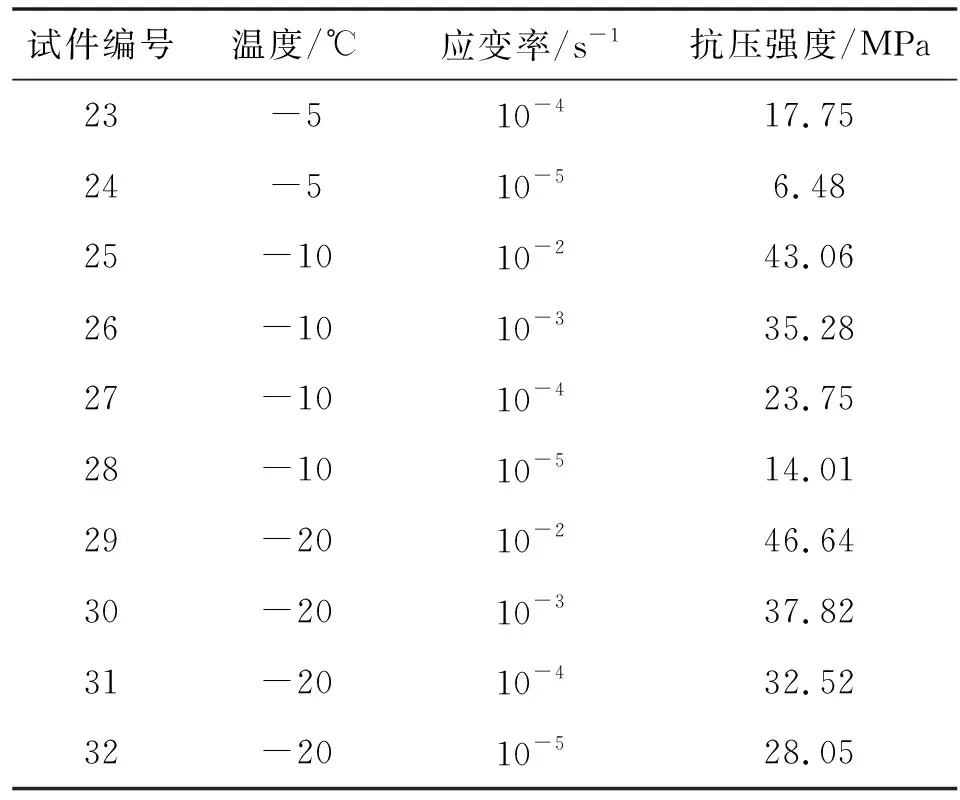
续表2 沥青混凝土动态抗压试验样本数据

图1 试验数据的3D颜色映射曲面

2 BP神经网络预测模型

神经网络是一种机器学习的人工智能算法，通过模仿动物神经网络行为特征，进行分布式并行信息处理。BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络的数学模型，具有很强的非线性映射能力和柔性的网络结构。本文利用32组试验数据作为BP神经网络样本数据，随机抽取6组作为测试样本，剩余的26组作为训练样本，以温度和应变率为输入层，以抗压强度为输出层，隐含层神经元个数M按式(1)计算。BP神经网络的拓扑结构见图2。

(1)

式中n——输入层神经元数；m——输出层神经元数；a0——[1,10]之间的常数。

由式(1)可计算出隐含层神经元数的范围为[3，12]，将隐含层神经元逐次递增并多次试算，得到当隐含层神经元数为3时，预测值与试验值之间的最大相对误差最小，故取隐含层神经元数为3。

图2 BP神经网络模型拓扑结构

3 响应面拟合预测模型

响应面[15]指响应变量Z和一组输入变量(x1，x2…xn)之间的函数关系式，依据响应面法建立的水工沥青混凝土动态抗压强度预测模型可用于试验结果的预测。响应面函数见式(2)。以26组试件的试验数据作为拟合数据，剩余6组作为检验数据，采用麦夸特法(Levenberg-Marquardt)加通用全局优化法的优化算法，经过44次迭代达到收敛，拟合值与试验值之间的均方差(RMSE)为3.163 2，拟合优度(R2)为0.949 3，最终拟合求出的具体响应面函数见式(3)，式中Z表示抗压强度(MPa)；x1表示温度(℃)；x2表示应变率(s-1)。

(2)

(3)

4 预测模型合理性分析

预测结果见表3，BP神经网络模型预测的相对误差均值为-0.80%，响应面拟合模型预测的相对误差均值为 -44.27%。图3和图4分别对BP神经网络模型和响应面拟合模型预测的抗压强度与试验结果进行了可靠性检验，主要对预测结果和试验值之间做了一次多项式拟合并与直线y=x进行对比，可以看出BP神经网络预测模型的可靠性更高。

用相关系数r表征水工沥青混凝土动态抗压强度模型预测结果与试验值之间的相关程度，其表达式为：

(4)

得出BP神经网络模型和响应面拟合模型预测值与试验值的相关系数r分别为1.099 5和1.114 2。说明本文建立的BP神经网络模型预测精度略高于响应面拟合模型。

表3给出了6组试件抗压强度的BP神经网络模型预测值、响应面拟合模型预测值以及对应的试验值。表4对2种模型的预测结果进行了对比，表中PC表示抗压强度预测值(MPa)，PT表示抗压强度试验值(MPa)。可以看出2种预测模型均达到了较高的精度，BP神经网络模型预测精度略高于响应面拟合模型预测结果(图3、4)。BP神经网络模型每次预测结果都略有差异，响应面拟合模型每次的预测结果都唯一，因为响应面拟合模型有具体的函数表达式，而BP神经网络是一个“黑匣子”。

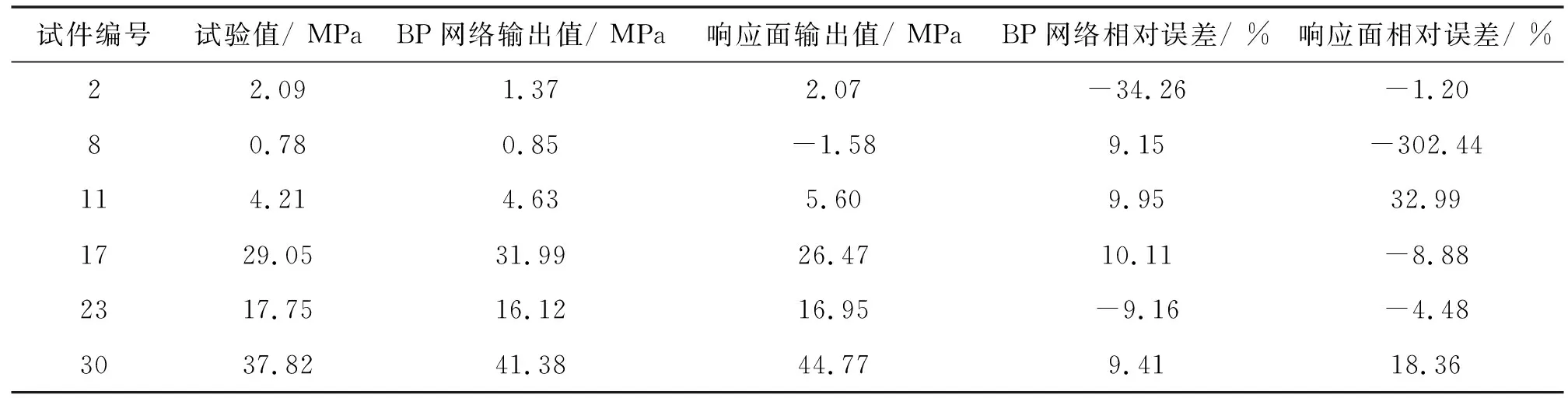
表3 2种模型预测值与试验结果对比

表4 2种预测模型计算结果对比

图3 BP神经网络模型可靠性检验

通过对比BP神经网络模型和响应面拟合模型可以看出，BP神经网络模型在非线性映射预测方面具有非常明显的优势，相较于本文的响应面拟合、文献[1]的时温等效原理拟合、文献[3]的Logistic函数拟合等具有具体函数表达式的数学模型，BP神经网络模型预测优势明显，可以作为相关试验和数值分析的辅助研究手段。

5 结语

a)相较于有具体表达式的响应面拟合模型，BP神经网络模型的预测精度更高，本文建立的BP神经网络预测模型可以作为相关试验研究和数值分析的辅助手段。

b)水工沥青混凝土的受压性能对温度变化敏感，本文样本数据和输入层变量较少，因此还需要大量的试验数据来建立精度更高，适用范围更广的BP神经网络预测模型。