基于奇异谱分析与梯度优化算法优化的RVM、SVM月径流预测研究

梁晓鑫，崔东文

(1.云南省水文水资源局文山分局 云南 文山 661100；2.云南省文山州水务局 云南 文山 663000)

径流时间序列是指月径流数据按照时间先后顺序排列而成的数列，开展径流时间序列分析预测对水文预测预报、水资源开发利用等具有重大意义。水文时间序列影响因素众多、变化复杂，表现出较强的非线性、非平稳性和多尺度等特征，传统自回归类模型、集对分析模型、灰色模型等传统拟线性预测方法存在着局限性，难以获得理想的预测效果[1]。当前，基于“分解—预测—重构”模式的时间序列预测方法被广泛应用于水文时间序列径流预测，并取得较好的预测效果。常见的时间序列分解方法有小波变换(WT)、经验模态分解(EMD)、集合经验模态分解(EEMD)、变分模态分解(VMD)、奇异谱分析(SSA)等方法；预测模型主要有BP神经网络[2-3]、广义回归神经网络(GRNN)[4]、支持向量机(SVM)[5]、相关向量机(RVM)[6]、极限学习机(RELM)[7]等。

为进一步提高水文时间序列预测精度，克服单一模型的不足，本文基于“序列分解—参数优化—分项预测—结果叠加”思想和“奇异谱分析(Singular Spectrum Analysis，SSA)、梯度优化(gradient-based optimizer，GBO)算法、相关向量机(relevance vector machine，RVM)与支持向量机(Support Vector Machines，SVM)”方法，提出SSA-GBO-RVM、SSA-GBO-SVM月径流时间序列融合预测模型。通过SSA对月径流数据进行处理，提取多个独立子序列，达到降低径流数据复杂性的目的；针对RVM核宽度因子和超参数、SVM惩罚因子和核函数参数对RVM、SVM预测性能影响较大以及参数难以选取等问题，采用GBO算法优选RVM、SVM关键参数，达到提升RVM、SVM预测性能的效果；利用云南省龙潭站65年共780个月月径流数据对SSA-GBO-RVM、SSA-GBO-SVM模型预测性能进行检验，旨在验证SSA-GBO-RVM、SSA-GBO-SVM模型用于月径流时间序列预测的可行性和可靠性。

1 SSA-GBO-RVM、SSA-GBO-SVM集成模型

1.1 奇异谱分析(SSA)

SSA依据所观测到的时间序列构造出轨迹矩阵，并对轨迹矩阵进行分解、重构，从而提取出代表原时间序列不同成分子序列[8-10]。SSA包含分解与重构2个阶段。

a)分解。选取窗口长度L构造轨迹矩阵X如下：

(1)

式中M——时间序列长度；L——窗口长度，即嵌入维数，一般为不超过序列长度1/3的整数。

对矩阵X进行SVD(singular value decomposition，SVD)分解：

(2)

式中λi——第i个特征值；Ui——与第i个特征值对应的特征向量；Vi——第i个主成分；d=rank(X)=max{i:λi>0}。

(3)

式中 向量数量K=M-L+1；L*=min(L,K)；K*=max(L,K)。

1.2 梯度优化(GBO)算法

1.2.1GBO算法简述

梯度优化(GBO)算法是Ahmadianfar I 等人受牛顿-梯度下降法启发而提出的一种新型元启发式优化算法。与传统元启发式优化算法相比，GBO算法不但实现简单，设置参数少(仅需设置种群规模和最大迭代次数)，而且具有较好的探索、开发、收敛能力和有效避免局部极值的能力。参考文献[12]，GBO算法数学描述简述如下。

a)初始化。GBO算法中，种群个体被称为“向量”，该“向量”在D维搜索空间中可表示为Xn,d=[Xn,d,Xn,d,…,Xn,d],n=1,2,…,N；d=1,2,…,D，在D维搜索空间中随机生成初始向量Xn表示为：

Xn=Xmin+rand(0,1)×(Xmax-Xmin)

(4)

式中Xmax、Xmin——搜索空间上下限值；rand——[0,1]范围内随机数。

b)梯度搜索规则(GSR)。GSR规则可以帮助GBO算法在优化过程中解决随机行为，从而促进探索并避免局部最优；运动方向(DM)用于创建合适的局部搜索趋势，以提高GBO算法的收敛速度。梯度搜索规则(GSR)与运动方向(DM)数学描述如下：

(5)

(6)

GBO算法第m+1次迭代向量位置更新描述如下：

(7)

其中，

(8)

(9)

(10)

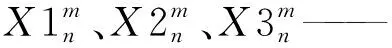
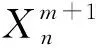
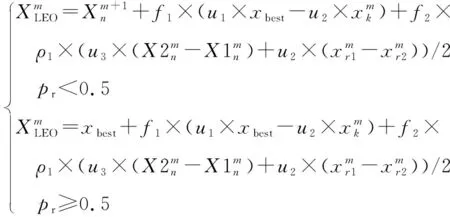
(11)

(12)

式中f1——[-1,1]范围内随机数；f2——平均值为0、标准差为1的正态分布随机数；pr——概率；u1、u2、u3——3个随机数；其他参数意义同上。

1.2.2GBO算法仿真验证

选取6个典型测试函数在不同维度条件下20次寻优平均值对GBO算法寻优性能进行评估，并与文献[11]海洋捕食者算法(MPA)、粒子群优化(PSO)算法的仿真结果进行比较，结果见表1。实验参数设置如下：GBO、MPA、PSO算法群体规模N=100，最大迭代次数M=500，其他采用算法默认值。

表1 函数优化对比结果

a)对于单峰函数，GBO算法在不同维度条件下寻优精度分别较MPA和PSO算法提高113、88、61和134、102、 68个数量级以上，具有较好的寻优精度。

b)对于多峰函数Griewank、Rastrigin、Ackley，GBO算法在不同维度条件下20次寻优均获得了相对理论最优值0和8.88e-16，寻优精度略优于MPA，远优于PSO算法，具有较好的全局搜索能力。

可见，GBO算法对上述6个测试函数均具有较好的寻优精度和全局搜索能力。

1.3 相关向量机(RVM)

RVM是一种基于贝叶斯推理的稀疏概率机器学习模型，其基本算法简述如下[13-16]。

(13)

(14)

式中t=(t1，t2，…，tN)T；Φ——N×(N+1)的核函数矩阵。

为避免ω和σ2过拟合，常使用零均值高斯先验概率分布约束参数：

(15)

式中α——一个N+1超参数向量。

基于贝叶斯公式，后验分布的权重描述为：

(16)

式中μ=σ-2∑ΦTt；∑=(σ-2ΦTΦ+A)-1；A=diag(α0,α1,…,αN)。

为建立统一的超参数，p(t|α,σ2)定义如下：

(17)

本文利用高斯径向基核函数(RBF)作为核函数，即：

(18)

式中d——核函数宽度因子。

1.4 支持向量机(SVM)

设含有l个训练样本的集合为{(xi，yi)，i=1，2，…，l}，xi(xi∈Rd)为第i个训练样本输入列向量，yi∈R为对应输出值[17-18]。则SVM在高维特征空间中建立的线性回归函数为：

f(x)=wΦ(x)+b

(19)

式中Φ(x)——非线性映射函数；w——超平面的法向量；b——超平面的偏移量。

(20)

选择径向基核函数作为SVM核函数，径向基核函数表达式为：

(21)

式中g>0。

1.5 SSA-GBO-RVM、SSA-GBO-SVM建模流程

SSA-GBO-RVM、SSA-GBO-SVM建模预测实现流程见图1，实现步骤如下。

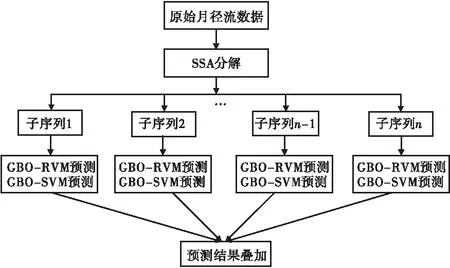
图1 实例月径流预测流程

步骤一采用SSA方法将原径流序列分解为多个独立的子序列；通过自相关函数法(Autocorrelation Function Method，AFM)确定各子序列输入向量，合理划分训练样本和预测样本。

步骤二构建适应度函数：

(22)

图2 奇异谱分析分解图与原始月径流量

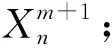
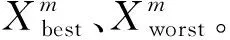
步骤八分别利用GBO-RVM、GBO-SVM模型对各子序列进行预测，预测结果叠加即得到实例月径流预测的最终结果。

步骤九分别采用平均绝对百分比误差(mean absolute percentage error，MAPE)、平均绝对误差(mean absolute error，MAE)和纳什系数(Nash-Sutcliffe efficiency coefficient，NSE)对各预测模型有效性进行评估，见式(23)。

(23)

2 实例应用

2.1 数据来源

龙潭站系红河流域泸江水系盘龙河干流控制站，控制径流面积3 128 km2，为国家重要水文站和中央报汛站。盘龙河发源于红河州蒙自县鸣鹫乡，流经西畴、马关、麻栗坡于天保船头附近注入越南，河长252.6 km，平均坡降8.73‰，中越国界以上流域面积6 497 km2，多年平均径流量为26.93亿m3。本文数据来源于龙潭站1952年1月至2016年12月实测月径流序列，月径流量变化过程见图2。

2.2 SSA分解

SSSA分解确定子序列数量至关重要，若子序列数量过少，则不足以将原始序列中蕴含的不同成分提取出来；若子序列数量过多，则增加了模型复杂程度和建模工作量[8]。由于水文气象是以年为周期，因此本文设置窗口长度L=12，即利用SSA方法将原月径流时间序列数据分解为12个独立的子序列，利用SSA-GBO-RVM、SSA-GBO-SVM模型分别对12个子序列进行预测，将预测结果叠加后得到最终预测结果。SSA分解与月径流随时间变化趋势见图2。从图2可以看出，子序列1振幅最大、频率最高、波长最短，大致反映了原月径流时间序列的变化趋势；子序列2—12振幅逐渐减小、频率逐渐降低、波长逐渐变长，反映了原径流时间序列的波动情况。

2.3 确定输入向量

本文采用AFM法确定各子序列的输入向量，通过计算各子序列逐月径流数据序列的自相关系数，将自相关系数最大时所对应的滞后数Y作为各子序列的最优嵌入维数，即将预测月的前Y个径流量数据作为输入向量，预测月作为输出向量，见表2。本文利用实例后120个月作为预测样本。

表2 各子序列自相关系数、嵌入维数及序列长度

2.4 参数设置及预测分析

2.4.1参数设置

SSA-GBO-RVM、SSA-GBO-SVM模型参数设置为：GBO算法种群规模N=50，最大迭代次数M=100；核函数选择径向基核函数RBF。其中，RVM超参数和核函数宽度因子搜索范围均设置为[-10,10]；SVM惩罚因子、核函数参数搜索范围均设置为[0.01,100]，交叉验证折数设置为3，不敏感损失系数设置为0.01，原始数据采用[-1,1]进行归一化处理。

2.4.2月径流预测及比较

利用SSA-GBO-RVM、SSA-GBO-SVM模型对实例子序列1—12进行训练及预测，将结果进行叠加即得到实例月径流训练及预测的最终结果。采用平均绝对百分比误差MAPE、平均绝对误差MAE和纳什系数NSE对各模型性能进行评估，结果见表3；训练及预测效果见图3—6。

表3 实例136个月月径流预测结果对比表

图3 SSA-GBO-RVM模型训练效果

图4 SSA-GBO-RVM模型预测效果

图5 SSA-GBO-SVM模型训练效果

图6 SSA-GBO-SVM模型预测效果

依据表3及图3—6可以得出以下结论。

a)SSA-GBO-RVM、SSA-GBO-SVM模型对实例月径流时间序列拟合的MAPE分别为5.74%、5.69%，MAE分别为1.10、1.14 m3/s；预测的MAPE分别为6.20%、7.82%，MAE分别为0.88、1.00 m3/s，均具有较好的拟合、预测效果。表明SSA方法能有效将原径流时间序列数据分解成多个更具规律的子序列，GBO算法能有效优化RVM核宽度因子和超参数、SVM惩罚因子和核函数参数，基于序列分解—参数优化—分项预测—结果叠加思想构建的SSA-GBO-RVM、SSA-GBO-SVM模型均具有较高的预测精度，将其用于水文时间序列预测是可行的。其中，SSA-GBO-RVM模型预测效果要优于SSA-GBO-SVM模型。

b)SSA-GBO-RVM、SSA-GBO-SVM模型对实例训练样本、预测样本拟合、预测达到水文预报甲等精度等级的比例(相对误差绝对值小于等于20%)分别均为96.9%、99.2%，满足水文预报精度要求，均具有较好的预报效果。

c)SSA-GBO-RVM、SSA-GBO-SVM模型对实例训练样本、预测样本拟合、预测的纳什系数NSE分别高达0.994 8、0.993 9和0.992 6、0.991 3，表明SSA-GBO-RVM、SSA-GBO-SVM模型用于月径流时间序列预测可信度较高。其中，SSA-GBO-RVM模型可信度最高。

d)从图3—6来看，SSA-GBO-RVM、SSA-GBO-SVM模型对实例月径流时间序列拟合、预测的效果均较好，除少数样本的相对误差、绝对误差较大外，绝大多数样本的拟合、预测结果较接近实测值，满足预测精度要求。其中，SSA-GBO-RVM模型预测结果更接近实测值，相对误差更小、预测效果更佳。

3 结论

本文基于序列分解—参数优化—分项预测—结果叠加思想构建SSA-GBO-RVM、SSA-GBO-SVM时间序列集成模型，通过云南省龙潭站月径流时间序列预测实例对SSA-GBO-RVM、SSA-GBO-SVM模型进行检验，得到以下结论。

a)通过6个单峰、多峰函数在不同维度条件下对GBO算法进行仿真验证，并与MPA、PSO算法比较。验证了GBO算法具有较好的寻优精度和全局搜索能力。将GBO算法用于RVM核宽度因子和超参数、SVM惩罚因子和核函数参数寻优是可靠的。

b)SSA-GBO-RVM、SSA-GBO-SVM模型对实例月径流时间序列均具有较好的拟合、预测效果，模型具有较高的可信度，将其用于水文时间序列预测是可行的。其中，SSA-GBO-RVM模型优于SSA-GBO-SVM模型。

c)实例验证表明，SSA方法能有效将原径流时间序列数据分解成多个更具规律的子序列，抽取出径流序列的整体趋势和不同周期上的波动情况；GBO算法能有效优化RVM核宽度因子和超参数、SVM惩罚因子和核函数参数；基于序列分解—参数优化—分项预测—结果叠加思想构建的SSA-GBO-RVM、SSA-GBO-SVM模型在水文时间序列径流预测中均具有较高的预测精度和可信度。