基于Morgenstern-Price法的二元结构滑坡反演分析

韩 羽， 聂 鹏， 湛 杰， 陈思瑶

(中水珠江规划勘测设计有限公司，广东 广州 510610)

边坡稳定问题在水利水电工程勘察设计过程中比较突出，其对工程建设及运营均有较大影响。边坡稳定性分析方法分为定性法和定量法，如利用河谷地质结构的控制作用对边坡稳定性进行初判，再“先建假设模型，后做勘察验证”的方法[1]和利用赤平投影分析的图解法都属于定性分析法；极限平衡法和数值仿真法为定量计算法[2]。定量计算需要可靠的岩土体参数作支撑，岩土体参数通常采用室内试验、原位测试等方法获取，但岩土体参数受取样条件、应力场等边界条件影响较大，通过试验等方法难以获得准确的、代表性强的抗剪强度参数[3-4]，因此，通过反演分析获得岩土体参数的方法受到研究者的重视。张艳玲等[5]利用基于拉格朗日有限差分法建立的DAN-W动力模拟方法，反演模拟碎屑流运动过程，所得结果与实际情况吻合度较高。蒋水华等[6]利用DREAM(zs)、BUS 和aBUS等3 种可解释岩土力学参数空间变异性的参数随机反演方法，从随机样本产生方式、收敛判据、模型证据和后验失效概率计算等方面进行了比较。燕彦君等[7]利用ANSYS有限元软件对铁路高边坡岩土体参数反演分析并与实际监测位移曲线拟合得出岩土体最优参数。杨仲康等[8]针对金沙江白格“11·3”滑坡，采用基于极大似然估计的优化算法，对滑坡岩土体的抗剪强度参数进行了反演分析；并利用反演参数，采用蒙特卡洛方法对滑坡后缘裂缝区进行了可靠度计算和稳定性评价。邓超等[9]采用不同赋值的全参数输入模型( FOS-ELM-M7) 建立边坡参数反演模型，为获取岩体边坡参数提供了一种快捷的新方法。闵江涛等[10]将遗传算法(GA)与神经网络算法(BP)相结合，建立基于改进的GA-BP网络算法反分析模型，经过网络训练，得到符合实测效应量值的反演参数值。

反演法根据边坡的稳定状态选取临界稳定系数对岩土体强度参数进行反算，再根据反算结果对边坡进行加固设计，此法弥补了试验方法的不足之处，经过学者近年的研究、改进，在工程应用中取得了良好效果[11-12]。本文研究区边坡为二元结构的顺向坡，第一次边坡治理时采用毕肖普法进行边坡稳定性计算，实施后部分区域仍有较大变形。为探究第一次滑坡治理失败的原因，采用基于Morgenstern-Price法的极限平衡理论，建立力学模型，通过河海大学开发的Autobank软件进行数值模拟反演分析，为边坡第二次治理提供依据。

1 研究区滑坡基本特征

某大坝为面板砂砾石堆石坝、溢洪道布置在左岸，地形地貌为左岸河床至正常蓄水位790 m高程以下附近为缓坡，坡度13°～17°，高程845 m坡度约30°；高程845 m至高程855 m左右为缓坡山腰平台，坡度小于10°，宽度约50 m。平台高程855 m以上坡度大于30°，左岸山顶高程大于900 m。揭露覆盖层主要为含碎石(块石)黏性土，直接覆盖在弱风化岩体之上，中间缺乏残积层和全风化层，覆盖层厚约5.3～15.0 m；下伏基岩为三叠系中统边阳组第二段(T2b2)青灰色中至厚层状(粉)细砂岩夹泥页岩。

施工时对溢洪道进口控制段上部边坡开挖，覆盖层采用1.00∶1.25坡比多级开挖，每级坡高10 m，马道宽2 m；一二级边坡开挖后，边坡850 m高程平台前侧出现宽1 m以上的裂缝，后该区域又发生24 h内160 mm的强降雨，导致大面积滑坡，并形成泥石流进入河道。滑坡体如舌形展布，最大宽度约390 m，滑坡后缘至滑舌底部最大高差142 m；滑坡情况见图1，其平面见图2。该区滑坡后使地质结构露头，地质认识逐渐清晰，岩层产状走向55°～70°/倾向NW∠倾角25°～35°，整个坝址左岸山体与岩体构成顺向坡；为上部松散覆盖层下伏弱风化岩板的二元结构顺向边坡。

图1 溢洪道进口控制段边坡滑坡照片

图2 溢洪道边坡及监测仪器平面布置

2 泄槽段边坡第一次加固后稳定性分析

2013年11月在对溢洪道进口段及复建公路边坡开挖过程中，左侧上方山体850.0 m处出现1～2 m的错动裂缝，将覆盖层边坡放缓后继续开挖。2014年6月20日，施工时发生特大暴雨(降雨量达160 mm)，导致溢洪道边坡发生大面积滑坡，后将溢洪道进口控制段边坡覆盖层清理至弱风化岩板，并对岩板进行锚喷支护，该段边坡2015年10月治理完成后基本稳定。同时对溢洪道泄槽段边坡进行普通抗滑桩加固，桩径1.5 m，间距3 m，设计抗力760 kN/m，抗滑桩顶部采用钢筋混凝土冠梁连接，抗滑桩及冠梁施工于2015年10月完成。2015年11月，溢洪道泄槽段开挖过程中，上部山体覆盖层再次发生位移，桩顶冠梁亦多处开裂。因此，本文主要以泄槽段边坡为研究对象，对其稳定性进行计算并分析再次发生位移原因，溢洪道泄槽段第一次治理典型剖面见图3。

图3 溢洪道泄槽段边坡加固典型剖面

2.1 稳定性计算

选取溢洪道泄槽段典型剖面图建立力学模型，采用简化毕肖普法的极限平衡理论，利用河海大学开发的Autobank稳定、渗流软件进行稳定性计算，力学参数为现场取样室内试样获得，室内试验值见表1。计算工况为正常工况、降雨工况、地震工况3种，正常工况为天然状态下的边坡稳定状态，选取天然状态下的力学参数计算；降雨工况为边坡在降雨条件下的稳定状态，取上部碎石土饱和状态、下部粉质黏土及弱风化砂岩在饱和状态下的力学参数计算。研究区地震动峰值加速度为0.1 g，地震动反应谱特征周期为0.35 s，相应地震基本烈度Ⅶ度，地震工况下重力加速度取0.1 g参与计算，力学参数为天然状态下的力学参数。计算模型上部为碎石土，中部为粉质黏土，下部为弱风化粉砂质泥岩，计算时选取各工况下对应的力学参数进行计算，计算结果见表2。本边坡为4级边坡，按照SL 386—2016《水利水电工程边坡设计规范》[13]取允许值列于表2，利用Autobank软件计算的第一次加固处理后边坡稳定系数见图4。

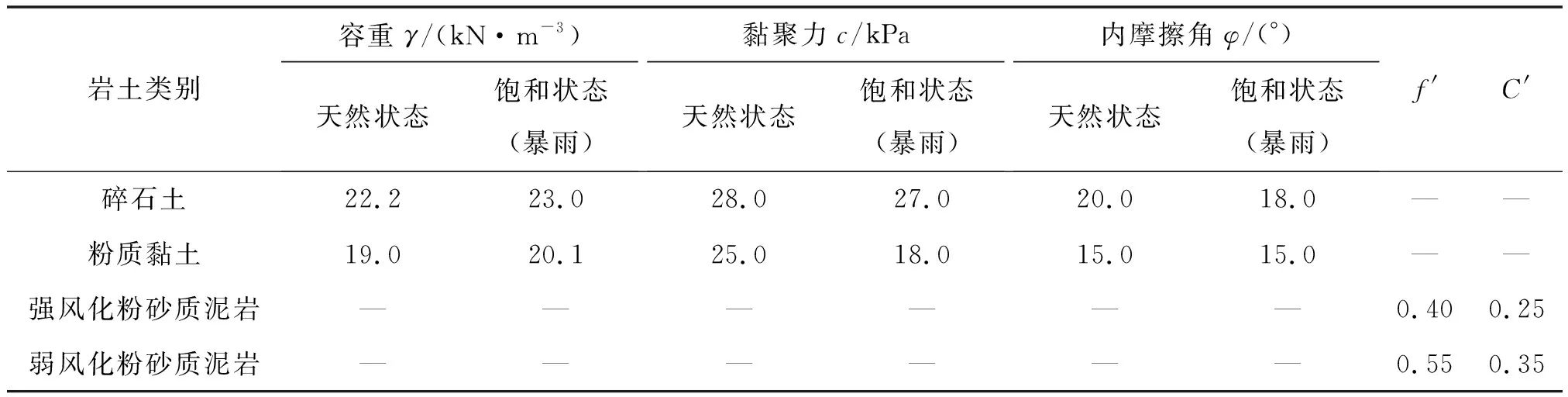
表1 研究区滑坡体岩土体主要物理力学参数试验值

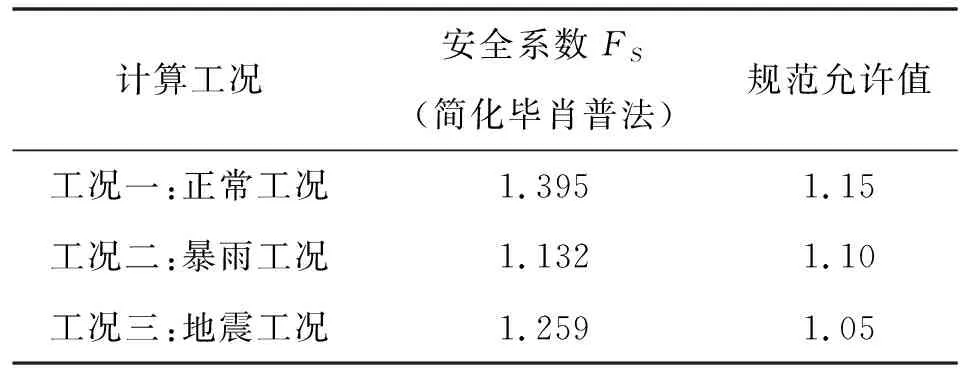
表2 滑坡体第一次加固后安全系数计算结果

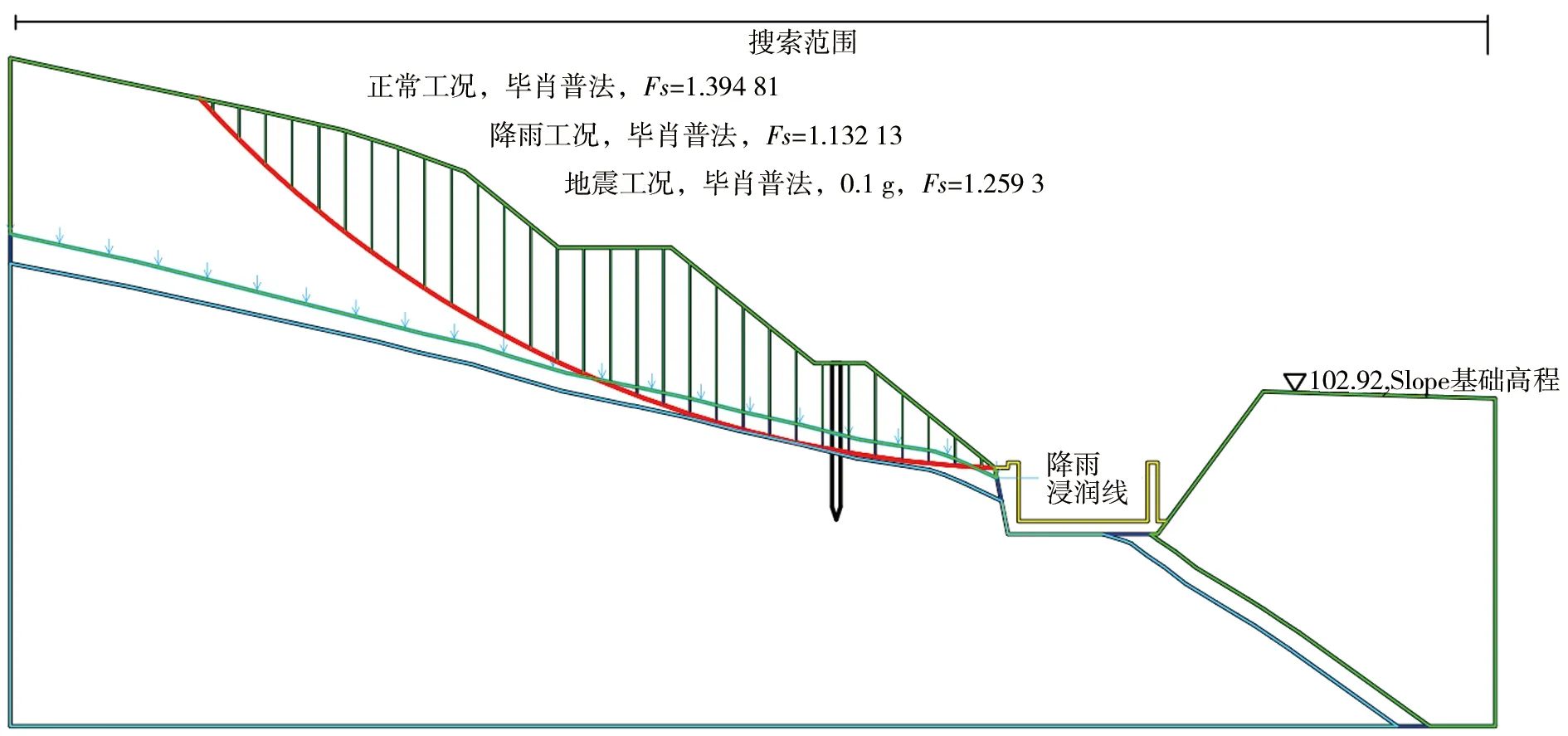
图4 第一次加固处理后边坡计算结果

2.2 失稳原因分析

由表2及图4第一次加固边坡稳定性计算结果可知，正常工况、暴雨工况、地震工况3种情况下计算结果均满足规范允许安全系数要求，表明该边坡处于稳定状态，此结果与现场实际出现较大变形裂缝不符(现场抗滑桩冠梁多处裂缝见图5)，表明该计算结果存在偏差。

图5 现场抗滑桩冠梁裂缝

加固后仍出现较大变形的原因是溢洪道槽底土体切角开挖，形成临空面，加之开挖时雨水较多等；边坡在降雨条件下发生较大裂缝，说明降雨工况下边坡处于不稳定状态。黏聚力c和内摩擦角φ的取值对是否安全和经济有重要影响，取值过大，可能产生滑坡；取值过小，会造成设计浪费。因此分析认为第一次加固计算时，采用的简化毕肖普法的极限平衡理论适用于覆盖层剪切破坏，实际滑坡为覆盖层沿岩板滑动破坏，故力学模型选取有误。其次，因选取的饱和状态的力学参数偏大，导致第一次加固设计计算的降雨工况下的安全系数偏大。通过对岩土体降雨工况时的力学参数进行反演分析，得出降雨时最优的物理力学参数，以该参数为参考对研究区边坡进行第二次加固设计。

3 滑坡体力学参数反演分析

3.1 计算方法

沿堆积物底面基岩顶板发生滑动破坏时，宜采用不规则滑面计算，一般用下限解法求解稳定系数，如Morgenstern-Price法、Janbu法和传递系数法分析计算。本文采用Morgenstern-Price法进行分析计算，该法的力学平衡条件为分条底面的法向力平衡、分条底面的切向力平衡和对于分条底面中点的力矩平衡。其假设条块的竖直切向力与水平推力之比为条间力函数f(x)与待定常数λ的乘积，Morgenstern-Price法的计算模型见图6。

3.2 模型建立

首先根据第一次加固方案，选取溢洪道泄槽段边坡3个断面进行稳定性计算，从中选出安全系数最小的断面为最危险断面，作为敏感性分析及参数反演的计算模型，利用Autobank软件建立计算模型。

对于均质边坡，降雨的影响主要在湿润峰以上，对下层孔隙水压力影响微弱；当边坡存在贯穿裂隙时，暴雨才容易引起深层滑坡[14]。研究区二元结构边坡覆盖层较厚(约5.3～15.0 m)，下伏基岩为细砂岩夹泥页岩，且边坡岩体不存在贯穿裂隙，可认为降雨对下层岩体的力学参数影响微弱。同时室内试验发现，饱和状态下细砂岩的物理力学性质变化较小。另外经分析计算发现，研究区边坡最危险滑坡面主要集中在碎石土与基岩接触面，下伏基岩的物理力学性质对边坡稳定性的影响不大。因此在分析计算时认为降雨仅对碎石土的物理力学参数产生影响，下伏砂岩的物理力学参数保持不变。故本文将研究降雨工况下上部碎石土黏聚力c和内摩擦角φ对安全系数的影响，利用敏感性变化关系，反演上部碎石土降雨工况时的最优力学参数，为二次滑坡治理提供依据。

3.3 敏感性分析

对研究区边坡安全系数进行敏感性分析时，假定2种计算情况：①黏聚力c按试验值保持不变，改变内摩擦角φ的大小，计算安全系数；②保持内摩擦角φ不变，改变黏聚力c的值，计算安全系数。根据二者计算结果分析安全系数与内摩擦角φ和黏聚力c的敏感性变化关系，计算结果见表3、4。

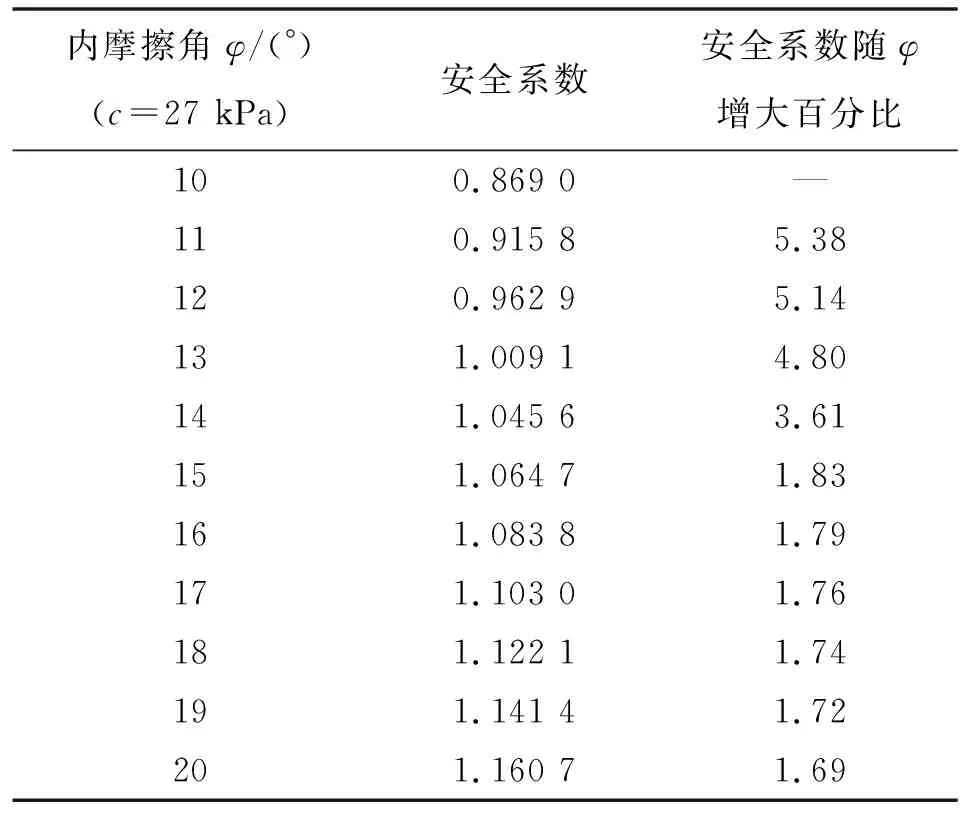
表3 安全系数对内摩擦角φ的敏感性分析

表4 安全系数对黏聚力c的敏感性分析

由以上计算结果可知，安全系数随内摩擦角的增加而增大，但随着内摩擦角的增加，安全系数增大的敏感性降低。安全系数随黏聚力的增加而增大，且安全系数与黏聚力的关系基本呈线性关系。比较安全系数百分比增幅可知，内摩擦角每增加1°，安全系数平均增大3.36%；而黏聚力每增加1 kPa，安全系数平均增涨0.75%。由此说明降雨入渗于土体中，对内摩擦角和黏聚力均有一定程度的影响，使得该参数同时降低，但安全系数对内摩擦角φ的敏感度更高。

3.4 反演参数确定

根据滑坡现场勘察结果和滑坡变形特点分析，研究区滑坡在正常工况下保持稳定，而在降雨工况下发生裂缝变形，参考表5的变形特点，取降雨工况下的安全系数为1.00，对该研究区滑坡体在饱和状态下的物理力学参数进行反演，选取最优力学参数。

表5 不同滑坡变形下的稳定取值

由4.3小节可知，边坡稳定对内摩擦角φ的敏感性比对黏聚力c的敏感性更强，因此选取一组单向递增数据，在c=18、19、20、21、22、23、24 kPa共7组数据下，反演内摩擦角φ的大小，使得边坡的安全系数等于1.00。影响边坡稳定的力学参数主要是c和φ值，2个未知数需要2个方程才能求解，因此选取2个断面采用上述同样的方法进行反演计算分析，计算成果见表6。

表6 碎石土力学参数反演计算值

将以上2个断面的反演计算结果绘于图7中，可以发现通过2个断面反演计算求出的曲线相交于一点，求出该点的坐标为c=21.5 kPa，φ=14.5°，该值即为通过反演方法所求出的碎石土在饱和状态下的力学参数。需要说明的是，在反演计算过程中，若选取3个或以上断面时，可能出现交点不唯一、或出现两条平行线导致无交点情况，此时应校核滑坡的稳定状态或初始条件，重新选定初始条件后进行分析，直到所求结果满足反演指标要求为止[15]。

图7 通过反演计算求出的2种断面c、φ参数曲线

3.5 治理设计与治理效果

根据反演分析计算得出的力学参数进行第二次加固设计，第二次加固设计措施为：上部新增一排抗滑桩，桩径2.5 m，间距5 m，设计抗力1 200 kN/m。同时采用预应力锚索加固，锚索深入基岩15 m，锚索预应力1 000 kN；对已有下部抗滑桩进行加固处理，第二次加固新增锚索抗滑桩布置见图8。

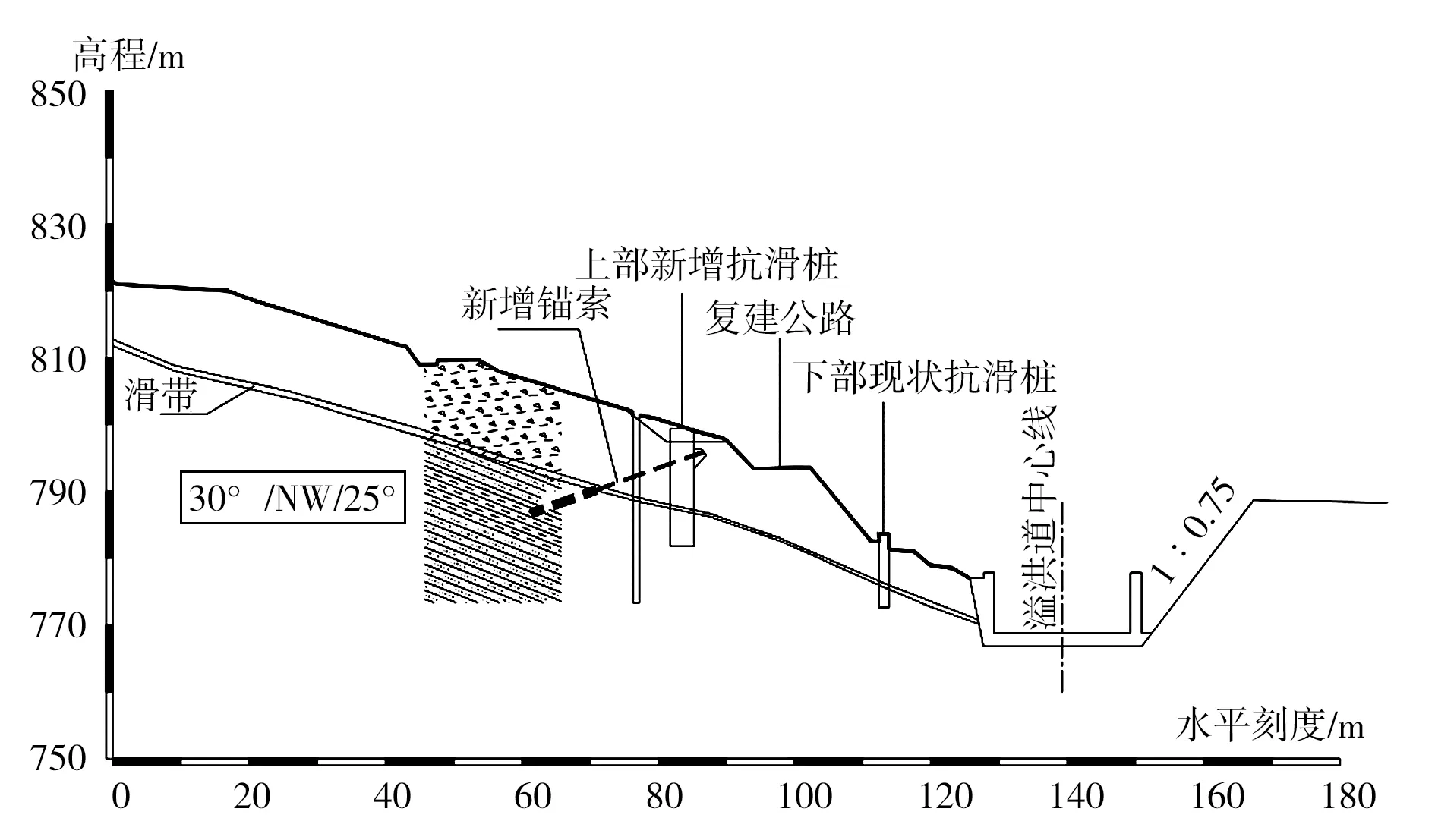
图8 第二次加固典型横断面

确定第二次加固方案后，根据反演参数对第二次治理设计进行边坡稳定性计算，计算二次加固后的安全系数见表7。

由表7计算结果可知，在正常工况、暴雨工况和地震工况条件下，基于反演参数计算的边坡第二次加固后的稳定系数均符合规范要求。对该边坡进行外部变形监测，滑坡体变形监测点布置见图2，地表监测位移结果见图9。监测数据显示，滑坡体在2015年11月出现裂缝后，2016年5月底在降雨影响下，边坡又出现较大变形。而在2016年7月随着第二次加固措施的实施，桩顶冠梁及边坡变形开始收敛，并逐步稳定。截至目前，该研究区已持续观测多年，数据显示滑坡体无新增裂缝、无明显位移。安全系数计算结果和位移监测结果说明，第二次加固的措施安全可行，按照此反演法得出的力学参数值可靠。

表7 第二次加固后的边坡安全系数

a)水平位移

4 结论

本文对研究区滑坡体第一次加固失效的原因进行探讨，利用Autobank软件对该滑坡体稳定性进行敏感性分析，探究黏聚力c和内摩擦角φ对安全系数的影响。基于敏感性变化关系，反演岩土体力学指标，采用该反演参数对滑坡体进行二次加固设计。经研究分析，得出如下结论。

a)二元结构边坡在覆盖层沿底面基岩顶板发生滑动破坏时，宜采用不规则滑面计算，一般用下限解法求解稳定系数，如Morgenstern-Price法适用性较强。

b)土体抗剪强度参数对边坡稳定有重要影响，特别是降雨条件饱和状态下，力学参数的选取对边坡的稳定性计算至关重要；若选取不当，可能导致边坡产生裂缝变形甚至滑坡失稳。

c)安全系数随内摩擦角的增加而增大，但随着内摩擦角的增加，安全系数的增大幅度降低。安全系数随黏聚力的增加也增大，且安全系数与黏聚力的关系基本呈线性关系。与黏聚力c相比较，安全系数对内摩擦角φ的敏感性更强。

d)计算及监测结果说明，第二次边坡治理措施安全可行，利用反演参数求出的饱和状态下的力学参数可靠，此反演分析法可为其他类似工程提供一定借鉴。