中国男性人口死亡率动态预测的方法比较——基于Lee-Carter模型与贝叶斯分层模型的研究

赵明

(首都经济贸易大学 金融学院，北京 100070)

1 引言与文献综述

随着社会经济的发展和医疗水平的提升，人口寿命延长已成为不可逆转的趋势。人口寿命延长导致的人口年龄结构变化，将会对社会经济产生较大的负面影响。合理地预测人口死亡率、掌握人口年龄结构随时间变动的趋势、提前采取应对措施，将会有效减缓长寿风险对经济的冲击。因此，人口死亡率预测将成为一个基础且重要的研究课题。人口死亡率预测的常用方法包括两种：一是先预测分年龄死亡率，再通过分年龄死亡率计算人口预期寿命；二是先预测人口预期寿命，然后通过既定的模型生命表计算分年龄死亡率。

对于人口死亡率预测的国内外研究较早，其中Lee-Carter模型开创了随机死亡率建模的先河[1]。Lee-Carter模型假设对数死亡率由相互独立的年龄效应和周期效应构成，具有模型参数少、拟合过程简单和预测结果稳健等优势，得到学者的普遍应用[2]。Lee-Carter模型采用两阶段方法进行参数估计与拟合，第一阶段通常使用奇异值分解(SVD)或最大似然(ML)方法估计静态参数；第二阶段通过时间序列模型(ARIMA模型)拟合动态参数[3]。随着该理论与应用的不断发展，Lee-Carter模型也暴露出一定缺陷，其改进主要包括以下几方面：一是参数估计方法的改进。Lee-Carter模型参数估计的奇异值分解(SVD)方法误差较大，采用加权最小二乘估计(WLS)方法和极大似然(ML)方法能够有效提高参数估计的拟合优度。此外，样本数据时间周期的选取对Lee-Carter模型参数估计与预测结果产生显著影响，为了在死亡率不规则的情况下提高Lee-Carter模型的精确度，应采用科学方法选取历史数据周期。二是放宽模型假设。针对Lee-Carter模型中假设过强的问题，部分学者提出了泊松对数双线性(PB)模型，假设死亡人数服从泊松分布，放宽了模型残差项同方差的假设[4]。在死亡人数服从泊松分布的假设下，构造泊松似然函数，采用贝叶斯方法对模型参数进行估计[5]。三是有限数据问题下的方法改进。Lee-Carter模型对数据连续性具有较高要求，限制了该方法在有限数据国家的应用。Li等(2004)在对数双线性假设下提出了基于有限数据的Lee-Carter模型方法，能够有效解决数据较少国家死亡率预测问题[6]。此外，我国学者也采用有限数据下Lee-Carter模型对中国人口死亡率进行预测，在样本量较少时，对时间序列的波动性进行研究，使得预测结果更加稳健与合理[7]。四是死亡率改善因子动态改进。Lee-Carter模型中常数人口死亡率改善因子假设被多位学者认为并不合理，如果建模时不考虑死亡率改善因子随时间进展的变化，则长期预测会出现严重偏误，尤其是对于死亡率改善程度较低的国家[8]。为了避免这种情况，在Lee-Carter模型中加入了一个旋转项，来体现人口死亡率改善随时间的变动趋势，并通过使新加项随时间连续地发生旋转来改进Lee-Carter模型中常数死亡率改善因子的假设[9]。此外，采用双因子Lee-Carter模型，基于贝叶斯MCMC方法，改进单因子Lee-Carter模型中死亡率改善为常数的假设，可以显著提升模型拟合优度[10]。

此外，以人口预期寿命为建模对象的方法，在联合国预测人口死亡率时较为常用。Girosi和King(2008)选取48个国家的男性人口死亡率，并选取人口吸烟情况和国内生产总值作为协变量，采用贝叶斯模型方法在年龄和时间两个维度对人口死亡率进行预测。然而，Girosi和King(2008)的方法对数据要求较高，需要选取特定的协变量才能得到较好的预测效果，在模型扩展方面具有一定的局限性。Raftery等(2013)提出了基于贝叶斯分层模型(BHM)的人口死亡率预测方法，将世界各国1950～1995年预期寿命数据带入贝叶斯分层模型，对1996～2005年各国的预期寿命进行预测，通过与实际数据交叉检验，认为模型能够给出精确的预测区间[11]。此后，在Raftery等(2013)的基础上，部分学者对该方法进行了实践与扩展，但应用主要都集中在人口统计方面，在其他领域的应用较少。Li等(2015)对人口死亡率改善因子建模，将相关国家的死亡率改善趋势作为先验信息，给出了贝叶斯分层模型下死亡率的动态预测方法，并运用1991～2011年英国和丹麦女性人口死亡率进行验证，得到了较好的预测结果[12]。Les和David(2015)提出了一种基于分解技术(decomposition techniques)的期望寿命预测方法，考虑不同年龄人群死亡率改善程度的差异，对预期寿命建立贝叶斯分层模型，模型设计更具有针对性[13]。贝叶斯分层模型能够有效应对世界各国人口死亡率数据质量参差不齐的情况，使用具有非恒定漂移的随机游走模型预测人口预期寿命，并将数据质量较好的国家人口预期寿命的改善趋势作为先验信息，较好地弥补了数据质量较差国家自身数据不足的缺陷。贝叶斯分层模型方法被联合国人口司所采用，该机构每两年发布一次《世界人口展望》研究报告。根据联合国人口司的研究表明，不同国家人口预期寿命的增长速度不同，低寿命国家和高寿命国家的预期寿命的增长较慢，而中等寿命国家的预期寿命增长较快。

综上所述，Lee-Carter模型方法的研究对象为人口死亡率、贝叶斯分层模型方法的研究对象为预期寿命，当前两种研究方法均具有较为成熟的范式，但从生命表的构造理论上看，分年龄死亡率和预期寿命之间具有密切的联系，如果将两者之间的相互关系考虑进来，可以比较分析两种方法下中国男性人口死亡率预测的差异，提升死亡率预测质量。本文从比较的视角来评估两种方法下男性人口死亡率的预测结果，并根据生命表构造理论将两者相互转换，通过对模型结果进行比较分析，一方面可以检验预测结果的准确性，另一方面还能作为研究结论相互补充。通过本研究，以期能够提升中国人口死亡率预测和长寿风险度量的可靠性，合理预判未来人口年龄结构变动趋势，为国家制定退休方案、生育政策和积极应对人口老龄化等重大决策提供科学依据。

2 人口死亡率预测方法概述

2.1 Lee-Carter模型

Lee-Carter模型的表达式为

lnmx,t=αx+βxκt+εx,t

(1)

其中，mx为中心死亡率，而通过贝叶斯分层模型和模型生命表法得到的是死亡概率qx。由于我国统计局公布的抽样调查年份死亡率数据是以年中人口数为分母计算得到的中心死亡率，在死亡均匀分布(UDD)假设下二者具有如下转换关系：

qx=2mx/(mx+2)

(2)

对于Lee-Carter模型其他参数的介绍，本文不再赘述，具体可参见Lee和Carter(1992)的研究。由于Lee-Carter模型对历史数据要求较高，本文采用1994～2012年人口死亡率数据进行预测，则第一个预测年为2013年。本文采用Wilmoth(1996)提出的加权最小二乘法[14]对Lee-Carter模型进行参数估计，采用ARIMA(0,1,0)模型对时间效应因子κt进行预测。

2.2 贝叶斯分层模型

贝叶斯分层模型以预期寿命为研究对象，是一个带有非恒定漂移项的随机游走模型，表达式为

lc,t+1=lc,t+g(lc,t)+εc,t+1

(3)

其中，lc,t表示国家c在t时期的预期寿命，lc,t+1表示国家c在t+1时期的预期寿命，它是用lc,t加上一个预期寿命增量g(lc,t)和一个随机扰动项来表示的。漂移项是当前预期寿命的非线性函数，它能够反映不同国家在不同寿命水平下预期寿命的增长速度，Raftery等(2013)使用一个Double-Logistic函数来表示这个增量。此外，随机扰动项的标准差与上一期预期寿命呈现出的关系可用下式加以描述：

εc,t+1～N[0,(w×f(lc,t)2)]

(4)

贝叶斯分层模型包含13个参数，每个参数均有一个先验分布，可使用马尔科夫链蒙特卡洛随机模拟方法(以下简称“MCMC方法”)估计每个国家预期寿命后验分布的参数。相比于Lee-Carter模型对数据质量的要求较高，贝叶斯分层模型适用于数据质量各异的国家。

2.3 人口死亡率修匀模型

中国国家统计局公布的人口死亡率数据是未经修匀和调整的粗死亡率数据、波动较大，应采用适当的方法对数据进行修匀。由于本文拟对人口死亡率进行动态预测，死亡率不仅具有年龄上的分布规律，同时在时间上也具有特定的分布规律，因此本文选用二维修匀方法对动态生命表进行修匀[15][16]。常用的两种非参数二维修匀方法为二维泊松P-样条模型和二维离散Beta核修匀模型，在对中国人口死亡率动态生命进行修匀时，尽管二维离散Beta核修匀模型在全年龄段上的拟合度更优，但光滑性较差，尤其是对边端年龄处理效果不佳，使修匀后的新生婴儿死亡率与实际情况出现较大的偏差[17]。综上，本文选择二维泊松P-样条模型对粗人口死亡率进行修匀，具体计算过程详见Mazza和Punzo(2013)的研究。

2.4 人口死亡率与预期寿命的转化

根据生命构造理论，当死亡分布为连续函数时，人口死亡率与预期寿命之间的关系为

(5)

由于本文所采用的人口死亡率为离散型年度数据，对上式离散化为

(6)

本文采用上式将人口分年龄死亡率转化为预期寿命。此外，将人口预期寿命转化为分年龄死亡率，本文选用联合国模型生命表方法。联合国人口司(1982)编制了一套发展中国家模型生命表，其数据源自于22个发展中国家的72张生命表(男、女性生命表各36张)，并经过严格检验，具有较可靠的质量。这套模型生命表根据实际数据所反映的死亡率模式的地域特征分为几大区域，分别定名为“拉丁美洲”表、“智利”表、“南亚”表、“远东”表和“通用”表。其中，“通用”表根据全部国家数据编制，能够代表发展中国家的一般情况。

2.5 模型误差分析

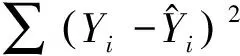
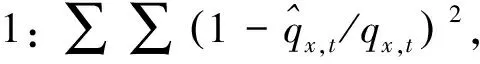
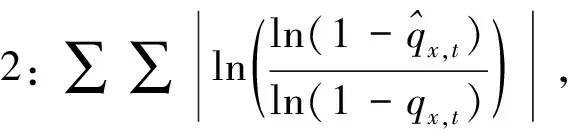
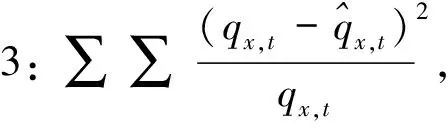
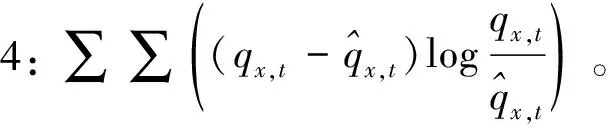
其中，t表示年份，x表示年龄。以上4个误差函数分别采用相对值、绝对值、平方值和对数值等一种或多种方法组合，构造了拟合值与实际值之间差异的误差函数。在对死亡率模型拟合优度进行评价时，同时使用4个误差函数能够更加稳健地评价模型的拟合效果。

3 数据处理与实证分析

3.1 数据处理与假设

本文选取全国男性人口死亡率数据，其数据来源于1995～2006年的《中国人口统计年鉴》，以及2007～2020年的《中国人口和就业统计年鉴》。本文将数据分为两组，分别为预测组和对照组。预测组所采取用的数据为全国男性人口分年龄的死亡率数据，数据期间为1994～2012年，共计19年。其中，2000与2010年的死亡率数据来自人口普查，1995与2005年的数据为来自1%的抽样调查，其他年份的数据来自于人口变动抽样。对照组选取2013～2019年数据，用以检验Lee-Carter模型和贝叶斯分层模型的预测效果。

根据本文所选取数据的特征与实证分析的需要，具体的数据处理与假设如下：

第一，选取男性人口为代表进行研究。中国国家统计局公布的抽样调查数据中，部分年龄死亡人口数为0，导致死亡率数据失真。由于女性人口死亡率低于男性，这种失真现象在女性人口中更为普遍，因此男性人口死亡率具有更好的数据质量。当男性人口抽样调查中死亡人数为0或者缺失时，采用线性插值方法进行填补。

第二，修正婴儿人口死亡率数据。由于人口普查中死亡数据在低龄和高龄期存在不同程度漏报[19]，尤其是新生婴儿死亡数据漏报更为严重。本文借鉴人口学界的相关研究，对新生婴儿死亡率数据做出修正，并在修正的基础上进行死亡率修匀。已有研究显示，第五次人口普查中低龄组漏报率约10%，且女童漏报大于男童，男女婴儿死亡率修改后分别为31.35‰和23.89‰[20]；第六次人口普查中婴儿漏报率为78%～85%，修正得男婴死亡率25.81‰，女婴死亡率17.82‰[21]。此外，针对其他年龄的死亡率数据，本文采用二维P样条方法进行修匀，以使粗死亡率更加符合生命表特征。

第三，重新调整各年份死亡人口数。由于我国人口死亡数据中包括普查与抽样调查不同方式的数据，在采用加权最小二乘方法求解Lee-Carter模型时，需要用到量级相同的死亡人口数。本文根据调整并修匀后的分年龄人口死亡率数据，以100万数量的人口为基准，对各年龄的死亡人数进行调整。

第四，假设85岁以上人口为高龄人口。由于高龄人口数据少，可信度低，本文将人口年龄段截止到85岁，不再探讨高龄人口死亡率建模问题。

第五，假设死亡人口在1年内服从均匀分布(UDD)假设。

3.2 基于Lee-Carter模型的预测结果

采用Lee-Carter模型，可以得到2013～2050年中国男性人口的分年龄死亡率，结果列示于表1中。

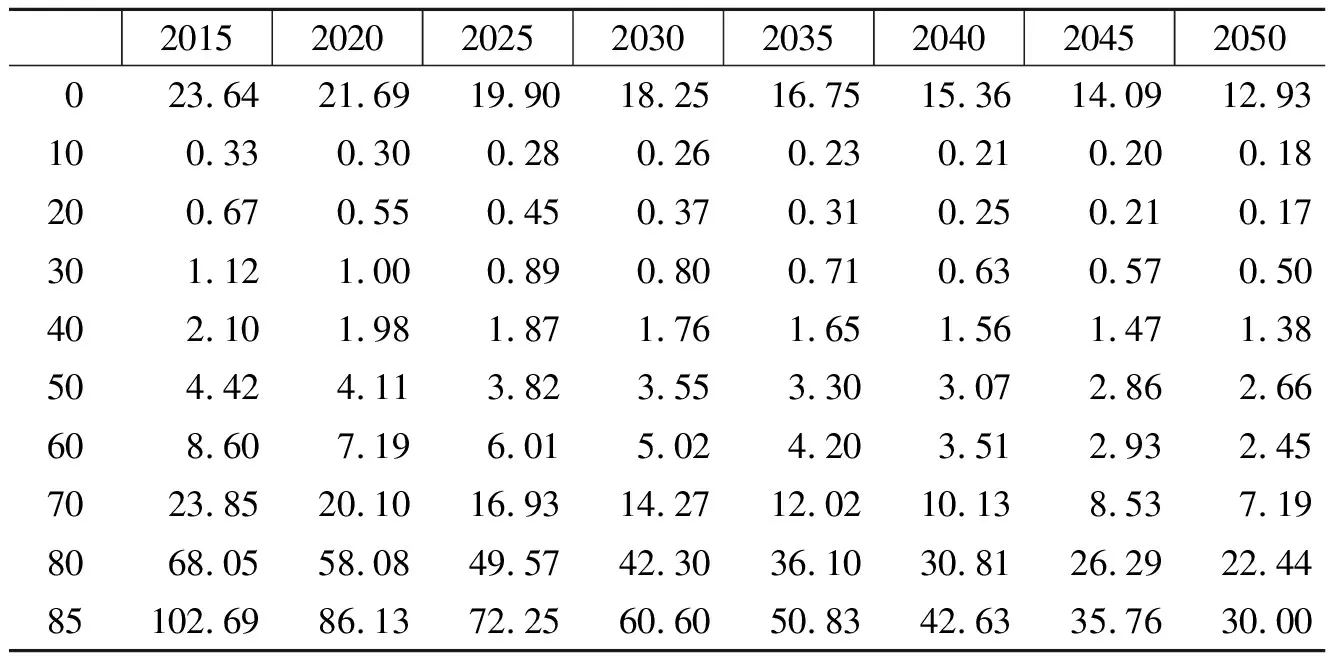
表1 基于Lee-Carter模型的中国男性人口死亡率预测值(单位：‰)

由表1可见，Lee-Carter模型得到的预测值，能够很好地反映男性人口死亡率随时间、年龄变动的趋势。从时间维度看，新生男婴死亡率由2015年的23.64‰，下降到2030年的18.25‰，再下降到2050年的12.93‰，整个35年的下降幅度为45.30%；30岁男性人口死亡率由2015年的1.12‰，下降到2030年的0.80‰，再下降到2050年的0.50‰，整个35年的下降幅度为55.36%；85岁男性人口死亡率由2015年的102.69‰，下降到2030年的60.60‰，再下降到2050年的30.00‰，整个35年的下降幅度为70.79%。综上可见，未来中国男性人口死亡率下降的幅度，随着年龄增长而不断提升，低年龄人口死亡率改善不断充分，下降幅度减小，而中高龄人口死亡率改善速度逐渐提高，体现出了死亡率变动的年龄模式特征。此外，Lee-Carter模型假设人口死亡率在时间上的下降速度为常数，即假设未来人口死亡率的下降速度仍保持历史水平不变。自改革开放以来，中国人口死亡率一直以较快速度下降，但未来是否能够持续这一趋势值得商榷，但Lee-Carter模型中并未考虑到这个问题。若未来人口死亡率改善减速，那么运用Lee-Carter模型进行长期预测将会低估死亡率、高估人口预期寿命。

进一步，根据生命表构造理论，将Lee-Carter模型预测的男性人口死亡率转换为预期寿命值，结果列示于表2中。在表2中，给出了高、中、低三个假设下男性人口预期寿命的预测值。其中，居中假设为均值估计结果，高假设和低假设分别为预期寿命80%置信区间的上下界。在居中假设下，2015年人口预期寿命为73.63岁，到2030年提高到77.10岁，到2050年提高到80.36岁，整个35年提高了6.73岁，平均每10年提高1.92岁，但提高速度随时间推移而递减。尽管Lee-Carter模型预测的男性人口死亡率下降速度是常数，但男性人口平均寿命提高速度在减缓，其原因是不同年龄人口死亡率下降速度不同，导致人口年龄结构发生变化，即分年龄死亡率与人口预期寿命之前并非简单的线性关系。由于Lee-Carter模型以分年龄死亡率为研究对象，可以获取到较为丰富的人口死亡率信息，在此基础上进一步计算人口预期寿命，可以更好地分析二者间的关系及人口年龄结构变动的影响。此外，Lee-Carter模型得到的男性人口预期寿命预测区间的幅度较窄，2015～2050年每隔5年的80%置信区间上下界预测结果差值分别为0.14岁、0.13岁、0.12岁、0.11岁、0.10岁、0.09岁、0.08岁和0.08岁。甚至，随着时间推移，Lee-Carter模型获得的男性人口死亡率预测区间会进一步收窄，从长期预测的角度来看，这种预测结果并不理想。

表2 基于Lee-Carter模型的中国男性人口预期寿命预测值 (岁)

表3 基于贝叶斯分层模型的中国男性人口预期寿命预测值 (岁)

3.3 基于贝叶斯分层模型的预测结果

采用贝叶斯分层模型，对中国男性人口预期寿命做出预测，预测结果列示于表3。在表3中，给出了高、中、低三个假设下人口预期寿命的预测值。其中，居中假设为均值估计结果，高假设和低假设分别为预期寿命80%置信区间的上下界。由表3可见，在居中假设下，2015年人口预期寿命为74.39岁，到2030年提高到76.51岁，到2050年提高到78.96岁，整个35年提高了4.57岁，平均每10年提高1.31岁，寿命提高速度显著低于Lee-Carter模型估计结果。由于Lee-Carter模型中假设了死亡率下降速度为常数，按照历史死亡率下降速度来预测未来；从贝叶斯分层模型的预测结果中可以看到，在长期中人口预期寿命预测值低于Lee-Carter模型结果，是由其模型假设决定的。贝叶斯分层模型采用了双逻辑斯蒂假设，即假设人口预期寿命的增长速度呈现先快、后慢的S型曲线分布。因此，基于贝叶斯分层模型的人口预期寿命的预测值，在2025年以前整体上高于Lee-Carter模型预测结果，而2025年以后则低于Lee-Carter模型预测结果。此外，贝叶斯分层模型得到的男性人口预期寿命预测值，具有相对较宽的预测区间，2015～2050年每隔5年的80%的置信区间的上下界预测结果差值分别为3.17岁、4.39岁、5.48岁、6.47岁、7.38岁、8.15岁、8.72岁和9.17岁。随时间推移，贝叶斯分层模型获得的死亡率预测区间会进一步增大。从长期预测的角度来看，这种预测结果较为理想。

通过对比不同模型生命表与我国2010年人口普查的分年龄男性人口死亡率的关系，认为“通用”表更适合我国实际死亡状况。因此，选取联合国人口司模型生命表中的“通用”表，将贝叶斯分层模型预测的男性人口预期寿命转化为分年龄死亡率,结果列示在表4中。

由表4可见，基于贝叶斯分层模型和“通用”模型生命表得到的未来中国男性人口死亡率预测值，能够很好地反映死亡率随时间、年龄变动的趋势。从时间维度看，新生男婴死亡率由2015年的21.83‰，下降到2030年的17.63‰，再下降到2050年的13.83‰，整个35年的下降幅度为36.65%；30岁男性人口死亡率由2015年的0.71‰，下降到2030年的0.55‰，再下降到2050年的0.42‰，整个35年的下降幅度为40.85%；85岁男性人口死亡率由2015年的117.40‰，下降到2030年的105.68‰，再下降到2050年的91.12‰，整个35年的下降幅度为22.39%。综上可见，未来男性人口死亡率下降的幅度，随着年龄增长呈现先提高、再降低的趋势，即低龄和高龄男性人口死亡率改善速度较低，而中年男性人口死亡率改善速度较快。由于贝叶斯分层模型是以人口预期寿命为研究对象，预测得到的人口预期寿命需要通过既定的模型生命表转化为分年龄死亡率，因此会损失死亡率在年龄上展现出的更为丰富的信息。但长期中，贝叶斯分层模型能够得到更宽的预测区间，预测结果的稳健性较好。

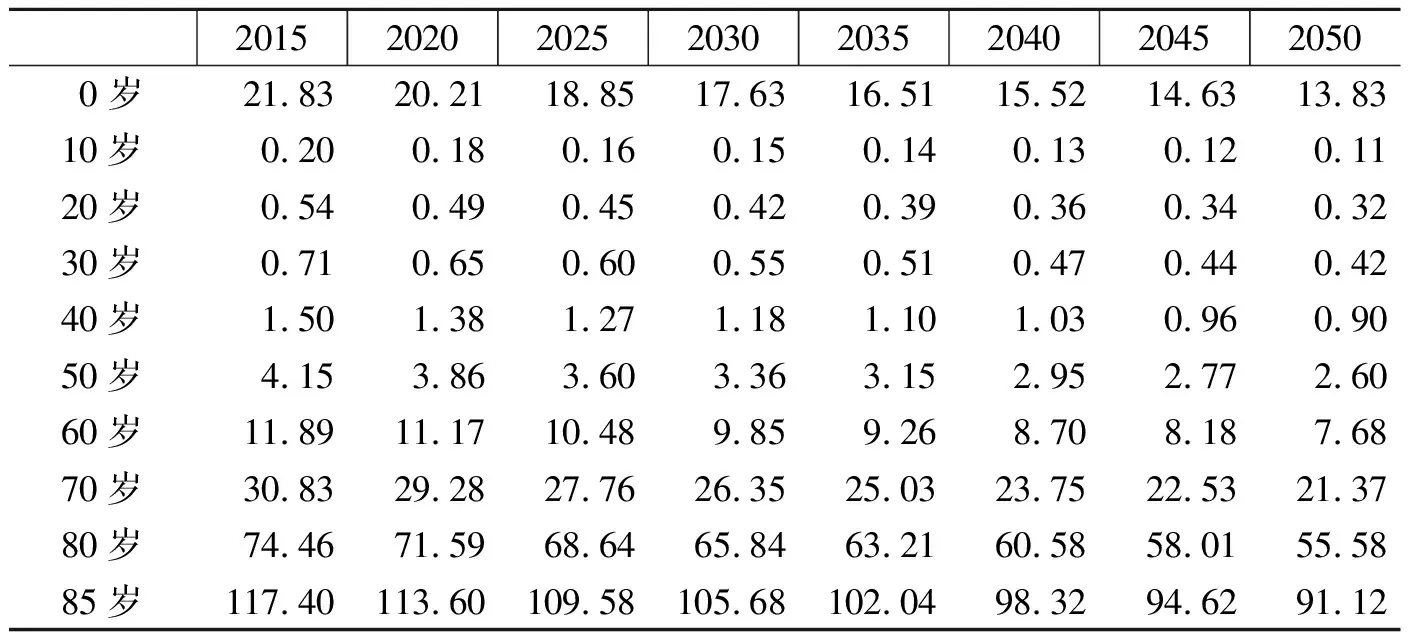
表4 基于贝叶斯分层模型的中国男性人口死亡率预测值 (‰)

表5 两种方法下中国男性人口死亡率拟合结果误差比较

表6 两种方法下中国男性人口死亡率短期预测效果比较

3.4 两种模型下预测结果比较与评价

3.4.1 样本内的拟合优度比较

本文分别采用四种损失函数对两种模型方法的样本内拟合情况进行检验，结果列示于表5中。

由表5可见，基于调整和修匀后的人口死亡率数据，采用Lee-Carter模型进行拟合，在四种误差函数下误差值均小于贝叶斯分层模型，即Lee-Carter模型的拟合优度高于贝叶斯分层模型。意味着，Lee-Carter模型简洁易用，且拟合效果较好，这一点已在很多发达国家得到验证，如美国在养老金精算报告中对长寿风险进行度量时，采用的即是Lee-Carter模型。但也有部分研究显示Lee-Carter模型拟合中国人口死亡率时效果并不好，其主要原因是研究者未对中国人口死亡率进行调整与修匀，直接使用具有较大波动性的粗死亡率，会降低Lee-Carter模型拟合效果。因此，本文基于调整和修匀后的男性人口死亡率数据建立的Lee-Carter模型，具有更好的拟合优度。

3.4.2 男性人口预期寿命预测结果比较

(1)短期内的预测效果比较。本文选取2013～2019年男性人口预期寿命的实际值作为对照组，用以检验Lee-Carter模型和贝叶斯分层模型的短期预测效果。本文选取三个口径的男性人口预期寿命数据，以期获得更加稳健的检验结果。其中，2013～2014年、2016～2018年为1‰的变动抽样调查，中国国家统计局未直接公布男性人口预期寿命，采用调整和修匀后的男性死亡率计算预期寿命；2015年是1%的抽样调查，选取了中国国家统计局公布的男性人口预期寿命；对于2019年，选取了世界卫生组织发布的中国男性人口预期寿命的调查数据。本文将2013～2019年的调查数据计算值(实际值)、Lee-Carter模型预测值和贝叶斯分层模型预测值列示于表6中。由表6可见，对于2013～2019年的男性人口预期寿命，Lee-Carter模型预测值与实际值的差值绝对值分别为0.48、0.18、0.01、0.67、0.67、0.04和0.04；贝叶斯分层模型预测值与实际值的差值绝对值分别为1.48、1.06、0.75、0.02、0.13、0.40和0.38。在各个年份，Lee-Carter模型预测值与实际值的差值绝对值均显著小于贝叶斯分层模型。从另一个角度看，2013～2018年男性人口平均预期寿命的实际值增长了1.83岁、平均每年增长0.37岁；2013～2018年Lee-Carter模型预测的男性人口平均预期寿命的实际值增长了1.31岁、平均每年增长0.26岁；2013～2018年贝叶斯分层模型预测的男性人口平均预期寿命的实际值增长了0.75岁、平均每年增长0.15岁。由此可见，Lee-Carter模型预测的男性人口预期寿命的年增长量更接近实际值，即Lee-Carter模型的短期预测效果优于贝叶斯分层模型。

进一步，结合表2和表3中区间预测结果，本文将2015年作为一个特殊对照组，比较两个模型短期内的预测效果。其中，中国国家统计局公布的2015年男性人口预期寿命为73.64岁；Lee-Carter模型居中假设预测得到的男性预期寿命为73.63岁、高假设预测得到的男性预期寿命为73.70岁、低假设预测得到的男性预期寿命为73.56岁；贝叶斯分层模型居中假设预测得到的男性预期寿命为74.39岁、高假设预测得到的男性预期寿命为76.00岁，贝叶斯分层模型低假设预测得到的男性预期寿命为72.83岁。为了更显著的分析预测结果与实际结果的差异情况，取两种模型的预测结果与实际结果差值的绝对值。可见，基于Lee-Carter模型的2015年中国男性人口预期寿命预测值与实际值的接近程度最高，居中假设下与实际值仅差0.01岁、高假设下差值为0.06岁、低假设下差值为0.08岁，尽管Lee-Carter模型预测区间的开口较窄，但已将实际值覆盖进该区间；贝叶斯分层模型居中假设下预测值与实际值之间的差为0.75岁、高假设下差值为2.36岁、低假设下差值为0.81岁，该模型预测区间开口较大，也能够将实际值覆盖进去。综上可见，Lee-Carter模型在短期内的预测效果优于贝叶斯分层模型，与真实男性人口预期寿命更为接近。

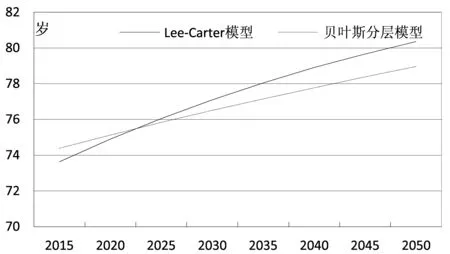
图1 2015～2050年中国男性人口预期寿命预测结果比较图

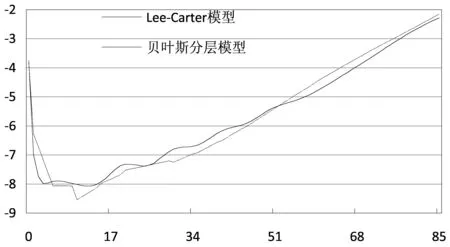
图2 2015年中国男性人口分年龄对数死亡率预测结果比较图

(2)长期中的变动趋势比较。通过图1展示2015～2050年两种模型方法下男性人口预期寿命预测结果的变动趋势图。可见，2015年Lee-Carter模型预测得到的男性人口预期寿命低于贝叶斯分层模型，然而随着时间的推移，二者之间的差异不断减小，直到2022年二者接近相等，随后Lee-Carter模型预测的男性人口预期寿命均高于贝叶斯分层模型，该趋势一直持续到2050年，且二者差距逐年增大。出现这种情况的原因在于，Lee-Carter模型假设了对数死亡率下降速度为常数，即对数死亡率呈线性下降趋势，从长期视角来看这种线性下降趋势将会突破人口极限年龄，违背了人类的生物规律。而贝叶斯分层模型很好地解决了这一问题，通过将人口极限年龄考虑到模型假设中，运用更符合寿命变化特征的逻辑斯蒂假设来构建模型，尽管短期内的拟合效果不如Lee-Carter模型，但长期预测能够得到更加合理的结果。

3.4.3 男性人口死亡率预测结果比较

图2展示了Lee-Carter模型和贝叶斯分层模型预测得到的2015年男性人口分年龄死亡概率(qx)的预测结果。

由图2可见，分层贝叶斯模型首先估计出男性人口预期寿命，然后采用模型生命表法计算出分年龄死亡率，在计算过程中对死亡率进行了修匀，因此死亡率曲线较为光滑；Lee-Carter模型方法针对修匀后的男性人口死亡率数据进行预测，对预测结果不再进行二次修匀，因此死亡率波动性略大。比较两种预测方法得到的男性人口死亡率年龄分布规律发现，50岁以下年龄组，Lee-Carter模型预测结果整体上高于贝叶斯分层模型预测结果；50岁以上年龄组，Lee-Carter模型预测结果逐渐低于贝叶斯分层模型预测结果。综合全年龄段来看，Lee-Carter模型预测的男性人口死亡率整体高于贝叶斯分层模型预测结果，也使得Lee-Carter模型计算得到的人口预期寿命值低于贝叶斯分层模型预测结果。

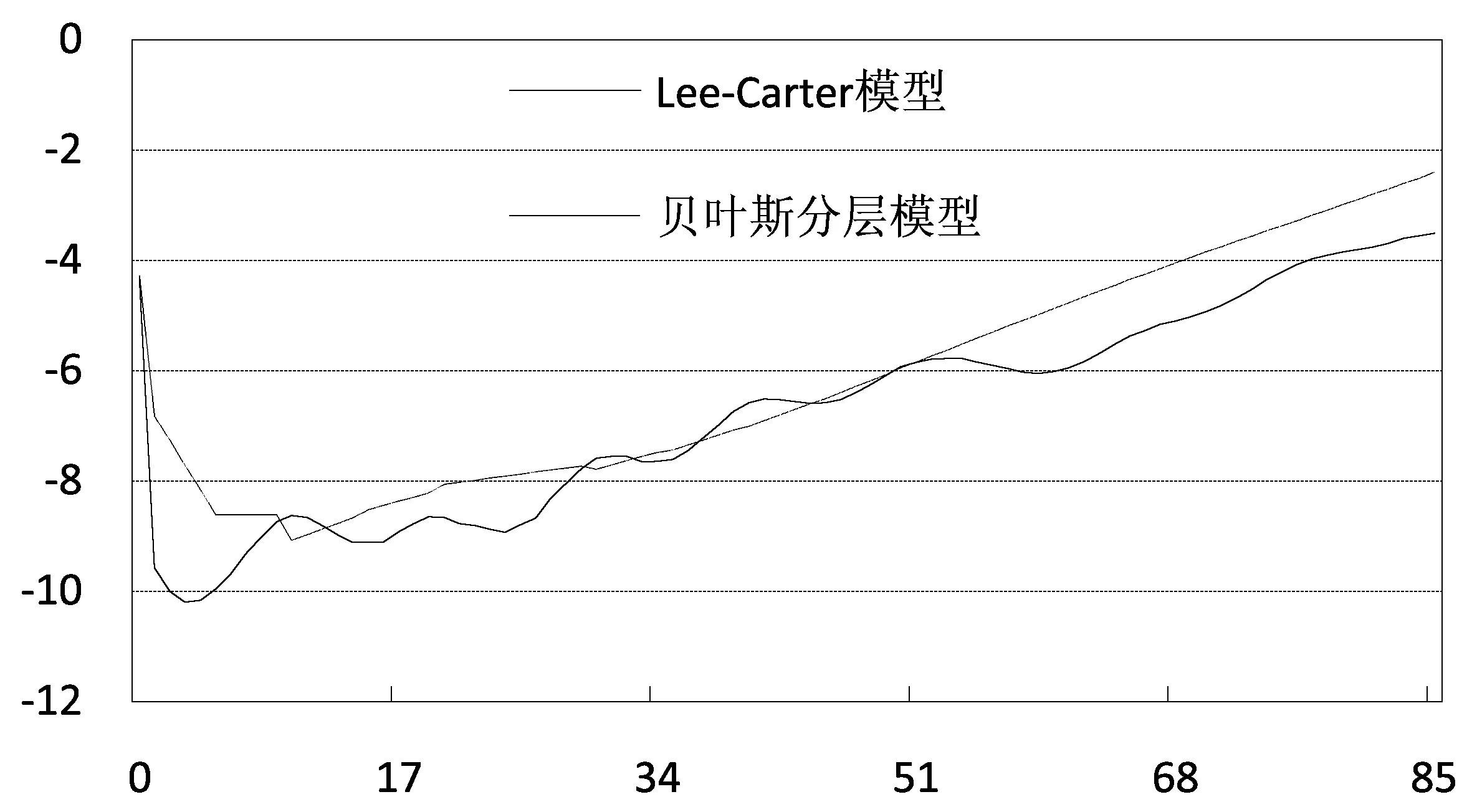
图3 2050年中国男性人口分年龄对数死亡率预测结果比较图

图3展示了Lee-Carter模型和贝叶斯分层模型预测得到的2050年中国男性人口分年龄死亡概率(qx)的预测结果。

在图3中，比较两种预测方法得到的男性人口死亡率年龄分布规律发现，30岁以下年龄组，Lee-Carter模型预测结果整体上低于贝叶斯分层模型预测结果；30～50岁，Lee-Carter模型预测结果与贝叶斯分层模型预测结果较为接近；50岁以上年龄组，Lee-Carter模型预测结果显著低于贝叶斯分层模型预测结果。综合全年龄段来看，Lee-Carter模型预测结果整体低于贝叶斯分层模型预测结果，也使得Lee-Carter模型计算得到的人口预期寿命值高于贝叶斯分层模型预测结果。

综合2015～2050年两种方法下的预测结果，Lee-Carter模型预测得到的男性人口死亡率结果，围绕着贝叶斯分层模型的预测结果自上而下的进行移动。即，2015年Lee-Carter模型得到的全年龄段男性人口死亡率高于贝叶斯分层模型结果，随着时间的推移，二者之间差距逐渐减小，并在2022年附近二者接近相等。随后，Lee-Carter模型得到的全年龄段男性人口死亡率开始小于贝叶斯分层模型结果，且一直持续至2050年。此外，随着年龄的增加，两种模型预测的男性人口死亡率变化趋势存在差异。其中，贝叶斯分层模型预测结果波动较小，随着年龄增长呈现出线性变化趋势；Lee-Carter模型得到的男性人口死亡率在年龄模式上拥有更丰富的信息，在全部年龄上呈分段的线性变化趋势，中低年龄组死亡率随年龄增长变动趋势的斜率较高，但中高年龄组变动趋势的斜率相对平缓，年龄分界点约为50岁。由于人口死亡率年龄模式上的差异会影响未来人口年龄结构，因此Lee-Carter模型预测结果能够获取更丰富的年龄模式特征，可以更好地解释未来人口年龄结构变化的原因。

4 研究结论

本文选用Lee-Carter模型和贝叶斯分层模型对中国男性人口死亡率进行动态预测，并将结果进行比较，得到如下结论：

第一，从模型对历史数据的拟合效果看，Lee-Carter模型在所选取的四种误差函数下计算得到的误差值均小于贝叶斯分层模型计算结果，拟合优度较高。由于本文拟合Lee-Carter模型时所采用的数据为修匀后死亡率数据，并参考国内学者的研究对新生婴儿死亡率进行了调整，使数据更加光滑，有助于提升Lee-Carter模型拟合效果。然而，贝叶斯分层模型前提假设、预设参数和主观因素较多，拟合的数据仅为人口预期寿命，数据中所包含的信息较少，尽管数据中能够体现其他国家人口预期寿命变动的先验信息，但在对中国历史死亡率数据拟合上效果并不如Lee-Carter模型。因此，采用Lee-Carter模型预测中国男性人口死亡率是一种相对较好的选择，但需避免直接采用波动较大的粗死亡率进行分析。

第二，从对人口预期寿命的预测情况来看，在短期内Lee-Carter模型和贝叶斯分层模型的预测区间均能将男性人口预期寿命实际值包含到其中，但居中假设下的预测精度有所不同。Lee-Carter模型预测结果与实际值相差较小，而贝叶斯分层模型预测结果与实际值的差异相对较大，即Lee-Carter模型具有较好的短期预测效果。然而，长期预测中Lee-Carter模型方法给出的预测区间开口较窄，而贝叶斯分层模型能够给出更宽的预测区间，提高了预测结果的稳健性。

第三，从对分年龄人口死亡率的预测来看，Lee-Carter模型的研究对象即为分年龄死亡率，因此预测结果能够体现出更丰富的年龄模式特征，如不同年龄人口死亡率改善程度的差异和波动情况的差异等。然而，贝叶斯分层模型的研究对象为人口预期寿命，分年龄死亡率是通过既定的模型生命表转换而来的，该方法会导致分年龄死亡率变动模式被模型生命表假设所掩盖，影响对未来人口年龄结构的判断。

第四，从预测的人口死亡率下降速度或人口预期寿命提高速度来看，Lee-Carter模型假设人口死亡率改善因子为常数，即假设未来人口死亡率的下降速度仍保持历史水平不变，而贝叶斯分层模型中的人口预期寿命服从逻辑斯蒂假设，即寿命增长呈现先快后慢的S型曲线变动趋势。因此，Lee-Carter模型预测得到的短期男性人口死亡率高于贝叶斯分层模型，预期寿命低于贝叶斯分层模型；随着时间的推移，Lee-Carter模型预测的男性人口死亡率能保持之前相同的幅度下降，而贝叶斯分层模型则减慢了死亡率下降速度，2025年之后Lee-Carter模型预测的分年龄死亡率整体低于贝叶斯分层模型，而预期寿命高于贝叶斯分层模型。从发达国家经验来看，随着经济的增长，人口死亡率的改善速度会呈现先快后慢的趋势，伴随而来的人口预期寿命的增长也会呈现先快后慢的趋势，贝叶斯分层模型能够更好地刻画这一特征。