基于自适应控制的四元数时滞神经网络的有限时间同步*

赵 玮，任凤丽

（南京航空航天大学 数学系，南京 211106）

引 言

近几十年来，神经网络受到了长久的关注.这与神经网络在保密通信、模式识别、联想记忆等多个领域的广泛应用有直接关系[1].神经网络复杂的动力学行为如稳定、同步、分岔也推动了神经网络的广泛研究[2-4].

四元数是一个非常有趣的话题.四元数问题首先于1843年被英国数学家Hamilton W R 所研究，对比于常见的实值、复值问题，四元数在运算规则上不具有乘法交换律.因此，四元数的研究一度处于停滞的状态.作为实值、复值的延展，四元数问题具有更加广泛的应用，尤其在最近几年人们相继地将四元数引入到神经网络中[5-10].四元数神经网络同常见的实值、复值神经网络相比，能有效地减少系统的维数，具有可靠的计算速率[7].因此，四元数系统在优化方面具有更好的应用.文献[8]研究了四元数神经网络的全局稳定性问题.借助于线性矩阵不等式方法，文献[9]得到了四元数神经网络全局µ 稳定的判据.文献[10]研究了四元数神经网络多平衡点的稳定性问题.上述文献绝大多数只考虑了稳定性问题，对四元数神经网络同步现象的研究相对较少，通过实虚部分离的方法，本文研究了四元数神经网络的同步问题.

实际应用中，常常要求系统具备有限时间稳定的性能，因此，系统的有限时间稳定受到了大量学者的广泛关注.有限时间稳定系统相比于渐近稳定等具有较快的收敛速率、有限时间的稳定、抗干扰等优势.文献[11]分别设计了两种不连续的控制协议使得系统在有限时间内实现一致.文献[12]通过使用隐函数方法给出了系统有限时间稳定的基本判据并给出了停息时间的估计.文献[13]通过用反函数方法解释了有限时间稳定的本质原因并有效地应用到了复杂网络的有限时间同步.由于实际系统中存在着多个平衡点问题，因此，文献[14]给出了系统有限时间半稳定的定义，并因此受到了学者的广泛关注.最近的有限时间稳定研究成果见文献[15-18].

基于上述成果的启发，本文主要研究了四元数时滞神经网络的主从系统有限时间同步.本文的主要贡献在于：1) 首次考虑了四元数时滞神经网络的有限时间自适应同步问题，设计了一组新颖的控制器和自适应定律.分析了自适应控制器下四元数时滞神经网络的有限时间同步，并给出了停息时间的估计.借助Lyapunov 函数和不等式方法，得到了四元数时滞神经网络主从系统同步的充分条件.2) 由于神经元的传输过程中不可避免地出现时滞，本文考虑了四元数神经网络在时滞情形下的有限时间同步.文章主要由以下几个部分组成：在第1 节，给出了基本定义、模型；第2 节给出了主要定理和证明；在第3 节，通过数值模拟验证了定理的有效性；最后，第4 节给出了总结和展望.

符号说明：N 表示非负整数集合，Rn表示n维实空间；Q表示四元数的集合；|·|Q表示四元数的模；D+f(t)表示f(t)的右上Dini 导数.

1 基本定义和模型

一个四元数可由一个实部和三个虚部组成，如w=wR+wIi+wJj+wKk，这里w∈Q，wR,wI,wJ,wK∈R，虚部i,j,k 满足Hamilton 准则：

i2=j2=k2=−1,ij=−ji=k,jk=−kj=i,ki=−ik=j.

注1四元数是一种超越数，由实值和复值演变而来，然而运算法则不满足乘法交换律，即x,y∈Q,xy≠yx.

记w的共轭：=wR−wIi−wJj−wKk，w的模：|w|Q=

加法定律：对于任意两个四元数h,q∈Q，h=hR+hIi+hJj+hKk，q=qR+qIi+qJj+qKk，h+q=hR+qR+(hI+qI)i+(hJ+qJ)j+(hK+qK)k；

乘法定律：基于Hamilton 准则，可得

hq=(hRqR−hIqI−hJqJ−hKqK)+(hRqI+hIqR+hJqK−hKqJ)i+

(hRqJ+hJqR+hKqI−hIqK)j+(hRqK+hKqR+hIqJ−hJqI)k.

四元数时滞神经网络的一般形式可描述如下：

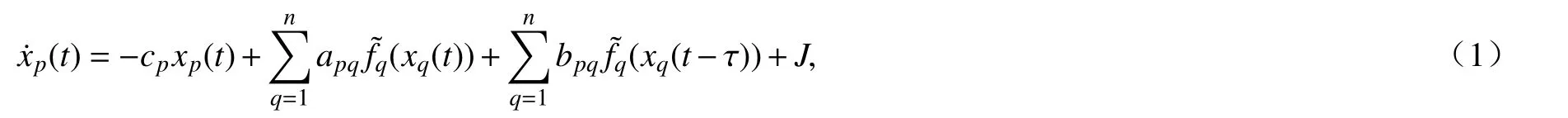
这里p=1,2,···,n，xp(t)∈Q表示第p个神经元的状态，cp>0 表示第p个神经元的自反馈系数，apq表示神经元p,q在时刻t的连接权重，bpq表示神经元p,q在时刻t−τ的连接权重，其中τ >0 表示离散时滞，(·)表示神经元q的激活函数，J表示系统的外部输入.系统(1)的初始条件为xp(t)=φ(t),t∈[−τ,0].

假设1对于任意的xp=xRp+xIpi+xJpj+xKpk，其中xRp,xIp,xJp,xKp∈R，p=1,2,···,n.激活函数满足

假设2对于任意的xαp,yαp∈R，存在常数lαp>0，p=1,2,···,n，α=R,I,J,K，满足

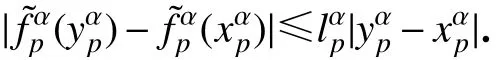
本文将系统(1)设为主系统，从系统用下式表示：

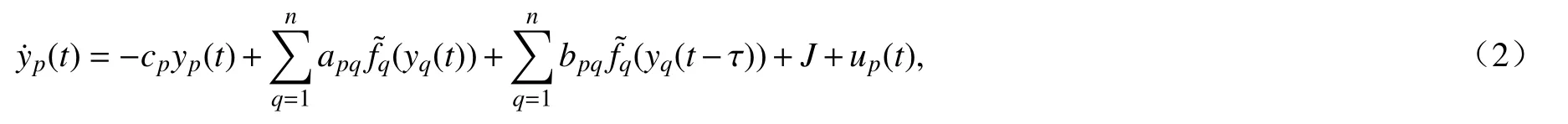
其中cp∈R，apq,bpq∈Q同系统(1)，up(t)是一个旨在实现主从系统有限时间同步的外部控制器.从系统(2)的初始条件为yp(t)=φ(t),t∈[−τ,0].

定义主系统(1)和从系统(2)之间的误差：ep(t)=yp(t)−xp(t)，则误差系统可用下述方程表述：

基于Hamilton 准则，将误差系统(3)进行实虚部分离得

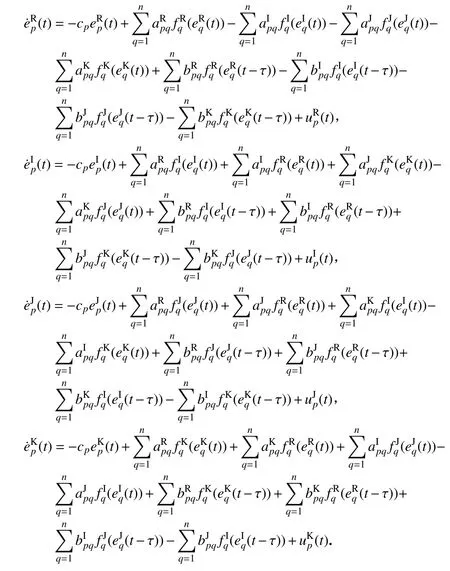
控制器设计如下：

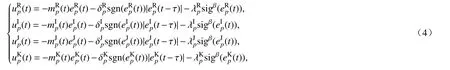
这里

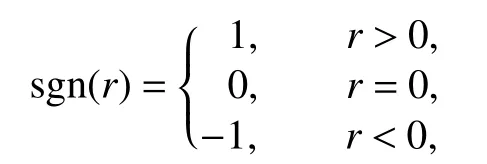
sigβ(r)=sgn(r)|r|β，0<β<1，δαp>0，λαp>0，α=R,I,J,K.

注2全文将在Filippov 解意义下[19]讨论系统(3)能否有限时间收敛到零.

下面将主要介绍有限时间同步的定义和基本引理.

定义1若存在T>0，使得

1) l imt→T|yp(t)−xp(t)|=0；

2) |yp(t)−xp(t)|=0,t≥T

成立，则主系统(1)和从系统(2)实现有限时间同步，其中T称为停息时间.

引理1[20]假定V(t)是连续正定的函数且满足下式：

D+V(t)≤µVϑ(t),

这里µ >0，0 <ϑ<1，对任意的t≥t0均成立，则有以下的不等式成立：

V1−ϑ(t)≤V1−ϑ(t0)−µ(1−ϑ)(t−t0),t0≤t≤T,

其中V(t)=0，t≥T，T=t0+V1−ϑ(t0)/(µ(1−ϑ)).

引理2[21]设x1,x2,···,xn≥0，0 1，则有

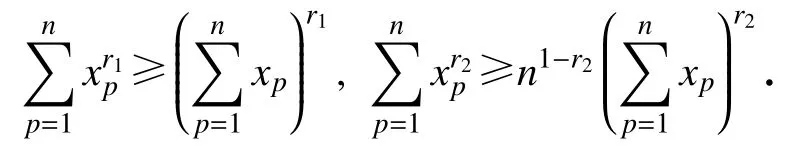
2 主要结果

本节将通过上文给定的自适应控制器，基于Lyapunov 稳定性理论给出两个四元数神经网络即主系统(1)和从系统(2)的有限时间同步的充分条件.

定理1在假设1 和假设2 下，误差系统 (3)在控制器(4)伴随的更新定律为式(5)，主系统(1)和从系统(2)实现有限时间同步，停息时间

证明构造候选Lyapunov 函数V(t)=V1(t)+V2(t)+V3(t)+V4(t),

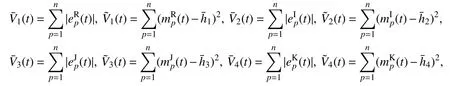
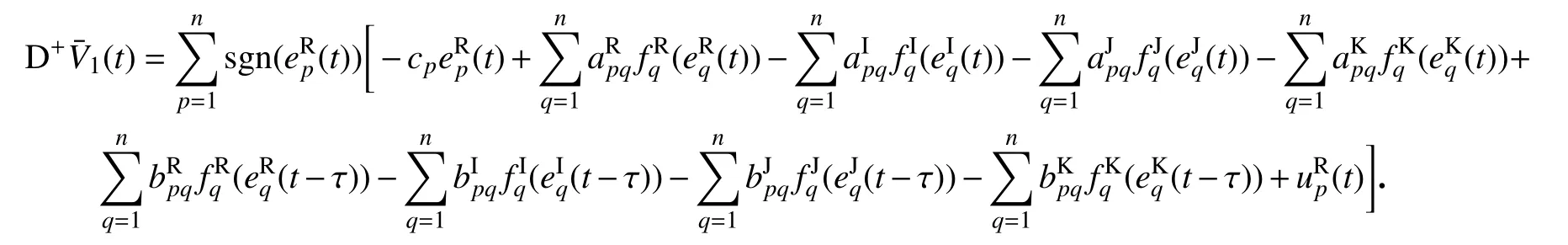
对辅助函数(t)求右上Dini 导数，得

由假设2 得

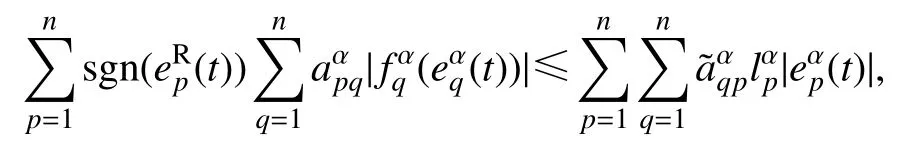
这里α=R,I,J,K.则有下式：

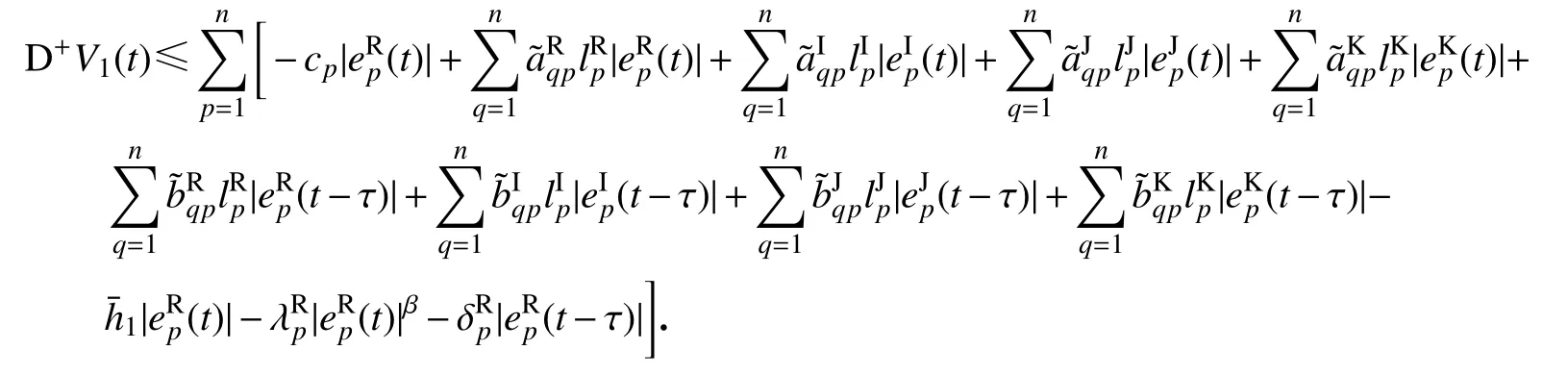
同理可得

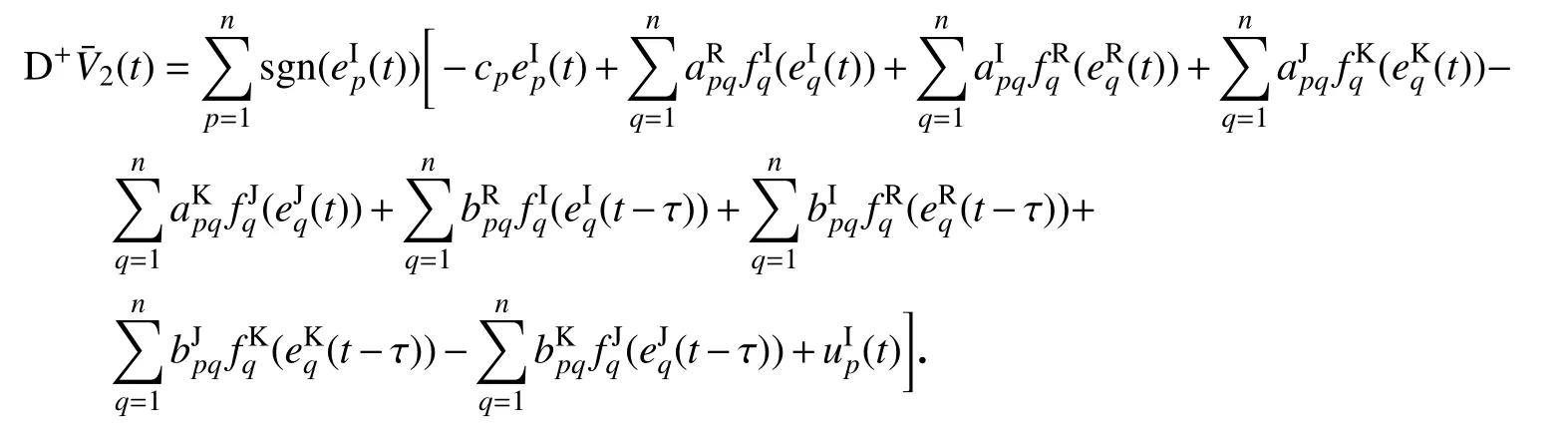
对辅助函数(t)求右上Dini 导数，得

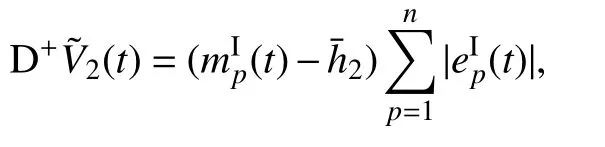
则有下式：

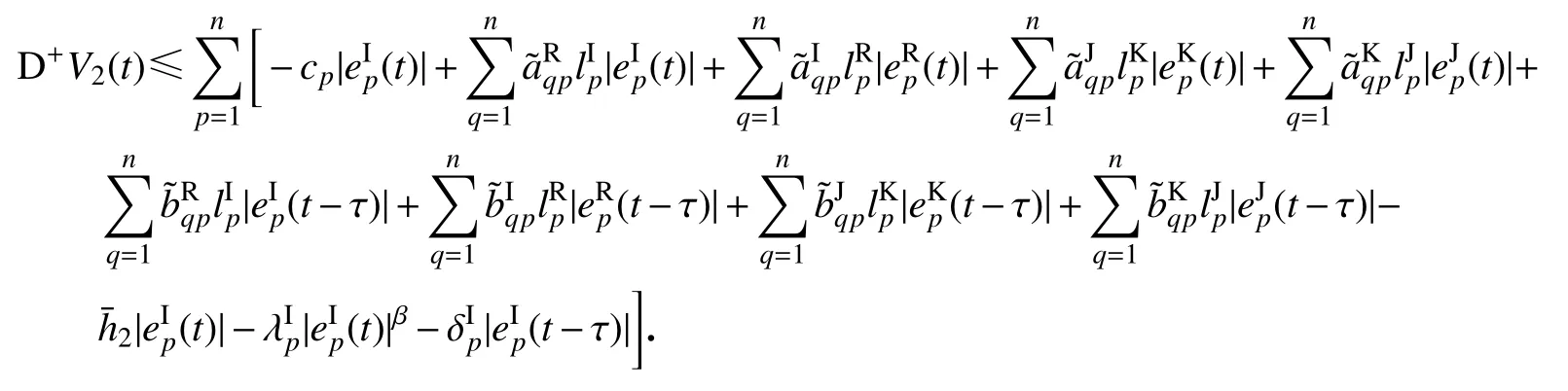
同理可得

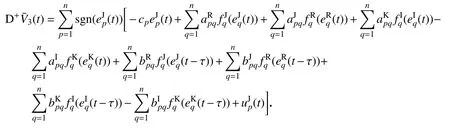
对辅助函数(t)求右上Dini 导数，得

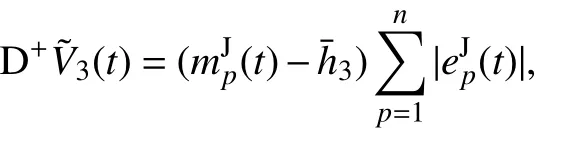
则有下式：

同理可得

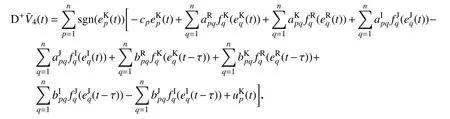
对辅助函数(t)求右上Dini 导数，得

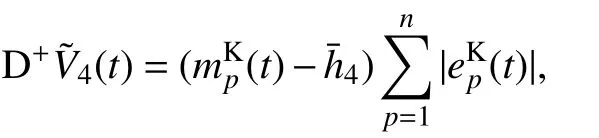
则有下式：

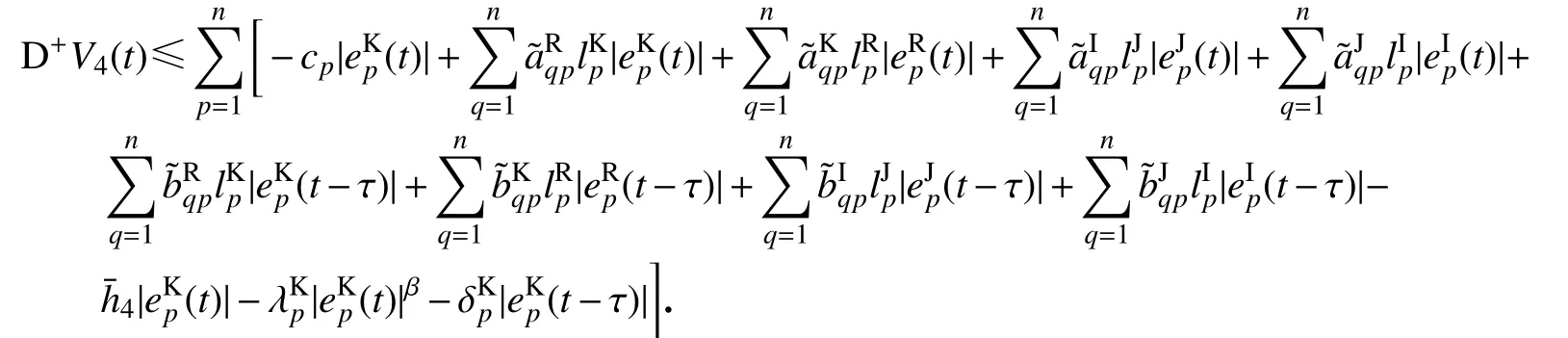
综合上式，得

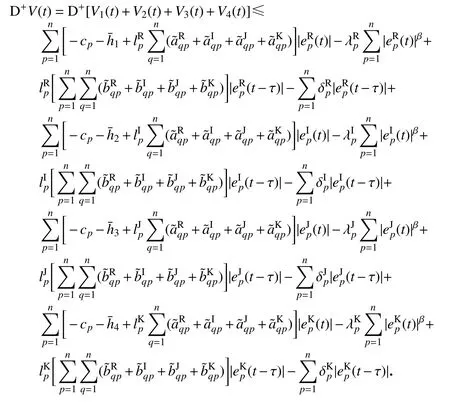
根据引理2，则下列不等式成立：

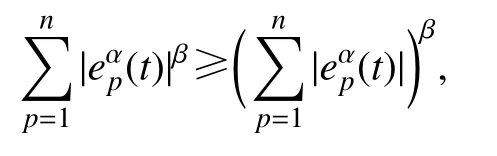
其中 0 <β<1.

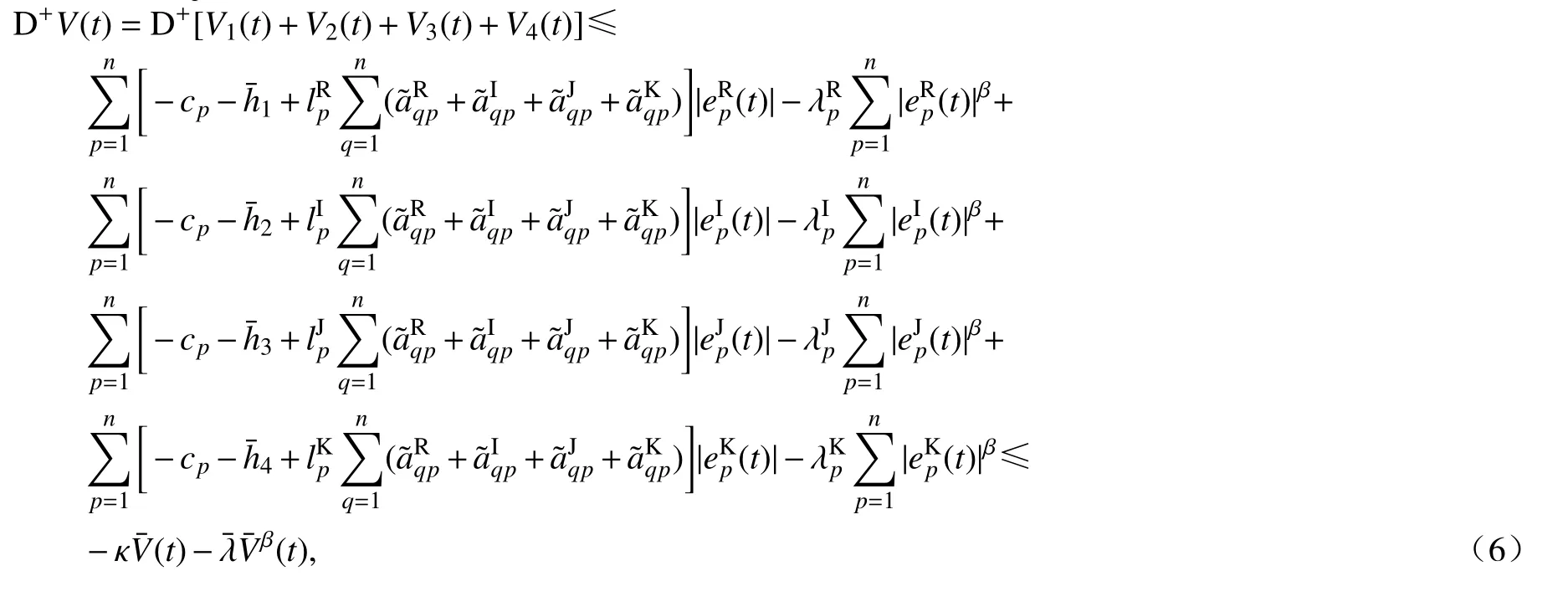
其中

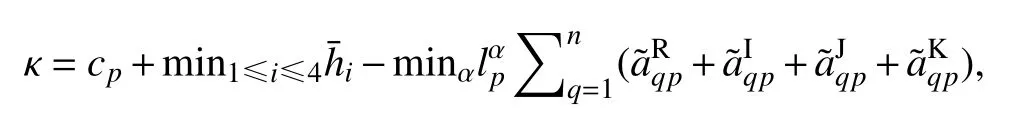
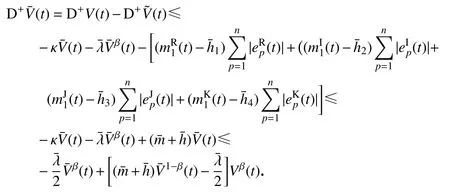
定义一个常数

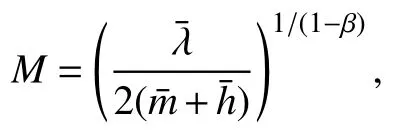
取

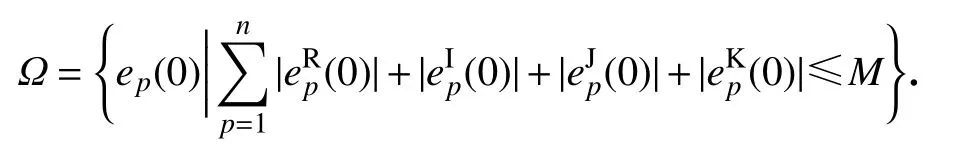
下面将考虑两种情形.

情形1若(0)≤M，于是可得根据引理1，则系统(3)有限时间收敛到零.系统的停息时间估计

情形2若(0)>M，采用反证法，若对任意的时刻t，(t)>M恒成立，则有下式成立：

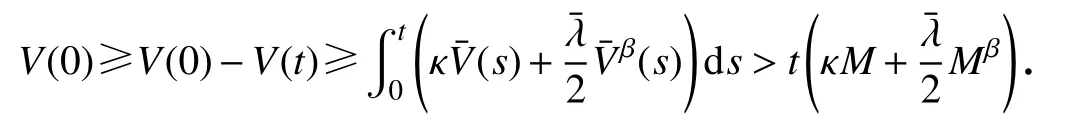
3 数值模拟

考虑四元数细胞时滞神经网络的主系统(1)与从系统(2)，系统参数的取值如下：c1=1.5,c2=1,a11=b11=1+2i+2j+2k,a12=b12=2+i+2j+1.5k,a21=b21=1+2i+j+0.5k,a22=b22=2+2i+2j+k.取n=2,=取mα1(t),mα2(t),α=R,I,J,K的初值为mR1(0)=0.1,mI1(0)=0.2,mJ1(0)=0.4,mK1(0)=0.2,mR2(0)=0.2,mI2(0)=0.3,mJ2(0)=0.4,mK2(0)=0.6,β=0.8,λαp=6.由此可知lαp=1,α=R,I,J,K.通过定理1的条件取 δα1=12，δα2=15.随机取4 组 [−1,1]间的初值，步长h=1×10−3.从图1、图2可知主系统(1)与从系统(2)是有限时间同步的.

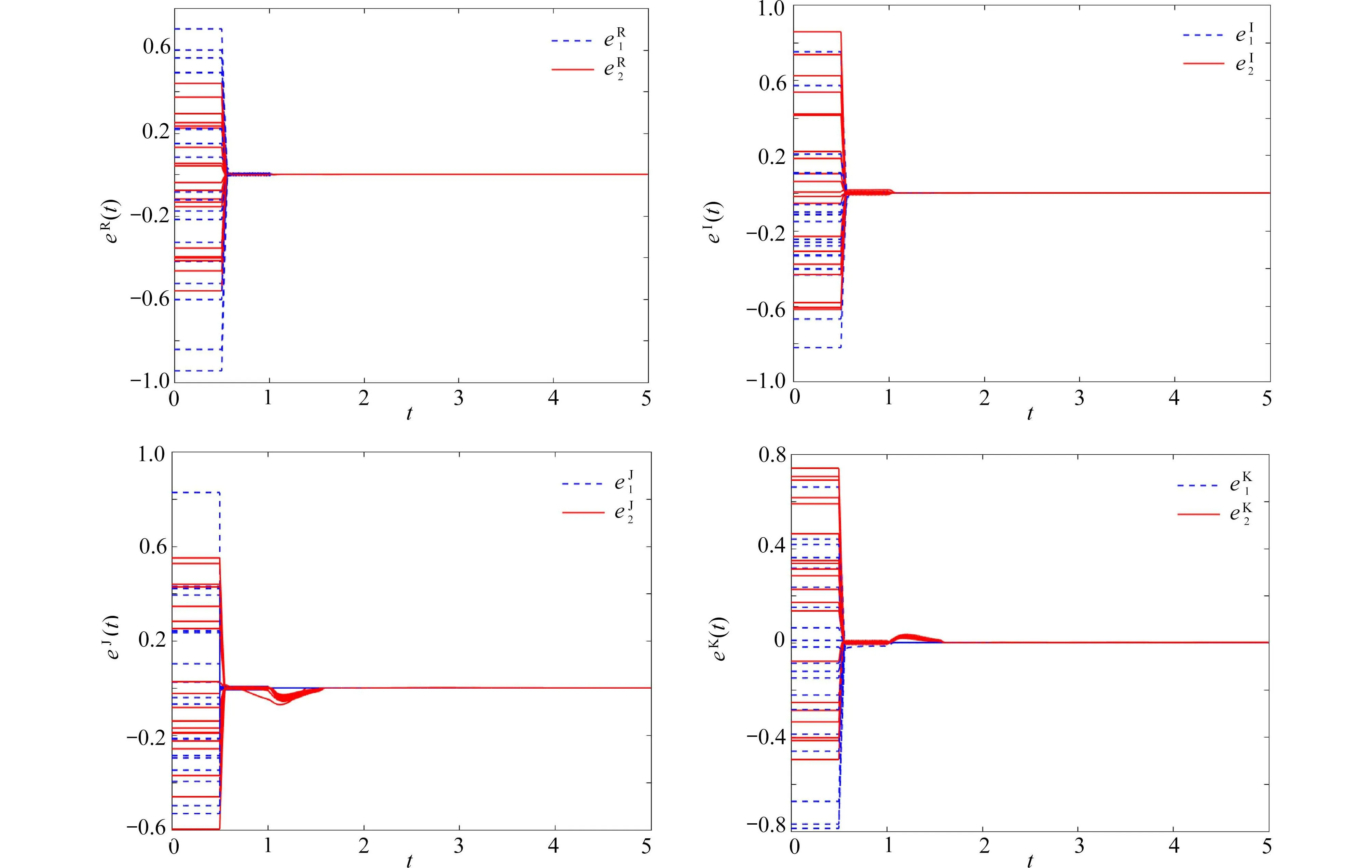
图1 误差状态的实、虚部运动轨迹Fig.1 The trajectories of the real，imaginary parts of errors

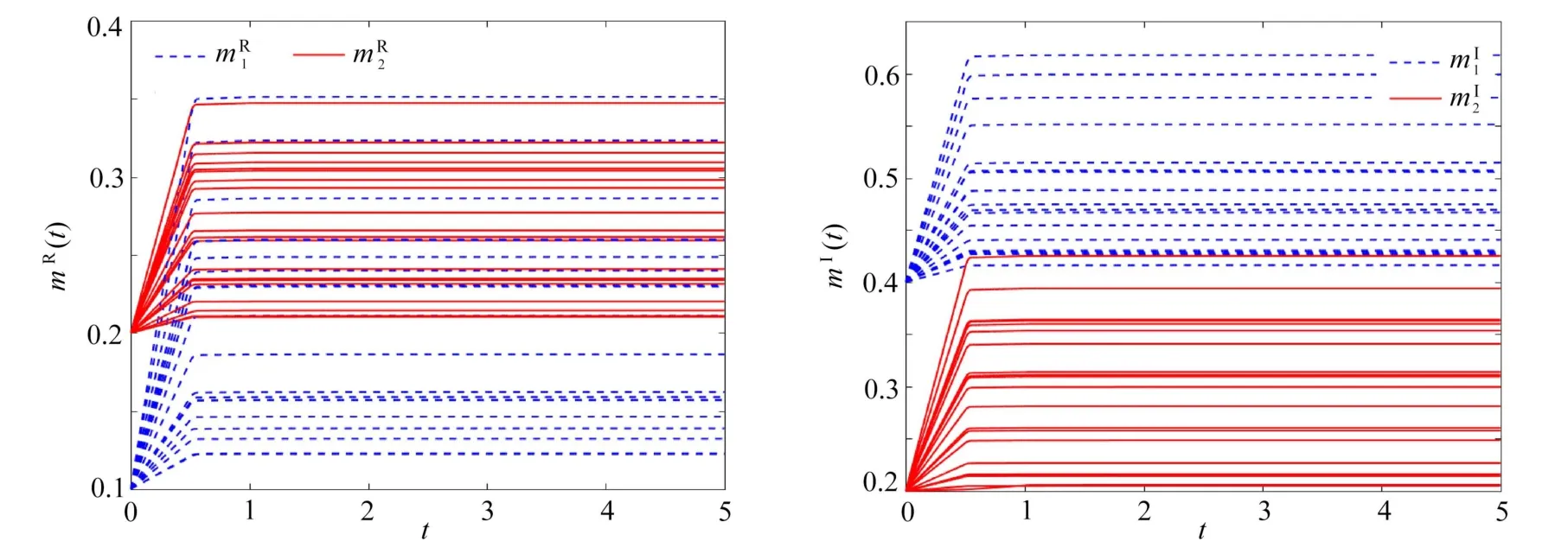
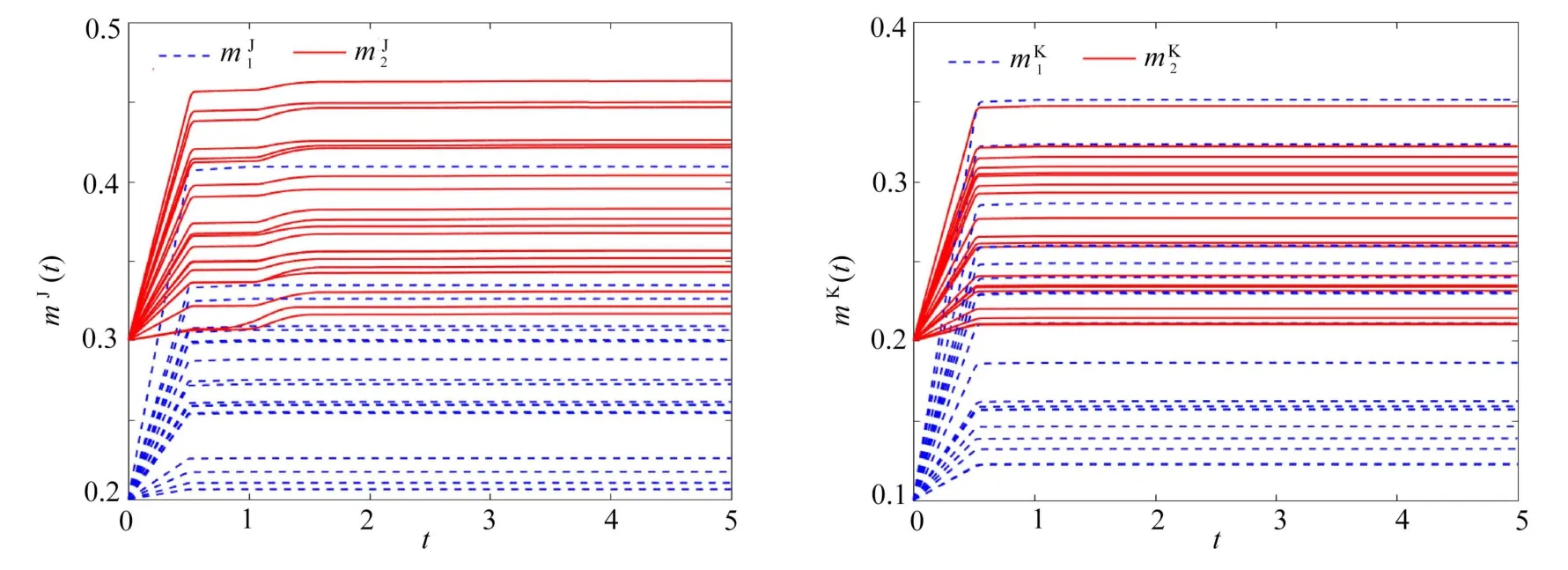
图2 自适应增益的实、虚部运动轨迹Fig.2 The trajectories of the real，imaginary parts of adaptive gain

4 结 论

本文研究了四元数时滞神经网络的有限时间同步问题.为节约控制成本，设计了一组新颖的自适应控制器，基于Lyapunov 稳定性理论和不等式方法，有效地解决了含有时滞的四元数神经网络主从系统的有限时间同步.对比已有文献关于四元数神经网络的研究，首次研究了自适应控制下四元数时滞神经网络的有限时间同步.四元数作为实值、复值的延伸，具有较为广泛的应用价值.因此本文所考虑的四元数时滞神经网络的有限时间同步更具有一般性.通过数值仿真有效地验证了定理的合理性.考虑到离散时间的四元数神经网络的有限时间自适应稳定和四元数神经网络的切换同步对实际应用有非常重要的意义，因此，笔者未来将主要关注四元数切换系统下的有限时间同步和四元数离散神经网络的有限时间自适应同步控制问题.