Vallis系统的不变代数曲面研究*
杨 静,谈文慧,魏周超
(中国地质大学(武汉) 数学与物理学院,武汉 430074)
引 言
一些经典的三维混沌系统虽然形式很简单,但其动力学性质却极为复杂[1-2].为了便于研究,学者们往往会通过证明系统的可积性,以及寻找系统的不变代数曲面,从而将系统降维,以此达到简化系统的目的.此外,若一个微分系统有足够多的首次积分,则可证明此微分系统是可积的,从而就可以找到系统的不变代数曲面.通过将系统限制在不变代数曲面上,然后研究不变代数曲面上的动力学性质,这对我们研究系统的整体动力学性质起着非常重要的辅助作用.因此,研究微分系统的可积性和不变代数曲面是非常有必要的.在学者们的研究过程中,如何去寻找系统的首次积分就成了问题的关键,但遗憾的是,目前并没有一个通用有效的方法可以解决此问题.Darboux 多项式与首次积分的联系密切,可以通过研究系统的Darboux 多项式来寻找系统的首次积分,或者通过证明系统不存在Darboux 多项式,进而推出系统不存在首次积分.但同样地,寻找系统的Darboux 多项式也是一个困难的问题,目前仍有许多难题需要被解决.
学者们对动力系统的代数可积性及不变代数曲面问题的研究,可以追溯到Darboux[3]和Poincar[4]的研究:Darboux 最早给出了代数几何与寻找首次积分之间的联系;Poincar则研究了有理首次积分,并提出:寻找一个多项式向量场的Darboux 多项式是一项非常困难的任务,目前还没有找到一个有效的方法去计算它.1996年,Labrunie 通过初等微分代数方法[5],计算出了Lotka-Volterra 系统的所有多项式一阶积分[6].1999年,Ollagnier 基于代数和组合学的思想,研究了Lotka-Volterra 系统的齐次有理首次积分[7].2000年,Llibre 等利用求解线性偏微分方程的特征曲线方法,描述了Rikitake 系统的所有不变代数曲面.此外,Llibre 等还证明出在某些参数条件下,系统存在一个多项式首次积分或有理首次积分[8].2002年,Llibre 等使用加权齐次多项式和特征曲线的方法,通过求解线性偏微分方程,对经典Lorenz 系统的所有Darboux 不变量、不可约Darboux 多项式、有理首次积分及代数可积性进行了分类讨论[9].2002年,Swinnerton-Dyer 通过对多项式权值的重新定义,分析并计算了Lorenz 系统的不变代数曲面[10].2007年,Lü等通过使用加权齐次多项式和特征曲线法,研究了Chen 系统的Darboux 多项式和代数可积性问题[11].2011年,Deng 等通过对多项式权值的重新定义,求出了Chen 系统的所有不变代数曲面[12].2018年,Murilo 等研究了一个金融模型的不变代数曲面和Hopf 分岔问题,并基于加权齐次多项式和特征曲线的方法,证明出该模型对于任何参数值都不存在不变代数曲面[13].2018年,Aybar 等利用计算机代数工具,研究了一个二次自相互作用的二饵一捕食者系统的动力学性质,并给出了该系统存在不变代数曲面的条件[14].2019年,Ferragut 等研究了一类平面多项式向量场的Darboux 首次积分问题,证明了这些向量场具有扩展的约简过程,并给出计算系统Darboux 首次积分的算法[15].2020年,Dias 等利用Poincar紧化,对一个病毒系统做全局分析,证明出对于两组参数值,系统具有不变代数曲面[16].同年,Dias 等利用三维空间中的Poincar紧化,对Maxwell-Bloch 系统进行了全局分析,证明出对于某些参数值,该系统具有首次积分和不变代数曲面[17].
ENSO (El Niño southern oscillation)现象是指太平洋东部和中部大规模变暖的现象,这种现象的产生与热带太平洋海洋-大气系统的无序性和地球上最突出的气候变化有关,一般会持续几个月.ENSO 现象会对当地渔业及海洋生物的迁移产生巨大的影响,并且热带海洋表面温度场对全球气候也会产生不容忽视的影响,这些影响使学者们对ENSO 现象产生了极大的兴趣.在文献[18-21]中,学者们都针对ENSO 现象提出了模型,并成功地解决了部分问题,但这些模型都比较复杂.1988年,Vallis 在研究ENSO 现象时,提出了一个简化的微分方程组,即Vallis 模型[22].Vallis 系统是一个三维微分系统,它模拟了太平洋热带地区的大气动力学与年降水量、气温和风力的变化有关.本文引入Vallis 系统如下:

式中变量x表示风力,变量y表示太平洋东西部近水面温差,变量z表示近水面平均温度,参数b和c为正实数,P为实数.
尽管Vallis 模型忽略了地球自转、压力场和波动现象等一些影响,但它提供了对观测到的过程的正确描述,并描述出许多观测到的ENSO 现象.2008年,Krishchenko 等利用Vallis 模型,研究了右侧可微时变系统紧不变集的局部化问题[23].在文献[24]中,Euzebio 等讨论了Vallis 系统的周期解的存在性及稳定性问题.2015年,Garay 等研究了Vallis 模型的混沌问题[25].2017年,Borghezan 等分析了Vallis 系统的混沌与周期性,证明了嵌入在混沌区域的周期结构的存在性,并且这些周期结构是以周期相加序列的形式存在的[26].2019年,Rajagopal 等研究了Vallis 模型的反单调性、分岔性和多稳定性问题,分别给出了当P为0 和不为0 时产生Hopf 分岔的参数条件[27].在本文中,我们将从代数学方面,研究系统(1)的Darboux 多项式和不变代数曲面问题.
本论文构造如下:第1 节给出了一些Darboux 多项式的相关定义及求解线性偏微分方程的特征方法,并给出了本文的主要定理;第2 节给出了主要定理的证明;第3 节给出了本文的总结.
1 主要结论和定义
设f(x,y,z)是关于变量x,y,z的实多项式,若我们称f是系统(1)的Darboux 多项式,其中k(x,y,z)是实多项式,k称为f的余因子.由于系统(1)是三维二次系统,则由可知,余因子k(x,y,z)的阶数至多为1.若f(x,y,z)是Darboux 多项式且f=0是曲面,那么它就是不变的,我们称为不变代数曲面.
对X∈Rn,若存在S=(s1,s2,···,sn)∈Nn,m∈N,对所有α ∈R{0},有g(αsX)=g(αs1x1,αs2x2,···,αsnxn)=αmg(X),则多项式g(X)被 称为加权齐次的,其中R 代表实数域,N代 表正整数集.我们称s为g的权,m表示加权阶数,X→αsX表示赋予变量新的加权次数.
为了方便读者理解,我们将求解线性偏微分方程的特征方法总结如下.考虑一阶线性偏微分方程:
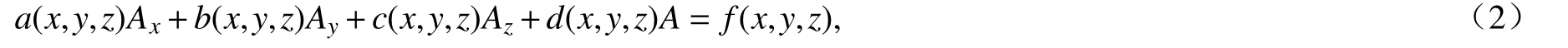
这里A=A(x,y,z),a,b,c,d,f是C1函数,Ax,Ay,Az分别是A(x,y,z)关于x,y,z的一阶偏导.
对于xyz空间中的曲线(x(t),y(t),z(t)),若对曲线上的每一点(x0,y0,z0),向量(a(x0,y0,z0),b(x0,y0,z0),c(x0,y0,z0))与曲线相切,则曲线(x(t),y(t),z(t))被称为线性偏微分方程(2)的特征曲线.并且,特征曲线是如下系统的解:
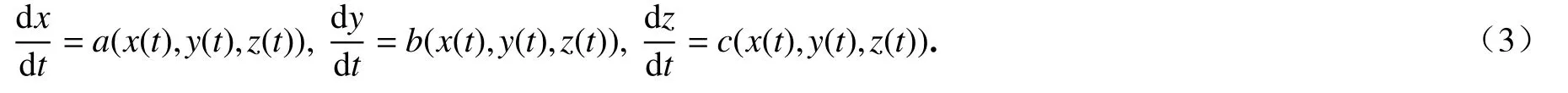
为了方便起见,我们将z代替t作为新的自变量,将系统(3)简化为如下方程(这里假设c(x(t),y(t),z(t))≠0):

则常微分方程(4)称为偏微分方程(2)的特征方程.
假设方程(4)有隐式解g(x,y,z)=c1,h(x,y,z)=c2,其中c1,c2是任意常数.现考虑如下变量替换:

且变换(5)的逆变换为x=p(u,v,w),y=q(u,v,w),z=s(u,v,w).于是我们将方程(2)变成关于w的常微分方程(对于固定的u,v):

本文的主要定理如下.
定理1当有以下条件之一成立时,系统(1)有不变代数曲面.
(ⅰ) 当c=1/2,P=0时,系统(1)的Darboux 多项式为an(x2+2bz−2b)2n,对应的余因子为k=−2n;另一个Darboux 多项式为an(x2+2bz−2b)2n−1,对应的余因子为−2n+1,其中an为任意非零实数.
(ⅱ) 当c=1,P=0时,系统(1)的Darboux 多项式为对应的余因子为k=−2n,其中a0为任意非零实数.
2 定理1的证明
通过变量替换

我们将系统(1)变为

接下来,我们继续对系统(8)做变量替换:

则系统(8)变为

其中上标点表示变量对T的导数.
若f(x,y,z)是系统(1)的一个Darboux 多项式,其余因子为k(x,y,z).不失一般性,我们假设k(x,y,z)=k0+k1x+k2y+k3z.令F(X,Y,Z)=αl f(α−1X,α−2Y,α−2Z),K(X,Y,Z)=α2k(α−1X,α−2Y,α−2Z),其中l为f的权齐次分量中的最高权次,(x,y,z)的权次为(1,2,2).假设F=F0+αF1+α2F2+···+αmFm,这里Fi是一个权齐次多项式,其权次为l−i,且i=0,1,···,m,l≥m.由Darboux 多项式定义,我们可以得到以下等式:
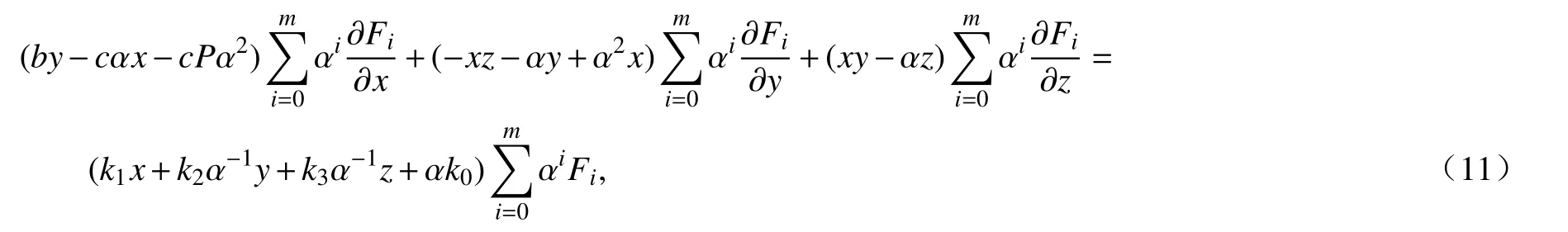
式中,我们仍用x,y,z代替X,Y,Z.比较等式(11)两边 α−1的系数,可以证明k2=k3=0.再比较等式(11)两边αi,i=0,1,···,m+2的系数,我们有
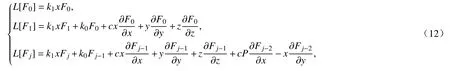
其中j=2,3,···,m+2;当j>m时,Fj=0;L是线性偏微分算子,

那么与线性偏微分算子(13)相关的特征方程为

经计算,特征方程(14)的通解为x2−2az=d1,y2+z2=d2,此处d1和d2是积分常数.接下来,我们做变量替换:

则变换(15)的逆变换是

在后面的计算中,为了方便,我们只考虑

通过变换(15)和(17),方程(12)的第一个方程变为如下常微分方程(对于固定的u,v):


这里G0是关于u,v的任意光滑函数.为了使是一个权齐次多项式,我们必须使k1=0,于是有
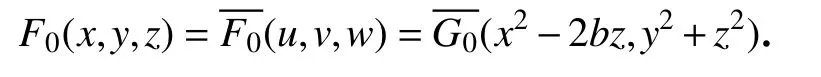
因此,系统(1)的每个Darboux 多项式的余因子是一个常数.由于u和v在x,y,z中的权次分别是2 和4,则F0的权次应为l=4n或l=4n−2,n∈N.所以F0的形式为

此处l=4n,且当i=0,1,···,n时,ai是任意实数;或

此处l=4n−2,且当i=1,2,···,n时,ai是任意实数.
对于这两种不同的情况,我们将证明分为两部分.
2.1 F0的形式为式(20)
将F0代入式(12)的第二个方程,我们可以证明
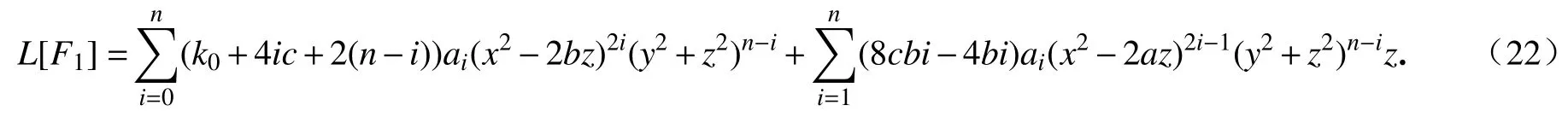
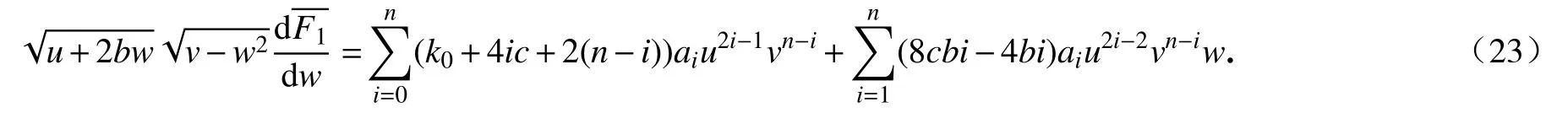
将方程(23)对w积分,我们得到

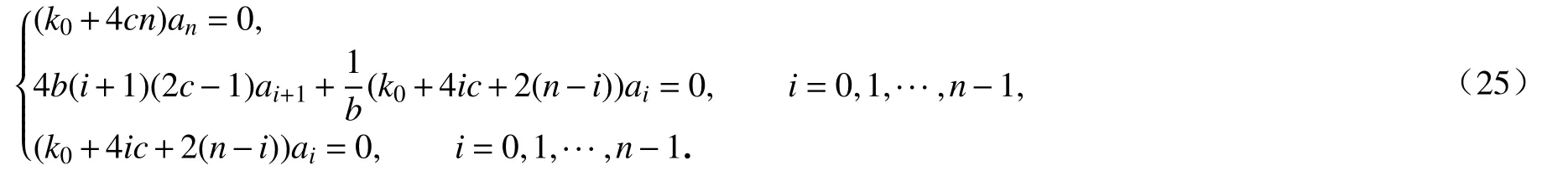
进一步,条件(25)可等同以下条件:
(ⅰ)c=1/2,k0=−2n,且存在i0∈0,1,···,n,使得ai0≠0;
(ⅱ)c≠1/2,k0=−2n,a0≠0,对i=1,2,···,n,有ai=0.
这里对两个条件进行说明,我们首先假设2c−1=0.于是条件(25)可以被简化为

由式(26)可以看出,当k0≠−2n时,对i=0,1,···,n,有ai=0,此时F0=0.将F0=0代入式(11),可以发现,对i=1,2,···,n,有Fi=0,则F=0,Darboux 多项式不存在;当k0=−2n时,对i=0,1,···,n,ai可以为任意实数,但须存在i0∈0,1,···,n,使得ai0≠0(否则有F0=0 ),即为条件(ⅰ);现在我们假设 2c−1≠0,由式(25)的第二个式子可以看出,若a0=0,则一定有a1=0,同理递推,对i=2,3,···,n,有ai=0,所以a0≠0(否则有F0=0);在式(25)的第二个式子和第三个式子中,令i=0,则有

由于a0≠0,则必须有k0+2n=0,于是可以得到a1=0,递推有ai=0,i=2,3,···,n,即为条件(ⅱ).
接下来,我们分别在这两个条件下进行计算.
条件(ⅰ) 当c=1/2,k0=−2n,且存在i0∈0,1,···,n,使得ai0≠0时,有F1=0.由式(11),当j=2时,计算得
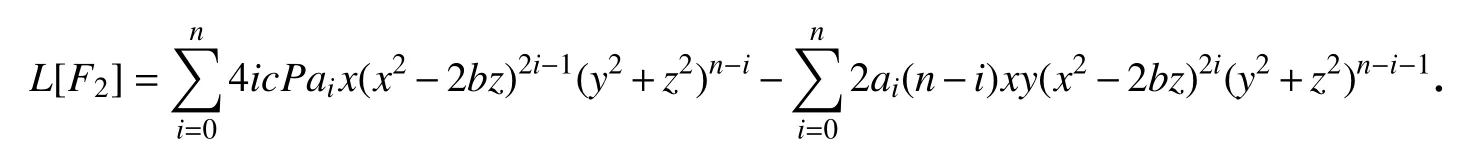
通过使用变换(15)和(17),我们得到以下常微分方程:
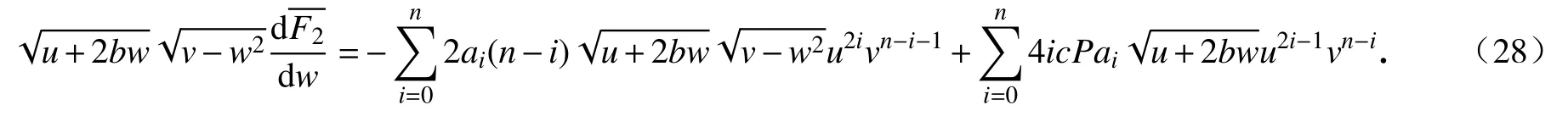
将方程(28)关于w求积分,得到


由条件(ⅰ),我们得到P=0,且有
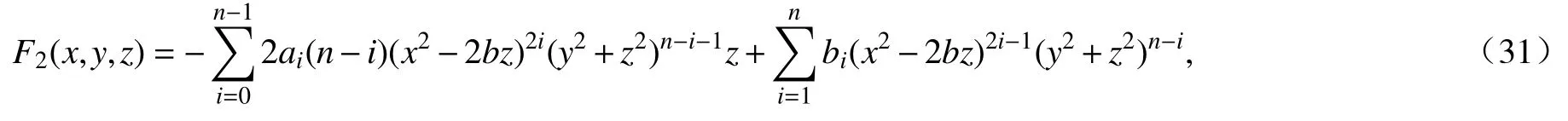
这里bi是实常数,其中i=0,1,···,n−1.同样地,由式(11),当j=3时,计算得
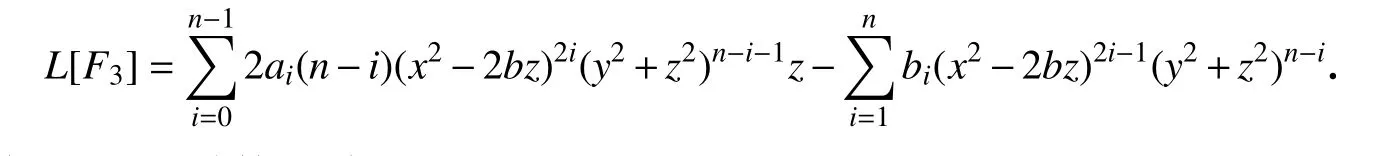
类似地,通过计算,我们得到
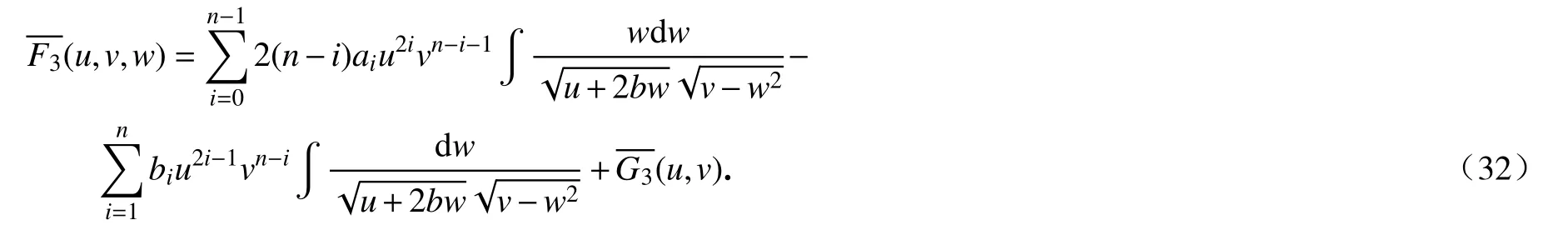
由于F3是权次为4n−3的权齐次多项式,则有(u,v)=0,且

这表明F2=0,F3=0.循环计算,当i=4,5,···,m时,我们可以得到Fi=0.由式(33)的第一个式子得到,对i=0,1,···,n−1,有ai=0.结合条件,存在i0∈0,1,···,n,使得ai0≠0.由此可得,系统(8)的Darboux 多项式为F=an(x2−2bz)2n,对应的余因子为−2n.回到系统(1),我们得到系统(1)的Darboux多项式为F=an(x2+2bz−2b)2n,对应的余因子为−2n.
条件(ⅱ) 当c≠1/2,k0=−2n,a0≠0,且对i=1,2,···,n,有ai=0 时,我们有F0=a0(y2+z2)n,F1=0.由式(11),当j=2 时,计算得

由于F2是权次为4n−2的权齐次多项式,则有
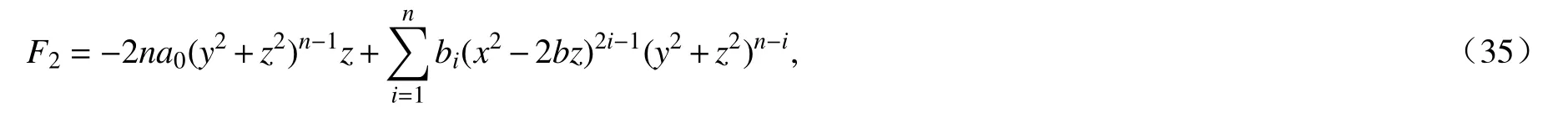
这里bi是实常数,其中i=0,1,···,n−1.接下来,由式(11),当j=3时,计算得
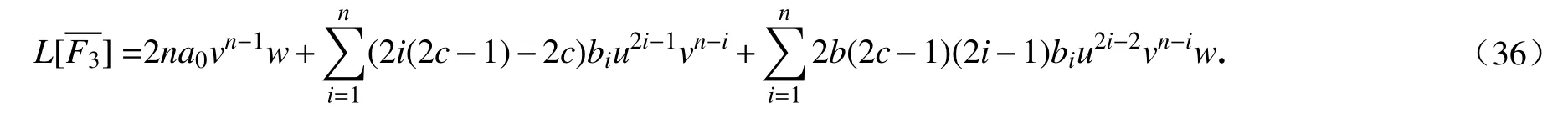
于是我们有
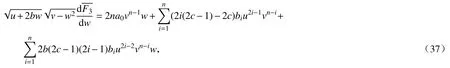
将方程(37)关于w求积分,得到

由于F3是权次为4n−3的权齐次多项式,则有(u,v)=0,且

这表明F3=0.因为a0≠0,c≠1/2,由式(39)的第一个式子知,b1≠0;由式(39)的第三个式子知bi=0,i=2,3,···,n,由式(39)的第二个式子,令i=1,有(c−1)b1=0,于是求得c=1,b1=−a0n/b.代入式(35),我们有
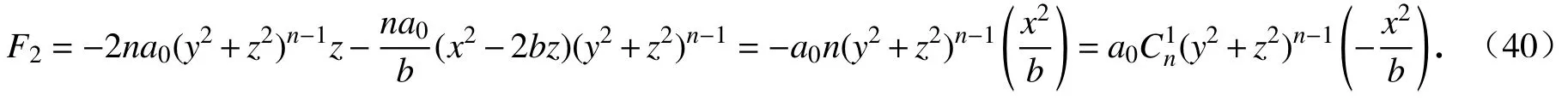
将F3代 入式(11),当j=4时,我们求得
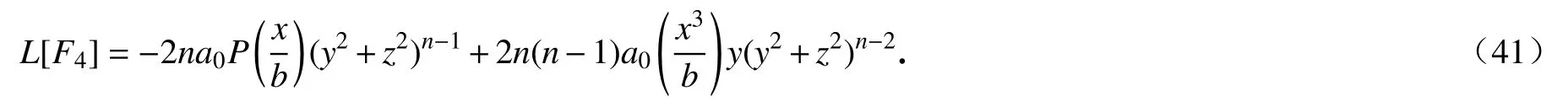
与F3类似的求解方法,我们求得
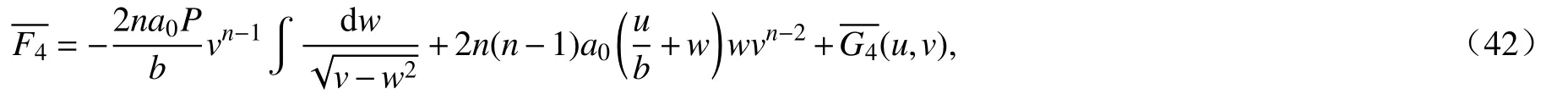
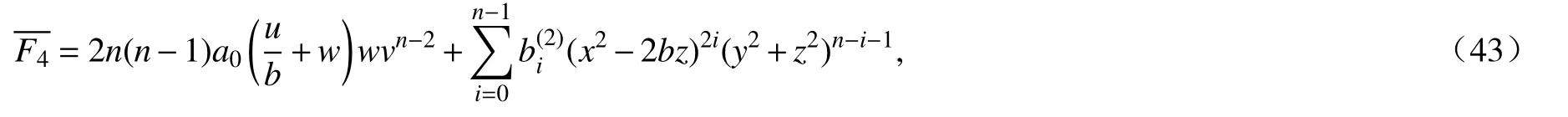
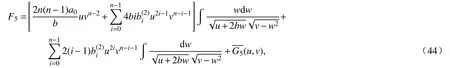
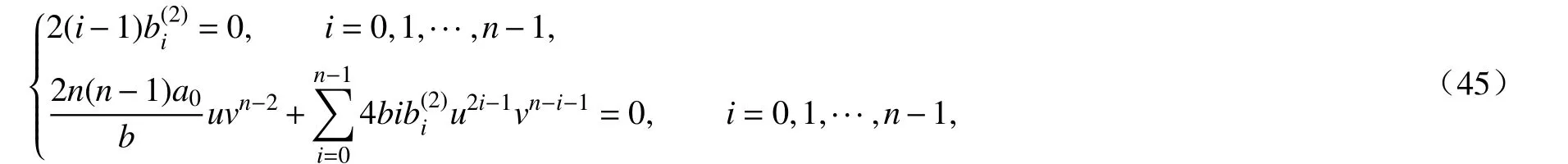
这表明F5=0.在式(45)的第二个式子中,令i=1,得到于是有


循环计算,我们得到
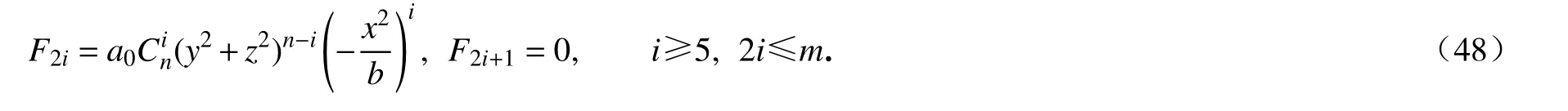
因此系统(8)的Darboux 多项式为

对应的余因子为−2n.回到系统(1),我们得到系统(1)的Darboux 多项式为对应的余因子为−2n.
2.2 F0的形式为式(21)
将F0代入式(11)的第二个方程,我们计算得到

与上一种情况计算方法相似,我们求出
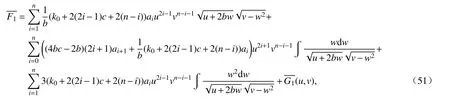
其中a0=an+1=0.进一步,条件(52)可以等同以下条件:
(ⅰ)c=1/2,k0=−2n+1,且存在i0∈1,2,···,n,使得ai0≠0;
(ⅱ)c≠1/2,F0=0.
这里对两个条件进行说明.我们首先假设2c−1=0,于是条件(52)可以被简化为

若k0−1+2n≠0,则对i=1,2,···,n,必须有ai=0,此时F0=0,Darboux 多项式不存在.若k0−1+2n=0,则须存在i0∈1,2,···,n,使得ai0≠0,否则F0=0,即为条件(ⅰ).现在假设2c−1≠0,于是由a0=an+1=0和条件(52)的第一个式子,可以看出,对i=1,2,···,n,有ai=0,则有F0=0,即为条件(ⅱ).显而易见,当F0=0时,系统(8)不存在Darboux 多项式,所以对条件情况(ⅱ)不再进行分析.现在我们计算系统(10)在条件(ⅰ)下的Darboux 多项式.
当c=1/2,k0=−2n+1,且存在i0∈1,2,···,n,使得ai0≠0时,有F1=0.由式(11),当j=2时,计算得
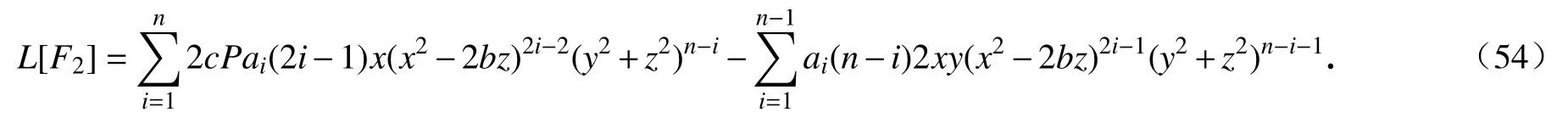
按照之前类似的计算,我们能够得到
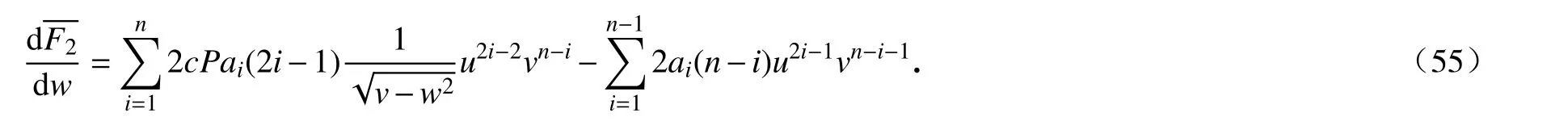
将式(55)关于w求积分,得到
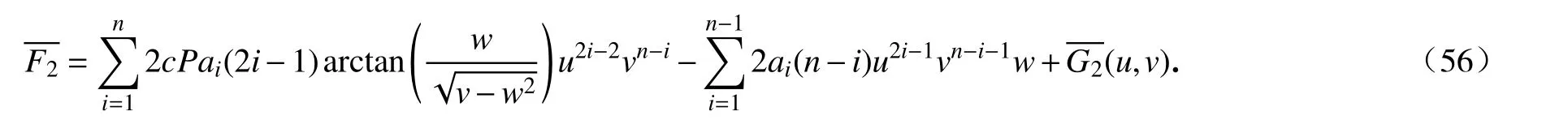
由于F2是权次为4n−4的权齐次多项式,则有

由于存在i0∈1,2,···,n,使得ai0≠0,且c=1/2,则P=0.于是F2可写为

这里bi是实常数,其中i=0,1,···,n−1.接下来,由式(11),当j=3时,计算得
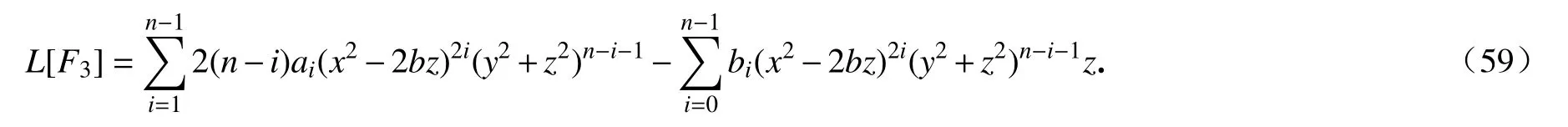
类似地,我们得到常微分方程(对于固定的u,v):
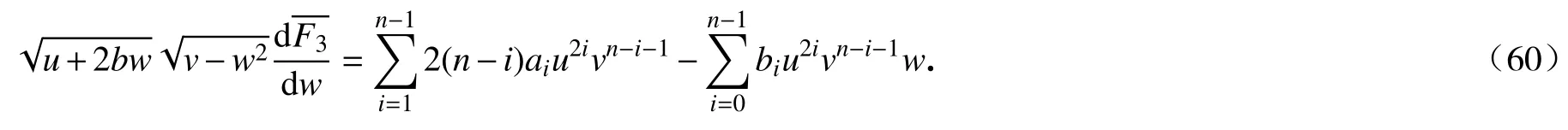
将方程(60)关于w求积分,得到
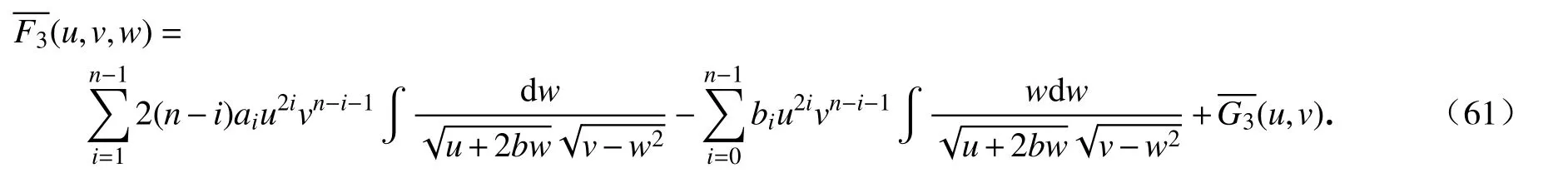
由于F3是权数为4n−5的权齐次多项式,则有G3(u,v)=0,并且有

这表明F3=0,且对i=1,2,···,n−1,有ai=0,对i=0,1,···,n−1,有bi=0.此时F2=0.循环计算,可以得到Fi=0,i=4,5,···,n.根据条件(ⅰ),存在i0∈1,2,···,n,使得ai0≠0,于是有an≠0,因此系统(8)的Darboux 多项式为F=an(x2−2bz)2n−1,余因子为−2n+1.回到系统(1),我们得到系统(1)的Darboux 多项式为F=an(x2+2bz−2b)2n−1,对应的余因子为−2n+1.
定理1 证毕.
3 结 论
基于加权齐次多项式和特征曲线的方法,通过求解线性偏微分方程,研究了Vallis 系统的Darboux 多项式和不变代数曲面问题.最终,在适当的参数条件下,我们得到了Vallis 系统的三类Darboux 多项式.除了Darboux 多项式和不变代数曲面问题,Vallis 系统的首次积分和代数可积性等问题也值得思考.

