一类热弹性板的空间衰减估计*
石金诚
(广州华商学院 数据科学学院,广州 511300)
引 言
1856年,Saint Venant 提出了一个著名的数学和力学上的具有广泛应用的原理,称之为Saint-Venant 原则.随后应用数学与力学领域中掀起了对该原则的广泛研究.早期对Saint-Venant 原则的研究主要集中在椭圆型方程的初边值问题上.Boley[1]将Saint-Venant 原则的研究推广到抛物方程上来,这些研究的目的是为了得到方程或者方程组的解类似于椭圆方程的Saint-Venant 原则(见文献[2]).Knowles[3]在研究平面弹性静力学中的Saint-Venant 原则时,建立了双调和方程解的空间指数衰减估计.后来,Payne 和Schaefer[4]得到了双调和方程在三个不同区域的Phragmén-Lindelöf 二择一结果.文献[5-7]利用各种方法研究了双调和方程的空间性态.对于与时间相关的双调和方程解的性态研究可见Liu 和Lin[8]的研究,他们采用二阶微分不等式的方法得到与时间相关的Stokes 方程的Phragmén-Lindelöf 二择一结果.上述文献所考虑的方程均是单个方程,由于双调和方程研究的难度较大,导致研究双调和方程组的文献较少.
近年来,国内也有一些学者开始进行解的空间衰减估计或Phragmén-Lindelöf 二择一的研究,文献[9-15]得到一些抛物方程解的空间性质.本文尝试研究双曲抛物耦合方程组的空间衰减估计.由于方程组中两个方程的性态不同,从而加大了构造能量表达式的难度.本文安排如下:首先,在第1 节提出我们所要研究的问题;然后,在第2 节中推导出解的能量表达式;接着在第3 节中利用微分不等式技术得到了解的空间衰减估计;最后,给出一些具体应用,得到了一些解的点点衰减估计的结果.由于方程组是双曲抛物耦合系统,如何构造合适的能量表达式是本文的最大创新,如何控制能量表达式是本文最大的难点.本文中采取以下符号约定,用逗号表示求偏导,用,i表示对xi求 偏导(i=1,2),如:v,i表示∂v/∂xi,重复的希腊字母α,β表示1 至2 求和,如:

1 准备知识
我们在如下无界区域 Ω0内考虑:

其中h是一给定的大于零的常数.同时引入下面的记号:

文献[16]中研究了著名的α-β模型,通过Fourier 变换的方法,得到了一些解的时间性态结果.本文中继续讨论此类问题,研究其解的空间性质.我们所考虑的是σ=2,α=1/2时的方程组(见文献[16]中式(6.2)):

其中u表示板的垂直扰度,v表示温度差,Δ表示Laplace 算子,Δ2表示双调和算子.上述模型可以用来描述由弹性膜和弹性板构成的演化过程.方程(3)和(4)满足如下初边值条件:

gi(x2,t),i=1,2,3是给定的函数并满足如下的相容性条件:

此外,解在无穷远处添加如下限制条件:

本文中,我们尝试得到双调和方程组 (3)、(4)的解在条件(5)~(7)下的空间衰减估计.
2 能量表达式 φ(z,t)
为了得到本文的主要结果,首先需要推导出能量表达式.
在式(3)两边同时乘以exp(−ωη)(ξ−z)u,η并积分,可得

定义函数φ1(z,t)如下:

联合式(8)和(9),可得

在式(4)两边同时乘以exp(−ωη)(ξ−z)v并积分,可得

定义函数φ2(z,t)如下:

联合式(11)和(12),可得
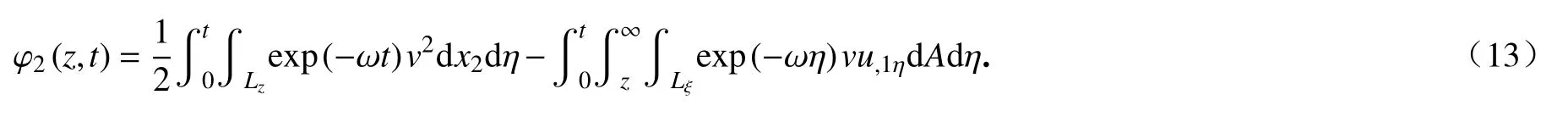
定义一个新的能量函数:

联合式(9)、(12)和(14),可得

联合式(10)、(13)和(14),可得
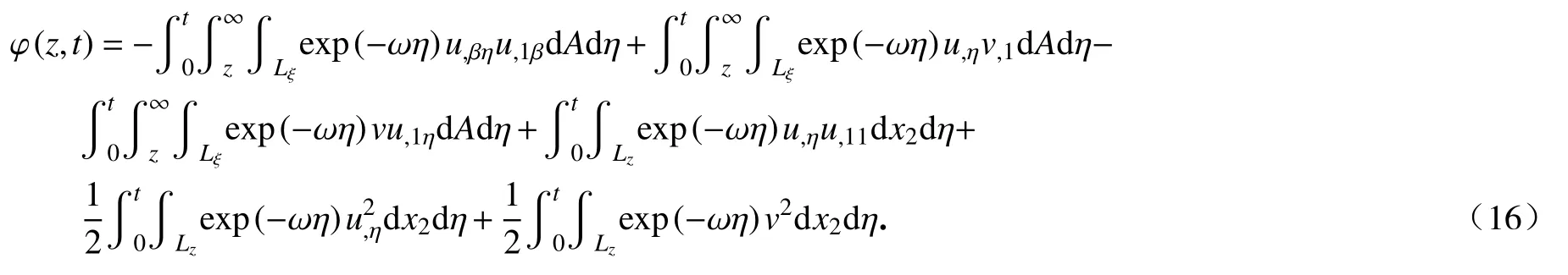
接下来我们需要根据φ(z,t)的性质推出所需的结果.
3 空间衰减估计
这一节我们将得到如下的空间衰减估计.
定理1假设(v,θ)为初边值问题(3)~(6)的经典解,则对于能量表达式E(z,t)与φ(z,t)有如下估计:

其中E(z,t)是大于零的函数,k6是大于零的常数.
证明式(15)两边同时对z求偏导,可得
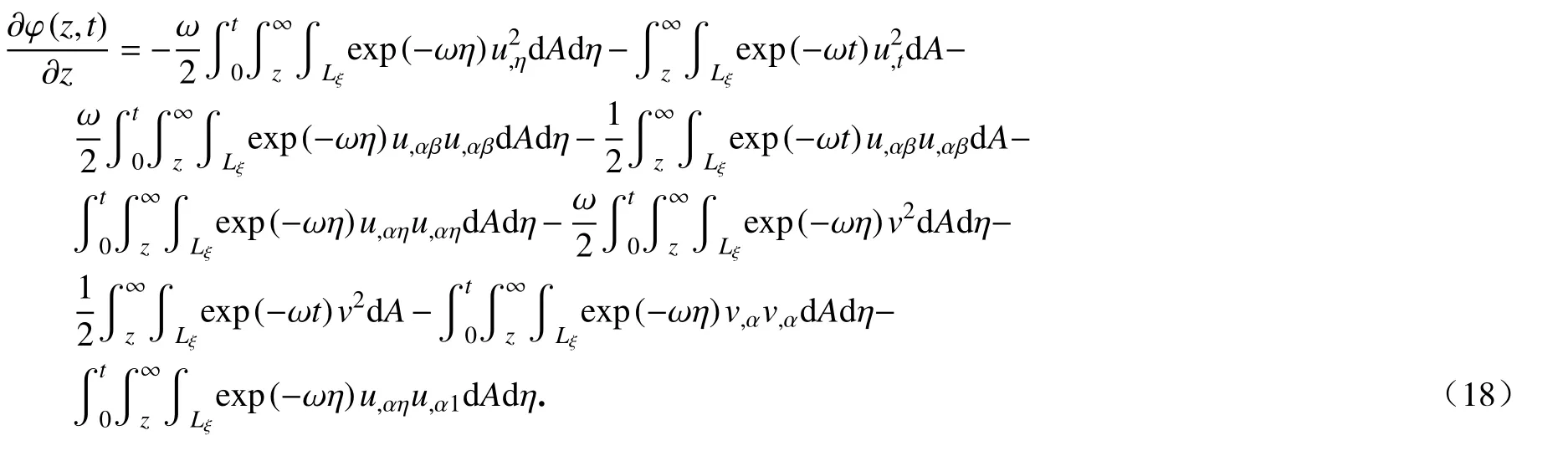
运用Schwarz 不等式,可知

将式(19)代入式(18),可得
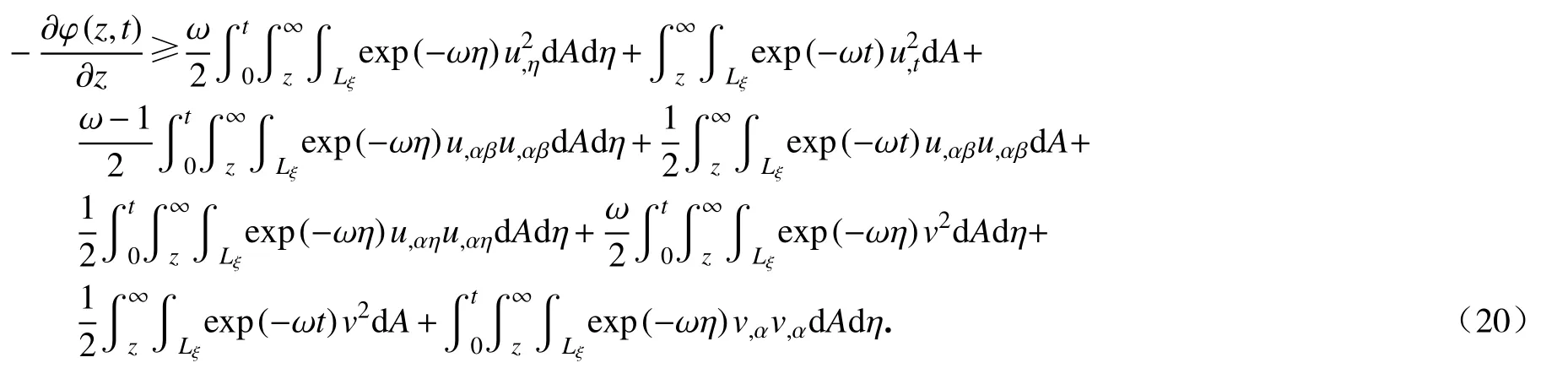
由式(18),可得

类似于式(20),同样可得

下面我们将给出式(16)的估计,运用Schwarz 不等式,可知

其中k1=max{2/(ω−1),2},ω是大于1的任意常数.
式(16)剩余的项可如下估计:

联合式(16)、(23)和(24),可得

令k3=k1/k2,k4=1/k2,则式(25)可变形为

不等式(26)可写为

由式(27),可得

对式(28)两边同时从z到 ∞上积分,可得

求解式(29),可得

其中φ (0,t)可以通过初始数据来控制,本文省略其估计过程.
类似于式(20)的推导过程,由式(15)可得

联合式(30)和(31),可得

式(32)即是我们所需证明的空间衰减估计结果.
4 应 用
在定理1的基础上,可得到一些点点衰减估计的结果.下面的这些结果是双调和方程所特有的.
引理1在定理1的基础上,有如下的不等式成立:
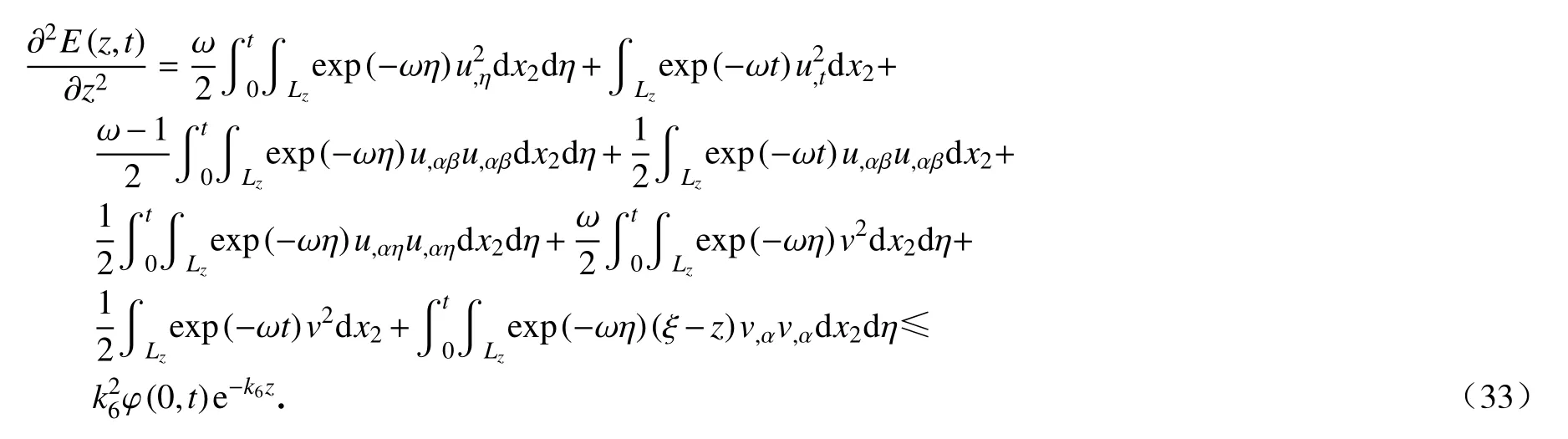
证明联合式(31)和(17),并运用两次L’Hospital 准则即可得到式(33).
引理2[3]若u(x2)∈c2[0,h],u(0)=u(h)=u,2(0)=u,2(h),则

定理2在定理1 式(17)指数衰减的基础上,对于u有如下点点衰减估计:

证明显然有

对式(38),由Schwarz 不等式,可得

联合式(34)、(35)和(39),可得

联合式(33)和(40),可得

同样易得

对式(42),由Schwarz 不等式,可得

联合式(34)和(43),可得

联合式(33)和(44),可得

式(41)和(45)即是我们所需证明的结果.
5 结 论
本文考虑了定义在二维半无限带形区域上热传导方程组解的空间衰减估计,得到了解的能量函数随着距离趋于无限远端呈指数衰减.采用文中的方法同样可以得到其他热传导方程组解的空间衰减估计,同时这类研究还可以向三维空间上的非线性方程组展开,据笔者所知,目前这类文献还较少,三维空间上的非线性方程组解的空间渐进性态是我们接下来考虑的一个方向.
致谢本文作者衷心感谢广州华商学院校内导师制项目(2020HSDS16)对本文的资助.

