压电超材料梁中弹性波带隙特性与界面传输的主动控制*
孙文静,王毅泽
(1.北京交通大学 土木建筑工程学院 力学系,北京 100044;2.天津大学 机械工程学院 力学系,天津 300350)
引 言
声子晶体和弹性波超材料是由两种或两种以上弹性材料周期性排列构成的新型功能结构.由于结构周期性,弹性波和振动在带隙的频率范围内不能在结构中传播[1-7].声子晶体和弹性波超材料可以提供许多新领域的应用,如滤波、隐身、聚焦等.其中关于直线型结构的研究包括,低阶Lamb 波在周期板中的传播[8]、考虑热效应的无序层状声子晶体中的弹性波局部化[9],以及周期性压电耦合梁中的波传播和带隙特性[10]等内容.
声子晶体和弹性波超材料通常表现为有序对称的周期性结构.随着周期特点的变化,带隙的位置和宽度将随之改变,有时甚至会产生新的带隙[11].这为研究设计特殊形式的弹性波超材料提供了新的思路,如已报道了具有交错层状和三明治层状结构的周期性板结构[12-13].当填充率或者几何参数发生变化时,带隙的特性会随之改变.因此,可以通过设计周期结构来调控弹性波的传播特性.然而,以往的研究通常局限于改变弹性波超材料的几何结构与组成材料的参数,因此上述结构一旦加工成型便不便于调节带隙行为,从而使得控制方法不够灵活.
另一方面,由于力电耦合效应,压电材料能够方便地改变材料参数[14-17].可以采用压电材料以及主动控制系统,实现对弹性波传输的主动控制[18-24],从而改进以往被动调节方式灵活性不足的缺点.本文研究了主动控制对弹性波超材料梁中带隙特性的影响,采用与压电片连接的负电容电路进行调控,从而改变带隙与界面传输特性.本文基于传递矩阵和Lyapunov 指数方法,给出了弹性波的带隙特性,通过有限元计算和实验证明了理论结果的正确性.
1 基本方程和理论推导
将压电片与外部负电容电路连接,然后周期性地黏附在基体梁结构上,用以调控周期结构中弹性波的传播特性,如图1所示.类比于固体物理学中的晶体结构形式,可以将含有压电分流电路的复合结构看作一个单胞,在空间上周期性排布,形成一种特殊的晶格结构.这种单胞主要包含三部分,即基体结构、压电片和外部电路.其中,外部分流电路和压电片共同作用可以主动控制超材料中的弹性波传输特性.图2给出了本文考虑的弹性波超材料梁结构,该结构由相同单胞周期排列构成.选取树脂材料作为基体梁,在其上下表面周期性地粘贴压电陶瓷片,每个单胞的厚度为h=hb+hpt+hpb,其中hb是基体梁的厚度,hpt和hpb分别是上下层黏附的压电片厚度.
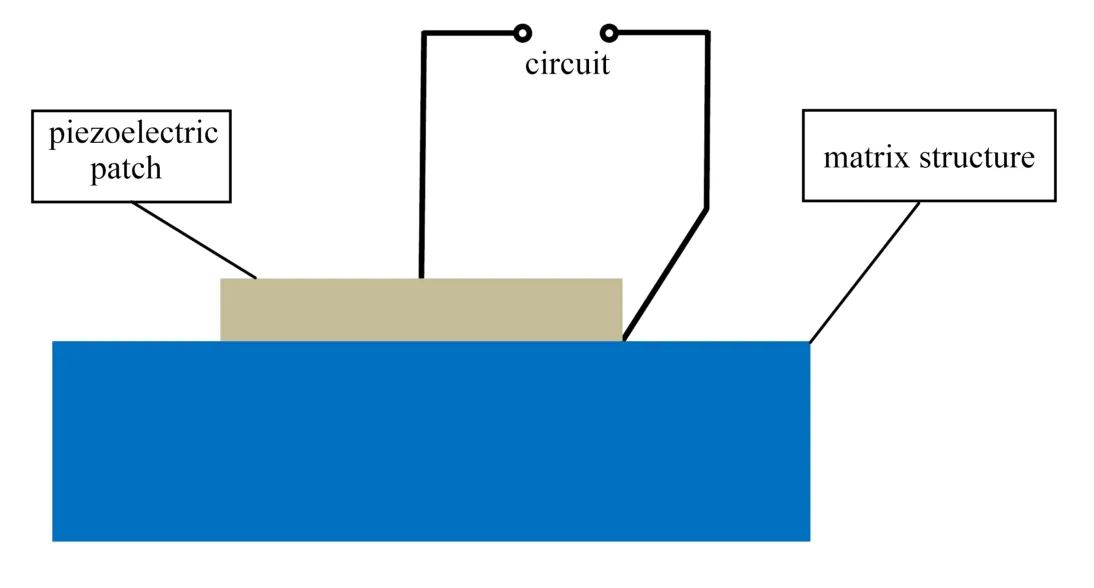
图1 压电分流结构单胞Fig.1 The unit cell of the piezoelectric circuit
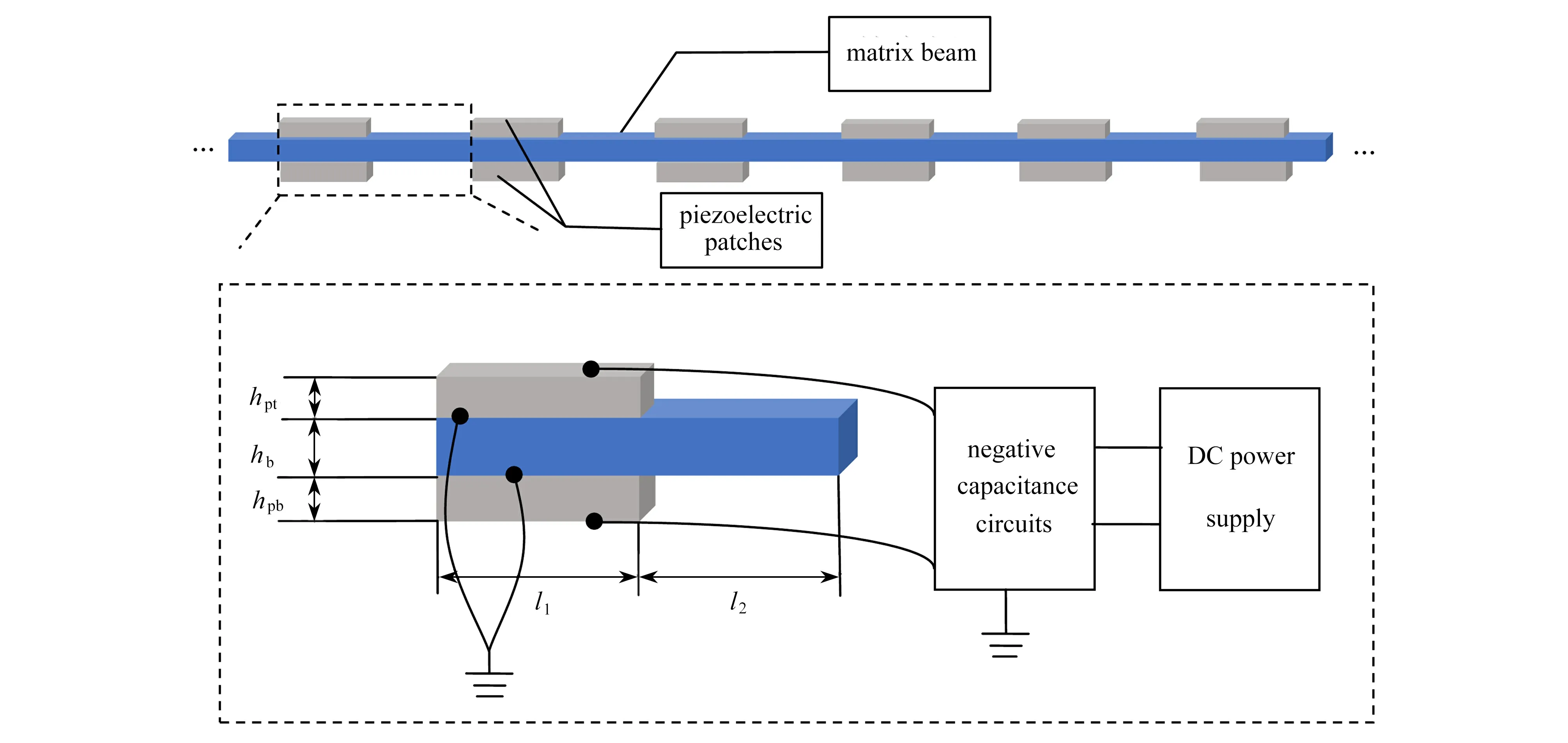
图2 具有不等厚度压电片的主动弹性波超材料梁Fig.2 Active elastic wave metamaterial beam attached by piezoelectric patches with different thicknesses
压电材料的本构方程为[21]

其中,下标1 和3 分别表示x和z方向,S1和T1分别表示沿x方向的应变和应力,是压电材料的柔度系数,d31和分别表示压电常数和介电常数,D3和E3分别代表沿z方向的电位移和电场强度.
压电材料的本构关系可以表示为[22]

其中,Z是复阻抗,As是压电片的电极面积,Cp=εT33As/Hp是压电片的固有电容.
从而可以推导出压电片的弹性模量为

采用图3所示的负电容电路作为主动控制系统,其包含电容C和补偿电阻R0,运算放大器的型号为LM 324N,复阻抗可定义为
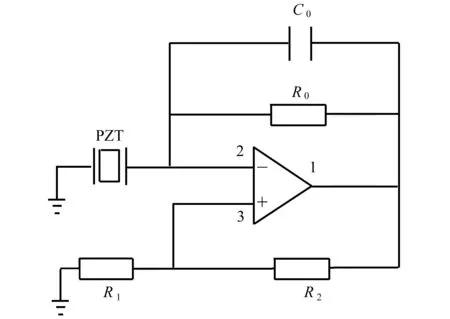
图3 含有负电容电路的主动控制系统Fig.3 The active control system with a negative capacitance circuit

其中,R1是固定电阻阻值,R2是滑动变阻器阻值.
选取图2单胞中的l1部分进行分析,其中不同厚度的压电片hpt和hpb分别贴附在梁的上下表面,图4给出了该部分的变形情况.假设压电片和基体梁具有相同的旋转角度.由于结构厚度较小,此时两部分中性层位置差别可以忽略[10,18].因此,基体梁和上下层压电片中性层的轴向位移分别为u1b,u1pt和u1pb,它们之间的相互关系可以表述为

图4 变形关系:(a)超材料梁的变形;(b)节点的位移Fig.4 The deformation relation:(a) the deformation of the layered elastic-piezoelectric beam;(b) the displacements of the nodes

式中,θ1=∂w1/∂x是旋转角度.
另一方面,对于上下层压电片厚度不相等的情况,l1部分的应变能和动能可以分别表示为

式中,E为弹性模量,A为横截面积,I为惯性矩,ρ为每一层的质量密度,t为时间.
对于l2部分,只有基体梁而没有压电片,因此其应变能和动能可分别表示为

式中,u2b为基体梁的轴向位移,w2为横向位移,l2为该部分的长度.
根据式(5a)和(5b),可以用ub代替式(6a)和(6b)中的upt和upb,得到此时的位移变量.图4所示的梁位移矢量可表示为
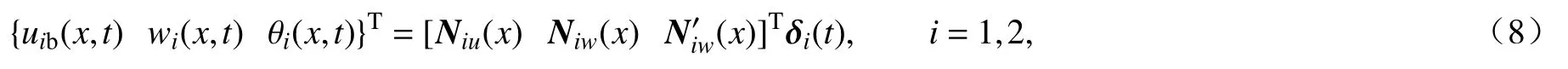
式中,i表示单胞的第i部分,Niu(x)和Niw(x)为形函数,δi(t)代表节点位移向量.
以上分量可以表达为


式中,L 和R 分别表示梁单元的左右两侧.
从而单胞的l1和l2部分可以推导为

式中,刚度矩阵和质量矩阵的表达式为

考虑以角频率为ω的弯曲波在超材料梁中传播,基于以上推导,动态刚度矩阵可以定义为

式中,Kdi代表单胞第i部分的动态刚度矩阵.
根据以往关于周期结构的研究[9,25],由传递矩阵可以得到局部化因子,从而得出带隙特性.在第j个单胞中,其第i部分的平衡方程为
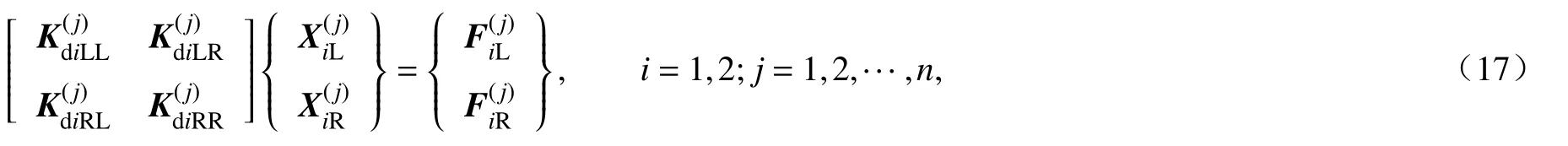
式中,KdiMN(M,N=L,R)是第j个单胞中Kdi的3×3 子矩阵,X(j)和F(j)是广义位移矢量和广义力矢量.
从而方程(14a)和(14b)可以推导为

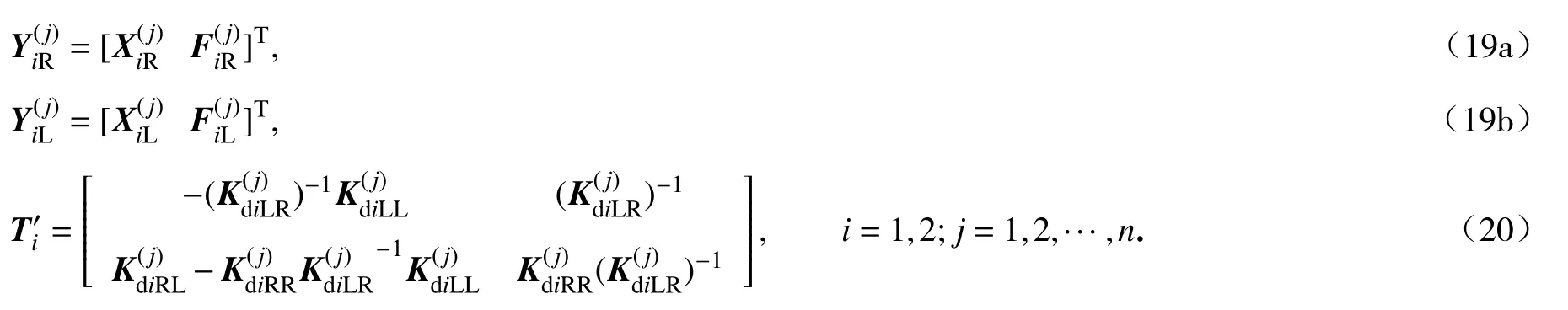
根据单胞相邻两个部分交接面处的相互关系,位移和力的状态矢量为

另一方面,相邻单胞交界面处的矢量可以写成

式中

所以第j个单胞中l1部分左侧和l2部分右侧之间的关系为

式中,T′是第j个单胞的传递矩阵,其表达式为

第j个单胞左侧状态矢量可以通过第j–1 个单胞右侧的状态矢量表示为

根据方程(24)和(26),第j–1 个单胞和第j个单胞的状态矢量满足如下关系:

其中,T(j)=T′J−1=T2′J−1T1′J−1是两个连续单胞之间的传递矩阵.
此外,本文利用了局部化因子表征带隙特性.Lyapunov 指数表征相对相空间相邻相轨线的平均指数发散或收敛程度,按数值大小排列最小正数的Lyapunov 指数即为其局部化因子.我们可以利用传递矩阵计算本系统的Lyapunov 指数以及局部化因子[9,25],局部化因子为零的区域对应能带结构中的通带,非零值区域则表示弹性波带隙,因此本文采用局部化因子描述带隙特性.
2 结果和讨论
本文从理论分析、有限元数值计算以及实验研究三个方面进行了讨论,研究此类结构的带隙和界面态传输性质.我们将着重讨论上下压电片厚度不相等以及主动控制的影响.本文采用压电片型号为PZT-5H,弹性模量为77.5 GPa,密度为7 500 kg/m3;基体梁为树脂材料,弹性模量为1.43 GPa,密度为1 200 kg/m3.当压电片在梁上对称粘贴时,改变压电片厚度并保持上下层厚度相同,其局部化因子变化情况如图5所示.从中可以看出,当压电片厚度由0.001 m 增大为0.001 2 m 时,结构中第一带隙频率范围由138~1 535 Hz 变为138~1 750 Hz,带隙起始频率不变,但宽度增加;第二带隙起始频率由2 641 Hz 变为2 963 Hz,但宽度几乎不变;而第三个带隙的起始频率明显变高,从6 740 Hz 变为7 477 Hz,变化幅度为737 Hz.
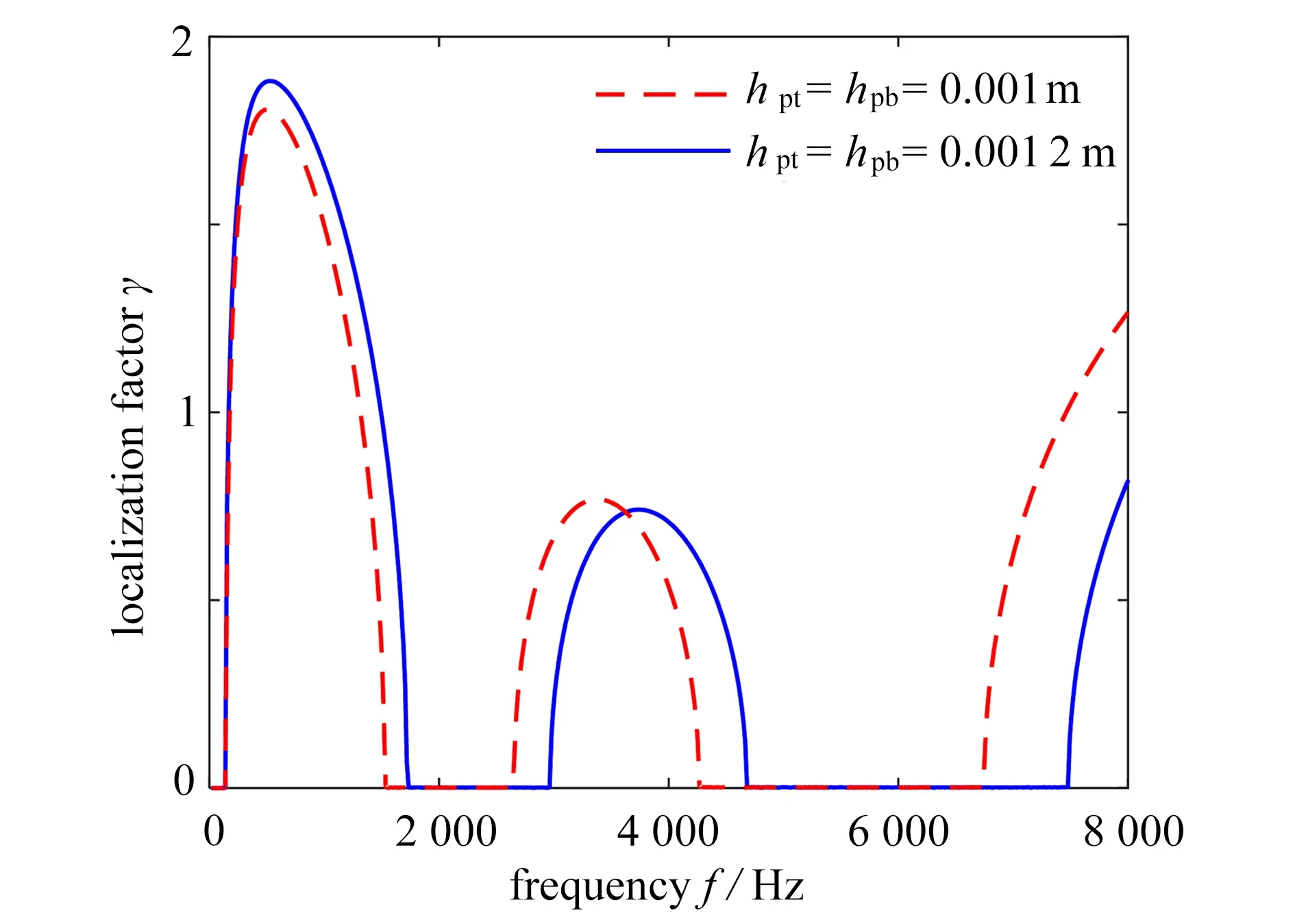
图5 压电片对称粘贴但厚度改变时弹性波超材料梁的局部化因子Fig.5 The localization factors of the elastic metamaterial beam with different-thickness piezoelectric sheets symmetrically pasted
当上下层压电片厚度相同与不同时,该弹性波超材料的局部化因子如图6所示.从图中可以看出,对于压电片厚度不等情况,第二带隙的位置存在明显的偏移,因此可以通过采用上下压电片不同厚度的方式调节带隙位置.另外,三个带隙的起始频率分别由138 Hz,2 641 Hz,6 740 Hz 变为1 520 Hz,2 794 Hz,7 124 Hz,均有不同程度的增大.
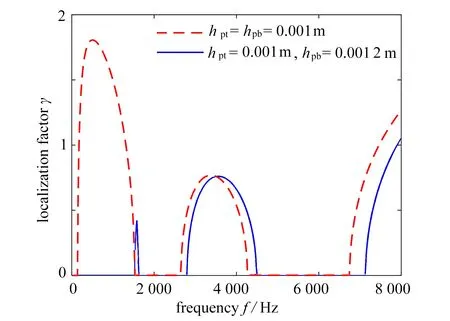
图6 上下层压电片厚度相同与不同时弹性波超材料梁的局部化因子Fig.6 The localization factors of the elastic metamaterial beam with the same- and different-thickness piezoelectric patches
图7给出了压电片厚度不相等时弹性波超材料梁中有无主动控制的局部化因子情况.主动控制系统通过改变压电片的弹性模量从而改变带隙特性.施加主动控制后,压电片弹性模量增大为156.6 GPa.从图中可以看出,进行主动调控之后,第一带隙的宽度明显变大,由1 520~1 627 Hz 变为1 520 ~2 303 Hz,其起始频率并未改变;第二带隙由2 794~4 499 Hz 变为3 961~6 372 Hz,起始频率变高,且变化十分明显,同时其宽度也相应变大.但在8 000 Hz 以下,主动控制后的能带结构中带隙的数量减少,只存在2 个带隙.
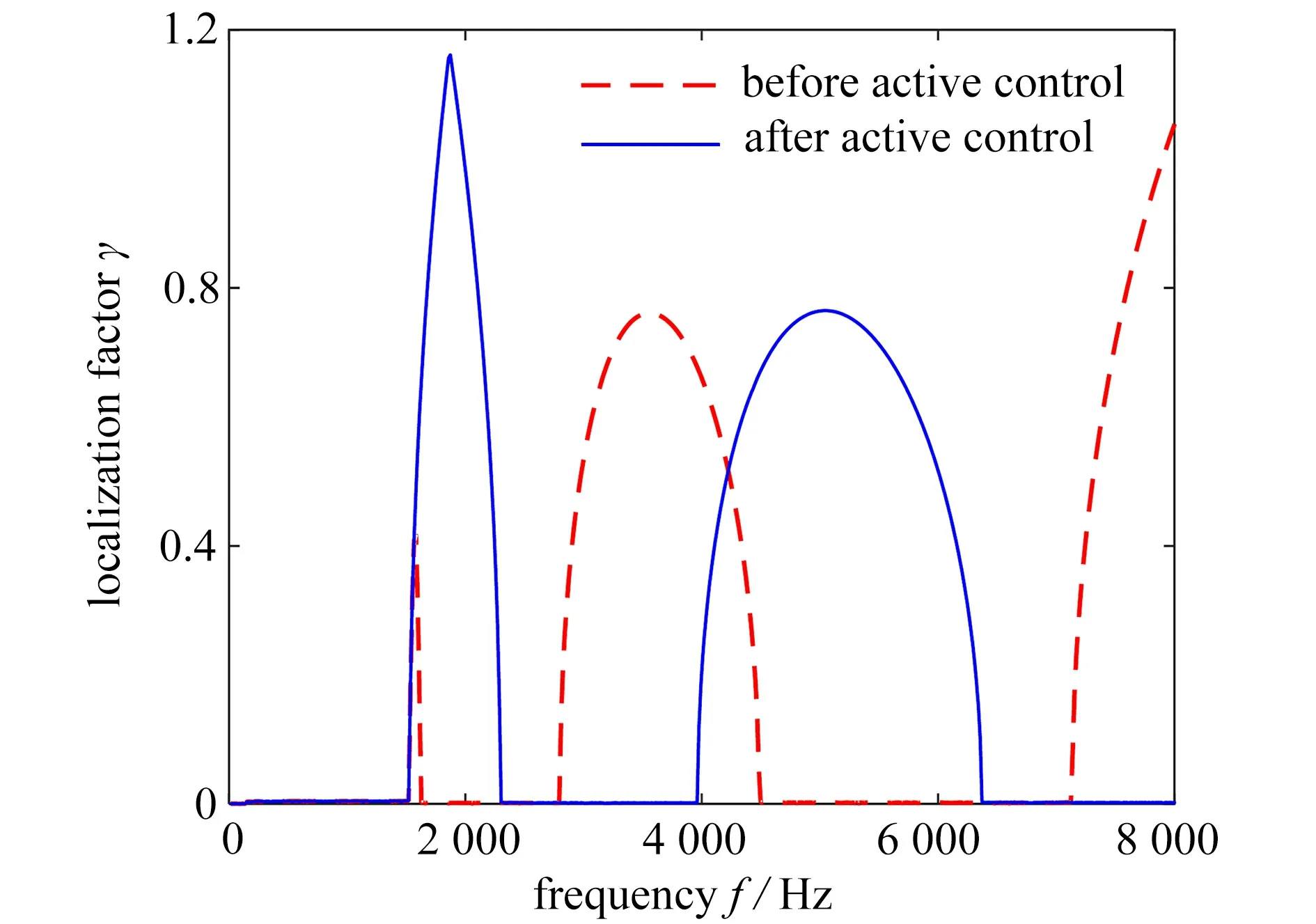
图7 弹性波超材料梁有无主动控制时的局部化因子Fig.7 The localization factors of the elastic metamaterial beam with and without active control
为验证主动控制系统的有效性,我们利用有限元软件COMSOL 对弹性波超材料梁的波动响应进行数值模拟,并且在上述分析的基础上开展了实验研究,图8为搭建的实验系统、实验模型以及相应的控制电路.在有限元数值计算中,我们选取了由7 个单胞周期排列而构成的弹性波超材料梁,在3 850 Hz 和5 659 Hz 两个频率点进行实验观测.从图7可以看出,3 850 Hz 处于带隙位置,弯曲波将不能在梁中进行传播.然而当施加主动控制之后,带隙位置发生改变,使得上述频率处于通带,从而弯曲波将可以传播.

图8 实验装置:(a)数据采集仪(上)和信号放大器(下);(b)信号发生器;(c)实验模型;(d)电路实物图;(e)压电片细节图Fig.8 The experimental equipment:(a) the data acquisition instrument (upper) and the signal amplifier (lower);(b) the signal generator;(c) the experimental model;(d) the physical circuit diagram;(e) the detailed diagram of the piezoelectric patch
同样在5 659 Hz 处有相反的现象发生,原本处于通带的弯曲波将由于处于禁带而不能传播.我们在实验模型的左端施加激励,在超材料梁的右端用传感器拾取响应.观察响应值与激励值,以此结果作为判断通带和带隙的依据.图9是用有限元软件COMSOL 计算得到的响应图,从图中可以明显发现,在3 850 Hz 处,弯曲波几乎没有传播.但是经过主动控制之后,弹性波的传播效果明显增强.在5 659 Hz 处,原本弹性波的传输效果较好,但经过主动调控后,弹性波传输衰减明显,几乎不能传播.
不同频率的实验结果如图10所示,可以观察到与图9一致的结论.图10给出的是激励端和接收端时域信号经过Fourier 变换之后的响应值,其中虚线代表激励信号,实线代表接收信号.从图中可以观察到,在3 850 Hz 处,弹性波在主动控制前的接收信号强度约为30%,但经过主动调控后,接收信号强度增大为约82%.在5 659 Hz 处,主动控制前后的接收信号强度大约从80%下降至27%.上述理论分析以及数值计算的结论相一致,证实了主动控制系统的有效性.

图9 传输响应:(a) 3 850 Hz,主动控制前;(b) 3 850 Hz,主动控制后;(c) 5 659 Hz,主动控制前;(d) 5 659 Hz,主动控制后Fig.9 Transmission responses:(a) at 3 850 Hz before active control (b) at 3 850 Hz after active control;(c) at 5 659 Hz before active control;(d) at 5 659 Hz after active control
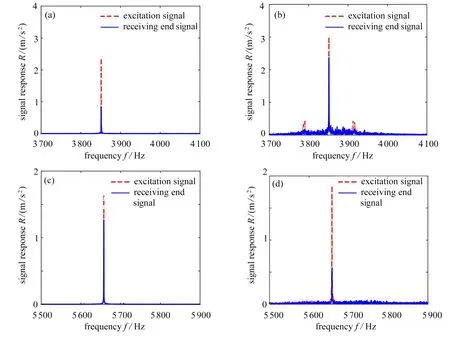
图10 激励端和接收端的响应值:(a) 3 850 Hz,主动控制前;(b) 3 850 Hz,主动控制后;(c) 5 659 Hz,主动控制前;(d) 5 659 Hz,主动控制后Fig.10 The responses at the excitation and the receiving end:(a) at 3 850 Hz,before active control;(b) at 3 850 Hz,after active control;(c) at 5 659 Hz,before active control;(d) at 5 659 Hz,after active control
如图11所示,我们在利用有限元软件对单胞进行计算时,注意到l1从6 mm 增大到25 mm的过程中,能带结构中第二个带隙先消失再产生.当l1=6 mm 时,两条能带之间的宽度为78 Hz,随着l1的增大,带隙宽度逐渐减小,当l1=15 mm 时,带隙在575 Hz 处消失.然而l1继续增大时,带隙重新出现,并且宽度随着l1的增大而增大,当l1=25 mm 时,两条能带之间的宽度为186 Hz.

图11 结构能带图Fig.11 The band structure
我们对此现象进行研究,分别取具有7 个l1=6 mm 以及7 个l1=25 mm的周期梁,然后将两个部分组合成一个弹性波超材料梁结构.在整体结构的左侧施加激励,在右侧拾取响应值,得到结果如图12所示.从中可以发现,原本在516~668 Hz 频率段的带隙,却在585 Hz 处出现了一个峰值,该值与单胞能带结构中第二个带隙消失的频率575 Hz 误差为10 Hz.主要原因为计算单胞能带结构时采用周期性边界条件,单胞构成的梁假设为无限周期梁,而实际计算的含有交界面的梁为有限周期结构.对585 Hz 处的波动幅值响应图进行观察,如图13所示,发现在两部分的交界面处出现了界面局域态.
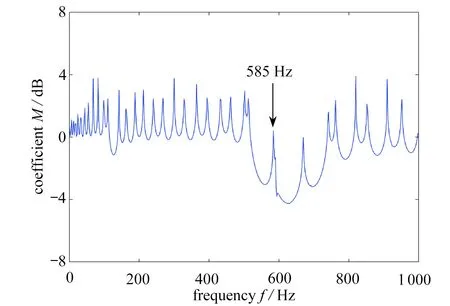
图12 响应图Fig.12 The response diagram

图13 弹性波幅值响应图Fig.13 The diagram of elastic wave responses
我们利用图8所示的实验系统,对上述分析结果进行了实验验证,图14为实验模型图.在梁的左端施加激励,用传感器在交界面处接收信号,将接收端的信号与激励端的信号进行Fourier 变换处理,得到结果如图15所示.从图中可以看出,经过主动控制之后,弹性波超材料梁中交界面处信号的响应较高.上述现象表明弹性波在结构中的传播发生了界面局域态的现象,与理论分析以及数值计算的结果一致.

图14 实验模型Fig.14 The experimental model
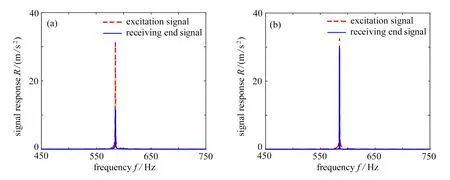
图15 激励端和接收端的响应值:(a)主动控制之前的实验结果;(b)经过主动调控之后的实验结果Fig.15 The responses at the excitation and the receiving end:(a) experimental results before active control; (b) experimental results after active control
3 结 论
本文研究了弯曲波在弹性波超材料梁中的传播问题,采用不等厚压电片周期性排布的方式,设计了含有负电容电路的主动控制系统,实现了弹性波带隙特性和界面态传输的主动控制功能.应用传递矩阵方法以及局部化因子计算了能带结构.研究结果表明,压电片厚度变化引起的填充率改变以及弹性模量均对弹性波的带隙特性存在影响.在此基础上,针对超材料梁的界面态传输进行了研究,发现了该超材料结构具有弹性波界面局域态的特殊性质.

